Matlab之信号分析
采集到一段信号,我们最想做的就是看信号的波形图以及信号的频谱图。波形图好画,但频谱图一直很难理解怎么画。而且自己采集到的一段信号可能是频率时变的,就需要窗函数截取信号,然后滑动查看信号频域变化。这种方法展示频域随时间的变化不太明显,就需要做时频分析,以期得到频域变化图。
1.产生特定频率的模拟信号
对于一个正弦波信号,可以写为如下的形式:
其中:
A是信号的振幅;
f 是信号的频率;
![]() 是信号的初始相位;
是信号的初始相位;
k 是信号的噪声电平;
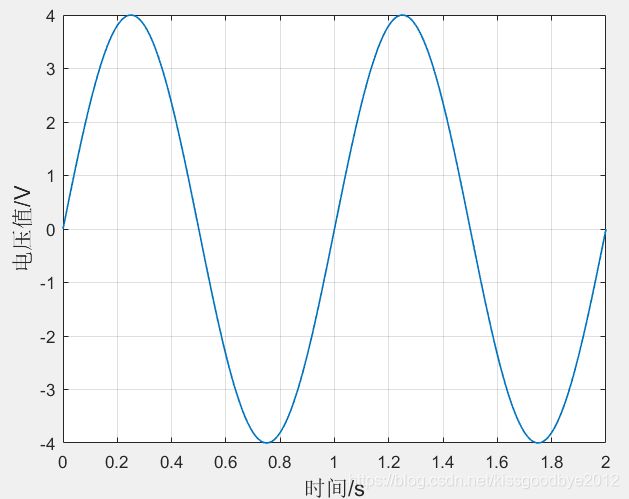
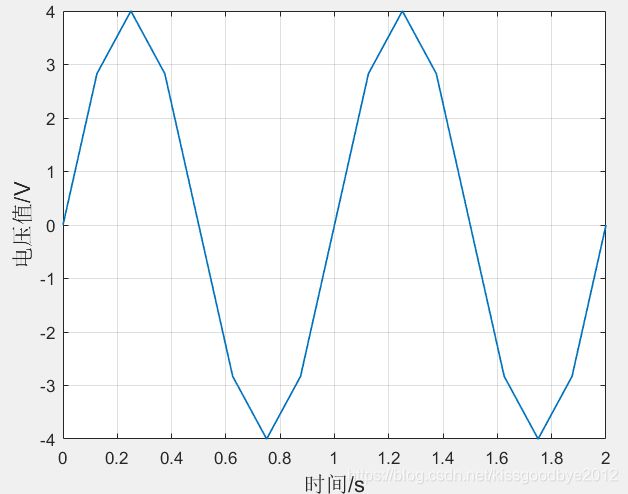
则,一个信号振幅为4V,频率为1Hz的电压信号可以绘制如下:
clc;clear;close all;
%% 参数初始化
A=4;%振幅
f=1;%频率
v=0;%初始相位
k=0;%噪声电平
fs=100;%采样频率
%% 画出波形
t = 0:1/fs:2;
x = A*sin(2*pi*f*t+v)+k;%弧度为单位
plot(t,x,'LineWidth',1)
grid on
xlabel('时间/s','FontSize',13);%设置x轴标签
ylabel('电压值/V','FontSize',13);%设置y轴标签
绘制结果如下:
2 采样定理
根据奈奎斯特采样定理(Nyquist-Shannon 采样定理):信号采样率fs必须大于被测信号感兴趣最高频率分量的两倍。通常希望采样率大于信号频率约五倍。
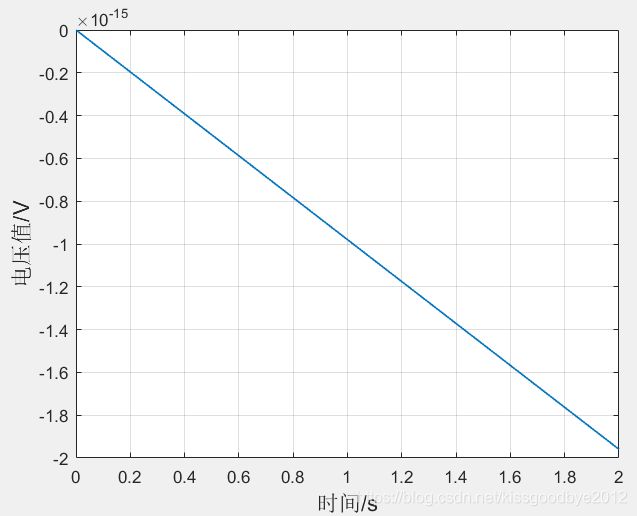
实验验证1:对于振幅是4V,频率为1Hz的信号,使用1Hz的采样率进行采样
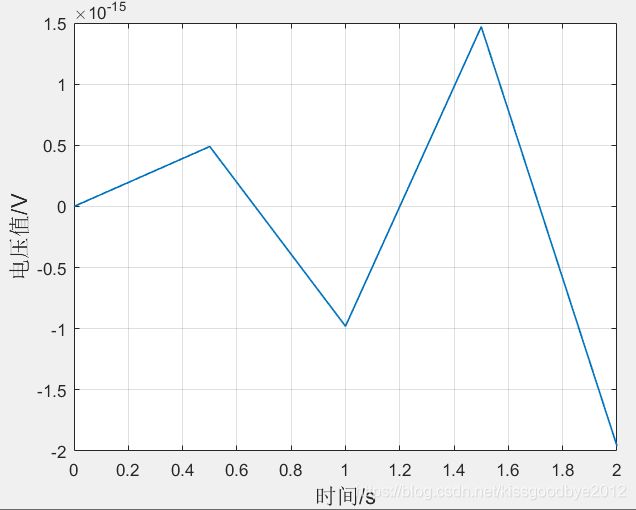
实验验证2:对于振幅是4V,频率为1Hz的信号,使用2Hz的采样率进行采样
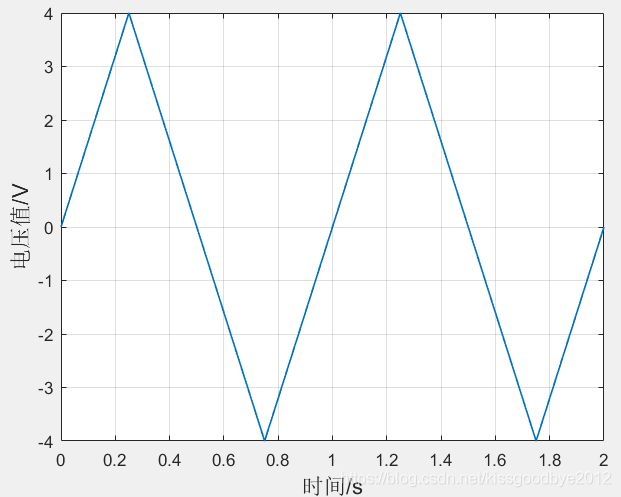
实验验证3:对于振幅是4V,频率为1Hz的信号,使用4Hz的采样率进行采样
实验验证4:对于振幅是4V,频率为1Hz的信号,使用8Hz的采样率进行采样
实验验证5:对于振幅是4V,频率为1Hz的信号,使用16Hz的采样率进行采样
结论:
从图中可以看出,随着采样率的提高,波形越来越趋近原始波形。当采样率只是信号频率的2倍时,其实信号畸变还是非常严重的,基本到4倍左右,才能基本看出波形周期和振幅。
3.FFT得到信号频谱图
参考文章链接:matlab进行傅里叶变换fft和shiftfft_Prozzz777的博客-CSDN博客_matlab 进行傅里叶变换
信号的频谱分析分为:实信号和复数信号的频谱分析。
实信号的频谱特点:关于原点对称,是双边谱。
复信号的频谱特点:只存在正频域部分,单边谱。
复信号是实际信号处理常用的表示形式:x=x_re+j*x_im;分为实部和虚部,虚部是实部的希尔伯特变换。
3.1 实信号的频谱分析
由于实信号是双边谱,因此可以看到信号的负频率。而进行了信号的时域采样,因此使得频域出现了周期性,周期为采样率。
使用fft得到只有正频域的,可以在正频率部分看到两根谱线(fft(x)运算后得到的是N的结果对应[0,fs]频点的对应的值,进行(abs(fft(x))*2/N)后才是对应的真是幅度值)。为了看到负频率部分的频谱,我们可以使用shiftfft函数,使用shiftfft时需要注意的是横坐标刻度是[-fs/2,fs/2]。
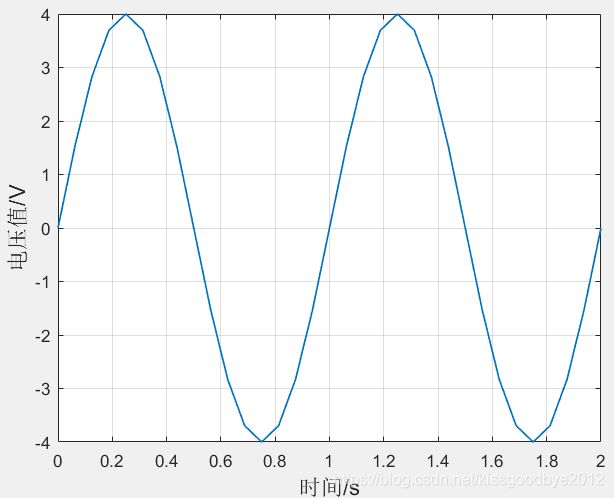
使用fft函数绘出实信号的频谱图:采样周期20Hz,由于周期性,19Hz的频点其实是负频率。
clc;clear;close all;
%% 参数初始化
A=4;%振幅
f=1;%频率
v=0;%初始相位
k=0;%噪声电平
fs=20;%采样频率
%% 画出波形
t = 1/fs:1/fs:2;
x = A*sin(2*pi*f*t+v)+k;%弧度为单位
plot(t,x,'LineWidth',1)
grid on
xlabel('时间/s','FontSize',13);%设置x轴标签
ylabel('电压值/V','FontSize',13);%设置y轴标签
%% 画出fft后的频谱图
N=length(x);
figure(2);
f1_index=(0:N-1)*(fs/N);
y1=abs(fft(x)).*2/N;
plot(f1_index,y1);
xlabel('频率(Hz)');ylabel('幅度(V)');绘制结果如下:这里要注意点数必须为偶数,不能是奇数,否则会出现频率误差。推荐的点数是2的幂次方,如1024等等。因为fft不足2的幂次方会补零,造成频率域扩宽。
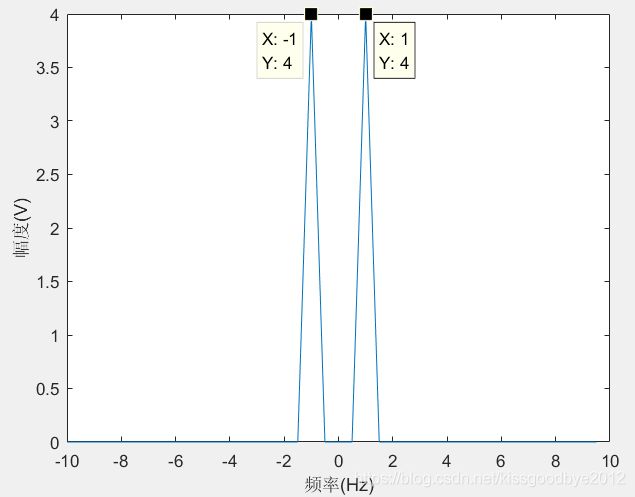
使用shiftfft绘制实信号的频谱图:采样周期20Hz
clc;clear;close all;
%% 参数初始化
A=4;%振幅
f=1;%频率
v=0;%初始相位
k=0;%噪声电平
fs=20;%采样频率
%% 画出波形
t = 1/fs:1/fs:2;
x = A*sin(2*pi*f*t+v)+k;%弧度为单位
plot(t,x,'LineWidth',1)
grid on
xlabel('时间/s','FontSize',13);%设置x轴标签
ylabel('电压值/V','FontSize',13);%设置y轴标签
%% 画出fft后的频谱图
N=length(x);
figure(2);
f2_index = (-N/2:(N-1)/2)*(fs/N);
y2=abs(fftshift(fft(x))).*2/N;
plot(f2_index,y2);
xlabel('频率(Hz)');ylabel('幅度(V)');绘制结果如下:
3.2 复信号的频域分析
4.绘制信号时频图
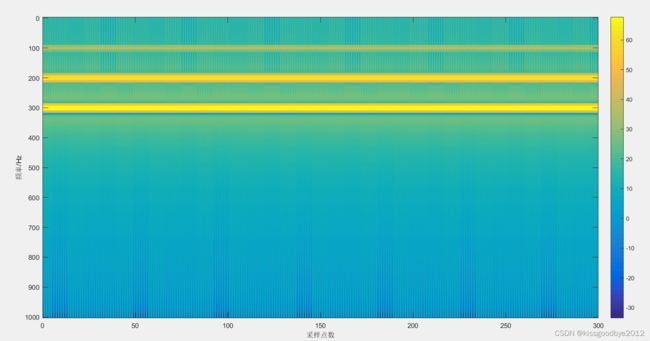
4.1 短时傅里叶变换法(STFT)
%% 短时傅里叶变换——求时频图
clc;clear;close all
%% 参数
Fs=2000;%采样率
%% 模拟数据
t=0:(1/Fs):300;
y1=sin(2*pi*100.*t);
y2=20*sin(2*pi*200.*t);
y3=40*sin(2*pi*300.*t);
y=y1+y2+y3;
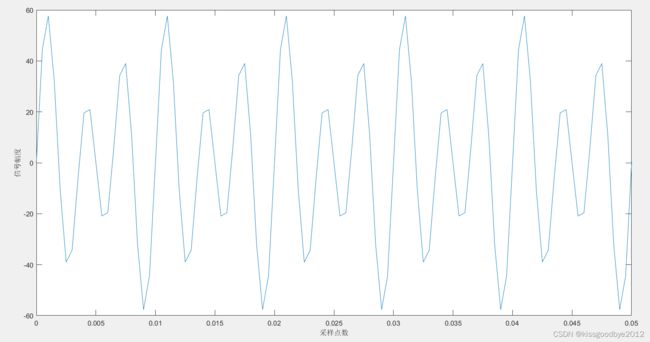
plot(t,y);
xlim([0,100/Fs])
xlabel('采样点数');ylabel('信号幅度');
%% 绘制时频图
%参数1:输入数据
%参数2:窗的宽度
%参数3:重叠部分宽度
%参数4:参与算法的总点数
%参数5:采样率
s=spectrogram(y,256,128,256,Fs);
f=linspace(0,Fs/2,size(s,2));
figure;
imagesc(t,f,20*log10((abs(s))));
xlabel('采样点数');ylabel('频率/Hz');
colorbar
4.2 小波变换法
参考文章:matlab时频分析之连续小波变换cwt
参考文章2:基于MATLAB短时傅里叶变换和小波变换的时频分析
%% 短时傅里叶变换——求时频图
clc;clear;close all
%% 参数
Fs=2000;%采样率
%% 模拟数据
t=0:(1/Fs):(3000/Fs);
y1=sin(2*pi*100.*t);
y2=20*sin(2*pi*200.*t);
y3=40*sin(2*pi*300.*t);
y=y1+y2+y3;
plot(t,y);
xlim([0,100/Fs])
xlabel('采样点数');ylabel('信号幅度');
%% 绘制时频图
%% matlab自带的小波变换
%新版本
figure(3)
[wt,f,coi] = cwt(y,'morse',Fs);
pcolor(t,f,abs(wt));
shading interp小波变换不带第三方库代码:
fs=2^6; %采样频率
dt=1/fs; %时间精度
timestart=-8;
timeend=8;
t=(0:(timeend-timestart)/dt-1)*dt+timestart;
L=length(t);
z=4*sin(2*pi*linspace(6,12,L).*t);
wavename='cmor1-3'; %可变参数,分别为cmor的
%定义计算范围和精度
fmin=2;
fmax=20;
df=0.1;
totalscal=(fmax-fmin)/df;
f=fmin:df:fmax-df;%预期的频率
wcf=centfrq(wavename); %小波的中心频率
scal=fs*wcf./f;
%自己实现的小波函数
coefs2=cwt_cmor(z,1,3,f,fs);
figure(3)
pcolor(t,f,abs(coefs2));shading interp
%后面是函数
function coefs=cwt_cmor(z,Fb,Fc,f,fs)
%1 小波的归一信号准备
z=z(:)';%强行变成y向量,避免前面出错
L=length(z);
%2 计算尺度
scal=fs*Fc./f;
%3计算小波
shuaijian=0.001;%取小波衰减长度为0.1%
tlow2low=sqrt(Fb*log(1/shuaijian));%单边cmor衰减至0.1%时的时间长度,参照cmor的表达式
%3小波的积分函数
iter=10;%小波函数的区间划分精度
xWAV=linspace(-tlow2low,tlow2low,2^iter);
stepWAV = xWAV(2)-xWAV(1);
val_WAV=cumsum(cmorwavf(-tlow2low,tlow2low,2^iter,Fb,Fc))*stepWAV;
%卷积前准备
xWAV = xWAV-xWAV(1);
xMaxWAV = xWAV(end);
coefs = zeros(length(scal),L);%预初设coefs
%4小波与信号的卷积
for k = 1:length(scal) %一个scal一行
a_SIG = scal(k); %a是这一行的尺度函数
j = 1+floor((0:a_SIG*xMaxWAV)/(a_SIG*stepWAV));
%j的最大值为是确定的,尺度越大,划分的越密。相当于把一个小波拉伸的越长。
if length(j)==1 , j = [1 1]; end
waveinscal = fliplr(val_WAV(j));%把积分值扩展到j区间,然后左右颠倒。f为当下尺度的积分小波函数
%5 最重要的一步 wkeep1取diff(wconv1(ySIG,f))里长度为lenSIG的中间一段
%conv(ySIG,f)卷积。
coefs(k,:) = -sqrt(a_SIG)*wkeep1(diff(conv2(z,waveinscal, 'full')),L);
%
end
end5.名词解释
5.1 负频率
关于负频率,目前的理解有两个,第一个看法是没有实际意义,可以看到,对信号进行傅里叶变换之后信号从实数域被转换到了复数域,而之所以会出现负频率,正是为了消除信号的虚部。实际上,傅里叶级数展开后,负频率对实部与对应正频率相同,而虚部相反从而消除虚部,从这个意义上来说,负频率没有实际的物理意义而纯粹是数学处理,另一个看法是负频率也可以存在,他可以理解为信号在复平面上的正转与反转,而负频率对应的正式反转。