【面试】数据结构+B树
目录
什么是数据结构？
数据结构有哪几种分类？
数组和链表在内存中的存储结构有什么区别？
说一下数据散列存储(Hash存储)结构？【查资料再归纳一哈】
如何解决hash冲突？
说说 数组，链表，循环，嵌套循环的时间复杂度
JDK中线性结构的集合有哪些？
什么是树【树的定义】？
你说一下树形结构和线性结构的优势？
说一下树的分类，以及你对它们的理解（二叉查找树的优缺点，平衡树的优缺点，红黑树的优缺点，B-树的优缺点 ，B+树的优缺点）平衡树 ，红黑树【还没有理解归纳成自己的知识】
二叉排序树【有序】
平衡二叉树【Balance Binary Tree】
红黑树【Red Black Tree】
HashMap为什么选择红黑树？
多叉树：
B树【Balance Tree】
B+树
有了二叉树为什么要出现多叉树？
b-tree和b+tree的区别？
说一下ES用到了什么数据结构？
Mysql为什么用B+Tree作为索引的存储结构
什么是数据结构？
数据结构就是用来存储有数据之间有一定关系的数据。比如采用数组，链表进行存储数据，都可以称为数据结构。
数据结构有哪几种分类？
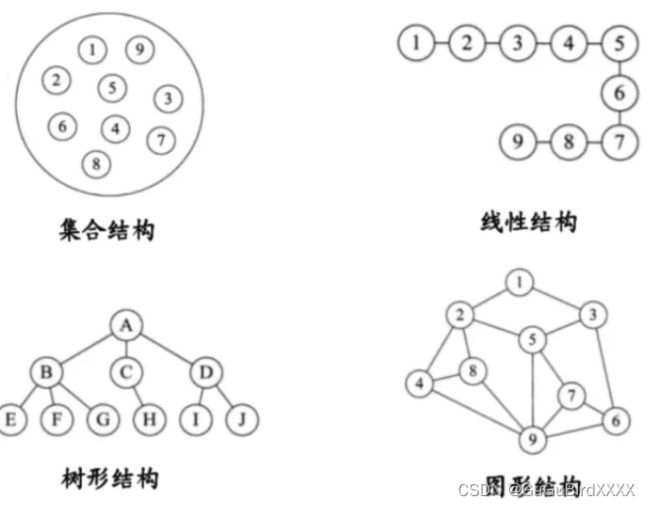
按照逻辑结构分
-
集合：没有相互关系的一堆数据
-
线性结构：元素存在一对一的相互关系
-
树形结构：元素存在一对多的相互关系
-
图形结构：元素存在多对多的相互关系
按照物理结构分
-
顺序存储结构：用一组地址连续的存储空间依次存储线性表的数据元素，也叫顺序存储结构，比如数组
-
链式存储结构：用一组任意的存储空间来存储线性表中的数据元素，不要求相邻元素在物理位置上也相邻，比如链表
-
数据索引存储结构：建立附加的索引来标识节点的地址，通过索引，可以很快检索数据【ES】
-
数据散列存储结构：将数据元素的存储位置与关键字之间建立确定的对应关系，加快查找的速度，又叫hash存储
数组和链表在内存中的存储结构有什么区别？
数组在内存中是一块连续的存储空间，它随机查改元素性能很高【通过下标get set】，但是增删操作，需要移动其他元素，因此性能很低
链表在内存中的存储空间可以是不连续的，而在每一个元素中都保存相邻节点的指针，因此查改的性能低，因为需要从第一个元素依次遍历，但是它的增删操作性能很高，因为它增删只需要改变相邻节点指针就行了，同时它更容易造成内存的碎片化？？？？【因为存储数据是不连续的，原本连续的存储空间被零散数据占用，而无法再分配大块连续的存储空间】
prev【Previous--前置节点】 next--后置节点
说一下数据散列存储(Hash存储)结构？【查资料再归纳一哈】
hashmap的put方法，对存储的数据进行hash算法计算出hash值，然后对数组长度进行（取模）位运算，然后进行存储，key就是经过位运算后计算的值，value就是存储的数据。
哈希冲突，也叫哈希碰撞，指的是两个不同的值，通过hash算法计算出了相同的hash值。
可以简单理解为：两个值都想存在同一个位置，就开始过捏（打架）。
如何解决hash冲突？
解决哈希冲突（四种方法）_君诀的博客-CSDN博客_解决哈希冲突的方法
-
拉链法，将产生hash碰撞的元素都链接到同一个链表中【形成链表结构】
-
再Hash法，将产生hash碰撞的元素再采用不同的哈希算法进行处理，直至没有哈希冲突。
-
建立公共溢出区，把哈希表分为基本表和溢出表，将产生哈希冲突的元素存储到公共溢出表
-
开放寻址法：将产生hash碰撞的元素，去寻找一个新的空闲的哈希地址
开放寻址又包含了
1线性探测法：就是将在得到的hash值进行加1然后对数组长度取模，直到直到新的位置。
公式：h(x)=(Hash(x)+i)mod (Hashtable.length);（i会逐渐递增加1）
2平方探测法（二次探测）：就是将在得到的hash值进行依次为+(i^2)和-(i^2)然后对数组长度取模，直到直到新的位置。
公式：h(x)=(Hash(x) +i)mod (Hashtable.length);（i依次为+(i^2)和-(i^2)）
说说 数组，链表，循环，嵌套循环的时间复杂度
时间复杂度是用来度量算法执行的时间长短，一个算法花费的时间与算法中语句的执行次数成正比例
通常我们用Ｏ(f(n))渐进时间复杂度来衡量，比如说
eg：如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同，但时间复杂度相同，都为O(n2)。
-
要在 hash 表中找到一个元素就是 O(1)
-
要在无序数组中找到一个元素就是 O(n)
-
访问数组的第 n 个元素是 O(1)
-
二分搜索的时间复杂度最好的情况是 O(1)，最坏情况（平均情况）下 O(log n)
-
访问链表的第 n 个元素是 O(n)
-
一个For循环是O(n)
-
两个For循环嵌套是O(n2)
-
三个Foreach嵌套是O(n3)
JDK中线性结构的集合有哪些？
线性结构：元素存在一对一的相互关系
数组：按照顺序存储结构进行存储，ArrayList
链表：按照链式存储结构进行存储，LinkedList
栈和队列(超详细Java实现)_努力写代码的菜鸟的博客-CSDN博客
栈：按照FILO先进后出线性存储结构，
分为用数组实现的顺序栈【底层使用的数组实现】，用链表实现的链栈【底层使用的链表实现】
队列：FIFO先进先出的线性存储结构
分为顺序队列【使用顺序结构实现】和链式队列【使用链表结构】
串：特殊的线性存储结构，String【byte[]数组】，StringBuffer【Object动态数组】，StringBuilder
什么是树【树的定义】？
树是一个数据结构，它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树
你说一下树形结构和线性结构的优势？
线性结构【一对一连接】
线性结构中，无论是数组，还是链表，每个节点的左边和右边最多有一个节点。对于大量的输入数据，查询的时间比较长，效率低。
树形结构的优势在于它查找数据性能很高 【查询数据不用查询链表这么多次】
说一下树的分类，以及你对它们的理解（二叉查找树的优缺点，平衡树的优缺点，红黑树的优缺点，B-树的优缺点 ，B+树的优缺点）平衡树 ，红黑树【还没有理解归纳成自己的知识】
树有二叉树，多叉树，他们特点如下
-
二叉树【无序】：树中任意节点最多只有两个分叉的树，它又分为二叉排序树，平衡二叉树，赫夫曼树，红黑树
-
二叉排序树【有序】
-
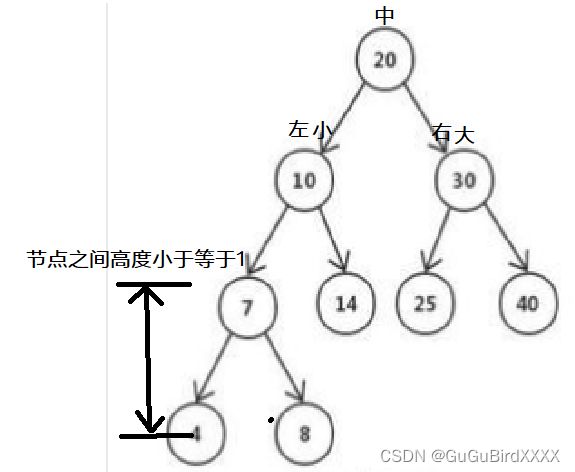
它是一个有序的二叉树，优势在于查找插入数据的性能很高【因为是有序的，总是采用左子节点（小），父节点(中)，右子节点(大)的顺序来存储元素 】，但是如果存储数据过大，二叉顺序树可能会出现倾斜，【倾斜部分】从而又形成链表结构。
-
-
平衡二叉树【Balance Binary Tree】
-
用来解决二叉排序树出现倾斜的问题，要求任何节点的高度差不大于1。它的查询性能很高，但是每次增删元素，会重排序导致性能低（因为需要保证节点之间高度差不大于1，就要重新进行平衡度计算，非常耗时。）。
-
-
红黑树【Red Black Tree】
-
自平衡二叉树【在平衡二叉树的基础上，避免了每次删除和添加要进行大量的平衡度计算，因为比较耗时】，要求根节点和叶子节点是黑色，其他节点红黑交替，在任何一个子树中，从根节点向下走到空节点的路径经过的黑节点数相同【强行为了自平衡，会在没有数据的节点加上一个null空节点，避免去进行重新计算排序】。从而保证了平衡。它的查询性能比平衡二叉树稍低，插入和删除元素的性能大幅提高。
-
HashMap为什么选择红黑树？
主要是因为红黑树的优点，因为hashmap更多的使用场景是添加和删除，如果使用平衡二叉树，每次添加和删除都会为了维持保证二叉树的平衡会进行大量的平衡度计算，比较耗时，而红黑树是采用着色的方式，保证从每一个链路从根节点开始到叶子节点的路径经过的黑节点都是一致的，不一致就采用null空节点进行补充，从而避免去进行大量的平衡度计算，带来时间的损耗。
多叉树：
解决二叉树存储大规模数据时，深度过大而导致IO性能低，查询效率低的问题，常见有B树和B+树，字典树，后缀树等等
-
B树【Balance Tree】
-
是一种自平衡的树，每个节点可以存储超过两个元素，可以有超过两个的子节点。
适用于数据量读写比较大的场景，比如文件系统，数据库索引。对于B-树来说，节点存储key【key为表中数据的主键】越多，分叉越多，需要的节点越少，树高越矮，IO次数少，查询效率越高。
-
B+树
-
B树升级版，它的内部节点只存储key，不存储具体数据【从而可以存储更多的key】，叶子节点存放key【key为表中数据的主键】和具体数据。这就使得每个节点可以存更多的key，树的高度更低，查询更快，同时它每次查询都会到叶子节点，查询速度更稳定。并且所有的叶子节点会组成一个有序链表，方便区间查询
有了二叉树为什么要出现多叉树？
因为二叉树【每个结点最多有两个子结点】在大规模的数据存储中，树会高的没谱，这会导致IO读写过于频繁，查询效率低下
多叉树【每个结点可以有多个子结点】，它又分为B树和B+树，都是自平衡的树，而且多叉树每个节点可以存储更多的key，因此能大幅度降低树的深度，提高查询性能
b-tree和b+tree的区别？
一是节点存储内容上的区别：B树每个节点都可以存放key和数据，而B+树所有内部节点只存放key【key为表中数据的主键】，叶子节点存放key和数据，因此它的节点能存放更多的key，降低树高，查询性能更快【key和数据，key可以存更多，数据只能存更少】
二是B+树所有的叶子节点会构成一个有序链表结构，方便区间查找和排序
说一下ES用到了什么数据结构？
ES是使用了数据索引存储结构，底层采用的是倒排索引文档。可以实现快速检索。
倒排索引文档原理：
1先对分档的每行内容进行索引编号，再对文档的每行内容进行分词
2再对一些标点符号去除，大小写时态转换等优化处理，
3最后按照字母顺序进行去重排序，最终形成一个倒排索引文档，
4我们在检索时，就可以通过二分查找的方式进行查找。
二分查找：二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x（索引）做比较，如果x=a[n/2],则找到x,算法中止
算法+二分查找+冒泡排序+位运算【Interview】_GuGuBirdXXXX的博客-CSDN博客
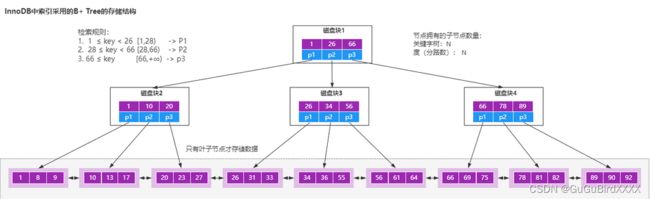
Mysql为什么用B+Tree作为索引的存储结构
常规的数据库存储引擎，一般都是采用B树或者B+树来实现索引的存储。
因为B树是一种自平衡树，用这种存储结构来存储大量数据，它的整个高度会相比二叉树来说，会矮很多。【因为是自平衡的，而且节点可以存储更多的key和数据，树的高度就会越低，读取效率就会更高。】
树的高度能够决定磁盘IO的次数，磁盘IO次数越少，读取速度就越快。
B+树就是对B树的一个增强。也就是B+树来作为索引和数据的存储结构。
相比较于B树结构，B+树做了几个方面的优化。
-
B+树的所有数据都存储在叶子节点，非叶子节点只存储索引【key为表中数据的主键】，从而每个节点可以存储更多的索引（key）。树的深度就会更低，查询效率就会更高。
-
叶子节点中的数据使用双向链表的方式进行关联，可以进行范围查找。
-
结论：在数据检索方面，所有数据都存储在叶子节点上，所以B+树在扫描过程中只需要扫描叶子节点【有序链表】，而B树需要遍历整个树。