扫描线板子 小思路
前言:
本板子是结合我的线段树1板子和OIWIKI的扫描线写成的类。
线段树1板子 区间加-CSDN博客
扫描线 - OI Wiki (oi-wiki.org)
背景:
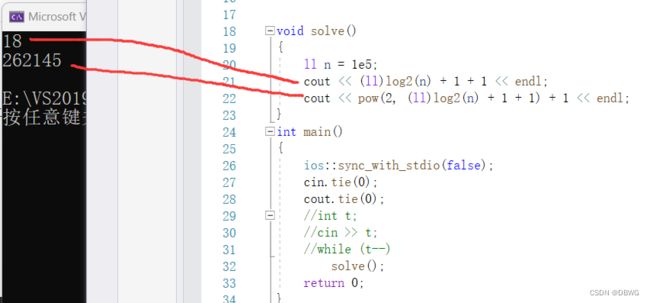
照着OI WIKI打了一遍,结果洛谷交上去RE,查了半天查不出来,最后看讨论区,给线段树大小再乘个2,就过了。。
我还数组以为太大了呢
本题数组并不大:
本题的xy是坐标,看的是坐标间的长度,应该是线段树进行二分的时候都要有mid,所以会多分几次。
扫描线原理:
我们从下往上扫吧。
1.
离散化就是把出现的x坐标放到数组里,排好序,数组里只有我们要的x。
离散化x后对这个数组进行建树。
2.
然后我们从下往上是根据y坐标进行的,所以每个y捆绑对应的x1,x2,以及加或减。
//这就是整个策略了。
代码:
#define ll long long
#define endl "\n"
#define int long long
const ll inf = 1e9;
template
class ST//segment tree
{
struct node
{
T l, r, sum;
T t;//懒标记//服务后代
node() :l(0), r(0), sum(0), t(0)
{}
};
ll n;
vectora;
vectord;
//扫描线中,上面的node中的l,r代表矩形左右
//下面的l,r是线段树的下标,每个a表示的是一个横坐标
public:
void push_up(ll i)
{
if (d[i].t > 0)//扫描到了
d[i].sum = d[i].r - d[i].l;
else
d[i].sum = d[i * 2].sum + d[i * 2 + 1].sum;
}
//直到最左和最右范围,但是不知道其中的和
void build_tree(ll i, ll l, ll r)
{
ll mid = l + (r - l) / 2;
if (l + 1 < r)
{
d[i].l = a[l];
d[i].r = a[r];
build_tree(i * 2, l, mid);
build_tree(i * 2 + 1, mid, r);
push_up(i);
}
else
{
d[i].l = a[l];
d[i].r = a[r];
d[i].sum = 0;
}
}
void update(ll l, ll r, ll val)
{
_update(1, l, r, val);//加并挂标记
}
void _update(ll i, ll l, ll r, ll val)
{
if (d[i].l == l && d[i].r == r)
{
d[i].t += val;
push_up(i);
return;
}
else
{
//中分
if (d[i * 2].r > l)
_update(i * 2, l, min(d[i * 2].r, r), val);//r在下一个内就不多传了
if (d[i * 2 + 1].l < r)
_update(i * 2 + 1, max(l, d[i * 2 + 1].l), r, val);
push_up(i);
}
}
T get_sum()
{
return d[1].sum;
}
ST(vectorarr)
{
a = arr;
n = a.size() - 1;
d = vector(2*pow(2, (ll)log2(n) + 1 + 1) + 1);
build_tree(1, 1, n);
}
};
struct scanline
{
int l, r, h;
int mark;
bool operator <(const scanline b)const
{
return h < b.h;
}
};
//总的sum统计了此刻矩形的长度,update一直在更新这个长度
void solve()
{
int n; cin >> n;
vectorxaxis;
vectoryaxis;
//x离散化用来服务线段树
//y该多少个就多少个,遇到就改,离散化了求得高度差,同层是0
//该加加,该减减,区间求和改成求长度吧
xaxis.push_back(0);
yaxis.push_back({});
for (int i = 1; i <= n; i++)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
xaxis.push_back(x1);
xaxis.push_back(x2);
yaxis.push_back({ x1,x2,y1,1 });
yaxis.push_back({ x1,x2,y2,-1 });
}
sort(xaxis.begin() + 1, xaxis.end());
sort(yaxis.begin() + 1, yaxis.end());
unique(xaxis.begin() + 1, xaxis.end());
ST demo(xaxis);
int ans = 0;
for (int i = 1; i < yaxis.size() - 1; i++)//最后一次不用算了
{
demo.update(yaxis[i].l, yaxis[i].r, yaxis[i].mark);
ans += demo.get_sum() * (yaxis[i + 1].h - yaxis[i].h);
}
cout << ans;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t = 1;
//cin >> t;
while (t--)
{
solve();
}
return 0;
}