归并排序+非比较排序
Hello everyone!欢迎来到排序章节目前的“终章”——归并排序,经过了前面三种排序的敲打,尤其是快速排序,相信你一定可以闯过这最后一关!
归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
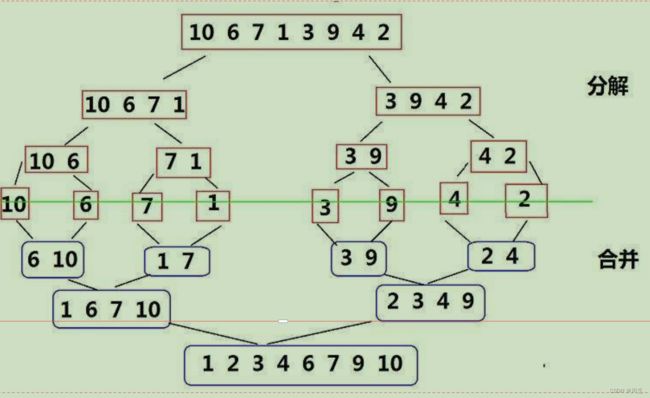
可以看到步骤是这样的:首先把原来的数据对半分开,然后继续对半分,直到一个部分只剩下一个元素;然后,在合并的过程中,一个合成两个,两个合成四个,在合成的过程中都变的有序,最后拼接在一起。
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
归并排序中,临时数组(也被称为辅助数组)的作用是用于临时存储排序过程中的中间结果。当归并排序对数组进行排序时,它需要额外的空间来临时存放排序的结果,以便将排好序的子数组合并为更大的数组。
具体来说,在归并排序的合并阶段,临时数组用于暂时存储已排好序的子数组的元素,然后再将排好序的子数组合并为更大的有序数组。
void _MergeSort(int* a, int begin, int end, int* tmp)
{
// 递归退出条件
if (begin >= end)
return;
// 求中点
int mid = (begin + end) / 2;
// 递归排序左右两部分
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
// 合并两个有序数组
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
// 按顺序将较小的元素放入临时数组中
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
// 将剩余元素补充到临时数组中
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
// 将排好序的临时数组拷贝回原数组
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
// 归并排序
void MergeSort(int* a, int n)
{
// 分配临时数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
// 调用递归排序函数
_MergeSort(a, 0, n - 1, tmp);
// 释放临时数组空间
free(tmp);
}
归并排序(非递归版本)
有些同学看到非递归,也许会想到在快排中我们使用了栈作为模拟递归的容器,于是认为我们在这里也会使用栈来用。可是在这里会出现一个问题,那就是当我们分解到只有一个数的时候,其是无法进行排序返回的,不像递归,所以会造成原数组后面的一部分被随机值占据。在这里我们要用到的是什么呢,答案是循环
我们设定一个值叫gap(步长),表示为2*gap个元素归并为1组,例如gap=1就是2个元素归并为一组,gap=2就是4个元素归并为一组。我们不需要将其拆解,而是在一开始就把它们当成独立的个体去归并,就像这样

比如gap=1时,我们就会得到6 10 1 7 3 9 2 4的返回结果,而gap=2时,就会得到1 6 7 10 2 3 4 9的结果,直到gap=4时最终排序结束得到结果
这样写的话,我们就能得到这样的结果:
void MergeSortNonR(int* a, int n) {
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n) {
for (int i = 0; i < n; i += 2 * gap) {
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
tmp[j++] = a[begin1++];
}
else {
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1) {
tmp[j++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * 2 * gap);
}
gap *= 2;
}
free(tmp);
}
这样写,对于我们刚才的数组来说,运行起来排序是相当可以的,可是,我们如果把数组的个数改变,改成不是2的次方的个数,我们就会发现,程序崩溃了,这是为什么呢?举个例子给大家看看
我们先创建这样一个数组:10 8 7 1 3 9 4 2 9 10,这里面包含了10个元素,显然不是2的次方个数,然后我们再对部分代码进行修改:
while (gap < n) {
printf("gap:%d->",gap);
for (int i = 0; i < n; i += 2 * gap) {
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//[begin1,end1][begin2,end2]归并
printf("[%d %d][%d %d]",begin1,end1,begin2,end2);
int j = begin1;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
tmp[j++] = a[begin1++];
}
else {
tmp[j++] = a[begin2++];
}
}
当我们修改了代码之后,再次运行程序,就会输出这样的语句:

我们发现,标红的地方都有数组的越界,也难怪我们无法给其排序,并且造成程序的崩溃,那么,面对这些问题,我们要怎么处理呢?
我们会发现,除了begin1,end1、begin2、end2都有可能越界。面对end1,其越界证明前面的元素已经排序好了,后面没有数据可以处理,所以可以直接退出此次循环;而begin2也是一样的,前面的数据已经排好了;而end2不同,我们需要将其限制范围为n-1 。修改这些之后,也别忘了将memcpy的内存范围进行修改,更改为end2-i+1
代码如下:
void MergeSortNonR(int* a, int n) {
// 申请临时数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n) {
// 将数组分为若干组并进行合并
for (int i = 0; i < n; i += 2 * gap) {
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// 处理边界情况
if (end1 >= n || begin2 >= n) {
break;
}
// 处理右边子数组越界情况
if (end2 >= n) {
end2 = n - 1;
}
// 归并排序合并操作
int j = begin1;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
tmp[j++] = a[begin1++];
} else {
tmp[j++] = a[begin2++];
}
}
// 将剩余元素复制到临时数组
while (begin1 <= end1) {
tmp[j++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[j++] = a[begin2++];
}
// 将排好序的临时数组拷贝回原数组
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2; // 增加步长进行下一轮合并
}
free(tmp); // 释放临时数组内存
}
归并排序的应用
我们知道,排序分为外排序和内排序,外排序就是在硬盘(文件)中进行排序,而内排序就是在内存中进行排序。我们之前学过的如插入排序,交换排序等等一系列都是内排序,但唯独归并排序既可以作为内排序,还可以用作外排序。
我们知道,内存的特点就是小/快/价格规格贵/带电存储,而硬盘则是大/慢/价格规格便宜/不带电存储,所以当我们想要排序文件中的庞大数据时,我们必定会用到归并排序
假设我们电脑的内存为4G,而现在我需要排序一个16G的文件,这个时候,我们就会每次读4G数据到内存中用之前我们学过的如希尔排序、堆排序、快速排序等等方法对其进行排序,(fscanf)写到一个小文件中去;而这样写了四个文件后,它们就可以两两归并(fprintf),再两两归并,最终合成一个有序的16G大文件
如果笔者日后有时间,会为大家在以后补充这种这段应用的代码供大家参考,期望大家的关注!
非比较排序
刚才我们学习的,全都是需要比较才可以使用的排序方法,而这时候我们要学习的一种方法叫做非比较排序。大家第一次听一定会觉得很奇怪,什么?不比较也能知道各个元素的顺序吗?等下就为大家揭开非比较排序的原理!
非比较排序中大家听的比较多的是基数排序,计数排序和桶排序,但在这篇文章中,我们只讲计数排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
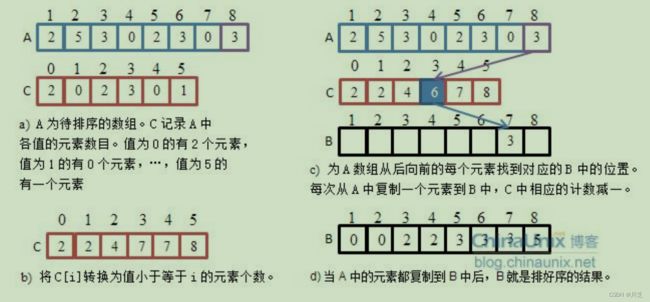
就比如我们要排序一个1 3 9 1 5 1 2 3的数组,我们创建一个count数组来记录其每个值的出现次数,并在后面遍历count数组的时候直接把值输出,从最小值到最大值。因为数组的排序本身从小到大的,所以输出的时候顺序也是正序的。但这里的数很小很小,试问如果我们要排序1000~1999的值,我们不可能按照其真实值开辟一个2000int型大小的空间,那样前面的空间就会造成浪费,而这样子的方法也叫做绝对映射,也就是值对应的下标就是其值的大小;为了防止这种浪费,我们会使用相对映射,范围大小为max-min,而count的下标就设置成这个样子:count[a[i]-min],这样就可以保证,数组依然是从零开始存储,不会浪费空间,代码如下:
//计数排序
//时间:O(N+range)
//空间:O(range)
//相对映射解决了负数的问题同时,这个大家可以自己带值进去看
void CountSort(int* a, int n) {
int min = a[0], max = a[0];
for (int i = 0; i < n; i++) {
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));//calloc创造时所有元素置为0
if (count == NULL) {
perror("calloc fail");
return;
}
//统计次数
for (int i = 0; i < n; i++) {
count[a[i] - min]++;//相对位置奥
}
//排序
int i = 0;
for (int j = 0; j < range; j++) {
while (count[j]--) {
a[i++] = j + min;//把值还原咯
}
}
}
并且我们可以发现,在N和range的大小相似时,这个排序甚至可以近似于O(N)的时间复杂度,在某些特定情况下发挥超常,平时我们一般用的还是我们之前讲到的几种排序
计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 稳定性:稳定
排序总结
经过之前的选拔,你已经成功通过了排序闯关,接下来看看总结,看看你有没有忘记什么(doge)
①直接插入排序:直接插入排序是一个一个从后面插入,并与前面的值比较,逆序的时候(最差情况),要排升序就需要从头到尾都要移动,逐次移动1+2+3+…n-1次,是一个标准的等差数列,所以时间复杂度O(n^2);没开额外空间,所以空间复杂度O(1);
- 说到稳定性,在这里先要提醒一下大家,这可指的不是性能的波动,而是数组里面有相同的值,保证其相对顺序不变就是稳定的。就比如一个5在另一个5后面,在排序之后还能保持这1个5在另一个5的后面,那就说明其是稳定的。
- 举个例子,如果我们要给同样排名的同学发奖品,可是排名数相同的同学太多了,我们这个时候就按照一开始的交卷顺序来看,那我们肯定不希望自己原本在可以拿到奖品的位置,后面却被别人顶替掉了,这个时候稳定性就十分重要了。
- 再延申出来一个例子,假如我们给结构体排序。比如我们超市要上架一批同样效果的竞争产品,但其评分不同,给超市的佣金也不同,这时候我们分高的依然在前面,但是评分相同的就要看谁给的佣金高,这怎么办呢?像下面这么做就可以啦。用金额排完降序之后,给钱高的必然排在前面,而后面再用稳定的排序对评分进行排序,9.0这种评分相同的原先按照金额排好的顺序就不会变。
②希尔排序:由于希尔排序先分组预排,再最后进行直接插入排序,无法准确的求出其精确的时间复杂度,所以直接按照O(N^1.3)来记;而空间复杂度自然也是O(1);稳定性:不稳定,预排序中,相同的值可能分在不同组,无法控制,举个例子:1 5 3 4 4 5 6 7 ,gap=3,一组是1 4 6,一组是5 4 7,一组是3 5,那么排序完就是1 4 6,4 5 7,3 5,顺序就会变成1 4 3 4 5 5 6 7,第二组中的4原本再第一组的后面,现在就蹦到了前面。
③选择排序:选择排序的方法是依次选最大的数放在左边,最小的数放在右边,然后交换,本质上时间复杂度依然是等差数列,O(N^2);空间O(1);稳定性:选择排序看似稳定,但实际上我们模拟一个情景,9…9…5…5,假设9就是最大的数,那么我们把右边的9跟最右边的5交换,两个9的相对位置没有变,但是两个5的相对位置很明显发生了变化,所以并不稳定
④堆排序:时间复杂度O(N*logN),在堆排序中,建堆操作的时间复杂度为 O(n),而排序过程中涉及的比较和交换的次数也是 O(n log n);空间复杂度O(1);稳定性:不稳定,就比如2 2 2 1 0这个数组,建堆时会生成这样的堆。
于是,当开始排序的时候,顶上的2就会与0换位置,相对位置就会明显发生改变。
⑤冒泡排序:时间复杂度O(n^2),标准的等差数列;空间复杂度O(1);稳定性:稳定,毕竟遇到相同大小的并不会往后交换
⑥快速排序:时间复杂度O(nlogn),在最好的情况下,快速排序的时间复杂度是 O(n log n)。这是当每次递归调用都能将数组大致分成两半时的情况。在最坏的情况下,快速排序的时间复杂度是 O(n^2)。这通常发生在输入数组已经排序或接近排序时。而空间复杂度的计算,我们在快速排序中,递归的深度通常是logn,我们在递归时,递归完左边的,递归右边时空间会重复利用,并且空间并不会累积,空间复杂度不看累计看深度,故其空间复杂度为O(logn);稳定性:不稳定,因为虽然比key大的值在右边,比key小的值在左边,但是相等的值既可能在左边也可能在右边,并且我们用三数取中优化算法的时候,就已经有可能出现替换了
⑦归并排序:时间复杂度O(nlogn);空间复杂度O(n),因为我们开辟了n个临时空间;稳定性:稳定,但是要在原有的基础上将小于改成小于等于
eg.nlogn时间复杂度的逻辑都是二分的逻辑思想
从这里开始排序这个栏目就正式结束了,但我们的学习并不会在这里终止,往后的路是星辰大海!欢迎来到下一个栏目,C嘎嘎!大家多多关注啦!

