java七大排序---冒泡排序、快速排序
前言
一、冒泡排序
1.认识冒泡排序
2.冒泡排序代码展示
1.注意事项:
二、快速排序
1.原理总概
2.随机化快排
1.代码展示
3.二路快排
1.排序流程演示:
2. 代码展示
3.三路快排
1.排序流程演示:
2.代码展示:
4.注意事项:
总结
前言
对于快速排序和冒泡排序,都是基于交换的排序思想。
一、冒泡排序
1.认识冒泡排序
冒泡排序的大体的思路:在无序的区间,通过相邻数字的比较,将最大的数冒泡到数组的最后,持续这个过程,直到整个数组有序。
冒泡排序的动图过程如下:
2.冒泡排序代码展示
//冒泡排序
public static void bubbleSort(int[] arr) {
//代表应该执行多次的交换
for (int i = 0; i < arr.length - 1; i++) {
//优化:当遍历一次结束时,没有发生一次交换,则数组是有序的,直接结束排序
boolean isSorted = false;
//每一次交换需要比较的元素的个数
for (int j = 0; j < arr.length - 1 - i; j++) {
//这一步没有加上等于,就是保证了排序的稳定性
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
isSorted = true;
}
}
if (!isSorted) {
break;
}
}
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}1.注意事项:
1.对于第二次的for循环,因为是arr[j] 和arr[j+1]的比较,所以对于 j 来所,第一次的循环应该是 j < arr.length -1 ,此时的 i == 0。
2.对于冒泡排序的稳定性保证,就是遇到相等的元素不交换。
3.对于冒泡排序的优化,一次遍历结束,isSorted 依旧是false,说明在遍历中没有发生一次交换。
4.时间复杂度O(n^2)。
二、快速排序
1.原理总概
1. 从待排序区间选择一个数,作为基准值(pivot).
2. Partition: 遍历整个待排序区间,将比基准值小的(可以包含相等的)放到基准值的左边,将比基准值大的(可以包含相等的)放到基准值的右边。
3. 采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度 == 1,代表已经有序,或者小区间 的长度 == 0,代表没有数据。
2.随机化快排
随机化快排与普通的快排的差异在于对于基准值的选取,随机化快排对区间里,随机的对索引进行选取,而普通快排选择第一个元素或者最后一个元素,这样的当数组在接近有序的情况下,就会产生严重的分区不平衡,也就是可以看作一个二叉树只有一条链子的情况,时间复杂度会降低为O(n^2)。
1.代码展示
private static final ThreadLocalRandom random=ThreadLocalRandom.current();
//快速排序-----解决在接近有序的数组上排序的情况
public static void quickSort(int[] arr){
quickSortInternal(arr,0,arr.length-1);
}
private static void quickSortInternal(int[] arr, int l, int r) {
if(l>=r){
return ;
}
int p=partition(arr,l,r);
quickSortInternal(arr,l,p-1);
quickSortInternal(arr,p+1,r);
}
private static int partition(int[] arr, int l, int r) {
int randomIndex= random.nextInt(l,r);
swap(arr,l,randomIndex);
int v=arr[l];
int j=l;
for(int i=l+1;i<=r;i++){
if(arr[i]上述的代码在重复元素较多的情况下,也会产生分区不平衡,所以引入二路快排
3.二路快排
二路快排将相等的元素均匀的分到左右两个子区间。
1.排序流程演示:
2. 代码展示
//二路快排-------避免大量重复的元素在集合上;
public static void quickSort2(int[] arr){
quickSortInternal2(arr,0,arr.length-1);
}
private static void quickSortInternal2(int[] arr, int l, int r) {
if(l>=r){
return ;
}
int p=partition2(arr,l,r);
quickSortInternal2(arr,l,p-1);
quickSortInternal2(arr,p+1,r);
}
private static int partition2(int[] arr, int l, int r) {
int randomIndex=random.nextInt(l,r);
swap(arr,randomIndex,l);
int v=arr[l];
int i=l+1;
int j=r;
while(true){
//这里需要注意一下子,arr[i]<=v 的话,就会使排序的效率降低
//因为如果遇到和v相等的不交换会出现分区不平衡的情况
while(i<=j&&arr[i]v){
j--;
}
if(i>j){
break;
}
swap(arr,i,j);
i++;
j--;
}
swap(arr,l,j);
return j;
} 3.三路快排
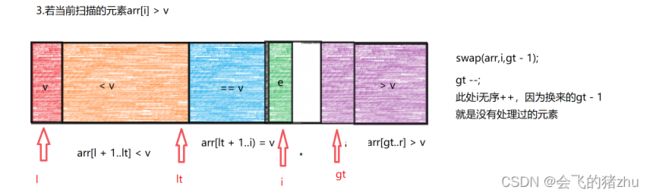
在一次的函数分区中,将所有相等的元素都放在最终位置,只需要在大于 V 和小于 V 的子区间上进行快排,所有相等的元素就不处理了。
1.排序流程演示:
2.代码展示:
//三路快排
public static void quickSort3(int[] arr){
quickSortInternal3(arr,0,arr.length-1);
}
private static void quickSortInternal3(int[] arr, int l, int r) {
if(l>=r){
return ;
}
int randomIndex=random.nextInt(l,r);
swap(arr,randomIndex,l);
int v=arr[l];
//这里lt指向v的最后一个位置
int lt=l;
int gt=r+1;
int i=lt+1;
while(iv){
swap(arr,i,--gt);
}else{
i++;
}
}
swap(arr,l,lt);
quickSortInternal3(arr,l,lt-1);
quickSortInternal3(arr,gt,r);
} 4.注意事项:
1.快速排序是不稳定的。
2.时间复杂度O(nlogn)。
3.当出现排序集合重复元素不多时,随机化快排就可以解决问题;当出现待排序集合有大量重复的元素时,选择二路、三路快排,优化重复元素。
总结
加油哦~~~