【Algorithms 4】算法(第4版)学习笔记 03 - 1.3 背包、队列和栈
文章目录
-
- 前言
- 参考目录
- 学习笔记
-
- 0:预热
- 1:栈
- 1.1:栈的链表实现
- 1.1.1 代码实现
- 1.2:栈的数组实现
- 1.2.1:定容栈
- 1.2.2:可调整大小数组
- 1.2.3:代码实现
- 1.3:链表与数组的取舍
- 2:队列
- 2.1:队列的链表实现
- 2.1.1:代码实现
- 2.2:队列的数组实现
- 3:泛型
- 4:迭代
- 4.1:链表迭代器实现
- 4.2:数组迭代器实现
- 4.3:`Iterable` 接口与 `Iterator` 接口
- 5:栈的应用
- 5.1:Dijkstra 双栈算法 demo
- 5.1.1:代码实现
前言
这一章节比较基础,但是也十分重要,栈以及队列都是 Java 开发中非常熟悉的底层结构了。虽然标题有背包(Bags),但实际上 Sedgewick 教授讲解的内容主要还是栈和队列,尤其是栈。
参考目录
- B站 普林斯顿大学《Algorithms》视频课
(请自行搜索。主要以该视频课顺序来进行笔记整理,课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。) - 微信读书《算法(第4版)》
(本文主要内容来自《1.3 背包、队列和栈》) - 官方网站
(有书本配套的内容以及代码)
学习笔记
注1:下面引用内容如无注明出处,均是书中摘录。
注2:所有 demo 演示均为视频 PPT demo 截图。
0:预热
先来回顾一下最基础的内容。
栈:后进先出 LIFO - last in first out
- 入栈
push - 出栈
pop
队列:先进先出 FIFO - first in first out
- 入队
enqueue - 出队
dequeue
在后续的实现方法中就是以上面的作为方法的命名。
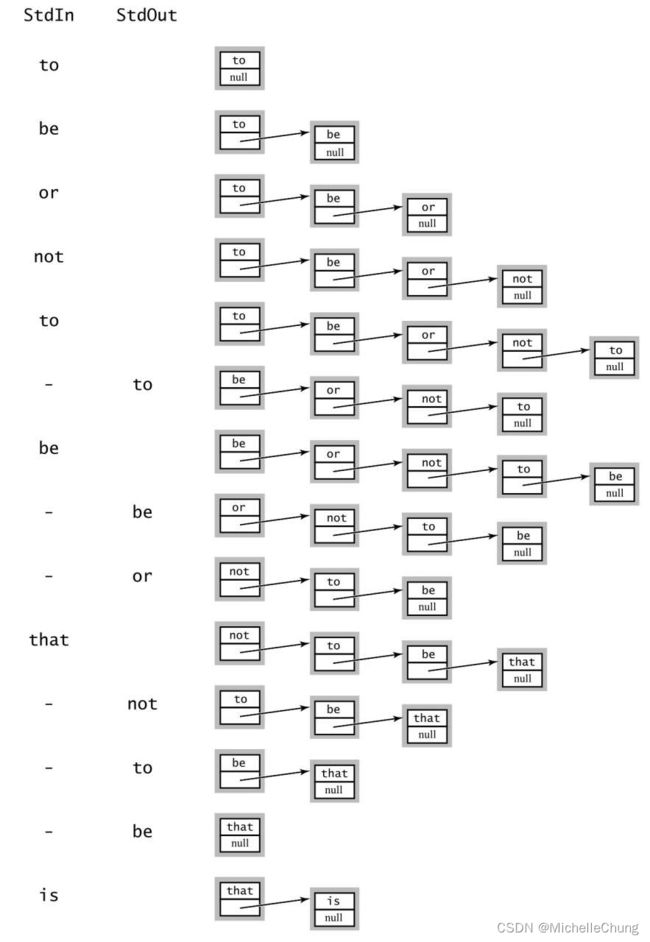
在本章节中,无论是栈或者是队列,都使用了一个 demo 进行说明:
读取一系列字符,如果是"-",字符 出栈/出队 并打印;
否则,字符 入栈/入队。
1:栈
先来看看栈实现的大致效果:
下面按照不同的实现方式进行分析。
1.1:栈的链表实现
对应章节《1.3.3 链表》
官网有分步骤实现的图,太长了这里就不贴了,留个 传送门。
1.1.1 代码实现
edu.princeton.cs.algs4.LinkedStack
edu.princeton.cs.algs4.LinkedStack#push
edu.princeton.cs.algs4.LinkedStack#pop
1.2:栈的数组实现
实现方式:
- 使用一个数组
s[]存储栈的 N 个条目 push():在s[N]上添加一个新的条目pop():从s[N-1]中移除一个条目
注:数组需要考虑容量大小问题,当N容量超过了数组的长度,会造成栈溢出。
1.2.1:定容栈
对应章节《1.3.2.1 定容栈》
表1.3.2 一种表示定容字符串栈的抽象数据类型
(FixedCapacityStackOfStrings这个类jar包没有源码)
这里补充一个比较细节的点 —— 对象游离:
对应章节《1.3.2.4 对象游离》
对象游离,不再需要的对象依然持有引用,导致无法进行垃圾回收。
1.2.2:可调整大小数组
对应章节《1.3.2.3 调整数组大小》
前面关于数组实现的说明中有提及,需要注意数组的大小问题,因此需要对数组的长度进行动态调整。
教授列举了两种方式。
第一种方式:
push():数组长度加1pop():数组长度减1
但是这种方式可以看出来 开销非常大,插入一个值所需要的时间约为:1+2+3+……+N ~ N2/2。
第二种方式:
反复加倍。
每次达到最大长度后,数组长度增加一倍。
push():当数组满了,长度变为2倍pop():当数组的内容只有一半时,长度减半
开销约为:N+(2+4+8+……+N) ~ 3N
第二种方式相较于第一种方式有了明显的提高,但是还有一个问题 —— 抖动。
抖动什么意思?可以设想一种最坏的情况:
反复交替入栈和出栈。
这样子的开销也是很难接受的,因而有了更进一步的优化:数组变为 1/4 长度时再减半。
最终效果:
1.2.3:代码实现
edu.princeton.cs.algs4.ResizingArrayStack
edu.princeton.cs.algs4.ResizingArrayStack#push
edu.princeton.cs.algs4.ResizingArrayStack#pop
edu.princeton.cs.algs4.ResizingArrayStack#resize
1.3:链表与数组的取舍
有上面两种实现方式之后,需要如何进行选择,下面来分析一下。
链表实现:
- 最坏的情况下,每次操作有固定时间。
- 使用额外的时间和空间处理链。
可调整数组实现:
- 每次操作固定的摊销时间。
- 更少空间浪费。
顺便贴一下通义的总结吧:
栈(Stack)是一种后进先出(LIFO)的数据结构,常见的实现方式有两种:可调整大小的数组和链表。下面分别分析这两种实现方式的优缺点及适用场景:
-
可调整大小的数组(动态数组)实现栈:
- 优点:
- 操作速度快:由于数组支持随机访问,因此在栈顶进行插入(push)和删除(pop)操作的时间复杂度为O(1)。
- 内存连续:数组元素存储在内存中是连续的,有利于CPU缓存优化,提高数据读取效率。
- 缺点:
- 空间利用率:如果预先分配的数组空间不足,需要动态扩容,这可能涉及到复制整个现有栈到新的、更大的数组中,虽然大多数现代语言的库已经对此做了优化(如自动扩容),但在极端情况下仍可能导致性能损失。
- 最大容量限制:尽管是可调整大小,但理论上存在一个最大容量限制,尤其是对于固定大小的内存区域。
适用场景:
- 当栈内元素数量相对稳定或增长可预测时,动态数组实现的栈更为高效。
- 对于大量push/pop操作且对时间效率要求较高的场景,数组实现通常优于链表。
- 优点:
-
链表实现栈:
- 优点:
- 动态扩展:链表无需预先设定大小,当需要更多空间时可以轻松地添加新节点,不会造成内存浪费。
- 删除方便:链表中的元素删除只需改变指针指向即可,不需要移动其他元素。
- 缺点:
- 访问速度慢:链表不支持随机访问,查找或修改特定位置的元素需要从头节点开始遍历,时间复杂度为O(n),但对于栈顶操作,仍然可以保持O(1)。
- 额外的空间开销:每个链表节点都需要额外存储指向下一个节点的指针,增加了存储空间需求。
适用场景:
- 当栈内元素数量增长不确定或可能大幅度波动时,链表实现的栈更能适应动态变化。
- 对于栈的大小无法预知或者需要频繁进行插入删除操作而不在乎额外空间消耗的应用场景,链表实现栈也是一个合理选择。
- 优点:
总结来说,在大多数常见应用场景下,由于栈主要关注栈顶操作,数组实现因其简单高效的特性而更受欢迎。然而,如果考虑到空间使用上的灵活性或者有特殊的需求(比如栈的大小无法提前估计),链表实现则是一个更具弹性的选择。
2:队列
用教授的话说,这和栈的实现是一样的,所以很简单的带过了,简单整理一下相关的内容。
2.1:队列的链表实现
对应章节《1.3.3.9 队列的实现》
2.1.1:代码实现
edu.princeton.cs.algs4.LinkedQueue
edu.princeton.cs.algs4.LinkedQueue#enqueue
edu.princeton.cs.algs4.LinkedQueue#dequeue
2.2:队列的数组实现
edu.princeton.cs.algs4.ResizingArrayQueue
edu.princeton.cs.algs4.ResizingArrayQueue#enqueue
edu.princeton.cs.algs4.ResizingArrayQueue#dequeue
3:泛型
简单来说,泛型是为了满足同一实现对于不同类型的要求。
来看看代码 Javadoc 的说明:
值得注意的是,Java不支持泛型数组,因此需要进行类型强转,以之前的方法为例:
edu.princeton.cs.algs4.ResizingArrayStack#resize
教授的观点:
- 优秀的代码应该不用强制类型转换(A good code has zero cast.)
- 要尽量避免强制类型转换是因为它确实在我们的实现中留下隐患。
(例如:数据精度丢失、溢出、类型转换异常、类型不匹配、NPE 等) - 像这样简单的代码强制类型转换是讨厌的特性。
(ugly cast,an undesirable feature)
4:迭代
需要实现的是,允许客户端遍历集合中的元素,但不需要让客户端知道底层实现用的是链表还是数组或其他任何实现。
下面以栈的实现为例进行说明。
4.1:链表迭代器实现
edu.princeton.cs.algs4.LinkedStack.LinkedIterator
4.2:数组迭代器实现
edu.princeton.cs.algs4.ResizingArrayStack.ReverseArrayIterator
4.3:Iterable 接口与 Iterator 接口
这两个接口还是比较重要的,所以单拎出来说明一下。
java.lang.Iterable
java.util.Iterator
仔细看的话应该不难看出来两者的区别,不过为了便于理解,我又去整理了一下 ChatGPT 和 通义 的回答:
在Java中,Iterable接口和Iterator接口都与集合的迭代(iteration)有关,但它们分别承担不同的角色。
-
Iterable 接口:
Iterable接口是Java集合框架的根接口之一,它定义了一种表示可迭代对象(Iterable object)的标准方式。- 该接口中包含一个抽象方法
iterator(),该方法返回一个实现了Iterator接口的迭代器对象。 - 类实现了
Iterable接口的对象可以使用增强的for循环(foreach循环)进行遍历,因为foreach循环的底层实现是通过调用iterator()方法获取迭代器来实现的。
-
Iterator 接口:
Iterator接口是用于遍历集合中的元素的标准方式。它定义了一组方法,允许按顺序访问集合中的元素,而不暴露集合的内部结构。Iterator接口包含一些重要的方法,如hasNext()用于检查是否还有元素,next()用于获取下一个元素,remove()用于从集合中移除当前元素(可选)。
为什么在 Iterable 接口中需要定义 Iterator 接口呢?
-
这种设计方式符合单一职责原则,即一个接口只负责一个职责。
Iterable负责定义可迭代对象,而Iterator负责定义遍历这个可迭代对象的方式。这样的分离使得集合类可以选择性地提供不同类型的迭代器,而不必在可迭代接口中包含所有可能的遍历方法。 -
这种设计也符合 迭代器模式(Iterator Pattern),其中
Iterable表示聚合对象,而Iterator表示迭代器对象。这样的模式使得你可以在不暴露集合内部结构的情况下遍历集合中的元素。
总结来说,Iterable 是一个抽象的概念,表明一个类是可以被迭代的;而 Iterator 则是具体实现迭代行为的工具。这种分离的设计使得集合的遍历机制更加灵活,并且让集合的实现和遍历逻辑相互独立。
5:栈的应用
这一小节主要探讨了 Dijkstra 双栈算法的实现。
5.1:Dijkstra 双栈算法 demo
先来说说这个 Dijkstra 双栈算法,输入一组字符组成的表达式:
书本中给出的示意图是这样的:
但是说实话不太直观,直到看到视频里面教授 PPT 的动态演示,简直妙啊:
5.1.1:代码实现
我找到了官方的 代码实现,不过我想直接用 main 方法测试,所以稍微改了一下,贴在下面:
import edu.princeton.cs.algs4.Stack;
/******************************************************************************
* Compilation: javac Evaluate.java
* Execution: java Evaluate
* Dependencies: Stack.java
*
* Evaluates (fully parenthesized) arithmetic expressions using
* Dijkstra's two-stack algorithm.
*
* % java Evaluate
* ( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )
* 101.0
*
* % java Evaulate
* ( ( 1 + sqrt ( 5 ) ) / 2.0 )
* 1.618033988749895
*
*
* Note: the operators, operands, and parentheses must be
* separated by whitespace. Also, each operation must
* be enclosed in parentheses. For example, you must write
* ( 1 + ( 2 + 3 ) ) instead of ( 1 + 2 + 3 ).
* See EvaluateDeluxe.java for a fancier version.
*
*
* Remarkably, Dijkstra's algorithm computes the same
* answer if we put each operator *after* its two operands
* instead of *between* them.
*
* % java Evaluate
* ( 1 ( ( 2 3 + ) ( 4 5 * ) * ) + )
* 101.0
*
* Moreover, in such expressions, all parentheses are redundant!
* Removing them yields an expression known as a postfix expression.
* 1 2 3 + 4 5 * * +
*
*
******************************************************************************/
public class Evaluate {
public static void main(String[] args) {
String s = "( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )";
System.out.println("s = " + s);
evaluate(s.split(" "));
String s2 = "( ( 1 + sqrt ( 5 ) ) / 2.0 )";
System.out.println("s2 = " + s2);
evaluate(s2.split(" "));
}
public static void evaluate(String[] args) {
Stack<String> ops = new Stack<String>();
Stack<Double> vals = new Stack<Double>();
for (String s : args) {
// 读取字符
if (s.equals("(")) ;
// 如果是运算符则压入栈中
else if (s.equals("+")) ops.push(s);
else if (s.equals("-")) ops.push(s);
else if (s.equals("*")) ops.push(s);
else if (s.equals("/")) ops.push(s);
else if (s.equals("sqrt")) ops.push(s);
// 如果是")",则弹出运算符和操作数,计算结果并压入栈中
else if (s.equals(")")) {
String op = ops.pop();
double v = vals.pop();
if (op.equals("+")) v = vals.pop() + v;
else if (op.equals("-")) v = vals.pop() - v;
else if (op.equals("*")) v = vals.pop() * v;
else if (op.equals("/")) v = vals.pop() / v;
else if (op.equals("sqrt")) v = Math.sqrt(v);
vals.push(v);
}
// 如果字符既非运算符也不是括号,将它作为double值压入栈
else vals.push(Double.parseDouble(s));
}
System.out.println(vals.pop());
}
// 源代码
// public static void main(String[] args) {
// Stack ops = new Stack();
// Stack vals = new Stack();
//
// while (!StdIn.isEmpty()) {
// String s = StdIn.readString();
// if (s.equals("(")) ;
// else if (s.equals("+")) ops.push(s);
// else if (s.equals("-")) ops.push(s);
// else if (s.equals("*")) ops.push(s);
// else if (s.equals("/")) ops.push(s);
// else if (s.equals("sqrt")) ops.push(s);
// else if (s.equals(")")) {
// String op = ops.pop();
// double v = vals.pop();
// if (op.equals("+")) v = vals.pop() + v;
// else if (op.equals("-")) v = vals.pop() - v;
// else if (op.equals("*")) v = vals.pop() * v;
// else if (op.equals("/")) v = vals.pop() / v;
// else if (op.equals("sqrt")) v = Math.sqrt(v);
// vals.push(v);
// } else vals.push(Double.parseDouble(s));
// }
// StdOut.println(vals.pop());
// }
}
(完)