算法基础课-数学知识
质数
题目链接:866. 试除法判定质数 - AcWing题库
思路:1不是质数,枚举到根号n。
#include
using namespace std;
bool check(int num){
if(num == 1) return false;
for(int i=2;i<=num/i;i++){
if(num%i==0) return false;
}
return true;
}
int main(){
int n;
cin>>n;
while(n--){
int num;
cin>>num;
if(check(num)) cout<<"Yes"< 题目链接:867. 分解质因数 - AcWing题库
思路:如下。G07 分解质因数 唯一分解定理 试除法_哔哩哔哩_bilibili
#include
using namespace std;
void process(int num){
for(int i=2;i<=num/i;i++){
int cnt = 0;
while(num%i==0){
num/=i;
cnt++;
}
if(cnt) cout<1) cout<>n;
while(n--){
int num;
cin>>num;
process(num);
cout< 题目链接:868. 筛质数 - AcWing题库
思路:G08 筛质数 埃氏筛法 线性筛法_哔哩哔哩_bilibili
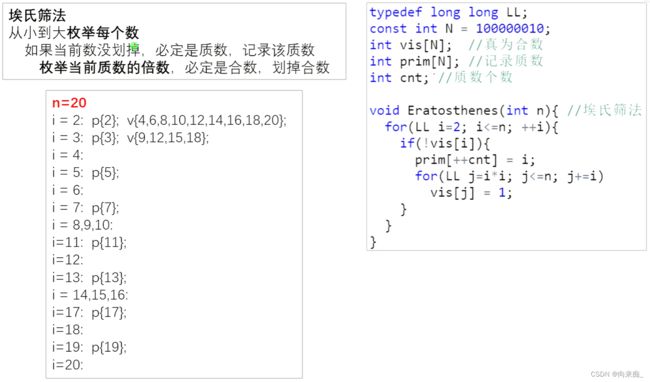
埃氏筛法,从2开始筛到目标数字n。当前数字若不是合数(使用st数组判断),则一定是质数,将其加入到质数数组中(p数组,并使用cnt计数)。若为质数时,使用当前质数干掉后面的合数(从质数的平方开始枚举)。总体时间复杂度为O(nloglogn)。
线性筛法,埃氏筛法中每个合数有可能被不同的质数筛掉。线性筛保证每个合数均被其最小的质因子筛除,从而保证所有的数字只被记录一次,时间复杂度降低为O(n)。实际情况中的时间优化并不明显。
#include
using namespace std;
typedef long long ll;
const int N = 1e6+10;
int p[N];
int cnt;
int n;
bool st[N];
// void prime(){
// for(int i=2;i<=n;i++){
// if(!st[i]) p[++cnt] = i;
// for(int j=1;1ll*i*p[j]<=n;j++){
// st[i*p[j]] = true;
// if(i%p[j] == 0) break;
// }
// }
// }
void prime(){
for(ll i=2;i<=n;i++){
if(!st[i]){
p[++cnt] = i;
for(ll j=i*i;j<=n;j+=i){
st[j] = true;
}
}
}
}
int main(){
cin>>n;
prime();
// for(int i=1;i<=cnt;i++) cout< 约数
题目链接:869. 试除法求约数 - AcWing题库
思路:需要注意的地方在于对于像4,9,25这样可以正好开方的数,对于其约数只需输出一个。
#include
using namespace std;
stack stk;
int main(){
int n;
cin>>n;
while(n--){
int num;
cin>>num;
for(int i=1;i<=num/i;i++){
if(num%i==0){
cout< 题目链接:870. 约数个数 - AcWing题库
思路:对输入的数分解质因数,并且记录在map中,最后统一处理。
约数个数如何求取?例如求360的约数个数,先进行因式分解。360可以由2^3*3^2*5^1得到。
那么他的约数可以从2中取值(0,1,2,3),乘从3中取值(0,1,2),乘从5中取值(0,1)得到。例如取2^0*3^0*5^0是1,1是360的约数。所以约数总的个数就是2的取值个数乘3的取值个数乘5的取值个数。
约数之和如何求取?同样的道理,也是从质因数中找数相乘,乘出来的结果一定是约数。将其相加即可。公式推导:约数和定理,约数个数定理_哔哩哔哩_bilibili
#include
using namespace std;
const int N = 110,mod = 1e9+7;
// int p[N];
int n;
unordered_map p;
int main(){
cin>>n;
while(n--){
int num;
cin>>num;
//分解质因数
for(int i=2;i<=num/i;i++){
while(num%i==0){
num/=i;
p[i]++;
}
}
if(num>1) p[num]++;
}
long long res = 1;
for(auto t : p){
res = res * (t.second + 1) % mod;
}
cout< 题目链接:871. 约数之和 - AcWing题库
思路:需要注意的是代码while (b -- ) t = (t * a + 1) % mod;,跟字符串哈希有相似之处。
#include
using namespace std;
const int N = 110,mod = 1e9+7;
// int p[N];
int n;
unordered_map p;
int main(){
cin>>n;
while(n--){
int num;
cin>>num;
//分解质因数
for(int i=2;i<=num/i;i++){
while(num%i==0){
num/=i;
p[i]++;
}
}
if(num>1) p[num]++;
}
long long res = 1;
for(auto t : p){
int num = t.first;
int cnt = t.second;
long long a = 1;
while(cnt--){
a = (a * num + 1) % mod;
}
res = res * a % mod;
}
cout< 题目链接:872. 最大公约数 - AcWing题库
思路:G05 最大公约数 欧几里得算法_哔哩哔哩_bilibili
#include
using namespace std;
int gcd(int a,int b){
if(b == 0) return a;
return gcd(b,a%b);
}
int main(){
int n;
cin>>n;
while(n--){
int a,b;
cin>>a>>b;
cout< 欧拉函数
题目链接:873. 欧拉函数 - AcWing题库
思路:欧拉函数表示1-n中与n互质数字的个数。互质就是两个数的最大公约数是1。
解释一下phi(p^k),表示p^(k-1)个循环节,每个循环节中有p-1个数与当前数字互斥。
#include
using namespace std;
long long phi(int n){
long long res = n;
for(int i=2;i<=n/i;i++){
if(n%i==0){
res = res * (i-1)/i;
while(n%i==0) n/=i;
}
}
if(n>1) res = res*(n-1)/n;
return res;
}
int main(){
int n;
cin>>n;
while(n--){
int num;
cin>>num;
cout< 题目链接:874. 筛法求欧拉函数 - AcWing题库
思路:G09 筛法求欧拉函数_哔哩哔哩_bilibili
解释一下为什么i能被p[j]整除,则i包含m(i*p[j])的所有质因子。
参考这篇题解AcWing 874. $\Huge\color{gold}{筛法求欧拉函数}$ - AcWing,如下图所示。由于i与m就相差个p[j],i由m除p[j]得到,所以将i和m分解质因数后可以看出来,i仅在p[j]这个数的次数上相较于m差1,所以说i包含m的所有质因子。
解释一下为什么i不能被p[j]整除的情况下,i与p[j]互质。
因为p[j]是质数,其约数只有1和自身,i不能整除p[j],所以对于i和p[j]来说的最大公约数只有1,所以互质。
#include
using namespace std;
const int N = 1e6+10;
int phi[N],vis[N];
int prime[N],cnt;
void get_phi(int n){
phi[1] = 1;
for(int i=2;i<=n;i++){
if(!vis[i]){
prime[++cnt] = i;
phi[i] = i-1;
}
for(int j=1;i*prime[j]<=n;j++){
int m = i*prime[j];
vis[m] = 1;
if(i%prime[j] == 0){
phi[m] = prime[j]*phi[i];
break;
}
else phi[m] = (prime[j]-1)*phi[i];
}
}
}
int main(){
int n;
cin>>n;
get_phi(n);
long long sum = 0;
for(int i=1;i<=n;i++){
sum+=phi[i];
}
cout< 快速幂
题目链接:875. 快速幂 - AcWing题库
思路:G01 快速幂_哔哩哔哩_bilibili
#include
using namespace std;
typedef long long LL;
LL quickpow(LL a,LL b,LL p){
LL res = 1;
while(b){
if(b&1) res = res * a %p;
a = a*a%p;
b>>=1;
}
return res;
}
int main(){
int n;
cin>>n;
while(n--){
LL a,b,p;
cin>>a>>b>>p;
cout< 题目链接:876. 快速幂求逆元 - AcWing题库
思路:G13 同余式 乘法逆元 费马小定理_哔哩哔哩_bilibili
#include
using namespace std;
typedef long long ll;
ll quick_pow(ll a,ll n,int p){
ll res = 1;
while(n){
if(n&1) res = res * a % p;
a = a * a % p;
n>>=1;
}
return res;
}
int main(){
int n;
cin>>n;
while(n--){
ll a,p;
cin>>a>>p;
if(a%p) cout< 扩展欧几里得算法
题目链接:877. 扩展欧几里得算法 - AcWing题库
思路:G17 不定方程 扩展欧几里得算法_哔哩哔哩_bilibili
#include
using namespace std;
int extra_gcd(int a,int b,int &x,int &y){
if(b==0){
x = 1; y = 0;
return a;
}
int x1,y1;
int d = extra_gcd(b,a%b,x1,y1);
x = y1; y = x1 - a/b*y1;
return d;
}
int main(){
int n;
cin>>n;
while(n--){
int a,b,p;
cin>>a>>b;
int x,y;
extra_gcd(a,b,x,y);
cout< 题目链接:876. 快速幂求逆元 - AcWing题库
思路:使用扩展欧几里得算法求逆元更加通用,快速幂求逆元要求a与p互质,且p为质数。但使用扩展欧几里得算法求逆元只要求a与p互质,不要求p一定为质数。具体思路是将同余式转化为不定方程求解。G18 同余方程 乘法逆元 扩展欧几里得算法_哔哩哔哩_bilibili
#include
using namespace std;
typedef long long ll;
// ll quick_pow(ll a,ll n,int p){
// ll res = 1;
// while(n){
// if(n&1) res = res * a % p;
// a = a * a % p;
// n>>=1;
// }
// return res;
// }
ll extra_gcd(ll a,ll b,ll &x, ll &y){
if(b==0){
x = 1;y=0;
return a;
}
ll x1,y1,d;
d = extra_gcd(b,a%b,x1,y1);
x = y1;y = x1-a/b*y1;
return d;
}
int main(){
int n;
cin>>n;
while(n--){
ll a,p;
ll x,y;
cin>>a>>p;
extra_gcd(a,p,x,y);
if(a%p) cout<<(x%p+p)%p< 题目链接:878. 线性同余方程 - AcWing题库
思路:转化为不定方程求解。G18 同余方程 乘法逆元 扩展欧几里得算法_哔哩哔哩_bilibili
#include
using namespace std;
typedef long long ll;
ll extra_gcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x = 1; y = 0;
return a;
}
ll x1,y1;
ll d = extra_gcd(b,a%b,x1,y1);
x = y1; y = x1-a/b*y1;
return d;
}
int main(){
int n;
cin>>n;
while(n--){
ll a,b,m,x,y;
cin>>a>>b>>m;
ll d = extra_gcd(a,m,x,y);
if(b%d==0){
printf("%lld\n",1ll*b/d*x%m);
}else cout<<"impossible"< 中国剩余定理
题目链接:204. 表达整数的奇怪方式 - AcWing题库
思路:普通的中国剩余定理要求不同的同余方程之间的模互质,扩展中国剩余定理不要求模互质。
G19 中国剩余定理_哔哩哔哩_bilibili
G20 扩展中国剩余定理_哔哩哔哩_bilibili
#include
using namespace std;
typedef long long ll;
const int N = 30;
ll a[30],m[30];
int n;
ll extra_gcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x = 1;y = 0;
return a;
}
ll x1,y1,d;
d = extra_gcd(b,a%b,x1,y1);
x = y1; y = x1 - a/b*y1;
return d;
}
ll CRT(ll m[],ll r[]){
ll m1,m2,r1,r2,p,q;
m1 = m[1],r1 = r[1];
for(int i=2;i<=n;i++){
m2 = m[i];r2 = r[i];
ll d = extra_gcd(m1,m2,p,q);
if((r2-r1)%d) return -1;
p = p*(r2-r1)/d;
p = (p%(m2/d)+m2/d)%(m2/d);
r1 = m1*p+r1;
m1 = m1*m2/d;
}
return (r1%m1+m1)%m1;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i]>>m[i];
}
cout< 高斯消元
题目链接:883. 高斯消元解线性方程组 - AcWing题库
思路:G23 线性方程组 高斯消元法_哔哩哔哩_bilibili
高斯消元法较为繁琐,思路如下图:
高斯-约旦消元法思路较为简单,主要思路是每轮循环,主元所在行不变,主元所在列消成0,如下图:
解的情况如下:
#include
using namespace std;
const int N = 110;
const double eps = 1e-6;
double a[N][N];
int n;
int gauss(){
for(int i=1;i<=n;i++){
int r = i;
for(int j=i;j<=n;j++){
if(fabs(a[j][i])>eps){
r = j;
break;
}
}
if(r!=i) swap(a[i],a[r]);
if(fabs(a[i][i])=i;j--){
a[i][j] = a[i][j] / a[i][i];
}
for(int j=i+1;j<=n;j++){
if(a[j][i]!=0){
for(int k=n+1;k>=i;k--){
a[j][k] -= a[j][i]/a[i][i] *a[i][k];
}
}
}
}
for(int i=n-1;i>=1;i--){
for(int j=i+1;j<=n;j++){
a[i][n+1] -= a[i][j] * a[j][n+1];
}
}
for(int i=1;i<=n;i++){
if(fabs(a[i][i])eps){
r = j;
break;
}
}
if(r!=i) swap(a[i],a[r]);
if(fabs(a[i][i])>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++){
cin>>a[i][j];
}
}
// int rtn = gauss();
int rtn = Gauss_Jordan();
if(rtn == 2){
for(int i=1;i<=n;i++) printf("%.2f\n",a[i][n+1]);
}else if(rtn == 1) cout<<"No solution"< 组合计数
题目链接:885. 求组合数 I - AcWing题库
思路:递推G25 求组合数 递推法 杨辉三角_哔哩哔哩_bilibili
#include
using namespace std;
const int mod = 1e9+7;
const int N = 2010;
int c[N][N];
int main(){
int n;
cin>>n;
for(int i=0;i>a>>b;
cout< 题目链接:AcWing 886. 求组合数 II - AcWing
思路:由于题目数据范围过大,递推法会TLE,可以考虑使用公式法求解,模意义下的组合数不能为小数,分数可以表示为逆元的形式。如何求逆元请看上面快速幂中求逆元的方法,当模数为质数时且ax![]() 1(mod p)中a与p互质(本题中p为很大的质数,a为较小的数,所以a与p一定互质),x表示a的逆元,由费马小定理可得x为a^(p-2)。可以直接用快速幂求取。G26 求组合数 快速幂_哔哩哔哩_bilibili
1(mod p)中a与p互质(本题中p为很大的质数,a为较小的数,所以a与p一定互质),x表示a的逆元,由费马小定理可得x为a^(p-2)。可以直接用快速幂求取。G26 求组合数 快速幂_哔哩哔哩_bilibili
需要注意的是f数组和g数组要定义为long long类型的,不然可能输入的数据会溢出。
#include
using namespace std;
typedef long long ll;
const int N = 1e5+10,mod = 1e9+7;
ll f[N],g[N];
ll quick_pow(ll a,ll n){
ll res = 1;
while(n){
if(n&1) res = res * a % mod;
a = a * a % mod;
n>>=1;
}
return res;
}
int main(){
int n;
cin>>n;
f[0] = 1; g[0] = 1;
for(int i=1;i>a>>b;
// cout< 题目链接:887. 求组合数 III - AcWing题库
思路:当数字a,b远远大于质数p时,则不能保证a与p互质,所以费马小定理不再起作用。可以考虑将a%p映射到0-p-1,使得当前情况转化成上面的情况。G27 求组合数 卢卡斯定理_哔哩哔哩_bilibili
#include
using namespace std;
typedef long long ll;
const int N = 100010;
ll f[N],g[N];
ll quick_pow(ll a,ll n, int p){
ll res = 1;
while(n){
if(n&1) res = res * a % p;
a = a * a % p;
n>>=1;
}
return res;
}
void init(int p){
f[0] = 1; g[0] = 1;
for(int i=1;i>n;
while(n--){
ll a,b,p;
cin>>a>>b>>p;
init(p);
printf("%lld\n",Lucas(a,b,p));
}
return 0;
} 题目链接:888. 求组合数 IV - AcWing题库
思路:G28 求组合数 高精度 线性筛_哔哩哔哩_bilibili
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + ...
3. 用高精度乘法将所有质因子相乘
#include
using namespace std;
typedef long long ll;
const int N = 5010;
int prime[N],cnt;
bool st[N];
void init(){
for(int i=2;i &A,int p){
vector C;
int t = 0;
for(int i=0;i1&&C.back()==0) C.pop_back();
A = C;
}
int main(){
int n,m;
cin>>n>>m;
init();
vector C;
C.push_back(1);
for(int i=1;i<=cnt;i++){
int p = prime[i];
int s = getC(n,m,p);
while(s--) mul(C,p);
}
for(int i=C.size()-1;i>=0;i--) cout< 题目链接:889. 满足条件的01序列 - AcWing题库
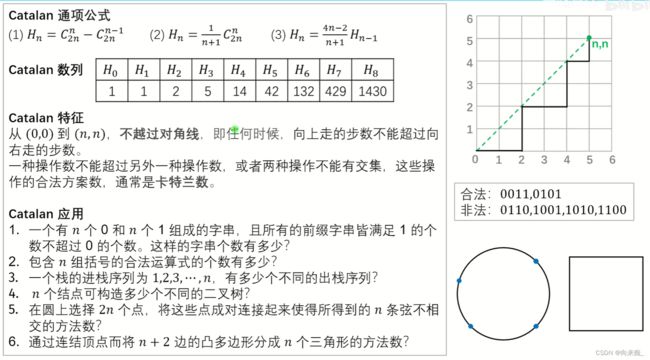
思路:卡特兰数。G32 卡特兰数_哔哩哔哩_bilibili
#include
using namespace std;
const int N = 200010,mod = 1e9+7;
typedef long long ll;
int n;
ll f[N],g[N];
ll qmi(ll a,ll n,int p){
ll res = 1;
while(n){
if(n&1) res = res*a%p;
a= a*a%p;
n>>=1;
}
return res;
}
void init(int p){
f[0] = 1;g[0] = 1;
for(int i=1;i<=2*n+1;i++){
f[i] = f[i-1] * i %p;
g[i] = qmi(i,p-2,p) * g[i-1] % p;
}
}
ll getC(int n,int m,int p){
return f[n] *g[n-m] %p *g[m]%p;
}
int main(){
cin>>n;
init(mod);
cout<<(getC(2*n,n,mod) - getC(2*n,n-1,mod) + mod)%mod< 容斥原理
题目链接:890. 能被整除的数 - AcWing题库
思路:使用2进制位表示当前数字n是否能被每个质数整除。外层循环所有的状态,内层找到每一位G30 容斥原理 集合的并_哔哩哔哩_bilibili
#include
using namespace std;
const int M = 20;
int prim[M];
typedef long long ll;
int main(){
int n,m;
cin>>n>>m;
for(int i=0;i>prim[i];
int res = 0;
for(int i=1;i<1<n){
t = 0;
break;
}
sign = -sign;
t*=prim[j];
}
}
if(t) res = res + n/t*sign;
}
cout< 简单博弈论
题目链接:891. Nim游戏 - AcWing题库
思路:G58 尼姆(Nim)游戏【博弈论】_哔哩哔哩_bilibili
#include
using namespace std;
int main(){
int n;
cin>>n;
int res = 0;
while(n--){
int num;
cin>>num;
res^=num;
}
if(res == 0) cout<<"No"< 题目链接:892. 台阶-Nim游戏 - AcWing题库
思路:G59 台阶型 Nim游戏【博弈论】_哔哩哔哩_bilibili
#include
using namespace std;
const int N = 100010;
int a[N];
int main(){
int n;
cin>>n;
int res = 0;
for(int i=1;i<=n;i++){
cin>>a[i];
if(i%2) res^=a[i];
}
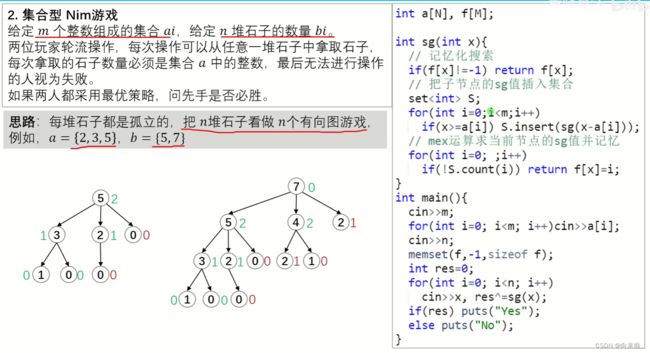
if(res == 0) cout<<"No"< 题目链接:893. 集合-Nim游戏 - AcWing题库
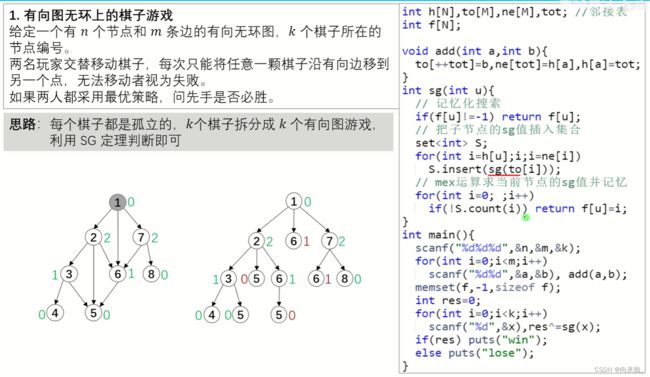
思路:G60 有向图游戏 SG函数【博弈论】_哔哩哔哩_bilibili
#include
using namespace std;
int k,n;
int f[100010];
int a[110];
int sg(int x){
if(f[x]!=-1) return f[x];
set S;
for(int i=0;i=a[i]){
S.insert(sg(x-a[i]));
}
}
for(int i=0;;i++)
if(!S.count(i))
return f[x] = i;
}
int main(){
memset(f,-1,sizeof f);
cin>>k;
for(int i=0;i>a[i];
cin>>n;
int res = 0;
for(int i=0;i>num;
// cout<