代码随想录刷题笔记 DAY 20 | 最大二叉树 No.654 | 合并二叉树 No. 617 | 二叉搜索树中的搜索 No.700 | 验证二叉搜索树 No.98

Day 20

01. 最大二叉树（No. 654）

题目链接

代码随想录题解

1.1 题目

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 *最大二叉树* 。

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

• [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
  • [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
    • 空数组，无子节点。
    • [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
      • 空数组，无子节点。
      • 只有一个元素，所以子节点是一个值为 1 的节点。
  • [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
    • 只有一个元素，所以子节点是一个值为 0 的节点。
    • 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• nums 中的所有整数 互不相同

1.2 笔记

力扣只提供了一个构造的方法，但没有告知这个最大二叉树到底是什么

最大二叉树指的是给出一个 数组，先选取数组中的 最大 的元素作为根节点，根节点左边为左子树，右边为右子树，再分别对左子树和右子树的数组做相同的操作，直到遍历完成。

这道题目和昨天的一道题目思想非常类似，都是构造二叉树的题目

代码随想录刷题笔记 DAY 18 | 找树左下角的值 No.513 | 路经总和 No.112 | 从中序与后序遍历序列构造二叉树 No.106

中的 03.从中序与后序遍历序列构造二叉树（No. 106）

这里给出一个基本的思路和实现方式，首先看实现这个方法要执行的操作

1. 在数组中找到最大的元素
2. 以这个元素为节点分割左子树和右子树
3. 左子树执行相同的操作
4. 右子树执行相同的操作
5. 将节点返回

显然是要通过递归来完成，将下一个方法执行的结果作为返回值返回给该方法。

提到递归显然就要考虑递归的三个要考虑到的部分

• 递归的出口：因为因为传入的是一个数组，所以递归的出口就是 nums == null 或者 nums.length == 0，也就是数组为空的情况
• 数组的返回值：通过上面的步骤明确我们要从下个函数拿到什么，显然是要拿到这个节点的左子树和右子树，所以返回值就是一个 TreeNode
• 递归重要执行的步骤：找到最大的元素、分割数组、遍历左节点和右节点

找到最大的节点可以封装为一个方法，因为不止要找到这个数组中最大的元素还需要得到数组中的下标，所以重新封装一个对象作为返回值，返回值中包括下标和大小（也可以只返回下标），为了代码整洁这里再封装一个对象

/**
    作为方法的返回值，返回节点的值和在数组中的下标
 */
class NodeMessage {
    int val;
    int index;
    public NodeMessage(int val, int index) {
        this.val =val;
        this.index = index;
    }
}

找到最大值的方法：

    /**
        返回当前数组中最大的数字和下标
     */
public NodeMessage getMaxNumAndIndex(int[] nums) {
        int tempIndex = 0;
        int tempMax = nums[0];
        for (int i = 0; i < nums.length; i++) {
            if (tempMax < nums[i]) {
                tempMax = nums[i];
                tempIndex = i;
            }
        }
        return new NodeMessage(tempMax, tempIndex);
	}
}

1.3 代码

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return reverse(nums);
    }
    public TreeNode reverse(int[] nums) {
        if (nums.length == 0 || nums == null) {
            return null;
        }
        NodeMessage nodeMessage = getMaxNumAndIndex(nums); // 获得最大值作为当前的节点
        int[] left = Arrays.copyOfRange(nums, 0, nodeMessage.index);
        int[] right = Arrays.copyOfRange(nums, (nodeMessage.index+1), nums.length);
        TreeNode node = new TreeNode(nodeMessage.val);
        node.left = reverse(left);
        node.right = reverse(right);
        return node;
    }
    /**
        返回当前数组中最大的数字和下标
     */
    public NodeMessage getMaxNumAndIndex(int[] nums) {
        int tempIndex = 0;
        int tempMax = nums[0];
        for (int i = 0; i < nums.length; i++) {
            if (tempMax < nums[i]) {
                tempMax = nums[i];
                tempIndex = i;
            }
        }
        return new NodeMessage(tempMax, tempIndex);
    }
}
/**
    作为方法的返回值，返回节点的值和在数组中的下标
 */
class NodeMessage {
    int val;
    int index;
    public NodeMessage(int val, int index) {
        this.val =val;
        this.index = index;
    }
}

1.4 补充

同样的，重复的切割数组的操作会导致运行时间很长，所以可以采用虚拟切割的方法，通过传入数组的起始位置和终止位置来限制对原数组的访问来达到切割的效果，这里直接给出代码。

class Solution {
    int[] globalNums;
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        globalNums = nums;
        return reverse(0, globalNums.length-1);
    }
    public TreeNode reverse(int startIndex, int endIndex) {
        if (startIndex > endIndex) {
            return null;
        }
        int index = getIndex(startIndex, endIndex); // 获得最大值作为当前的节点
        int leftStartIndex = startIndex;
        int leftEndIndex = index - 1;
        int rightStartIndex = index + 1;
        int rightEndIndex = endIndex;
        TreeNode node = new TreeNode(globalNums[index]);
        node.left = reverse(leftStartIndex, leftEndIndex);
        node.right = reverse(rightStartIndex, rightEndIndex);
        return node;
    }
    /**
        返回当前数组中最大的数字和下标
     */
    public int getIndex(int startIndex, int endIndex) {
        int tempIndex = startIndex;
        for (int i = startIndex; i <= endIndex; i++) {
            if (globalNums[tempIndex] < globalNums[i]) {
                tempIndex = i;
            }
        }
        return tempIndex;
    }
}

02. 合并二叉树（No. 617）

题目链接

代码随想录题解

2.1 题目

给你两棵二叉树： root1 和 root2 。

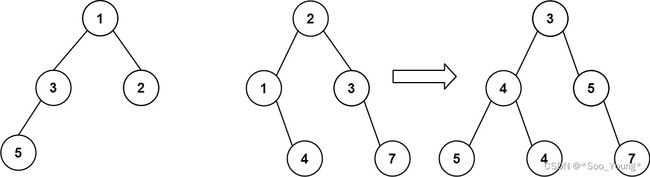
想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内
• -104 <= Node.val <= 104

2.2 笔记

这道题的难点其实是处理两个二叉树，但是和之前的题目相同的是，无论是处理几个二叉树，其前序、中序和后序位置是相同的，仍然可以按照之前的思路去处理这些问题。

这道题采用递归的方式解题，继续来思考递归的三个要考虑的部分：

• 递归的返回值，这道题其实还是遍历构造二叉树，所以返回值仍然是 TreeNode ，在每次递归中构造新的节点传给上一个节点作为子树。
• 递归的终止条件：root1 == null 或者 root2 == null
• 每次递归中要做的事情：首先判断是否遍历到空节点，上面提到返回的节点是作为上一个节点的子树，对于遍历到 root1 为空就应该返回 root2 作为子树，遍历到 root2 为空就应该将 root1 作为子树，这样就完成了题目中的对 null 的处理（其实上面已经包含了 root1 == null && root2 == null 的部分了，因为当这个情况其实是直接返回 null），如果对于节点都存在的情况，返回的节点就是 new TreeNode(root1.val + root2.val)

这样就能写出代码

2.3 代码

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return reverse(root1, root2);
    }
    public TreeNode reverse(TreeNode root1, TreeNode root2) {
        if (root1 == null) {
            return root2;
        }
        if (root2 == null) {
            return root1;
        }
        TreeNode node = new TreeNode(root1.val + root2.val);
        node.left = reverse(root1.left, root2.left);
        node.right = reverse(root1.right, root2.right);
        return node;
    }
}

03. 二叉搜索树中的搜索（No. 700）

题目链接

代码随想录题解

3.1 题目

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

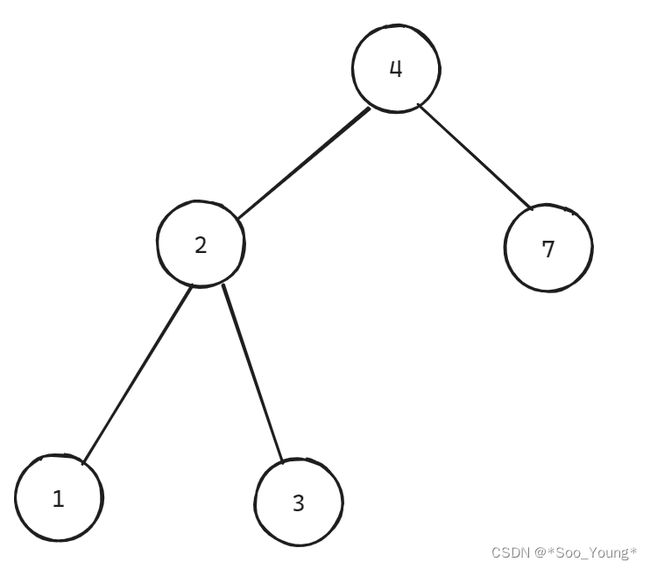
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 树中节点数在 [1, 5000] 范围内
• 1 <= Node.val <= 107
• root 是二叉搜索树
• 1 <= val <= 107

3.2 笔记

本题主要是考察对二叉搜索树的概念的掌握

即使刷了很多的算法题，也不要忘记数据结构最重要的任务是 存储数据，说白了就是增删改查，二叉搜索树就是存储数据的一种方式，一组数据，先选择一个节点作为根节点（最好保证左右均匀），将小于根节点的置于左子树，大于的置于右子树，往下每次都是这样：选择节点、大的放在左子树，小的放在右子树，直到数组中没有元素，就构建了二叉搜索树。

这样存放的好处就是将搜索时间大大减小了，将搜索速度从 n 变为了 log n（最好的情况），所谓最好的情况就是每次都能排除一半的节点（平衡二叉树），最坏的情况就还是 n，但是如果安排的好那二叉搜索树就会大大降低搜索的时间。

所以遍历的时候看当前节点的值是比需要的大还是小，如果大就去遍历左子树，反之则取遍历右子树，直到 node == null 的时候，说明没有找到，或者 node.val == val 的时候说明找到了。

3.3 代码

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        return reverse(root, val);
    }
    public TreeNode reverse(TreeNode root, int val) {
        if (root == null) {
            return null;
        }
        if (root.val > val) {
            return reverse(root.left, val);
        } else if (root.val < val) {
            return reverse(root.right, val);
        } else if (root.val == val) {
            return root;
        }
        return null;
    }
}

04. 验证二叉搜索树（No. 98）

题目链接

代码随想录题解

4.1 题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

4.2 笔记

要验证二叉搜索树就需要用到它关键的性质：

中序遍历遍历出来的列表是有序的

这是因为二叉搜索树是左子树小于中间节点而右子树大于中间节点，中序遍历又恰好是左中右的顺序，所以得到的序列的是有序的。

很容易就能想出一种解题方法：

通过中序遍历得到一个列表，再在主方法中去验证这个列表是否是有序的，很容易的写出代码

    public void reverse(TreeNode node) {
        if (node == null) {
            return;
        }
        reverse(node.left);
        nums.add(new Long(node.val));
        reverse(node.right);
    }

这样得到的列表就是一个有序列表（如果是二叉搜索树的话），后面就是验证这个列表有序了

列表有序就是后一个一定大于前面的值所有，前面的所有可以用前面所有数值的最大值来代表，就是 maxValue，设定 maxValue = Long.MIN-VALUE，遍历这个数组

        for (Long i : nums) {
            if (i > temp) {
                temp = i;
            } else {
                return false;
            }
        }

判断后面的是否比前面的要大，如果发现后面有值小于等于 maxValue 则说明数组不是有序的

完整的代码在下一小节

除了将其抽离出一个数组，是否可以在遍历的途中去执行上面的操作呢？

肯定是可以的，但是递归要比直接去遍历难理解一些，先来看下面的代码

public void reverse(Treenode node) {
	reverse(node.left);
	System.out.println(node.val);
	reverse(node.right);
}

上面的代码会输出什么呢？

答案非常简单，就是上面的有序的数组，那把上面的对数组判断的代码直接移动到中序位置不就是可以判断了吗？

理一下递归的三个要考虑的部分

• 递归的出口：node == null
• 递归的返回值：这里直接返回它是否是一个二叉搜索树，所以要去验证左子树和右子树，该节点满足条件其实就是左节点和右节点是否同时满足情况；搞懂返回值是什么，return 的时候就不会迷糊了
• 递归中要进行的步骤：判断是否符合出口情况、递归左子树、通过上面的方法查看是否有序、递归右子树、返回

很容易可以写出代码

1.3 代码

直接思路

class Solution {
    List<Long> nums = new ArrayList<>();
    public boolean isValidBST(TreeNode root) {
        if (root == null || root.right == null && root.left == null) {
            return true;
        }
        reverse(root);
        Long temp = Long.MIN_VALUE;
        for (Long i : nums) {
            if (i > temp) {
                temp = i;
            } else {
                return false;
            }
        }
        return true;
    }
    public void reverse(TreeNode node) {
        if (node == null) {
            return;
        }
        reverse(node.left);
        nums.add(new Long(node.val));
        reverse(node.right);
    }
}

递归优化

class Solution {
    List<Long> nums = new ArrayList<>();
    public boolean isValidBST(TreeNode root) {
        if (root == null || root.right == null && root.left == null) {
            return true;
        }
        return reverse(root);
    }
    Long max_value = Long.MIN_VALUE;
    public boolean reverse(TreeNode node) {
        if (node == null) {
            return true;
        }
        boolean leftBol = reverse(node.left);
        if (node.val > max_value) {
            max_value = new Long(node.val);
        } else {
            return false;
        }
        boolean rightBol = reverse(node.right);
        return leftBol && rightBol;
    }
}