ST表（保姆级，简单易懂）

介绍

ST表（Sparse Table）是一种用于高效处理区间查询的数据结构。它可以在O(1)的时间复杂度内回答某一区间的最值查询（最小值、最大值等）。ST表使用动态规划的思想，通过预处理的方式来快速计算出各个区间的最值。

引入

假设有8个数据，如何找出极差？

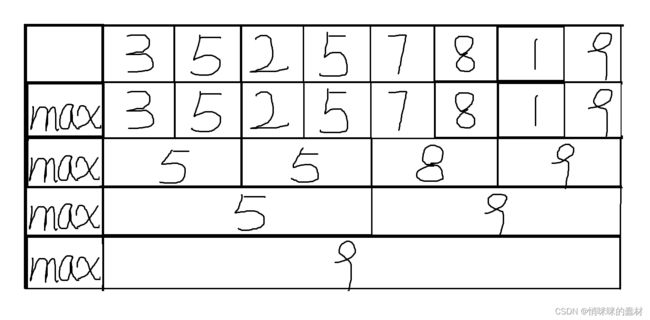
例：3 5 2 5 7 8 1 9

通过部分区间的最值推导出整个区间的最值，同样我们可以求出最小值1，极差就是8。

这个操作我们可以逆向考虑，将区间一分为二，要找出3 5 2 5和7 8 1 9的最值就需要找出 3 5，2 5，7 8 ，1 9的最值。

那么我们可以对一个包含2^j的数字的区间[i，i+2^j-1]（注意要减1，可以举例子理解）进行维护。

将区间一分为二，因为数据是离散的，所以端点我们要考虑一下。可以得出，第一个区间以i为起点，包含2^(j-1)个数，第二个区间以i+2^(j-1)为起点，包含2^(j-1)个数。总包含2^j个数（不明白可以举例，如1 2 3 4）

建表

定义st[i][j]为以i为起点，包含2^j个数的区间。由引入部分的图解，我们可以写出递推式

st[i][j] = max (st[i][j - 1] , st[i + (1 << j - 1)][j - 1]);
//i << j - 1 就是 2 ^ (j - 1),代码一定要这么写。 

因为递推需要知道子区间的最值，最小子区间就是单个数字，也就是st[i][0],所以需要先对st[i][0]赋初始值。然后从j=1开始，枚举所有包含2^j个数字的区间。代码如下

for (int i = 1; i <= n; i++)  cin >> stmax[i][0];
for (int j = 1; (1 << j) <= n; j++)//总包含数字不超过n
	{
		for (int i = 1; i + (1 << j) - 1 <= n; i++)//确保是子区间，不越界
		{
			stmin[i][j] = min(stmin[i][j - 1], stmin[i + (1 << j - 1)][j - 1]);
			stmax[i][j] = max(stmax[i][j - 1], stmax[i + (1 << j - 1)][j - 1]);
		}
	}

查表 

定义两个变量l,r为查找区间的左右端点。要查区间的最值，只需分别查如图两段包含2^x个数的区间的最值，再进行比较，就得到所查区间的最值。为此，我们必须保证，两端区间必须包含了所有所查区间的数。因此我们需要得出最大的x。2^x<2^j即2^x,得出x,x最大就向下取整。两端区间的端点分别是l和r-(1<

代码如下

int l, r;
cin >> l >> r;
int x = log_2[r - l + 1];
cout << max(st[l][x], st[r - (1 << x) + 1][x] << endl;

log2向下取整函数自己写即可,在下面题目的代码中，自行消化。

水题一道熟练一下

代码如下：

#include
using namespace std;
int n, q;
const int MAXN = 5e4+5,MAX_L = 20;
int log_2[MAXN];
int stmin[MAXN][MAX_L];
int stmax[MAXN][MAX_L];

int main()
{
	cin >> n >> q;
	log_2[0] = -1;
	for (int i = 1; i <= n; i++)
	{
		cin >> stmax[i][0];
		stmin[i][0] = stmax[i][0];
		log_2[i] = log_2[i >> 1] + 1;
	}
	for (int j = 1; (1 << j) <= n; j++)
	{
		for (int i = 1; i + (1 << j) - 1 <= n; i++)
		{
			stmin[i][j] = min(stmin[i][j - 1], stmin[i + (1 << j - 1)][j - 1]);
			stmax[i][j] = max(stmax[i][j - 1], stmax[i + (1 << j - 1)][j - 1]);
		}
	}
	while(q--)
	{
		int l, r;
		cin >> l >> r;
		int x = log_2[r - l + 1];
		cout << max(stmax[l][x], stmax[r - (1 << x) + 1][x]) - min(stmin[l][x], stmin[r - (1 << x) + 1][x]) << endl;
	}
}

感谢阅读~