Java八大常用排序算法
1冒泡排序
对于冒泡排序相信我们都比较熟悉了,其核心思想就是相邻元素两两比较,把较大的元素放到后面,在一轮比较完成之后,最大的元素就位于最后一个位置了,就好像是气泡,慢慢的浮出了水面一样
Jave 实现
public class BubbleSort1 {
public static void BubbleSort(int[] arr) {
for(int i=0;i冒泡排序算法还是比较好理解的,只需要进行两次循环,最外层的循环代表排序元素的个数,内部循环则进行两两比较,时间复杂度为 O(n^2)
2快速排序
快排的思想为首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序,之后再递归排序两边的数据
Jave 实现
public class QuickSort {
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return;
}
i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i=arr[i]&&i 相比冒泡排序,快速排序每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了,时间复杂度为 O(N*logN)
3直接插入排序
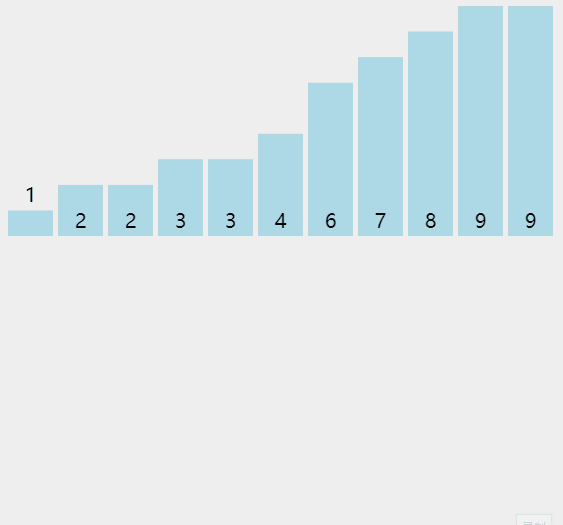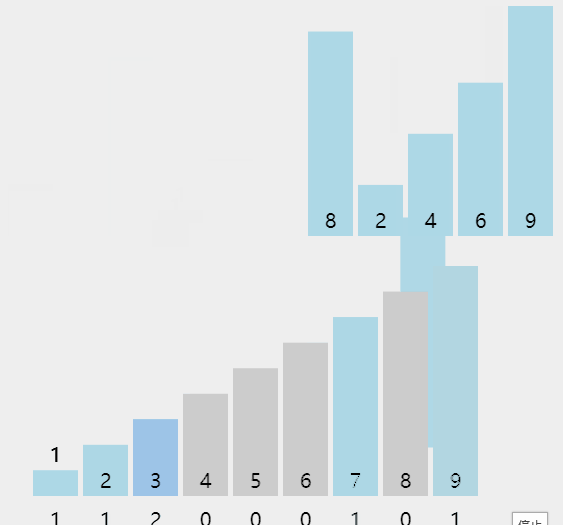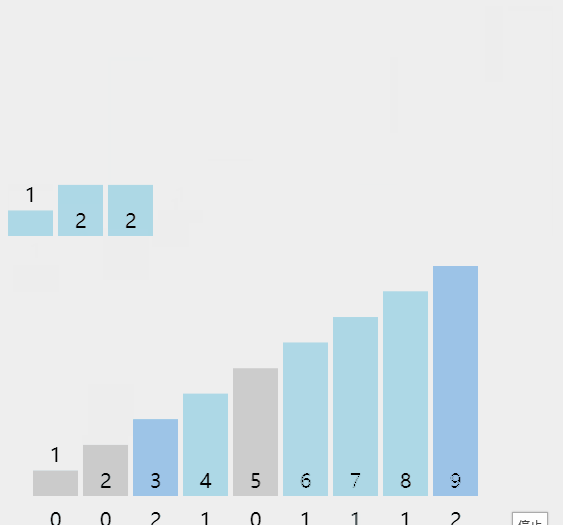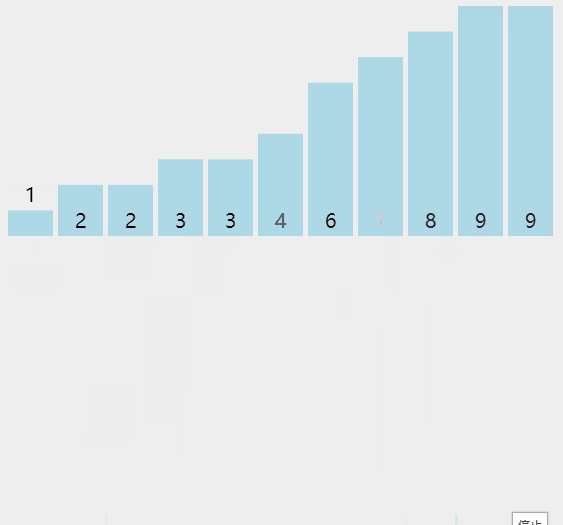
插入排序的思想是把一个数据插入到一个有序序列中,从而得到一个新的序列加一的有序序列,可以通过下图来进一步加深理解
Java 实现
public static void InsertSort(int[] arr)
{
int i, j;
int n = arr.Length;
int target;
//假定第一个元素被放到了正确的位置上
//这样,仅需遍历1 - n-1
for (i = 1; i < n; i++)
{
j = i;
target = arr[i];
while (j > 0 && target < arr[j - 1])
{
arr[j] = arr[j - 1];
j--;
}
arr[j] = target;
}
}
由于每次遍历有序序列时,都会有序列中所有的数据做对比,故而时间复杂度为O(n^2)
4选择排序
选择排序,是逐个确定元素位置的思想。同样是 n 遍循环,第一轮时,每一个元素都与第一个元素比较,如果比第一个元素大,则与之交换,这样一轮过后,第一个元素就是最小的了,第二轮开始每个元素与第二个位置的元素比较,如果大,则与第二位置的元素交换,以此类推,达到排序的目的
Java 实现
public static int[] selectionSort(int[] array) {
int len = array.length;
// 如果数组长度为0或者1,都是不用排序直接返回
if(len == 0 || len == 1) {
return array;
}
for(int i = 0; i < len - 1; i++) {
int minIdx = i;
for(int j = i + 1; j < len; j++) {
// 找到最小的数
if(array[minIdx] > array[j]) {
// 保存最小数的索引
minIdx = j;
}
}
// 如果一轮比较下来都没有变更最小值的索引则无需调换顺序
if(minIdx != i) {
int tmp = array[i];
array[i] = array[minIdx];
array[minIdx] = tmp;
}
}
return array;
}
选择排序和冒泡排序还是很相似的,但是选择排序会比冒泡排序少一次交换的过程,但是同样是两层循环,所有时间复杂度也是 O(n^2)
5并归排序
可以把一个数组分成两半,对于每一个数组当他们是有序的就可以进行一次合并操作。对于他们的两个区间进行递归,一直递归下去划分区间,当区间只有一个值的时候我们就可以进行合并返回上一层,让上一层合并再返回
Java 实现
public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2;
if(low归并排序采用分而治之的原理:首先将一个序列从中间位置分成两个序列,然后再将这两个子序列按照第一步继续二分下去,最后直到所有子序列的长度都为1,也就是不可以再二分截止。这时候再两两合并成一个有序序列即可。时间复杂度 O(NlogN)
6随机快速排序
随机快速排序与快速排序的思路一样,差异就是取主元之前,随机快速排序多了一个步骤:随机快速排序是随机取得一个元素,并且会与最后一个元素交换位置。取得主元的下标位置实际上还是最后一个下标,快速排序是习惯取得最后一个元素作为主元
Java 实现
package quicksort;
import java.util.Random;
public class RandomQuickSort {
public void Sort(int[] a, int p, int r) {
if (p < r) {
int q = Partition(a, p, r);
Sort(a, p, q-1);
Sort(a,q+1, r);
}
}
private int Partition(int[] A, int p, int r) {
/*随机选取主元元素*/
Random random = new Random();
int random_index = random.nextInt(r-p+1)+p;
System.out.println("random_index="+random_index);
int temp = A[random_index];
A[random_index] = A[r];
A[r] = temp;
int x = A[r]; //pivot = A[p]
int i = p-1;
for (int j = p; j < r; j++) {
if (A[j] <= x) { //与pivot作比较
i++;
int tmp = A[j];
A[j] = A[i];
A[i] = tmp;
}
}
int tmp = A[r];
A[r] = A[i+1];
A[i+1] = tmp;
return i+1;
}
}7计数排序
首先统计原数组中每个值出现的次数
然后进行排序:遍历Count数组,对应位置的值出现多少次就往原数组写几个这个值
当然,在对于数据比较大的时候我们可以通过相对映射,让(该值-min)后的数组加一,最后还原回去即可
Java 实现
public static int[] CountingSort(int[] a) {
int b[] = new int[a.length];
int max = a[0], min = a[0];
for (int i=1;i max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
// k的大小是要排序的数组中,元素大小的极值差+1
int k = max - min + 1;
int c[] = new int[k];
//统计A数组元素出现次数
for (int i = 0; i < a.length; ++i) {
c[a[i] - min] += 1;
}
//更新计算C数组
for (int i = 1; i < c.length; ++i) {
c[i] = c[i] + c[i - 1];
}
//填充B数组
for (int i = a.length - 1; i >= 0; --i) {
b[--c[a[i] - min]] = a[i];
}
return b;
}
8基数排序
基数排序核心思想是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前
Java 版实现
public class RadixSort {
public static void main(String[] args) {
int[] arr = {63, 157, 189, 51, 101, 47, 141, 121, 157, 156,
194, 117, 98, 139, 67, 133, 181, 12, 28, 0, 109};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
/**
* 高位优先法
*
* @param arr 待排序列,必须为自然数
*/
private static void radixSort(int[] arr) {
//待排序列最大值
int max = arr[0];
int exp;//指数
//计算最大值
for (int anArr : arr) {
if (anArr > max) {
max = anArr;
}
}
//从个位开始,对数组进行排序
for (exp = 1; max / exp > 0; exp *= 10) {
//存储待排元素的临时数组
int[] temp = new int[arr.length];
//分桶个数
int[] buckets = new int[10];
//将数据出现的次数存储在buckets中
for (int value : arr) {
//(value / exp) % 10 :value的最底位(个位)
buckets[(value / exp) % 10]++;
}
//更改buckets[i],
for (int i = 1; i < 10; i++) {
buckets[i] += buckets[i - 1];
}
//将数据存储到临时数组temp中
for (int i = arr.length - 1; i >= 0; i--) {
temp[buckets[(arr[i] / exp) % 10] - 1] = arr[i];
buckets[(arr[i] / exp) % 10]--;
}
//将有序元素temp赋给arr
System.arraycopy(temp, 0, arr, 0, arr.length);
}
}
}