Python数据分析及可视化实例之“NumPy“
一、概述
什么是Numpy:Numeric Python ?
NumPy系统是Python的一种开源的数值计算扩展
一个强大的N维数组对象Array
比较成熟的(广播)函数库
用于整合C/C++和Fortran代码的工具包
实用的线性代数、傅里叶变换和随机数生成函数
numpy和稀疏矩阵运算包scipy配合使用更加强大
二、Numpy安装与版本确认
安装
安装 NumPy 最简单的方法就是使用 pip工具:(不建议使用)
pip3 install --user numpy scipy matplotlib
--user 选项可以设置只安装在当前的用户下,而不是写入到系统目录。
默认情况使用国外线路,国外太慢,我们使用清华的镜像就可以:
pip3 install numpy scipy matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple
测试是否安装成功:
In[ ]:
from numpy import *
eye(4)
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
导入numpy与版本确认(numpy get started)
In[ ]:
import numpy as np
#查看版本
np.__version__
'1.19.5'
三、NumPy
NumPy之Ndarray 对象
NumPy 最重要的一个特点是其N维数组对象 ndarray,它是一系列同类型数据的集合,以0下标为开始进行集合中元素的索引。
ndarray 对象是用于存放同类型元素的多维数组。(如果传进来的列表中包含不同的类型,则统一为同一类型,优先级:str > float > int)
ndarray 中的每个元素在内存中都有相同存储大小的区域。
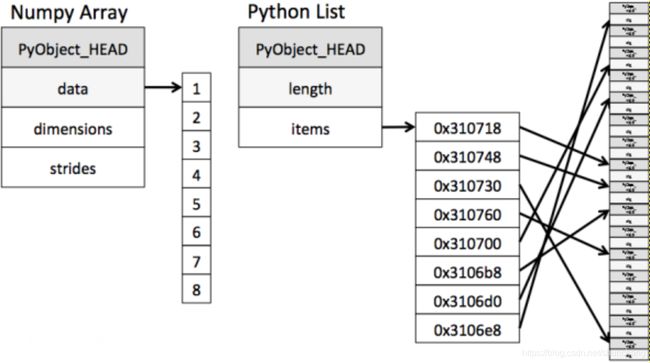
ndarray 内部由以下内容组成:
一个指向数据(内存或内存映射文件中的一块数据)的指针。
数据类型或 dtype,描述在数组中的固定大小值的格子。
一个表示数组形状(shape)的元组,表示各维度大小的元组。
一个跨度元组(stride),其中的整数指的是为了前进到当前维度下一个元素需要"跨过"的字节数。
ndarray 的内部结构:
跨度可以是负数,这样会使数组在内存中后向移动,切片中 obj[::-1] 或 obj[:,::-1] 就是如此。
创建一个 ndarray 只需调用 NumPy 的 array 函数即可:
numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)
参数说明:
| 名称 |
描述 |
| object |
数组或嵌套的数列 |
| dtype |
数组元素的数据类型,可选 |
| copy |
对象是否需要复制,可选 |
| order |
创建数组的样式,C为行方向,F为列方向,A为任意方向(默认) |
| subok |
默认返回一个与基类类型一致的数组 |
| ndmin |
指定生成数组的最小维度 |
一、创建ndarray
1. 使用np.array()由python list创建
注意:
- numpy默认ndarray的所有元素的类型是相同的
- 如果传进来的列表中包含不同的类型,则统一为同一类型,优先级:str>float>int
In[ ]:
l = [3,1,4,5,9,6] #一维的数组
n = np.array(l)
display(n,l)
array([3, 1, 4, 5, 9, 6])
[3, 1, 4, 5, 9, 6]
In[ ]:
# 多于一个维度
import numpy as np
a = np.array([[1, 2], [3, 4]])
print (a)
[[1 2]
[3 4]]
In[ ]:
# 最小维度
import numpy as np
a = np.array([1,2,3,4,5], ndmin = 2)
print (a)
[[1 2 3 4 5]]
In[ ]:
# dtype 参数
import numpy as np
a = np.array([1, 2, 3], dtype = complex)
print (a)
[1.+0.j 2.+0.j 3.+0.j]
如果要确定,数组的维度,使用np.shape方法(翻译:shape,形状)
In[ ]:
l = [3,1,4,5,9,6]
n = np.array(l) #shape()是数组的属性,需要把集合变成数组,然后np.shape
display(n.shape)
(6,)
In[ ]:
n2 = np.array([[3,4,7,1],[3,0,1,8],[2,4,6,8]])
display(n2.shape)
(3, 4)
对于数组中有不同类型的元素,则会将元素统一为同一类型
In[ ]:
n3 = np.array(['0',9.18,20])
n3
array(['0', '9.18', '20'], dtype='
2. 使用np的routines函数创建
包含以下常见创建方法:
- np.ones(shape, dtype=None, order='C')
参数说明:
用“1”来填充一个矩阵:
shape:形状,生成2行3列矩阵:shape=(2,3);
dtype:指的是数组当中数据元素的类型,如果单type,指的是整个对象的类型;默认类型是numpy.float64
order:影响数组在内存中的储存方式,不用动;('C' 用于 C 的行数组,或者 'F' 用于 FORTRAN 的列数组)
In[ ]:
one = np.ones((2,3,5),dtype=int)
one
array([[[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]],
[[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]]])
In[ ]:
# 自定义类型
np.ones([3,3],dtype=int)
array([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]])
In[ ]:
import matplotlib.pyplot as plt #图片需要导入matplotlib.pyplot
ones = np.ones(shape = (100,80,3),dtype=float)
plt.imshow(ones) #imshow是matlab中显示图像的函数,imshow(BW) 功能,显示一张二值图像BW,负责对图像进行处理,并显示其格式,但是不能显示!
plt.show #显示出来
2) np.zeros(shape, dtype=float, order='C')
返回来一个给定形状和类型的用0填充的数组;
In[ ]:
np.zeros((2,3,5))
array([[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]],
[[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]]])
3) np.full(shape, fill_value, dtype=None, order='C')
返回给定维度和类型的新数组,填充 fill_value。
shape:形状:整数或整数序列新数组的形状,例如(2,3)或2;
fill_value: 填充值;
dtype:返回数组的数据类型;
order:在计算机内存中的存储元素的顺序,只支持 ‘C’(按行)、‘F’(按列),默认 ‘C’;
In[ ]:
np.full((2,3),fill_value=8.88)
array([[8.88, 8.88, 8.88],
[8.88, 8.88, 8.88]])
4) np.eye(N, M=None, k=0, dtype=float)
对角线为1其他的位置为0
生成对角矩阵;
N:列数
M:行数
K:默认情况下输出的是对角线全“1”,其余全“0”的方阵,如果k为正整数,则在右上方第k条对角线全“1”其余全“0”,k为负整数则在左下方第k条对角线全“1”其余全“0”。对角线的偏移量。
In[ ]:
#矩阵,满秩矩阵
np.eye(5)
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
5) np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
在指定的间隔内返回均匀间隔的
start:序列的起始值
stop:序列的终止值
num:采样的数目,默认值为50
dtype:输出序列的类型
In[ ]:
# lin = linear 线性
# 00000000
# 11111111 = 127
np.linspace(start = 0,stop = 150,num = 50,endpoint=False,retstep=True,dtype=np.int8)
(array([ 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30,
33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63,
66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96,
99, 102, 105, 108, 111, 114, 117, 120, 123, 126, -127,
-124, -121, -118, -115, -112, -109], dtype=int8),
3.0)
In[ ]:
np.linspace(start = 0,stop = 150,num = 50)
array([ 0. , 3.06122449, 6.12244898, 9.18367347,
12.24489796, 15.30612245, 18.36734694, 21.42857143,
24.48979592, 27.55102041, 30.6122449 , 33.67346939,
36.73469388, 39.79591837, 42.85714286, 45.91836735,
48.97959184, 52.04081633, 55.10204082, 58.16326531,
61.2244898 , 64.28571429, 67.34693878, 70.40816327,
73.46938776, 76.53061224, 79.59183673, 82.65306122,
85.71428571, 88.7755102 , 91.83673469, 94.89795918,
97.95918367, 101.02040816, 104.08163265, 107.14285714,
110.20408163, 113.26530612, 116.32653061, 119.3877551 ,
122.44897959, 125.51020408, 128.57142857, 131.63265306,
134.69387755, 137.75510204, 140.81632653, 143.87755102,
146.93877551, 150. ])
6) np.arange([start, ]stop, [step, ]dtype=None)
在给定间隔内返回均匀间隔的值。值在半开区间 [开始,停止]内生成(换句话说,包括开始但不包括停止的区间),返回的是 ndarray 。
start —— 开始位置,数字,可选项,默认起始值为0
stop —— 停止位置,数字
step —— 步长,数字,可选项, 默认步长为1,如果指定了step,则还必须给出start。
dtype —— 输出数组的类型。 如果未给出dtype,则从其他输入参数推断数据类型。
返回:
arange:ndarray
均匀间隔值的数组。
注意:对于浮点参数(参数为浮点),结果的长度为ceil((stop - start)/ step)) 由于浮点溢出,此规则可能导致最后一个元素大于stop。因此要特别注意
In[ ]:
np.arange(0,100,step = 3)
array([ 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48,
51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99])
7) np.random.randint(low, high=None, size=None, dtype='l')
low—–为最小值
high—-为最大值
size—–为数组维度大小
dtype—为数据类型,默认的数据类型是np.int。
返回值:
返回随机整数或整型数组,范围区间为[low,high),包含low,不包含high;
high没有填写时,默认生成随机数的范围是[0,low),随机生成区间内的一个整数。
In[ ]:
#ndarray
np.random.randint(-100,100,size = (4,5))
array([[-21, 95, -92, -82, 18],
[ -4, -58, -85, 0, 93],
[-52, 24, -44, 94, 14],
[ 24, -42, 11, -6, -11]])
8) np.random.randn(d0, d1, ..., dn)
标准正太分布
rand函数根据给定维度生成[0,1)之间的数据,包含0,不包含1
dn表格每个维度
返回值为指定维度的array
In[ ]:
#d0,d1……dn
#dimensional 维度
np.random.randn(2,2)
array([[ 2.9323179 , -0.52229644],
[-1.57196274, -0.7304904 ]])
9) np.random.normal(loc=0.0, scale=1.0, size=None)
普通正态分布
loc:float;此概率分布的均值(对应着整个分布的中心centre)
scale:float;此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)
size:int or tuple of ints;输出的shape,默认为None,只输出一个值
In[ ]:
np.random.normal(175,100,56)
array([132.44700835, 124.88970839, 207.91759326, 274.91459194,
289.78342744, 316.84093516, 68.30847232, 87.22738987,
189.69581369, 173.234369 , 14.17717944, 218.68074211,
214.76200606, 359.01632704, 211.25431991, 48.06710547,
220.03881157, 176.07973654, 174.2790892 , 63.5676417 ,
204.79259998, 359.1096867 , 128.47983432, 131.99724887,
260.63815625, 266.31307691, 268.23095105, 143.55945709,
356.7349408 , 55.49789815, 62.9268791 , 307.36801101,
124.25949273, 122.28770555, 153.04858479, 304.3048676 ,
89.62540276, 218.50123029, 284.95636614, 226.81144485,
160.04816989, 238.90494062, 18.31975515, 114.71202492,
142.25181009, 232.56186049, 154.73708967, 265.10839932,
186.96409292, 219.92183863, 227.69860028, 174.5008949 ,
161.27998806, 236.44246104, 183.47538765, 290.4305708 ])
10) np.random.random(size=None)
生成0到1的随机数,左闭右开
In[ ]:
np.random.random(size = 10)
array([0.3572361 , 0.55457738, 0.25533856, 0.42303569, 0.72208673,
0.95651551, 0.49013416, 0.60802548, 0.92484268, 0.45199402])
扩展:
#使用随机数成成一张图片
In[ ]:
image = np.random.random(size = (10,20,3))
plt.imshow(image)
plt.show()
二、ndarray的属性
NumPy 数组的维数称为秩(rank),秩就是轴的数量,即数组的维度,一维数组的秩为 1,二维数组的秩为 2,以此类推。
在 NumPy中,每一个线性的数组称为是一个轴(axis),也就是维度(dimensions)。比如说,二维数组相当于是两个一维数组,其中第一个一维数组中每个元素又是一个一维数组。所以一维数组就是 NumPy 中的轴(axis),第一个轴相当于是底层数组,第二个轴是底层数组里的数组。而轴的数量——秩,就是数组的维数。
很多时候可以声明 axis。
axis=0,表示沿着第 0 轴进行操作,即对每一列进行操作;axis=1,表示沿着第1轴进行操作,即对每一行进行操作。
NumPy 的数组中比较重要 ndarray 对象属性有:
| 属性 |
说明 |
| ndarray.ndim |
秩,即轴的数量或维度的数量 |
| ndarray.shape |
数组的维度,对于矩阵,n 行 m 列 |
| ndarray.size |
数组元素的总个数,相当于 .shape 中 n*m 的值 |
| ndarray.dtype |
ndarray 对象的元素类型 |
| ndarray.itemsize |
ndarray 对象中每个元素的大小,以字节为单位 |
| ndarray.flags |
ndarray 对象的内存信息 |
| ndarray.real |
ndarray元素的实部 |
| ndarray.imag |
ndarray 元素的虚部 |
| ndarray.data |
包含实际数组元素的缓冲区,由于一般通过数组的索引获取元素,所以通常不需要使用这个属性。 |
4个必记参数:
ndim:维度 ;shape:形状(各维度的长度);size:总长度;dtype:元素类型
1、ndarray.ndim
ndarray.ndim用于返回数组的维数,等于秩。
In[ ]:
import matplotlib.pyplot as plt
cat = plt.imread('cat.jpg')
cat.ndim
3
2、ndarray.shape
ndarray.shape表示数组的维度,返回一个元组,这个元组的长度就是维度的数目,即 ndim 属性(秩)。比如,一个二维数组,其维度表示"行数"和"列数"。
ndarray.shape 也可以用于调整数组大小。
In[ ]:
image.shape
(10, 20, 3)
In[ ]:
a = np.array([[1,2,3],[4,5,6]])
print (a.shape)
(2, 3)
调整数组大小:
In[ ]:
a = np.array([[1,2,3],[4,5,6]])
a.shape = (3,2) #调整数组
print (a)
[[1 2]
[3 4]
[5 6]]
NumPy 也提供了 reshape 函数来调整数组大小。
In[ ]:
a = np.array([[1,2,3],[4,5,6]])
b = a.reshape(3,2)
print (b)
[[1 2]
[3 4]
[5 6]]
3、ndarray.size
数组元素的总个数,相当于 .shape 中 n*m 的值
In[ ]:
image.size
998640
4、ndarray.dtype
ndarray 对象的元素类型
In[ ]:
image.dtype
dtype('float64')
三、ndarray的基本操作
ndarray对象的内容可以通过索引或切片来访问和修改,与 Python 中 list 的切片操作一样。
ndarray 数组可以基于 0 - n 的下标进行索引,切片对象可以通过内置的 slice 函数,并设置 start, stop 及 step 参数进行,从原数组中切割出一个新数组。
1. 索引
一维与列表完全一致 多维时同理
In[ ]:
n1 = np.array([1,2,4,7,9])
n1[3]
7
可以根据索引修改数据
2. 切片
一维与列表完全一致 多维时同理
In[ ]:
a = np.arange(10)
b = a[2:7:2]
# 从索引 2 开始到索引 7 停止,间隔为 2
print(b)
[2 4 6]
冒号 : 的解释:如果只放置一个参数,如 [2],将返回与该索引相对应的单个元素。如果为 [2:],表示从该索引开始以后的所有项都将被提取。如果使用了两个参数,如 [2:7],那么则提取两个索引(不包括停止索引)之间的项。
In[ ]:
a = np.arange(10)
print(a[2:])
[2 3 4 5 6 7 8 9]
In[ ]:
a = np.arange(10)
# [0 1 2 3 4 5 6 7 8 9]
print(a[2:5])
[2 3 4]
多维数组同样适用上述索引提取方法。
切片还可以包括省略号 …,来使选择元组的长度与数组的维度相同。 如果在行位置使用省略号,它将返回包含行中元素的 ndarray。
In[ ]:
a = np.array([[1,2,3],[3,4,5],[4,5,6]])
print (a[...,1]) # 第2列元素
print (a[1,...]) # 第2行元素
print (a[...,1:]) # 第2列及剩下的所有元素
[2 4 5]
[3 4 5]
[[2 3]
[4 5]
[5 6]]
将数据反转,例如[1,2,3]---->[3,2,1]
In[ ]:
n = np.random.randint(0,100,size = 10)
n
array([21, 1, 4, 80, 28, 62, 69, 92, 76, 42])
In[ ]:
n[::-1]
array([42, 76, 92, 69, 62, 28, 80, 4, 1, 21])
In[ ]:
n[::-2]
array([42, 92, 62, 80, 1])
两个::进行切片
3. 变形
使用reshape函数,注意参数是一个tuple!
In[ ]:
import matplotlib.pyplot as plt
cat = plt.imread('cat.jpg')
plt.imshow(cat)
plt.show()
In[ ]:
cat.shape
(456, 730, 3)
In[ ]:
s1 = cat.size
n = np.random.randint(0,255,size = s1)
image2 = n.reshape((456,730,3))
plt.imshow(image2)
plt.show()
4. 级联
np.concatenate() 级联需要注意的点:
1. 级联的参数是列表:一定要加中括号或小括号
2. 维度必须相同
3. 形状相符
4. 【重点】级联的方向默认是shape这个tuple的第一个值所代表的维度方向
5. 可通过axis参数改变级联的方向
In[ ]:
n1 = np.random.randint(0,100,size = (4,2))
n2 = np.random.randint(-100,0,size = (4,6))
display(n1,n2)
array([[80, 65],
[ 8, 10],
[53, 10],
[55, 40]])
array([[-45, -55, -9, -3, -7, -49],
[-58, -83, -41, -30, -11, -68],
[-81, -3, -52, -5, -36, -44],
[-10, -30, -90, -63, -4, -1]])
对上面数组进行拼接
In[ ]:
newn = np.concatenate((n1,n2),axis = 1)
newn
array([[ 80, 65, -45, -55, -9, -3, -7, -49],
[ 8, 10, -58, -83, -41, -30, -11, -68],
[ 53, 10, -81, -3, -52, -5, -36, -44],
[ 55, 40, -10, -30, -90, -63, -4, -1]])
In[ ]:
newn.shape #由于axis = 1,新数组对列进行了拼接,即:6+2=8
(4, 8)
对于多维数组,比如之前的图片cat和image2
In[ ]:
#cat image2
image3 = np.concatenate((cat,image2),axis = 0)
image3.shape
(912, 730, 3)
np.hstack与np.vstack
水平级联与垂直级联,处理自己,进行维度的变更
In[ ]:
n = np.random.randint(0,100,size = (4,5))
n
array([[ 9, 66, 25, 35, 59],
[10, 29, 56, 24, 11],
[26, 9, 35, 51, 59],
[26, 34, 33, 78, 35]])
In[ ]:
#h = horizontal 水平
np.hstack(n)
array([ 9, 66, 25, 35, 59, 10, 29, 56, 24, 11, 26, 9, 35, 51, 59, 26, 34,
33, 78, 35])
In[ ]:
n = np.random.randint(0,10,size = 5)
n
array([7, 1, 8, 8, 7])
In[ ]:
np.vstack(n) #垂直方向
array([[7],
[1],
[8],
[8],
[7]])
对numpy.append()和numpy.concatenate()两个函数的运行时间进行比较
示例:
>>> from time import clock as now
>>> a=np.arange(9999)
>>> b=np.arange(9999)
>>> time1=now()
>>> c=np.append(a,b)
>>> time2=now()
>>> print time2-time1
28.2316728446
>>> a=np.arange(9999)
>>> b=np.arange(9999)
>>> time1=now()
>>> c=np.concatenate((a,b),axis=0)
>>> time2=now()
>>> print time2-time1
20.3934997107
可知,concatenate()效率更高,适合大规模的数据拼接
5. 切分
与级联类似,三个函数完成切分工作:
np.split
np.vsplit
np.hsplit
split(ary, indices_or_sections, axis=0) : 把一个数组从左到右按顺序切分
参数:
ary:要切分的数组
indices_or_sections:如果是一个整数,就用该数平均切分,如果是一个数组,为沿轴切分的位置(左开右闭)
axis:沿着哪个维度进行切向,默认为0,横向切分。为1时,纵向切分
比如:
In[ ]:
x = np.arange(9.0)
x
array([0., 1., 2., 3., 4., 5., 6., 7., 8.])
切分为3个数组
In[ ]:
np.split(x, 3) #”3”为切分的数目,也就是,最终被切分成3个数组
[array([0., 1., 2.]), array([3., 4., 5.]), array([6., 7., 8.])]
按照指定元素位置切分:
In[ ]:
np.split(x, [3, 5, 6, 10]) #使用中括号,按照元素切分
[array([0., 1., 2.]),
array([3., 4.]),
array([5.]),
array([6., 7., 8.]),
array([], dtype=float64)]
图片也是由数据组合出来的,因此,也可以进行切分:
In[ ]:
cat.shape
(456, 730, 3)
尝试切分
In[ ]:
s_result = np.split(cat,2,axis = 1)
s_result[0].shape #列切分,730的一半,365
(456, 365, 3)
In[ ]:
len(s_result)
2
In[ ]:
plt.imshow(s_result[0])
plt.show()
先生成一个随机的多维数组
In[ ]:
n = np.random.randint(0,100,size = (4,6))
n
array([[97, 14, 86, 68, 88, 57],
[51, 75, 64, 77, 7, 21],
[99, 68, 72, 51, 74, 61],
[26, 5, 2, 64, 18, 35]])
# 垂直方向分割 vsplit
In[ ]:
np.vsplit(n,(1,2)) #按照行从进行切分,1+1,2+1(也就是第1组与第2组之间、第2组与第3组之间)
[array([[97, 14, 86, 68, 88, 57]]),
array([[51, 75, 64, 77, 7, 21]]),
array([[99, 68, 72, 51, 74, 61],
[26, 5, 2, 64, 18, 35]])]
# 水平方向分割 hsplit
In[ ]:
np.hsplit(n,(2,4)) #按照列进行切分
[array([[97, 14],
[51, 75],
[99, 68],
[26, 5]]),
array([[86, 68],
[64, 77],
[72, 51],
[ 2, 64]]),
array([[88, 57],
[ 7, 21],
[74, 61],
[18, 35]])]
6. 副本
所有赋值运算不会为ndarray的任何元素创建副本。对赋值后的对象的操作也对原来的对象生效。
In[ ]:
n = np.array([1,2,3])
n[2] = 10
n
array([ 1, 2, 10])
可使用copy()函数创建副本
In[ ]:
n2 = n.copy()
n2[0] = 1024
n2
array([1024, 2, 10])
再看看n
In[ ]:
n
array([ 1, 2, 10])
四、ndarray的聚合操作
1. 求和np.sum
numpy的sum函数可接受的参数是:
sum(a, axis=None, dtype=None, out=None, keepdims=np._NoValue)
参数:
a是要进行加法运算的向量/数组/矩阵
axis的值有三种情况:1.None,2.整数, 3.整数元组。
(在默认/缺省的情况下,axis取None)
如果axis取None,即将数组/矩阵中的元素全部加起来,得到一个和。
In[ ]:
np.sum([0.5, 1.5])
2.0
In[ ]:
np.sum([0.5, 0.7, 0.2, 1.5], dtype=np.int32) #需要先转换为整数,1.5转换为1,其他是转换为0
1
In[ ]:
np.sum([[0, 1], [0, 5]])
6
如果axis为整数,axis的取值不可大于数组/矩阵的维度,且axis的不同取值会产生不同的结果。
先以2×2的二维矩阵为例:
In[ ]:
np.sum([[0, 1], [0, 5]], axis=0)
array([0, 6])
In[ ]:
np.sum([[0, 1], [0, 5]], axis=1)
array([1, 5])
2. 最大最小值:np.max/ np.min
min()
对于类型为array的数组,可以直接调用最小值的方法函数min(),和最大值方法函数max()。以下仅以min()为例说明,该函数具体用法与numpy.amin()类似。1
一个简单的应用实例为:
In[ ]:
from numpy import *
arrayTest = array([1,2,3,4,5])
arrayTest.min()
1
对于多维数组,可以对不同维度方向上的数据进行比较。数组维度为ndim,则min函数的变量即数组的方向,具体取值为小于ndim的非负整数,输出一个ndim-1维度的数组。
以二维矩阵为例,测试min(0):
In[ ]:
arrayTest = array([[1,6,3],[4,2,5]])
arrayTest.min(0)arrayTest = array([[1,6,3],[4,2,5]])
arrayTest.min(0) #min(0),(二位矩阵)数据取每一列的最小值
array([1, 2, 3])
In[ ]:
arrayTest = array([[1,6,3],[8,11,7],[4,2,5]])
arrayTest.min(1) #min(1),(二位矩阵)数据取每一行的最小值
array([1, 7, 2])
总结:
1)如果直接用min(),那么返回的是整个矩阵中元素的最小值
2)如果用min(0)或者min(axis=0)),那么返回的是所有列中每一列的最小值,返回一个1*n的数组
3)如果用min(1)或者min(axis=1)),那么返回的是所有行中每一行的最小值,返回一个1*n的数组
对于max()函数,也是一样的!
3. 其他聚合操作
Function Name NaN-safe Version Description
函数名 NaN-safe版本 说明
np.sum np.nansum Compute sum of elements(计算元素之和)
np.prod np.nanprod Compute product of elements(计算元素的乘积)
np.mean np.nanmean Compute mean of elements(计算元素平均值)
np.std np.nanstd Compute standard deviation(计算标准差)
np.var np.nanvar Compute variance(计算方差)
np.min np.nanmin Find minimum value(求最小值)
np.max np.nanmax Find maximum value(求最大值)
np.argmin np.nanargmin Find index of minimum value(求最小值索引)
np.argmax np.nanargmax Find index of maximum value(求最大值索引)
np.median np.nanmedian Compute median of elements(计算元素的中值)
np.percentile np.nanpercentile Compute rank-based statistics of elements(计算基于秩的元素统计)
np.any N/A Evaluate whether any elements are true(评估是否有任何元素是真的)
np.all N/A Evaluate whether all elements are true(评估所有元素是否是真的)
np.power 幂运算
五、ndarray的矩阵操作
1. 基本矩阵操作
1) 算术运算符:
- 加减乘除
In[ ]:
import numpy as np
n = np.random.randint(0,10,size = (4,5))
n
array([[2, 9, 1, 1, 2],
[2, 4, 5, 0, 2],
[6, 5, 8, 5, 5],
[8, 2, 8, 4, 1]])
In[ ]:
n + 10 #加10
array([[12, 19, 11, 11, 12],
[12, 14, 15, 10, 12],
[16, 15, 18, 15, 15],
[18, 12, 18, 14, 11]])
In[ ]:
n - 10 #减10
array([[ -8, -1, -9, -9, -8],
[ -8, -6, -5, -10, -8],
[ -4, -5, -2, -5, -5],
[ -2, -8, -2, -6, -9]])
In[ ]:
n * 6 #乘以6
array([[12, 54, 6, 6, 12],
[12, 24, 30, 0, 12],
[36, 30, 48, 30, 30],
[48, 12, 48, 24, 6]])
In[ ]:
n / 2 #除以2
array([[1. , 4.5, 0.5, 0.5, 1. ],
[1. , 2. , 2.5, 0. , 1. ],
[3. , 2.5, 4. , 2.5, 2.5],
[4. , 1. , 4. , 2. , 0.5]])
In[ ]:
#如果需要有值的变化,重新赋值给新的变量
n2 = n / 3
n2
array([[0.66666667, 3. , 0.33333333, 0.33333333, 0.66666667],
[0.66666667, 1.33333333, 1.66666667, 0. , 0.66666667],
[2. , 1.66666667, 2.66666667, 1.66666667, 1.66666667],
[2.66666667, 0.66666667, 2.66666667, 1.33333333, 0.33333333]])
In[ ]:
#也可以通过数学运算符,比如加运算函数add()
np.add(n,3)
array([[ 5, 12, 4, 4, 5],
[ 5, 7, 8, 3, 5],
[ 9, 8, 11, 8, 8],
[11, 5, 11, 7, 4]])
- 矩阵积np.dot()
In[ ]:
#数组n1乘以n2,也就是矩阵的乘法
np.dot(n1,n2)
#[[ 7*3+6*7+1*8, 7*1+6*8+1*6],[5*3+2*7+9*8, 5*1+2*8+9*6]]
array([[ 71, 61],
[101, 75]])
2. 广播机制
【重要】ndarray广播机制的两条规则
- 规则一:为缺失的维度补1
- 规则二:假定缺失元素用已有值填充
例1: m = np.ones((2, 3)) a = np.arange(3) 求M+a
In[ ]:
m = np.ones((2, 3))
a = np.arange(3)
print(m,a)
display(m,a)
[[1. 1. 1.]
[1. 1. 1.]] [0 1 2]
array([[1., 1., 1.],
[1., 1., 1.]])
array([0, 1, 2])
我们对m加a,看看会怎样?
In[ ]:
#numpy广播,机制,维度不对应,自动补全
m + a
array([[1., 2., 3.],
[1., 2., 3.]])
广播的规则:
- 让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐。
- 输出数组的形状是输入数组形状的各个维度上的最大值。
- 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错。
- 当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
简单理解:对两个数组,分别比较他们的每一个维度(若其中一个数组没有当前维度则忽略),满足:
- 数组拥有相同形状。
- 当前维度的值相等。
- 当前维度的值有一个是 1。
若条件不满足,抛出 "ValueError: frames are not aligned" 异常。
比如:
In[ ]:
a = np.array([[ 0, 0, 0], [10,10,10], [20,20,20], [30,30,30]])
b = np.array([1,2,3])
print(a + b)
[[ 1 2 3]
[11 12 13]
[21 22 23]
[31 32 33]]
下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。
4x3 的二维数组与长为 3 的一维数组相加,等效于把数组 b 在二维上重复 4 次再运算:
In[ ]:
a = np.array([[ 0, 0, 0], [10,10,10], [20,20,20], [30,30,30]])
b = np.array([1,2,3])
bb = np.tile(b, (4, 1)) # 重复 b 的各个维度
print(a + bb)
[[ 1 2 3]
[11 12 13]
[21 22 23]
[31 32 33]]
例2: a = np.arange(3).reshape((3, 1)) b = np.arange(3) 求a+b
习题 a = np.ones((4, 1)) b = np.arange(4) 求a+b
In[ ]:
a = np.arange(3).reshape((3, 1))
b = np.arange(3)
display(a,b)
print(a+b)
array([[0],
[1],
[2]])
array([0, 1, 2])
[[0 1 2]
[1 2 3]
[2 3 4]]
In[ ]:
a = np.ones((4, 1))
b = np.arange(4)
display(a,b)
print(a+b)
array([[1.],
[1.],
[1.],
[1.]])
array([0, 1, 2, 3])
[[1. 2. 3. 4.]
[1. 2. 3. 4.]
[1. 2. 3. 4.]
[1. 2. 3. 4.]]
六、ndarray的排序
小测验: 使用以上所学numpy的知识,对一个ndarray对象进行选择排序。
def Sortn(x):
代码越短越好
In[ ]:
n1 = np.array([2,5,1,7,4])
display(n1,n1.size)
array([2, 5, 1, 7, 4])
5
In[ ]:
def sortn(nd):
for i in range(nd.size):
for j in range(i,nd.size):
if nd[i] > nd[j]:
nd[i],nd[j] = nd[j],nd[i]
return nd
sortn(n1)
array([1, 2, 4, 5, 7])
如何增加运行效率,需要考虑!
In[ ]:
#之前已经对n1排序,重新定义
n1 = np.array([2,5,1,7,4])
#降低运算的空间复杂度和时间复杂度
def sortnd(nd):
for i in range(nd.size):
#由于使用切片,索引是不对应的
min_index = np.argmin(nd[i:]) + i
print(min_index)
sortnd(n1)
2
2
2
4
4
上面只是确定“min_index”
In[ ]:
#之前已经对n1排序,重新定义
n1 = np.array([2,5,1,7,4])
#降低运算的空间复杂度和时间复杂度
def sortnd(nd):
for i in range(nd.size):
#由于使用切片,索引是不对应的
min_index = np.argmin(nd[i:]) + i
# print(min_index)
nd[i],nd[min_index] = nd[min_index],nd[i]
return nd
sortnd(n1)
array([1, 2, 4, 5, 7])
1. 快速排序
np.sort()与ndarray.sort()都可以,但有区别:
np.sort()不改变输入
ndarray.sort()本地处理,不占用空间,但改变输入
In[ ]:
n1 = np.random.randint(0,150,size = 10)
n2 = np.sort(n1)
print("最初的n1:")
display(n1)
print("\n")
print("使用np.sort(n1)方法之后,n1:")
display(n1)
print("n2:")
display(n2)
print("使用n1.sort()方法之后,注意n1的变化!")
n3 = n1.sort() #不可以将原列表排序后,直接拷贝给新列表
print("n1:")
display(n1)
print("n3:")
display(n3)
最初的n1:
array([ 4, 86, 90, 79, 88, 118, 22, 139, 119, 10])
使用np.sort(n1)方法之后,n1:
array([ 4, 86, 90, 79, 88, 118, 22, 139, 119, 10])
n2:
array([ 4, 10, 22, 79, 86, 88, 90, 118, 119, 139])
使用n1.sort()方法之后,注意n1的变化!
n1:
array([ 4, 10, 22, 79, 86, 88, 90, 118, 119, 139])
n3:
None
不可以将原列表排序后,直接拷贝给新列表;但是可以在排序后,再赋值给新列表,分两步完成:
In[ ]:
ls=[1,2,3,4,1,4,4]
new_ls=[]
ls.sort(reverse=True)
new_ls=ls
print(new_ls)
[4, 4, 4, 3, 2, 1, 1]
2. 部分排序
np.partition(a,k)
有的时候我们不是对全部数据感兴趣,我们可能只对最小或最大的一部分感兴趣。
当k为正时,我们想要得到最小的k个数
当k为负时,我们想要得到最大的k个数
In[ ]:
n1 = np.random.randint(0,150,size = 10)
print("最初的n1:")
display(n1)
print("选出最小的5个数...")
n2 = np.partition(n1,-5)
print("不进行筛选的:")
print(n2)
print("筛选的5个数:")
print(n2[:5])
最初的n1:
array([ 7, 56, 29, 76, 28, 148, 78, 31, 146, 80])
选出最小的5个数...
不进行筛选的:
[ 7 28 29 31 56 76 78 80 146 148]
筛选的5个数:
[ 7 28 29 31 56]
仅供参考学习,严禁转载!