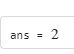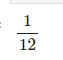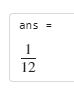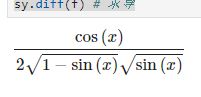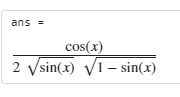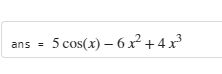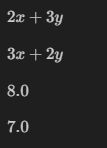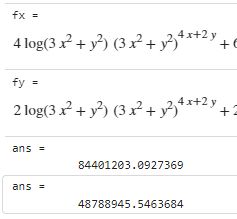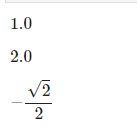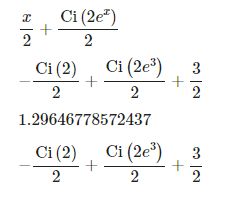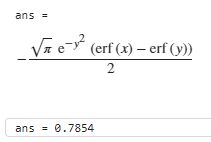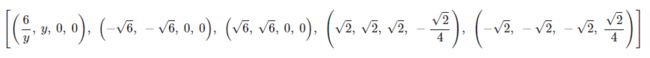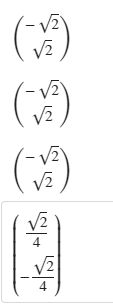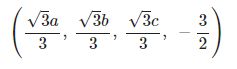数学与计算机（1）- 高等数学

(原文：https://blog.iyatt.com/?p=12906)

1 工具

1.1 Python

基础工具

• Python 3.11.2

数学模块

• SymPy 1.12
• SciPy 1.11.4
• NumPy 1.26.3

Scientific Python（SciPy）是一个基于 NumPy 的数值计算库，而 Symbolic Python（SymPy） 是一个符号计算库。

交互工具

• Jupyter Notebook 7.0.6

JN 具有笔记本功能，可以使用 Markdown 语法，支持 LaTex 公式，同时可以运行 Python 代码，记录运行结果，支持对式子以及分数的显示，而不是线性显示。
可以运行 Jupyter Notebook，然后网页访问，或者使用 VScode 也可以打开 .ipynb 文件。

数据可视化

• Matplotlib 3.8.2

1.2 MATLAB

MATLAB 2023b

2 极限

2.1 例 1

求 $$\lim_{x\to\infty}\frac{\sin x}{x}$$

SymPy

import sympy as sy

x = sy.Symbol('x') # 定义符号，用 Python 变量 x 表示符号 x
f = sy.sin(x) / x # 表达式
sy.limit(f, x, sy.oo) # 计算极限

MATLAB

syms x;

f = sin(x) / x;
limit(f, x, inf)

2.2 例 2

求 $$\lim_{x\to1}\frac{x^2-1}{x-1}$$

SymPy

import sympy as sy

x = sy.Symbol('x')
f = (x**2 - 1) / (x - 1)
sy.limit(f, x, 1)

MATLAB

syms x;

f = (x^2 - 1) / (x - 1);
limit(f, x, 1)

2.2 例 3

求 $$\lim_{x\to0}\frac{\sin x}{3x+x^3}$$

SymPy

import sympy as sy

x = sy.Symbol('x')
f = sy.sin(x) / (3 * x + x**3)
sy.limit(f, x, 0)

MATLAB

syms x;

f = sin(x) / (3 * x + x^3);
limit(f, x, 0)

2.4 例 4 无穷项

求$$\lim_{n\to\infty}\frac{1}{n^2}+\frac{2}{n^2}+\cdots+\frac{n}{n^2}$$

SymPy

import sympy as sy

n, t = sy.symbols('n t')
f = sy.summation(t / n**2, (t, 1, n))
print("表达式为：")
display(f)
print("计算极限结果为：")
sy.limit(f, n, sy.oo)

MATLAB

syms n t;

f = symsum(t / n^2, t, 1, n)
limit(f, n, inf)

2.5 例 5

求$$\lim_{x\to1}\sin(\ln x))$$

SymPy

import sympy as sy

x = sy.symbols('x')
f = sy.sin(sy.ln(x))
sy.limit(f, x, 1)

MATLAB

syms x;

f = sin(log(x))
limit(f, x, 1)

2.6 例6

求$$\lim_{x\to8}\frac{\sqrt[3]{x}-2}{x-8}$$

SymPy

import sympy as sy

x = sy.symbols('x')
f = (sy.root(x, 3) - 2) / (x - 8)
sy.limit(f, x, 8)

MATLAB

syms x;

f = (x^(1/3) - 2) / (x - 8);
limit(f, x, 8)

3 导数

人工求导方法参考：https://blog.iyatt.com/?p=7986

3.1 例 1

对 $$y=\arcsin\sqrt{\sin x}$$ 求导

SymPy

import sympy as sy
from sympy.abc import x # 这个模块定义了常用符号变量，涵盖大小写字母

f = sy.asin(sy.sqrt(sy.sin(x)))
sy.diff(f) # 求导

MATLAB

syms x;

f = asin(sqrt(sin(x)));
diff(f)

3.2 例 2 计算导数值（含定义求导）

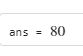
$$f(x)=x^5$$，计算f’(2)

SymPy

import sympy as sy

x = sy.symbols('x')
f = x**5
sy.diff(f).evalf(subs={x:2})

MATLAB

syms x;

f = x^5;
df = diff(f);
subs(df, x, 2)

基于定义

def f(x):
    return x**5

def derivative(x, h):
    return (f(x + h) - f(x)) / h

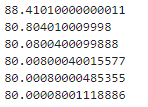
print(derivative(2, 1e-1))
print(derivative(2, 1e-2))
print(derivative(2, 1e-3))
print(derivative(2, 1e-4))
print(derivative(2, 1e-5))
print(derivative(2, 1e-6))

取的两个点越逼近，近似值越接近

3.3 例 3

对 $$y=x^4-2x^3+5\sin x+\ln3$$ 求导

SymPy

import sympy as sy

x = sy.symbols('x')
f = x**4 - 2 * x**3 + 5 * sy.sin(x) + sy.ln(3)
sy.diff(f)

MATLAB

syms x;

f = x^4 - 2 * x^3 + 5 * sin(x) +log(3);
diff(f)

4 偏导数

4.1 例 1

求 $$f(x,y)=x^2+3xy+y^2$$在点(1,2)处的偏导数

SymPy

import sympy as sy
from sympy.abc import x, y

f = x**2 + 3 * x * y + y**2

fx = sy.diff(f, x) # 求 x 偏导
display(fx)

fy = sy.diff(f, y) # 求 y 偏导
display(fy)

fxv = fx.evalf(subs={x:1, y:2}) # 求 x 偏导值
display(fxv)

fyv = fy.evalf(subs={x:1, y:2}) # 求 y 偏导值
display(fyv)

SciPy

from scipy.optimize import approx_fprime

def f(xy):
    x, y = xy
    return x**2 + 3 * x * y + y**2

approx_fprime([1,2], f, 1e-6)

MATLAB

syms x y;

f = x^2 + 3 * x * y + y^2;

fx = diff(f, x)
fy = diff(f, y)

subs(fx, [x, y], [1, 2])
subs(fy, [x, y], [1, 2])

4.2 例 2

已知$$z=(3x^2+y^2)^{4x+2y}$$，求在点(1,2)处的偏导数

SymPy

import sympy as sy

x, y = sy.symbols("x y")
f = (3 * x**2 + y**2)**(4 * x + 2 * y)

fx = sy.diff(f, x)
display(fx)

fy = sy.diff(f, y)
display(fy)

fxv = fx.evalf(subs={x:1, y:2})
display(fxv)

fyv = fy.evalf(subs={x:1, y:2})
display(fyv)

SciPy

from scipy.optimize import approx_fprime

def f(xy):
    x, y = xy
    return (3 * x**2 + y**2)**(4 * x + 2 * y)

approx_fprime([1, 2], f, 1e-100)

MATLAB

format longG % 不使用科学计数法显示，支持最多 15 位有效数字
syms x y;

f = (3 * x^2 + y^2)^(4 * x + 2 * y);

fx = diff(f, x)
fy = diff(f, y)

eval(subs(fx, [x, y], [1, 2]))
eval(subs(fy, [x, y], [1, 2]))

5 方向导数

5.1 例 1

求函数 $$z=xe^{2y}$$在点P(1,0)处沿从点P(1,0)到点Q(2,1)方向的方向导数

SymPy

计算角度

import sympy as sy

P = sy.Point(1, 0)
Q = sy.Point(2, -1)
PQ = sy.Line(P, Q).direction # 直线的向量
angle_rad_xol = sy.atan(PQ.y / PQ.x) # 从 x 轴转到 l 的角度
display(angle_rad_xol)

计算方向导数

from sympy.abc import x, y

f = x * sy.E**(2 * y)

fxv = sy.diff(f, x).evalf(subs={x:1, y:0})
display(fxv) # x 偏导值

fyv = sy.diff(f, y).evalf(subs={x:1, y:0})
display(fyv) # y 偏导值

flv = fxv * sy.cos(angle_rad_xol) + fyv * sy.sin(angle_rad_xol)
sy.nsimplify(flv) # 简化，不然这里可能显示成 -0.5\sqrt(2)

SciPy、NumPy
计算角度

import numpy as np

P = np.array([1, 0])
Q = np.array([2, -1])
angle_rad_xol = np.arctan2(Q[1] - P[1], Q[0] - P[0])
display(angle_rad_xol)

计算方向导数

from scipy.optimize import approx_fprime

def f(xy):
    x, y = xy
    return x * np.exp(2 * y)

grad = approx_fprime([1, 0], f, 1e-6) # 计算梯度
np.dot(grad, np.array([np.cos(angle_rad_xol), np.sin(angle_rad_xol)]))

MATLAB

syms x, y;

P = [1, 0];
Q = [2, -1];

angle_rad_xol = atan((Q(2) - P(2)) / (Q(1) - P(1)));

f = x * exp(2 * y);

fx = diff(f, x);
fy = diff(f, y);

fxv = subs(fx, [x, y], [1, 0]);
fyv = subs(fy, [x, y], [1, 0]);

flv = fxv * cos(angle_rad_xol) + fyv * sin(angle_rad_xol);
eval(flv)

6 梯度

梯度是一个向量，数值上由偏导数组成。在一个曲面上的某点处，梯度方向的变化率最快。

6.1 例 1 梯度下降法求最小值 - 绘图

$$f(x,y)=x-y+2x^2+2xy+y^2$$，初值为(2,2)，求最小值点

求解实现

%matplotlib widget
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# 原函数
def f(x, y):
    return x - y + 2 * x**2 + 2 * x * y + y**2

# 关于 x 的偏导数
def fx(x, y):
    return 1 + 4 * x + 2 * y

# 关于 y 的偏导数
def fy(x, y):
    return -1 + 2 * x + 2 * y

# x = np.linspace(-2, 2, 100)
# y = np.linspace(-2, 2, 100)
# X, Y = np.meshgrid(x, y)
X, Y = np.mgrid[-2:2:100j, -2:2:100j] # 也可以使用上面的写法生成网格坐标矩阵
Z = f(X, Y)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, cmap='rainbow') # 绘制原函数

# 坐标轴标签
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')


# 梯度下降
###########

# 步长
step = 0.0008

# 起始点
new_x = 2
new_y = 2

x = new_x
y = new_y

xs = [x]
ys = [y]
zs = [f(x, y)]

Over = False

while Over == False:
    new_x -= step * fx(x, y)
    new_y -= step * fy(x, y)

    if f(x, y) - f(new_x, new_y) < 7e-9:
        Over = True

    x = new_x
    y = new_y

    xs.append(x)
    ys.append(y)
    zs.append(f(x, y))

ax.plot(xs, ys, zs, color='k') # 绘制路径
print('({},{},{})'.format(xs[-1], ys[-1], zs[-1])) # 最小值点

图中曲面里的那条黑线就是从(2,2)最快走到曲面最低点的路径
求原函数一阶偏导为 0 的点可以得到(x,y)~(-1,1.5)，即在这个位置可能是一个极值，和绘图找出的点匹配，说明这个点就是要找的点，只是因为绘图所取步长的影响，绘图找出的点是一个近似值。如果步长无限的小，那么最终就是一个无限逼近的最小值点。

7 积分

人工计算参考：https://blog.iyatt.com/?p=11227

7.1 例 1

计算$$\int_0^3\cos^2(e^x)dx$$

SymPy

import sympy as sy

x = sy.symbols('x')
f = sy.cos(sy.E**x)**2

indefinite_integral = sy.integrate(f, x) # 不定积分
display(indefinite_integral)

definite_integral = indefinite_integral.subs(x, 3) - indefinite_integral.subs(x, 0) # 定积分（牛顿-莱布尼茨公式）
display(definite_integral)
display(sy.N(definite_integral)) # Ci 是余弦积分函数，这里可以转为数值的

display(
    sy.integrate(f, (x, 0, 3)) # 直接计算定积分
)

MATLAB

syms x;

f = cos(exp(x))^2;
indefinite_integral = int(f, x) % 计算不定积分

definite_integral1 = subs(indefinite_integral, x, 3) - subs(indefinite_integral, x, 0) % 定积分（牛顿-莱布尼茨公式）

definite_integral2 = int(f, x, 0, 3) % 含表达式的结果
eval(definite_integral2) % 转为数值的结果

SciPy

from scipy.integrate import quad
import numpy as np

f = lambda x: np.cos(np.exp(x))**2
display(quad(f, 0, 3)) # 显示结果为积分值和误差

基于定义求近似值

import numpy as np

a = 0 # 上限
b = 3 # 下限

def f(x):
    return np.cos(np.exp(x))**2

def trape(n):
    sum = 0
    x1 = a
    step = (b - a) / n # 步长
    for i in range(n):
        x2 = a + i * step
        sum += (f(x1) + f(x2)) * step / 2 # 累加小梯形
        x1 = x2
    return sum

print(trape(10))
print(trape(100))
print(trape(1000))
print(trape(10000))
print(trape(100000))

步长越小，小梯形越小，计算结果就越接近

7.2 例 2

SymPy

import sympy as sy

x, y = sy.symbols('x y')
f = sy.E**(-x**2 - y**2)
display(sy.integrate(f, x, y)) # 不定积分
definite_integral = sy.integrate(f, (x, 0, 10), (y, 0, 10)) # 定积分
display(definite_integral)
display(sy.N(definite_integral)) # 数值近似值

SciPy

import numpy as np
from scipy.integrate import dblquad

def f(x, y):
    return np.exp(-x**2 - y**2)

dblquad(f, 0, 10, lambda y: 0, lambda y: 10) # y 的上下限建议定义函数或者使用 lambda 表达式

MATLAB

syms x y;

f = exp(-x^2 - y^2);
int(f, x, y) % 不定积分

f = @(x, y) exp(-x.^2 - y.^2);
integral2(f, 0, 10, 0, 10) % 定积分

7.3 例 3

$$\int_1^2(x^2+\frac{1}{x^4})dx$$

SymPy

import sympy as sy

x = sy.symbols('x')
f = x**2 + 1 / x**4
di = sy.integrate(f, (x, 1, 2))
display(di)
sy.N(di)

SciPy

from scipy.integrate import quad

def f(x):
    return x**2 + 1 / x**4

quad(f, 1, 2)

MATLAB

syms x;

f = x^2 + 1 / x^4;
di = int(f, x, 1, 2);
disp(di)
disp(vpa(di)) % 转小数

7.4 例 4

$$\int_{-1}^0\frac{3x^4+3x^2+1}{x^1+1}dx$$

SymPy

import sympy as sy

x = sy.symbols('x')
f = (3 * x**4 + 3 * x**2 + 1) / (x**2 + 1)
definite_integral = sy.integrate(f, (x, -1, 0))

display(definite_integral)
display(sy.N(definite_integral))

SciPy

from scipy.integrate import quad

def f(x):
    return (3 * x**4 + 3 * x**2 + 1) / (x**2 + 1)

quad(f, -1, 0)

MATLAB

syms x;

f = (3 * x^4 + 3 * x^2 + 1) / (x^2 + 1);
definite_integral = int(f, x, -1, 0)
vpa(definite_integral)

7.5 例 5 基于积分定义（黎曼和）计算

$$\lim_{n\to\infty}\frac{1^p+2^p+\cdots+n^p}{n^{p+1}}，(p\gt0)$$

这个我用 SymPy 和 MATLAB 把式子表示出来了，但是都无法计算，SymPy 报错，MATLAB 把表达式作为结果显示出来，都无法计算。

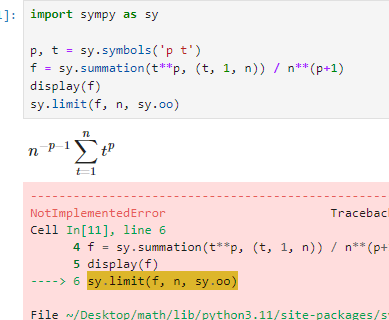
所以得回到积分定义来做。
假如要求一个函数从x=0到x=E范围内和x轴围起来的部分的面积，那么可以看做无限个小长方形之和（黎曼和）。分为n个小长方形，每个小长方形的宽就是$$\frac En$$，高就是$$f(\frac {iE}{n})$$，i对应从0开始的第i个长方形。

\begin{aligned}
\int_0^Ef(x)dx&=\lim_{n\to\infty}[f(\frac{E}{n})\cdot\frac{E}{n}+f(\frac{2E}{n})\cdot\frac{E}{n}+\cdots+f(\frac{nE}{n})\frac{E}{n}] \\
&=\lim_{n\to\infty}\frac{E}{n}\cdot\sum_{i=1}^n\frac{iE}{n}
\end{aligned}

若范围不是0到E，而是指定从S开始到E，那么有

\begin{aligned}
\int_S^Ef(x)dx&=\lim_{n\to\infty}[f(S+\frac{E-S}{n})\cdot\frac{E-S}{n}+f(\frac{S+2(E-S)}{n})\cdot\frac{E-S}{n}+\cdots+f(S+\frac{n(E-S)}{n})\frac{E-S}{n}] \\
&=\lim_{n\to\infty}\frac{E-S}{n}\cdot\sum_{i=1}^n[S+\frac{i(E-S)}{n}]
\end{aligned}

再回到上面的题目

\begin{aligned}
原式&=\lim_{n\to+\infty}\sum_{i=1}^n\frac{i^p}{n^{p+1}}\\
&=\lim_{n\to+\infty}\frac{1}{n}\sum_{i=1}^n(\frac{i}{n})^p\\
&=\int_0^1x^pdx\\
&=\frac{1}{p+1}x^{p+1}|_0^1\\
&=\frac{1}{p+1}
\end{aligned}

8 泰勒公式

泰勒定理参考：https://blog.iyatt.com/?p=10375

8.1 例 1 e^x 麦克劳林展开

\begin{aligned}
&
\begin{aligned}
e^x&=f(0)+\frac{f'(0)}{1!}(x-0)+\frac{f''(0)}{2!}(x-0)^2+\cdots+\frac{f^{(n)}}{n!}(x-0)^n \\
&=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}\\
\end{aligned}
\\
&|R_n(x)|=|\frac{e^{\theta x}}{(n+1)!}|\lt\frac{e^{|x|}}{(n+1)!}，0\lt\theta\lt x
\end{aligned}

若x=1,则有

e=1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{n!}，|R_n|\lt\frac{e}{(n+1)!}\lt\frac{3}{(n+1)!}

n=10时，$$e\approx2.718281801$$，误差不超过$$10^{-7}$$

Python 模拟计算过程

def f(n):
    sum = 1
    if n == 1:
        return sum
    else:
        for i in range(1, n):
            factorial = 1
            factorial_end = i + 1
            for j in range(1, factorial_end): # 阶乘
                factorial *= j
            sum += (1.0 / factorial)
    return sum

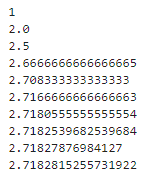
print(f(1))
print(f(2))
print(f(3))
print(f(4))
print(f(5))
print(f(6))
print(f(7))
print(f(8))
print(f(9))
print(f(10))

SymPy

import sympy as sy

x = sy.symbols('x')
f = sy.E**x
display(sy.series(f)) # 默认麦克劳林展开
taylor = sy.series(f, x, 0, 10) # 指定在 0 处展开即麦克劳林，并指定展开 10 阶
display(taylor)
display(taylor.removeO().evalf(subs={x:1})) # 先移除高阶无穷小再代值计算

MATLAB

syms x;

f = exp(x);
taylor(f) % 默认麦克劳林展开
ft = taylor(f, x, 'Order', 10) % 展开 10 阶
vpa(subs(ft, x, 1)) % 代值计算

8.2 例 2 sin x 麦克劳林展开

\begin{array}{l}
f(x)=\sin x \\
f'(x)=\cos x \\
f''(x)=-\sin x \\
f^{(3)}(x)=-\cos x \\
f^{(4)}(x)=\sin x \\
\\
f(x)=0+x+0-\frac{1}{3!}x^3+0+\frac{1}{5}x^5+0-\frac{1}{7}x^7+\cdots+(-1)^{m-1}\frac{x^{2m-1}}{2m-1}+R_{2m}(x)\\
R_{2m}(x)=\frac{\sin[\theta x+(2m+1)\cdot\frac{\pi}{2}]}{(2m+1)!}x^{2m+1}=(-1)^m
\frac{\cos\theta x}{(2m+1)!}x^{2m+1}，0\lt\theta\lt1
\end{array}

9 拉格朗日乘子法

9.1 例 1

已知目标函数V(x,y,z)=xyz，在约束条件2xy+2xz+2yz=12下，求体积V的最大值。

令G(x)=2xy+2xz+2yz-12
则有

\left \{
\begin{array}{l}
\frac{\partial V}{\partial x}=-\lambda\frac{\partial G}{\partial x}\\ \\
\frac{\partial V}{\partial y}=-\lambda\frac{\partial G}{\partial y}\\ \\
\frac{\partial V}{\partial z}=-\lambda\frac{\partial G}{\partial z}\\ \\
G(x)=0
\end{array}
\right .

\left \{
\begin{array}{l}
yz+\lambda(2y+2z)=0 \\
xz+\lambda(2x+2z)=0 \\
xy+\lambda(2x+2y)=0 \\
2xy+2xz+2yz-12 = 0
\end{array}
\right .

SymPy 解方程组

import sympy as sy

sy.init_printing(use_unicode=True) # 使用 Unicode 显示，保证这里的解能以手写格式显示

x, y, z, t = sy.symbols('x y z t')
f1 = sy.Eq(y * z + t * (2 * y + 2 * z), 0)
display(f1)
f2 = sy.Eq(x * z + t * (2 * x + 2 * z), 0)
display(f2)
f3 = sy.Eq(x * z + t * (2 * x + 2 * y), 0)
display(f3)
f4 = sy.Eq(2 * x * y + 2 * x * z + 2 * y * z, 12)
display(f4)

sy.solve((f1, f2, f3, f4), (x, y, z, t))

因为方程组存在线性相关，所以解不只一个。V(x)的二阶偏导恒为0，所以没法用二阶偏导确定最大值，还在这里方程简单，直接用求出的点代入试就行。
在$$(\sqrt2,\sqrt2,\sqrt2)$$处，$$\lambda=-\frac{\sqrt2}{4}$$时，V(x)有最大值$$2\sqrt2$$

MATLAB 求解上面的方程组

syms x y z t;

f1 = y * z + t * (2 * y + 2 * z) == 0;
f2 = x * z + t * (2 * x + 2 * z) == 0;
f3 = x * y + t * (2 * x + 2 * y) == 0;
f4 = 2 * x * y + 2 * x * z + 2 * y * z == 12;

sol = solve(f1, f2, f3, f4);
disp(sol.x)
disp(sol.y)
disp(sol.z)
disp(sol.t)

9.2 例 2

已知目标函数为$$u=x^3y^2z$$，约束条件x+y+z=12，求最大值

\left \{
\begin{array}{l}
3x^2y^2z+\lambda = 0 \\
2x^3yz+\lambda=0 \\
x^3y^2 + \lambda=0\\
x+y+z=12
\end{array}
\right .

SymPy 解方程组

import sympy as sy

x, y, z, t = sy.symbols('x y z t')
f1 = sy.Eq(3 * x**2 * y**2 * z + t, 0)
f2 = sy.Eq(2 * x**3 * y * z + t, 0)
f3 = sy.Eq(x**3 * y**2 + t, 0)
f4 = sy.Eq(x + y + z, 12)

sy.solve((f1, f2, f3, f4))

其中(6, 4, 2)，$$\lambda=-3456$$时，$$u_{max}=6912$$

9.3 例 3

在第一象限内做椭球面$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$的切平面，使切平面与 3 个坐标轴面围城的四面体体积最小，求切点坐标。

设$$p(x_0,y_0,z_0)$$为椭球面上的一点（作为切点），令$$F(x,y,z)=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1$$
p点处的偏导数为

\begin{array}{l}
F_x'|_p=\frac{2x_0}{a^2} \\ \\
F_y'|_p=\frac{2y_0}{b^2} \\ \\
F_z'|_p=\frac{2z_0}{c^2}
\end{array}

过p点的切平面方程为

\begin{aligned}
\frac{2x_0}{a^2}(x-x_0)+\frac{2y_0}{b^2}(y-y_0)+\frac{2z_0}{c^2}(z-z_0)&=0 \\
\frac{x_0}{a^2}(x-x_0)+\frac{y_0}{b^2}(y-y_0)+\frac{z_0}{c^2}(z-z_0)&=0 \\
\frac{xx_0}{a^2}+\frac{yy_0}{b^2}+\frac{zz_0}{c^2}&=\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}+\frac{z_0^2}{c^2}\xlongequal{(x_0,y_0,z_0)在椭球面上}1 \\
即有\frac{xx_0}{a^2}+\frac{yy_0}{b^2}+\frac{zz_0}{c^2}&=0
\end{aligned}

可以得到切平面与 3 轴的截距$$x=\frac{a^2}{x_0}$$、$$y=\frac{b^2}{y_0}$$、$$z=\frac{c^2}{z_0}$$
切平面和 3 轴围成的面构成的四面体体积 $$V=\frac{1}{2}\cdot\frac{a^2}{x_0}\cdot\frac{b^2}{y_0}\cdot\frac{1}{3}\cdot\frac{c^2}{z_0}=\frac{a^2b^2c^2}{6x_0y_0z_0}$$

目标函数就是$$V=\frac{a^2b^2c^2}{6x_0b_0z_0}$$，约束条件为$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

求V最小时，实际就是求$$x_0y_0z_0$$最大时，那么可以当做求$$\ln(x_0y_0z_0)=\ln(x_0)+\ln(y_0)+\ln(z_0)$$最大时
构造函数：$$F(x,y,z,\lambda)=\ln x_0+\ln y_0+\ln z_0+\lambda(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1)$$
列方程组

\left \{
\begin{array}{l}
\frac{1}{x_0}+2\lambda\frac{x_0}{a^2}=0\\ \\
\frac{1}{y_0}+2\lambda\frac{y_0}{b^2}=0\\ \\
\frac{1}{z_0}+2\lambda\frac{z_0}{b^2}=0\\ \\
\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1
\end{array}
\right .

SymPy 求解

import sympy as sy

x0, y0, z0, a, b, c = sy.symbols('x0 y0 z0 a b c', positive=True) # 切点在第一象限必然为正
t = sy.symbols('t')

f1 = sy.Eq(1 / x0 + 2 * t * x0 / a**2, 0)
f2 = sy.Eq(1 / y0 + 2 * t * y0 / b**2, 0)
f3 = sy.Eq(1 / z0 + 2 * t * z0 / c**2, 0)
f4 = sy.Eq(x0**2 / a**2 + y0**2 / b**2 + z0**2 / c**2, 1)

for result in sy.solve((f1, f2, f3, f4), (x0, y0, z0, t)):
    display(result)

切点为$$(\frac{\sqrt3a}{3},\frac{\sqrt3b}{3},\frac{\sqrt3c}{3})$$时，$$V_{min}=\frac{\sqrt3}{2}abc$$