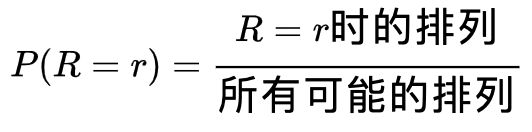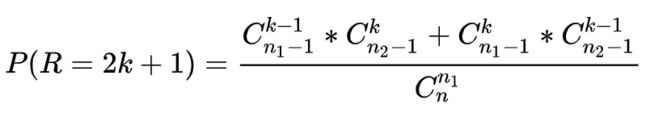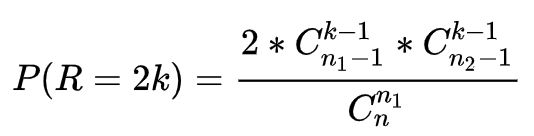游程检验和随机性检验

1 游程检验的含义

什么叫游程检验（Runs test）呢？

游程检验的定义：亦称“连贯检验”，是根据样本标志表现排列所形成的游程的多少进行判断的检验方法。

游程（Run）的定义：连续出现同一样本的区段，有几个区段就表明有几个游程，每个游程包含的样本个数为该游程的长度。

比如有如下三种排列：

• 男\男，女\女\女，男，女\女，男\男\男\男

• 男\男\男\男\男\男\男，女\女\女\女\女

• 男，女，男，女，男，女，男，女，男，女，男\男

角度1：上述三种排列对应的游程个数分别为5，2，11

角度2：直观上看出第1种排列为随机序列，第2、3种排列为非随机序列（有某种规律在）

因此，是否可以通过游程个数来检验样本的随机性（即样本随机性检验）？以及通过游程的个数来判断两种排列的一致性（即两总体分布一致性检验）？ 这就对应游程检验的两个典型应用！

2 应用1：两总体分布一致性检验

2.1 定义及解决的问题

定义：根据从两总体中抽样的结果，运用游程检验来判断两总体的分布是否具有一致性！

解决的问题：判断两总体分布是否具有一致性

2.2 原理

如果两总体分布一致，此时游程数较多，具体见下图：

如果两总体分布不一致，此时游程数较少，具体见下图：

因此接下来的问题就是，游程数的临界值应该设为多少才是分布一致？对应的置信度又是如何？这就是【游程检验】需要做的事情，游程检验本质上是一种非参数检验，即对总体没有很多假定的假设检验。

这种检验的步骤是三部曲：

• 提出假设
• 计算检验统计量
• 做出决策

遵循的原理是：“小概率原理”（小概率事件在一次具体实施中不会出现），即在原假设成立的情况下，某一事件发生概率很小，但如果它就发生了，那么就说明原假设有问题，需要推翻它。

2.2.1 Step1：提出假设

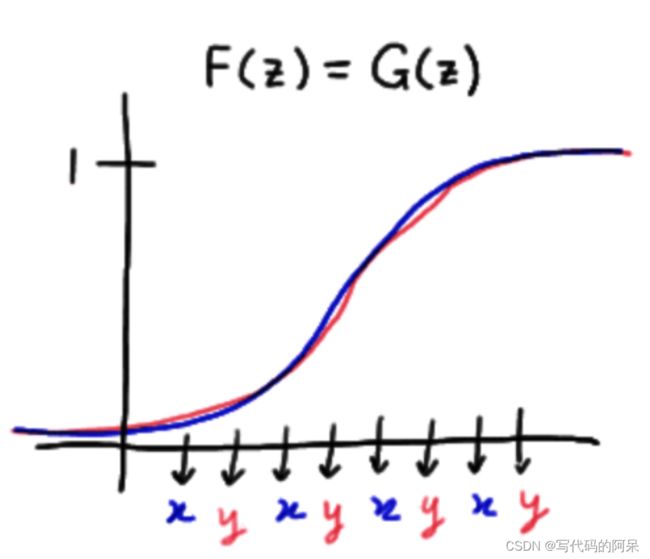
H0:F(z) = G(z) # 两总体分布一致

H1:F(z) ≠ G(z) # 两总体分布不一致

2.2.2 Step2：计算检验统计量

计算出游程数R=r的概率：（考虑到所有不同的排列）

2.2.3 Step3：决策

假如置信度为0.95（95%的置信水平），计算出P(R≤r)=0.05

• 这时候如果样本的游程个数小于等于r，则小概率事件发生了，在5%的显著性水平下可以拒绝原假设，认为两个分布不一致。
• 如果游程个数大于r，则不拒绝原假设，认为两个分布一致。

注：如果是在大样本情况下，由中心极限定理，总游程个数服从正态分布，此时有：

2.3 Python实现

举一个例子：判断x和y的总体分布是否相同：

x = [16.75, 19.25, 22, 20.5, 22.5, 15.5, 17.25, 20.75]
y = [24.75, 21.5, 19.75, 17.5, 22.75, 23.5, 13, 19]

进行升序排列后：

y xxx yy x y xx y xx yyy

即总共有9个游程，x有4个，y有5个~

经过计算，P(R≤6)=0.1002，即原假设成立情况下，总游程数小于等于6的概率为10%，而目前游程数为9个，所以没有发生小概率事件，也就不拒绝原假设了，认为两总体分布是一致的，置信度有90%。

from statsmodels.sandbox.stats.runs import runstest_2samp
runstest_2samp(x,y)

(0.25877458475338283, 0.7958091685190174)

第一个返回结果为检验统计量的值，第二个结果为P值，在显著性水平为5%时，不拒绝原假设~认为两总体分布一致。

3 应用2：样本随机性检验（单总体）

3.1 定义及解决的问题

通过游程检验来判断一个序列是否为随机的。

3.2 原理

如何判断呢？首先还是从直观的例子入手：

• 如果一个序列具有某种趋势，那么它的游程就会很少，例如：XXXXYYYYYY
• 如果一个序列具有某种周期性，那么它的游程就会很多，例如：XYXYXYXYXY

因此如果一个序列为随机那么游程不会很多，也不会很少~，即多于趋势序列的游程但少于周期序列的游程

3.2.1 Step1：提出假设

原假设：序列是随机的

备择假设：序列非随机

3.2.2 Step2：计算检验统计量

计算游程的个数，和上述2.2.2一致~

3.2.3 Step3:决策

拒绝域法：当游程个数大于某一个临界值或者小于某一个临界值 都是非随机的~

假如置信度为0.95（95%的置信水平），计算出P(R≤r1)+P(R≥r2)=0.05

• 这时候如果样本的游程个数小于等于r1或者大于等于r2，则小概率事件发生了，在5%的显著性水平下可以拒绝原假设，认为序列是非随机的。
• 如果游程个数在r1和r2之间，则不拒绝原假设，认为序列随机。

3.3 Python实现

举例：

x = [68.2, 71.6, 69.3, 71.6, 70.4, 65, 63.6, 64.7, 
     65.3, 64.2, 67.6, 68.6, 66.8, 68.9, 66.8, 70.1]

首先要计算这组数据的游程，所以需要先进行离散化的处理，可以有如下两种方法：

• 根据是否大于中位数分为两组
• 根据是否大于平均数分为两组

比如按照中位数来，大于等于中位数记为X，小于记为Y，那么：

XXXXX YYYYYY X Y X Y X

游程数为7个，计算得到 P(R≤4)+P(R≥14)=0.018

此时在1.8%的显著性水平下，不拒绝原假设(7在两个值之间)，即认为这个序列是一个随机序列。

from statsmodels.sandbox.stats.runs import runstest_1samp
runstest_1samp(x,cutoff='median')

(-0.7763237542601485, 0.4375578509038419)

不拒绝原假设，和上述结论一致~