算法---二分算法
详解二分查找算法
Although the basic idea of binary search is comparatively
straightforward, the details can be surprisingly tricky…
思路很简单,细节是魔鬼。
一:二分法算法分析
1、二分查找算法定义
二分查找又称折半查找,它是一种效率较高的查找方法。
二分查找要求:线性表是有序表,即表中结点按关键字有序,并且要用向量作为表的存储结构。
2、基本思想
(1)首先确定该区间的中点位置
(2)将待查的K值与R[mid]比较:若相等,则查找成功并返回此位置,否则须确定新的查找区间,继续二分查找
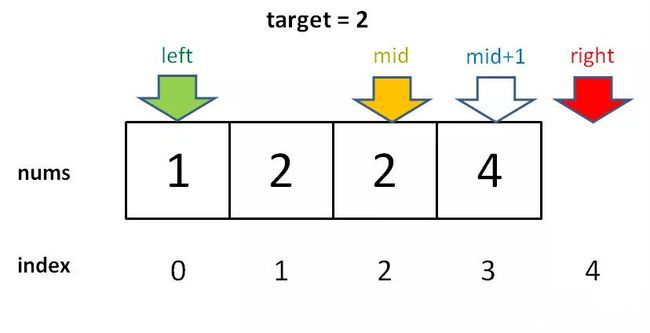
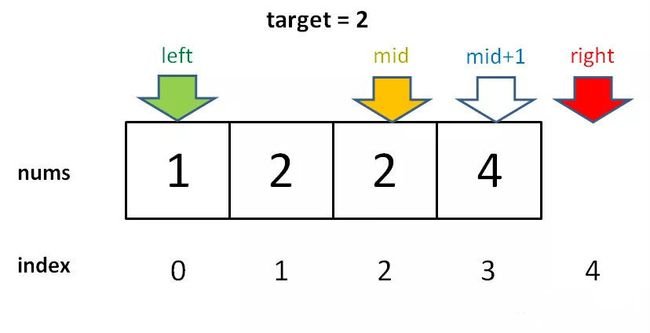
(3) ① 若R[mid].key>K,将查找区间变为**[left,mid-1]**
②若R[mid].key ③ 二分查找的优点 折半查找的时间复杂度为O(logn),远远好于顺序查找的O(n)。 ④ 二分查找的缺点 虽然二分查找的效率高,但是要将表按关键字排序。而排序本身是一种很费时的运算。既使采用高效率的排序方法也要花费O(nlgn)的时间。 寻找一个数、寻找左侧边界、寻找右侧边界。 细节: while循环中的不等号是否应该带等号,mid 是否应该加一等等。 分析二分查找的一个技巧是:不要出现 else,而是把所有情况用 else if 写清楚,这样可以清楚地展现所有细节 计算 mid 时需要技巧防止溢出,建议写成: mid = left + (right - left) / 2 搜索一个数,如果存在,返回其索引,否则返回 -1。 1. 为什么 while 循环的条件中是 <=,而不是 < ? 答:因为初始化 right 的赋值是 nums.length - 1,即最后一个元素的索引,而不是 nums.length。 这二者可能出现在不同功能的二分查找中,区别是:前者相当于两端都闭区间 [left, right],后者相当于左闭右开区间 [left, right),因为索引大小为 nums.length 是越界的。 我们这个算法中使用的是 [left, right] 两端都闭的区间。这个区间就是每次进行搜索的区间,我们不妨称为「搜索区间」(search space)。 什么时候应该停止搜索呢?当然,找到了目标值的时候可以终止: 但如果没找到,就需要 while 循环终止,然后返回 -1。那 while 循环什么时候应该终止?搜索区间为空的时候应该终止,意味着你没得找了,就等于没找到嘛。 while(left <= right)的终止条件是 left == right + 1,写成区间的形式就是 [right + 1, right],或者带个具体的数字进去 [3, 2],可见这时候搜索区间为空,因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的,直接返回 -1 即可。 while(left < right)的终止条件是 left == right,写成区间的形式就是 [right, right],或者带个具体的数字进去 [2, 2],这时候搜索区间非空,还有一个数 2,但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了,索引 2 没有被搜索,如果这时候直接返回 -1 就可能出现错误。 当然,如果你非要用 while(left < right) 也可以,我们已经知道了出错的原因,就打个补丁好了: 2. 为什么 left = mid + 1,right = mid - 1?我看有的代码是 right = mid 或者 left = mid,没有这些加加减减,到底怎么回事,怎么判断? 答:刚才明确了「搜索区间」这个概念,而且本算法的搜索区间是两端都闭的,即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时,如何确定下一步的搜索区间呢? 当然是去搜索 [left, mid - 1] 或者 [mid + 1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。 3. 此算法有什么缺陷? 答:至此,你应该已经掌握了该算法的所有细节,以及这样处理的原因。但是,这个算法存在局限性。 比如说给你有序数组 nums = [1,2,2,2,3],target = 2,此算法返回的索引是 2,没错。但是如果我想得到 target 的左侧边界,即索引 1,或者我想得到 target 的右侧边界,即索引 3,这样的话此算法是无法处理的。 这样的需求很常见。你也许会说,找到一个 target 索引,然后向左或向右线性搜索不行吗?可以,但是不好,因为这样难以保证二分查找对数级的时间复杂度了。 我们后续的算法就来讨论这两种二分查找的算法。 1. 为什么 while(left < right) 而不是 <= ?** 答:用相同的方法分析,因为初始化 right = nums.length 而不是 nums.length - 1 。因此每次循环的「搜索区间」是 [left, right) 左闭右开。 while(left < right) 终止的条件是 left == right,此时搜索区间 [left, left) 恰巧为空,所以可以正确终止。 2. 为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办? 答:因为要一步一步来,先理解一下这个「左侧边界」有什么特殊含义: 对于这个数组,算法会返回 1。这个 1 的含义可以这样解读:nums 中小于 2 的元素有 1 个。 比如对于有序数组 nums = [2,3,5,7], target = 1,算法会返回 0,含义是:nums 中小于 1 的元素有 0 个。如果 target = 8,算法会返回 4,含义是:nums 中小于 8 的元素有 4 个。 综上可以看出,函数的返回值(即 left 变量的值)取值区间是闭区间 [0, nums.length],所以我们简单添加两行代码就能在正确的时候 return -1: 3. 为什么 left = mid + 1,right = mid ?和之前的算法不一样? 答:这个很好解释,因为我们的「搜索区间」是 [left, right) 左闭右开,所以当 nums[mid] 被检测之后,下一步的搜索区间应该去掉 mid 分割成两个区间,即 [left, mid) 或 [mid + 1, right)。 4. 为什么该算法能够搜索左侧边界? 答:关键在于对于 nums[mid] == target 这种情况的处理: 可见,找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid) 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。 5. 为什么返回 left 而不是 right? 答:返回left和right都是一样的,因为 while 终止的条件是 left == right。 6、能不能想办法把 答: 因为搜索区间是两端都闭的,且现在是搜索左侧边界,所以 由于 while 的退出条件是 因此,最后返回结果的代码应该检查越界情况: 寻找右侧边界和寻找左侧边界的代码差不多,只有两处不同,已标注: 1. 为什么这个算法能够找到右侧边界? 答:类似地,关键点还是这里: 当 nums[mid] == target 时,不要立即返回,而是增大「搜索区间」的下界 left,使得区间不断向右收缩,达到锁定右侧边界的目的。 2. 为什么最后返回 left - 1 而不像左侧边界的函数,返回 left?而且我觉得这里既然是搜索右侧边界,应该返回 right 才对。 答:首先,while 循环的终止条件是 left == right,所以 left 和 right 是一样的,你非要体现右侧的特点,返回 right - 1 好了。 至于为什么要减一,这是搜索右侧边界的一个特殊点,关键在这个条件判断: 因为我们对 left 的更新必须是 left = mid + 1,就是说 while 循环结束时,nums[left] 一定不等于target 了,而 nums[left - 1]可能是target。 3. 为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办? 答:类似之前的左侧边界搜索,因为 while 的终止条件是 left == right,就是说 left 的取值范围是 [0, nums.length],所以可以添加两行代码,正确地返回 -1: 4、是否也可以把这个算法的「搜索区间」也统一成两端都闭的形式呢?这样这三个写法就完全统一了,以后就可以闭着眼睛写出来了。 答:当然可以,类似搜索左侧边界的统一写法,其实只要改两个地方就行了: 先来梳理一下这些细节差异的因果逻辑: 第一个,最基本的二分查找算法: 第二个,寻找左侧边界的二分查找: 第三个,寻找右侧边界的二分查找: 1. 分析二分查找代码时,不要出现 else,全部展开成 else if 方便理解。 2. 注意「搜索区间」和 while 的终止条件,如果存在漏掉的元素,记得在最后检查。 3. 如需要搜索左右边界,只要在 nums[mid] == target 时做修改即可。搜索右侧时需要减一。 当我们将区间**[l,r]划分成[l,mid]和[mid+1,r]**时,其更新操作是r = mid或者l = mid + 1,计算mid时不需要加1,即mid = (l + r)/2。 当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或者l = mid,此时为了防止死循环,计算mid时需要加1,即mid = ( l + r + 1 ) /2。 为什么模板要取while( l < r),而不是while( l <= r)? 本质上取l < r和 l <= r是没有任何区别的,只是习惯问题,如果取l <= r,只需要修改对应的更新区间即可。 while循环结束条件是l >= r,但为什么二分结束时我们优先取r而不是l? 二分的while循环的结束条件是l >= r,所以在循环结束时l有可能会大于r,此时就可能导致越界,因此,基本上二分问题优先取r都不会翻车。 整数数组 在传递给函数之前, 给你 旋转后 的数组 旋转数组即原来是一个升序数组,通过几次旋转变成一个新数组。 循环退出条件:转换为寻找一个数条件:left<=right || target=nums[mid] 二分法确定区间,该数组为两个升序数组组合而成,mid可能是第一个升序数组的值也可能是第二个升序数组的值。 通过一分为二只可能有一部分为升序数组,通过确定的一部分来调整区间位置 ①:mid是第一个升序数组的值: 判断target: target在mid前面即 nums[0] 其他情况则说明在后面区间为[mid+1,right] ②:mid是第二个升序数组的值: 判断target: target在mid后面即nums[mid] 其他情况说明在前面区间为[left,mid-1] 给定一个按照升序排列的整数数组 如果数组中不存在目标值 查找该数的左边界和右边界 方法一: 利用左右边界模板进行左右边界查询,在过程中需要判断该数是否存在以及数组是否越界 方法二 较方法一的优点:不需要判断数组越界问题 第一次查找起始位置: 第二次查找结束位置: 编写一个高效的算法来判断 方法一:一行一行往下找 方法二:上下同时找 right为最后一个数,先确定行数,在确定列数 方法三:将二维矩阵转换为一维矩阵 峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 你可以假设 你必须实现时间复杂度为 证明 1:对于任意数组而言,一定存在峰值(一定有解) 根据题意,我们有「数据长度至少为 1」、「越过数组两边看做负无穷」和「相邻元素不相等」的起始条件。 我们可以根据数组长度是否为 1 进行分情况讨论: 数组长度为 1,由于边界看做负无穷,此时峰值为该唯一元素的下标; 数组长度大于 1,从最左边的元素 **nums[0]**开始出发考虑: 如果 nums[0] > nums[1],那么最左边元素 nums[0] 就是峰值(结合左边界为负无穷); 证明 2 :二分不会错过峰值 其实基于「证明 1」,我们很容易就可以推理出「证明 2」的正确性。 整理一下由「证明 1」得出的推理:如果当前位置大于其左边界或者右边界,那么在当前位置的右边或左边必然存在峰值。 换句话说,对于一个满足 nums[x] > nums[x - 1] 的位置,x的右边一定存在峰值;或对于一个满足 nums[x] > nums[x + 1]的位置,x 的左边一定存在峰值。 (归纳为爬坡法,往数值大的方向走) 因此这里的「二段性」其实是指:在以 mid为分割点的数组上,根据 nums[mid]与 nums[mid±1] 的大小关系,可以确定其中一段满足「必然有解」,另外一段不满足「必然有解」(可能有解,可能无解)。 至此,我们证明了始终选择大于边界一端进行二分,可以确保选择的区间一定存在峰值,并随着二分过程不断逼近峰值位置。 到达数组最右侧,还没出现 nums[i] > nums[i + 1],说明数组严格递增。此时结合右边界可以看做负无穷,可判定nums[n−1] 为峰值。 综上,我们证明了无论何种情况,数组必然存在峰值。 证明 2 :二分不会错过峰值 其实基于「证明 1」,我们很容易就可以推理出「证明 2」的正确性。 整理一下由「证明 1」得出的推理:如果当前位置大于其左边界或者右边界,那么在当前位置的右边或左边必然存在峰值。 换句话说,对于一个满足 nums[x] > nums[x - 1] 的位置,x的右边一定存在峰值;或对于一个满足 nums[x] > nums[x + 1]的位置,x 的左边一定存在峰值。 (归纳为爬坡法,往数值大的方向走) 因此这里的「二段性」其实是指:在以 mid为分割点的数组上,根据 nums[mid]与 nums[mid±1] 的大小关系,可以确定其中一段满足「必然有解」,另外一段不满足「必然有解」(可能有解,可能无解)。 至此,我们证明了始终选择大于边界一端进行二分,可以确保选择的区间一定存在峰值,并随着二分过程不断逼近峰值位置。3、优缺点
4、二分查找常用场景
5、二分查找常用框架
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}
二.基本寻找与左右边界
1.寻找一个数(最基本)
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) { // 注意
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
注意点(细节)分析
if(nums[mid] == target)
return mid;
//...
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;
2、寻找左侧边界的二分搜索
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length; // 注意
while (left < right) { // 注意
int mid = (left + right) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid; // 注意
}
}
return left;
}
注意点(细节)分析
while (left < right) {
//...
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;
if (nums[mid] == target)
right = mid;
right 变成 nums.length - 1,也就是继续使用两边都闭的「搜索区间」?这样就可以和第一种二分搜索在某种程度上统一起来了。right 应该初始化为 nums.length - 1,while 的终止条件应该是 left == right + 1,也就是其中应该用 <=:int left_bound(int[] nums, int target) {
// 搜索区间为 [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}
left 和 right 的更新逻辑如下:if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
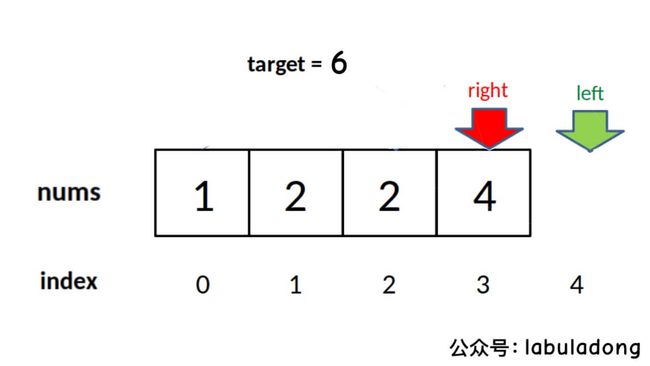
left == right + 1,所以当 target 比 nums 中所有元素都大时,会存在以下情况使得索引越界:if (left >= nums.length || nums[left] != target)
return -1;
return left;
3、寻找右侧边界的二分查找
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
left = mid + 1; // 注意
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1; // 注意
注意点(细节)分析
if (nums[mid] == target) {
left = mid + 1;
if (nums[mid] == target) {
left = mid + 1;
// 这样想: mid = left - 1
while (left < right) {
// ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这里改成收缩左侧边界即可
left = mid + 1;
}
}
// 这里改为检查 right 越界的情况,见下图
if (right < 0 || nums[right] != target)
return -1;
return right;
}
三、算法分析总结
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid+1 和 right = mid
因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid+1 和 right = mid
因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界
又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right,必须减一
**注意注意:
四、优化简洁思路模板(通用)
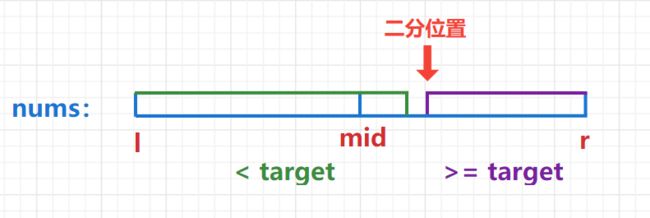
1)模板一:用来求左值–右边界更新要向下取整
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = (r + l)/2;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
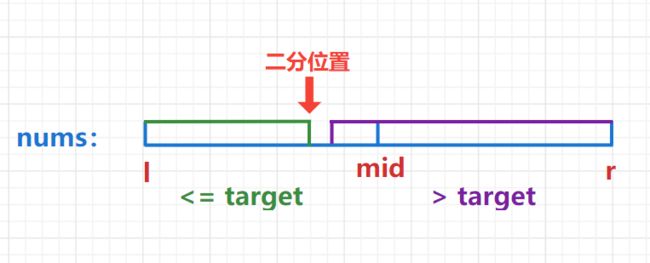
2)模板二:求右值–左边界更新要向上取整
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = ( l + r + 1 ) /2;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
3)相关问题:
四:力扣经典题分析
33. 搜索旋转排序数组
nums 按升序排列,数组中的值 互不相同 。nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
1)题目分析:
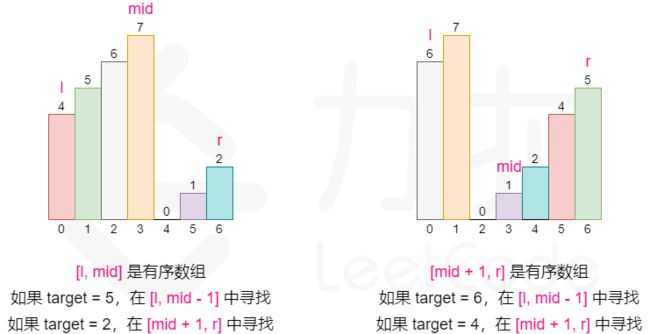
将数组一分为二,其中一定有一个是有序的,另一个可能是有序,也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二,其中一个一定有序,另一个可能有序,可能无序。就这样循环.
2)思路分析:
class Solution {
public int search(int[] nums, int target) {
if(nums.length==0){
return -1;
}
int n = nums.length;
int left = 0;
int right = n-1;
if(n==1){
return nums[0]==target?0:-1;
}
while(left<=right){
int mid = (right-left)/2+left;
if(nums[mid] == target){
return mid;
}
if(nums[0] <= nums[mid]){
if(target<nums[mid] && target>=nums[0]){
right = mid-1;
}else{
left = mid+1;
}
}
else {
if(target>nums[mid] && target<=nums[n-1]){
left = mid+1;
}else{
right = mid-1;
}
}
}
return -1;
}
}
34. 在排序数组中查找元素的第一个和最后一个位置
nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。target,返回 [-1, -1]。输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
1)题目分析:
2)思路分析:
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums.length == 0) return new int[]{-1,-1};
if(nums.length == 1 && nums[0]!=target) return new int[]{-1,-1};
if(nums.length == 1 && nums[0]==target) return new int[]{0,0};
int first = -1;
int last = -1;
int left = 0;
int right = nums.length;
//寻找左边界
while(left < right){
int mid = (right - left)/2 +left;
if(nums[mid] == target){
right = mid;
}else if(nums[mid]>target){
right = mid;
}else if(nums[mid]<target){
left = mid+1;
}
}
//一定要判断是否越界
if(left<nums.length){
first = nums[left]==target?left: -1;
}
left = 0;
right = nums.length;
//寻找右边界
while(left < right){
int mid = (right - left)/2 +left;
if(nums[mid] == target){
left = mid+1;
}else if(nums[mid]>target){
right = mid;
}else if(nums[mid]<target){
left = mid+1;
}
}
//一定要判断是否越界
if(left>0){
last = nums[left-1]==target?left-1: -1;
}
return new int[]{first,last};
}
}
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums.length == 0) return new int[]{-1,-1};
int l = 0, r = nums.length - 1;
// 模板一:用来求左值--右边界更新要向下取整
while( l < r) //查找元素的开始位置
{
int mid = (l + r )/2;
if(nums[mid] >= target) r = mid;
else l = mid + 1;
}
if( nums[r] != target) return new int[]{-1,-1}; //查找失败
int L = r;
l = 0; r = nums.length - 1;
//模板二:求右值--左边界更新要向上取整
while( l < r) //查找元素的结束位置
{
int mid = (l + r + 1)/2;
if(nums[mid] <= target ) l = mid;
else r = mid - 1;
}
return new int[]{L,r};
}
}
74. 搜索二维矩阵
m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
1)思路分析:
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row = matrix.length;
int col = matrix[0].length;
int left = 0;
int right = col-1;
int i = 0;
if(row==1 && col==1){
return target==matrix[0][0];
}
while(i<row){
int mid = (right - left)/2 + left;
if(target<matrix[i][left]){
return false;
}else if(target>matrix[i][right]){
i++;
continue;
}else{
while(left<=right){
mid = (right - left)/2 + left;
if(target==matrix[i][mid]){
return true;
}if(target<matrix[i][mid]){
right=mid-1;
}else{
left=mid+1;
}
}
return false;
}
}
return false;
}
}
class Solution {
public boolean searchMatrix(int[][] mat, int t) {
int m = mat.length, n = mat[0].length;
// 第一次二分:定位到所在行(从上往下,找到最后一个满足 mat[x]][0] <= t 的行号)
int l = 0, r = m - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
//为啥要加1,如果不加1会出现死循环(比如l = 2, r = 3的时候,如果不加1,在满足l = mid的情况下,会一直死循环),要注意二分while条件里 l < r的两种情况
if (mat[mid][0] <= t) {
l = mid;
} else {
r = mid - 1;
}
}
int row = r;
if (mat[row][0] == t) return true;
if (mat[row][0] > t) return false;
// 第二次二分:从所在行中定位到列(从左到右,找到最后一个满足 mat[row][x] <= t 的列号)
l = 0; r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[row][mid] <= t) {
l = mid;
} else {
r = mid - 1;
}
}
int col = r;
return mat[row][col] == t;
}
}
class Solution {
public boolean searchMatrix(int[][] mat, int t) {
int m = mat.length, n = mat[0].length;
int l = 0, r = m * n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (mat[mid / n][mid % n] <= t) {
l = mid;
} else {
r = mid - 1;
}
}
return mat[r / n][r % n] == t;
}
}
162. 寻找峰值
nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。nums[-1] = nums[n] = -∞ 。O(log n) 的算法来解决此问题。输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
思路分析:
如果 nums[0] < nums[1],由于已经存在明确的 nums[0] 和 nums[1]大小关系,我们将nums[0] 看做边界, nums[1] 看做新的最左侧元素,继续往右进行分析:
如果在到达数组最右侧前,出现 nums[i] > nums[i + 1],说明存在峰值位置 i(当我们考虑到nums[i],必然满足 nums[i] 大于前一元素的前提条件,当然前一元素可能是原始左边界);
到达数组最右侧,还没出现 nums[i] > nums[i + 1],说明数组严格递增。此时结合右边界可以看做负无穷,可判定nums[n−1] 为峰值。
综上,我们证明了无论何种情况,数组必然存在峰值。class Solution {
public int findPeakElement(int[] nums) {
int n = nums.length;
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] > nums[mid + 1]) r = mid;
else l = mid + 1;
}
return r;
}
}
class Solution {
public int findPeakElement(int[] nums) {
int n = nums.length;
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] > nums[mid + 1]) r = mid;
else l = mid + 1;
}
return r;
}
}