m0_62051873

python数据分析初学

PYTHON数据分析小白学习

1.numpy

接下面将从这5个方面来介绍numpy模块的内容：

1）数组的创建

2）有关数组的属性和函数

3）数组元素的获取–普通索引、切片、布尔索引和花式索引

4）统计函数与线性代数运算

5）随机数的生成

1.1数组的创建
一维数组的创建

可以使用numpy中的arange()函数创建一维有序数组，它是内置函数range的扩展版。
In 1: import numpy as np

In 2: ls1 = range(10)

In 3: list(ls1)

Out3: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

In 4: type(ls1)

Out4: range

In [5]: ls2 = np.arange(10)

In [6]: list(ls2)

Out[6]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

In [7]: type(ls2)

Out[7]: numpy.ndarray

通过arange生成的序列就不是简简单单的列表类型了，而是一个一维数组。
如果一维数组不是一个规律的有序元素，而是人为的输入，就需要array()函数创建了。

In [8]: arr1 = np.array((1,20,13,28,22))

In [9]: arr1

Out[9]: array([ 1, 20, 13, 28, 22])

In [10]: type(arr1)

Out[10]: numpy.ndarray

上面是由元组序列构成的一维数组。

In [11]: arr2 = np.array([1,1,2,3,5,8,13,21])

In [12]: arr2

Out[12]: array([ 1, 1, 2, 3, 5, 8, 13, 21])

In [13]: type(arr2)

Out[13]: numpy.ndarray

上面是由列表序列构成的一维数组。

二维数组的创建

二维数组的创建，其实在就是列表套列表或元组套元组。

In [14]: arr3 = np.array(((1,1,2,3),(5,8,13,21),(34,55,89,144)))

In [15]: arr3

Out[15]:

array([[ 1, 1, 2, 3],

[ 5, 8, 13, 21],

[ 34, 55, 89, 144]])

上面使用元组套元组的方式。

In [16]: arr4 = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])

In [17]: arr4

Out[17]:

array([[ 1, 2, 3, 4],

[ 5, 6, 7, 8],

[ 9, 10, 11, 12]])

上面使用列表套列表的方式。

对于高维数组在将来的数据分析中用的比较少，这里关于高维数组的创建就不赘述了，构建方法仍然是套的方式。
上面所介绍的都是人为设定的一维、二维或高维数组，numpy中也提供了几种特殊的数组，它们是：

In [18]: np.ones(3) #返回一维元素全为1的数组

Out[18]: array([ 1., 1., 1.])

In [19]: np.ones([3,4]) #返回元素全为1的3×4二维数组

Out[19]:

array([[ 1., 1., 1., 1.],

[ 1., 1., 1., 1.],

[ 1., 1., 1., 1.]])

In [20]: np.zeros(3) #返回一维元素全为0的数组

Out[20]: array([ 0., 0., 0.])

In [21]: np.zeros([3,4]) #返回元素全为0的3×4二维数组

Out[21]:

array([[ 0., 0., 0., 0.],

[ 0., 0., 0., 0.],

[ 0., 0., 0., 0.]])

In [22]: np.empty(3) #返回一维空数组

Out[22]: array([ 0., 0., 0.])

In [23]: np.empty([3,4]) #返回3×4二维空数组

Out[23]:

array([[ 0., 0., 0., 0.],

[ 0., 0., 0., 0.],

[ 0., 0., 0., 0.]])

1.2有关数组的属性和函数

In [25]: arr3.shape #shape方法返回数组的行数和列数

Out[25]: (3, 4)

In [26]: arr3.dtype #dtype方法返回数组的数据类型

Out[26]: dtype(‘int32’)

拉直办法

In [27]: a = arr3.ravel() #通过ravel的方法将数组拉直（多维数组降为一维数组）

In [28]: a

Out[28]: array([ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144])

In [29]: b = arr3.flatten() #通过flatten的方法将数组拉直

In [30]: b

Out[30]: array([ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144])

两者的区别在于ravel方法生成的是原数组的视图，无需占有内存空间，但视图的改变会影响到原数组的变化。而flatten方法返回的是真实值，其值的改变并不会影响原数组的更改。
拉直两种方法例子比较：
通过下面的例子也许就能明白了：

In [31]: b[:3] = 0

In [32]: arr3

Out[32]:

array([[ 1, 1, 2, 3],

[ 5, 8, 13, 21],

[ 34, 55, 89, 144]])

通过更改b的值，原数组没有变化。（fatten）

In [33]: a[:3] = 0

In [34]: arr3

Out[34]:

array([[ 0, 0, 0, 3],

[ 5, 8, 13, 21],

[ 34, 55, 89, 144]])

a的值变化后，会导致原数组跟着变化。（ravel）

In [35]: arr4

Out[35]:

array([[ 1, 2, 3, 4],

[ 5, 6, 7, 8],

[ 9, 10, 11, 12]])

In [36]: arr4.ndim #返回数组的维数

Out[36]: 2

In [37]: arr4.size #返回数组元素的个数

Out[37]: 12
In [38]: arr4.T #返回数组的转置结果

Out[38]:

array([[ 1, 5, 9],

[ 2, 6, 10],

[ 3, 7, 11],

[ 4, 8, 12]])

如果数组的数据类型为复数的话，real方法可以返回复数的实部，imag方法返回复数的虚部。
介绍完数组的一些方法后，接下来我们看看数组自身有哪些函数可操作：

In [39]: len(arr4) #返回数组有多少行

Out[39]: 3

In [40]: arr3

Out[40]:

array([[ 0, 0, 0, 3],

[ 5, 8, 13, 21],

[ 34, 55, 89, 144]])

In [41]: arr4

Out[41]:

array([[ 1, 2, 3, 4],

[ 5, 6, 7, 8],

[ 9, 10, 11, 12]])

In [42]: np.hstack((arr3,arr4))

Out[42]:

array([[ 0, 0, 0, 3, 1, 2, 3, 4],

[ 5, 8, 13, 21, 5, 6, 7, 8],

[ 34, 55, 89, 144, 9, 10, 11, 12]])

横向拼接arr3和arr4两个数组，但必须满足两个数组的行数相同。

In [43]: np.vstack((arr3,arr4))

Out[43]:

array([[ 0, 0, 0, 3],

[ 5, 8, 13, 21],

[ 34, 55, 89, 144],

[ 1, 2, 3, 4],

[ 5, 6, 7, 8],

[ 9, 10, 11, 12]])

纵向拼接arr3和arr4两个数组，但必须满足两个数组的列数相同。

In [44]: np.column_stack((arr3,arr4)) #与hstack函数具有一样的效果

Out[44]:

array([[ 0, 0, 0, 3, 1, 2, 3, 4],

[ 5, 8, 13, 21, 5, 6, 7, 8],

[ 34, 55, 89, 144, 9, 10, 11, 12]])

In [45]: np.row_stack((arr3,arr4)) #与vstack函数具有一样的效果

Out[45]:

array([[ 0, 0, 0, 3],

[ 5, 8, 13, 21],

[ 34, 55, 89, 144],

[ 1, 2, 3, 4],

[ 5, 6, 7, 8],

[ 9, 10, 11, 12]])

reshape()函数和resize()函数可以重新设置数组的行数和列数：

In [46]: arr5 = np.array(np.arange(24))

In [47]: arr5 #此为一维数组

Out[47]:

array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,

17, 18, 19, 20, 21, 22, 23])

In [48]: a = arr5.reshape(4,6)

In [49]: a

Out[49]:

array([[ 0, 1, 2, 3, 4, 5],

[ 6, 7, 8, 9, 10, 11],

[12, 13, 14, 15, 16, 17],

[18, 19, 20, 21, 22, 23]])

通过reshape函数将一维数组设置为二维数组，且为4行6列的数组。

In [50]: a.resize(6,4)

In [51]: a

Out[51]:

array([[ 0, 1, 2, 3],

[ 4, 5, 6, 7],

[ 8, 9, 10, 11],

[12, 13, 14, 15],

[16, 17, 18, 19],

[20, 21, 22, 23]])

通过resize函数会直接改变原数组的形状。

数组转换：tolist将数组转换为列表，astype()强制转换数组的数据类型，下面是两个函数的例子：

In [53]: b = a.tolist()

In [54]: b

Out[54]:

[[0, 1, 2, 3],

[4, 5, 6, 7],

[8, 9, 10, 11],

[12, 13, 14, 15],

[16, 17, 18, 19],

[20, 21, 22, 23]]

In [55]: type(b)

Out[55]: list

In [56]: c = a.astype(float)

In [57]: c

Out[57]:

array([[ 0., 1., 2., 3.],

[ 4., 5., 6., 7.],

[ 8., 9., 10., 11.],

[ 12., 13., 14., 15.],

[ 16., 17., 18., 19.],

[ 20., 21., 22., 23.]])

In [58]: a.dtype

Out[58]: dtype(‘int32’)

In [59]: c.dtype

Out[59]: dtype(‘float64’)

1.3 数组元素的获取

通过索引和切片的方式获取数组元素，一维数组元素的获取与列表、元组的获取方式一样：
In [60]: arr7 = np.array(np.arange(10))

In [61]: arr7

Out[61]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [62]: arr73 #获取第4个元素

Out[62]: 3

In [63]: arr7[:3] #获取前3个元素

Out[63]: array([0, 1, 2])

In [64]: arr7[3:] #获取第4个元素即之后的所有元素

Out[64]: array([3, 4, 5, 6, 7, 8, 9])

In [65]: arr7[-2:] #获取末尾的2个元素

Out[65]: array([8, 9])

In [66]: arr7[::2] #从第1个元素开始，获取步长为2的所有元素

Out[66]: array([0, 2, 4, 6, 8])

二维数组元素的获取：

In [67]: arr8 = np.array(np.arange(12)).reshape(3,4)

In [68]: arr8

Out[68]:

array([[ 0, 1, 2, 3],

[ 4, 5, 6, 7],

[ 8, 9, 10, 11]])

In [69]: arr81 #返回数组的第2行

Out[69]: array([4, 5, 6, 7])

In [70]: arr8[:2] #返回数组的前2行

Out[70]:

array([[0, 1, 2, 3],

[4, 5, 6, 7]])

In [71]: arr8[[0,2]] #返回指定的第1行和第3行

Out[71]:

array([[ 0, 1, 2, 3],

[ 8, 9, 10, 11]])

In [72]: arr8[:,0] #返回数组的第1列

Out[72]: array([0, 4, 8]

In [73]: arr8[:,-2:] #返回数组的后2列

Out[73]:

array([[ 2, 3],

[ 6, 7],

[10, 11]])

In [74]: arr8[:,[0,2]] #返回数组的第1列和第3列

Out[74]:

array([[ 0, 2],

[ 4, 6],

[ 8, 10]])

In [75]: arr8[1,2] #返回数组中第2行第3列对应的元素

Out[75]: 6

布尔索引，即索引值为True和False，需要注意的是布尔索引必须输数组对象。
In [76]: log = np.array([True,False,False,True,True,False])

In [77]: arr9 = np.array(np.arange(24)).reshape(6,4)

In [78]: arr9

Out[78]:

array([[ 0, 1, 2, 3],

[ 4, 5, 6, 7],

[ 8, 9, 10, 11],

[12, 13, 14, 15],

[16, 17, 18, 19],

[20, 21, 22, 23]])

In [79]: arr9[log] #返回所有为True的对应行

Out[79]:

array([[ 0, 1, 2, 3],

[12, 13, 14, 15],

[16, 17, 18, 19]])

In [80]: arr9[-log] #通过负号筛选出所有为False的对应行

Out[80]:

array([[ 4, 5, 6, 7],

[ 8, 9, 10, 11],

[20, 21, 22, 23]])

举一个场景，一维数组表示区域，二维数组表示观测值，如何选取目标区域的观测？
In [81]: area = np.array([‘A’,‘B’,‘A’,‘C’,‘A’,‘B’,‘D’])

In [82]: area

Out[82]:

array([‘A’, ‘B’, ‘A’, ‘C’, ‘A’, ‘B’, ‘D’],

dtype=’

In [83]: observes = np.array(np.arange(21)).reshape(7,3)

In [84]: observes

Out[84]:

array([[ 0, 1, 2],

[ 3, 4, 5],

[ 6, 7, 8],

[ 9, 10, 11],

[12, 13, 14],

[15, 16, 17],

[18, 19, 20]])

In [85]: observes[area == ‘A’]

Out[85]:

array([[ 0, 1, 2],

[ 6, 7, 8],

[12, 13, 14]])

返回所有A区域的观测。

In [86]: observes[(area == ‘A’) | (area == ‘D’)] #条件值需要在&(and),|(or)两端用圆括号括起来
Out[86]:
array([[ 0, 1, 2],
[ 6, 7, 8],
[12, 13, 14],
[18, 19, 20]])
返回所有A区域和D区域的观测。

当然，布尔索引也可以与普通索引或切片混合使用：

In [87]: observes[area == ‘A’][:,[0,2]]

Out[87]:

array([[ 0, 2],

[ 6, 8],

[12, 14]])

返回A区域的所有行，且只获取第1列与第3列数据。

花式索引：实际上就是将数组作为索引将原数组的元素提取出来
n [88]: arr10 = np.arange(1,29).reshape(7,4)

In [89]: arr10

Out[89]:

array([[ 1, 2, 3, 4],

[ 5, 6, 7, 8],

[ 9, 10, 11, 12],

[13, 14, 15, 16],

[17, 18, 19, 20],

[21, 22, 23, 24],

[25, 26, 27, 28]])

In [90]: arr10[[4,1,3,5]] #按照指定顺序返回指定行

Out[90]:

array([[17, 18, 19, 20],

[ 5, 6, 7, 8],

[13, 14, 15, 16],

[21, 22, 23, 24]])

In [91]: arr10[[4,1,5]][:,[0,2,3]] #返回指定的行与列

Out[91]:

array([[17, 19, 20],

[ 5, 7, 8],

[21, 23, 24]])

In [92]: arr10[[4,1,5],[0,2,3]]

Out[92]: array([17, 7, 24]
请注意！这与上面的返回结果是截然不同的，上面返回的是二维数组，而这条命令返回的是一维数组。

如果想使用比较简单的方式返回指定行以列的二维数组的话，可以使用ix_()函数
In [93]: arr10[np.ix_([4,1,5],[0,2,3])]

Out[93]:

array([[17, 19, 20],

[ 5, 7, 8],

[21, 23, 24]])

这与arr10[[4,1,5]][:,[0,2,3]]返回的结果是一致的。

1.4统计函数与线性代数运算

统计运算中常见的聚合函数有：最小值、最大值、中位数、均值、方差、标准差等。首先来看看数组元素级别的计算：
In [94]: arr11 = 5-np.arange(1,13).reshape(4,3)

In [95]: arr12 = np.random.randint(1,10,size = 12).reshape(4,3)
In [96]: arr11

Out[96]:

array([[ 4, 3, 2],

[ 1, 0, -1],

[-2, -3, -4],

[-5, -6, -7]])

In [97]: arr12

Out[97]:

array([[1, 3, 7],

[7, 3, 7],

[3, 7, 4],

[6, 1, 2]])

In [98]: arr11 ** 2 #计算每个元素的平方

Out[98]:

array([[16, 9, 4],

[ 1, 0, 1],

[ 4, 9, 16],

[25, 36, 49]])

In [99]: np.sqrt(arr11) #计算每个元素的平方根

Out[99]:

array([[ 2. , 1.73205081, 1.41421356],

[ 1. , 0. , nan],

[ nan, nan, nan],

[ nan, nan, nan]])
由于负值的平方根没有意义，故返回nan。

In [100]: np.exp(arr11) #计算每个元素的指数值

Out[100]:

array([[ 5.45981500e+01, 2.00855369e+01, 7.38905610e+00],

[ 2.71828183e+00, 1.00000000e+00, 3.67879441e-01],

[ 1.35335283e-01, 4.97870684e-02, 1.83156389e-02],

[ 6.73794700e-03, 2.47875218e-03, 9.11881966e-04]])

In [101]: np.log(arr12) #计算每个元素的自然对数值

Out[101]:

array([[ 0. , 1.09861229, 1.94591015],

[ 1.94591015, 1.09861229, 1.94591015],

[ 1.09861229, 1.94591015, 1.38629436],

[ 1.79175947, 0. , 0.69314718]])

In [102]: np.abs(arr11) #计算每个元素的绝对值

Out[102]:

array([[4, 3, 2],

[1, 0, 1],

[2, 3, 4],

[5, 6, 7]]
相同形状数组间元素的操作：

In [103]: arr11 + arr12 #加

Out[103]:

array([[ 5, 6, 9],

[ 8, 3, 6],

[ 1, 4, 0],

[ 1, -5, -5]])

In [104]: arr11 - arr12 #减

Out[104]:

array([[ 3, 0, -5],

[ -6, -3, -8],

[ -5, -10, -8],

[-11, -7, -9]])

In [105]: arr11 * arr12 #乘

Out[105]:

array([[ 4, 9, 14],

[ 7, 0, -7],

[ -6, -21, -16],

[-30, -6, -14]])

In [106]: arr11 / arr12 #除

Out[106]:

array([[ 4. , 1. , 0.28571429],

[ 0.14285714, 0. , -0.14285714],

[-0.66666667, -0.42857143, -1. ],

[-0.83333333, -6. , -3.5 ]])

In [107]: arr11 // arr12 #整除

Out[107]:

array([[ 4, 1, 0],

[ 0, 0, -1],

[-1, -1, -1],

[-1, -6, -4]], dtype=int32)

In [108]: arr11 % arr12 #取余

Out[108]:

array([[0, 0, 2],

[1, 0, 6],

[1, 4, 0],

[1, 0, 1]], dtype=int32)

接下来我们看看统计运算函数：

In [109]: np.sum(arr11) #计算所有元素的和

Out[109]: -18

In [110]: np.sum(arr11,axis = 0) #对每一列求和

Out[110]: array([ -2, -6, -10])

In [111]: np.sum(arr11, axis = 1) #对每一行求和

Out[111]: array([ 9, 0, -9, -18])

In [112]: np.cumsum(arr11) #对每一个元素求累积和（从上到下，从左到右的元素顺序）
Out[112]: array([ 4, 7, 9, 10, 10, 9, 7, 4, 0, -5, -11, -18], dtype=int32

In [113]: np.cumsum(arr11, axis = 0) #计算每一列的累积和，并返回二维数组

Out[113]:

array([[ 4, 3, 2],

[ 5, 3, 1],

[ 3, 0, -3],

[ -2, -6, -10]], dtype=int32)

In [114]: np.cumprod(arr11, axis = 1) #计算每一行的累计积，并返回二维数组

Out[114]:

array([[ 4, 12, 24],

[ 1, 0, 0],

[ -2, 6, -24],

[ -5, 30, -210]], dtype=int32)

In [115]: np.min(arr11) #计算所有元素的最小值

Out[115]: -7

In [116]: np.max(arr11, axis = 0) #计算每一列的最大值

Out[116]: array([4, 3, 2])

In [117]: np.mean(arr11) #计算所有元素的均值

Out[117]: -1.5

In [118]: np.mean(arr11, axis = 1) #计算每一行的均值

Out[118]: array([ 3., 0., -3., -6.])

In [119]: np.median(arr11) #计算所有元素的中位数

Out[119]: -1.5

In [120]: np.median(arr11, axis = 0) #计算每一列的中位数

Out[120]: array([-0.5, -1.5, -2.5])

In [121]: np.var(arr12) #计算所有元素的方差

Out[121]: 5.354166666666667

In [122]: np.std(arr12, axis = 1) #计算每一行的标准差

Out[122]: array([ 2.49443826, 1.88561808, 1.69967317, 2.1602469 ])

numpy中的统计函数运算是非常灵活的，既可以计算所有元素的统计值，也可以计算指定行或列的统计指标。还有其他常用的函数，如符号函数sign，ceil(>=x的最小整数)，floor(<=x的最大整数)，modf(将浮点数的整数部分与小数部分分别存入两个独立的数组)，cos，arccos，sin，arcsin，tan，arctan等。
让我很兴奋的一个函数是where()，它类似于Excel中的if函数，可以进行灵活的变换：
In [123]: arr11

Out[123]:

array([[ 4, 3, 2],

[ 1, 0, -1],

[-2, -3, -4],

[-5, -6, -7]])

In [124]: np.where(arr11 < 0, ‘negtive’,‘positive’)

Out[124]:

array([[‘positive’, ‘positive’, ‘positive’],

[‘positive’, ‘positive’, ‘negtive’],

[‘negtive’, ‘negtive’, ‘negtive’],

[‘negtive’, ‘negtive’, ‘negtive’]],

dtype=’

当然，np.where还可以嵌套使用，完成复杂的运算。

其它函数
unique(x):计算x的唯一元素，并返回有序结果
intersect(x,y)：计算x和y的公共元素，即交集
union1d(x,y):计算x和y的并集
setdiff1d(x,y):计算x和y的差集，即元素在x中，不在y中
setxor1d(x,y):计算集合的对称差，即存在于一个数组中，但不同时存在于两个数组中
in1d(x,y):判断x的元素是否包含于y中

线性代数运算

同样numpu也跟R语言一样，可以非常方便的进行线性代数方面的计算，如行列式、逆、迹、特征根、特征向量等。但需要注意的是，有关线性代数的函数并不在numpy中，而是numpy的子例linalg中。
In [125]: arr13 = np.array([[1,2,3,5],[2,4,1,6],[1,1,4,3],[2,5,4,1]])

In [126]: arr13

Out[126]:

array([[1, 2, 3, 5],

[2, 4, 1, 6],

[1, 1, 4, 3],

[2, 5, 4, 1]])

In [127]: np.linalg.det(arr13) #返回方阵的行列式

Out[127]: 51.000000000000021

In [128]: np.linalg.inv(arr13) #返回方阵的逆

Out[128]:

array([[-2.23529412, 1.05882353, 1.70588235, -0.29411765],

[ 0.68627451, -0.25490196, -0.7254902 , 0.2745098 ],

[ 0.19607843, -0.21568627, 0.07843137, 0.07843137],

[ 0.25490196, 0.01960784, -0.09803922, -0.09803922]])

In [129]: np.trace(arr13) #返回方阵的迹（对角线元素之和），注意迹的求解不在linalg子例程中

Out[129]: 10

In [130]: np.linalg.eig(arr13) #返回由特征根和特征向量组成的元组

Out[130]:

(array([ 11.35035004, -3.99231852, -0.3732631 , 3.01523159]),

array([[-0.4754174 , -0.48095078, -0.95004728, 0.19967185],

[-0.60676806, -0.42159999, 0.28426325, -0.67482638],

[-0.36135292, -0.16859677, 0.08708826, 0.70663129],

[-0.52462832, 0.75000995, 0.09497472, -0.07357122]]))

In [131]: np.linalg.qr(arr13) #返回方阵的QR分解

Out[131]:

(array([[-0.31622777, -0.07254763, -0.35574573, -0.87645982],

[-0.63245553, -0.14509525, 0.75789308, -0.06741999],

[-0.31622777, -0.79802388, -0.38668014, 0.33709993],

[-0.63245553, 0.580381 , -0.38668014, 0.33709993]]),

array([[-3.16227766, -6.64078309, -5.37587202, -6.95701085],

[ 0. , 1.37840488, -1.23330963, -3.04700025],

[ 0. , 0. , -3.40278524, 1.22190924],

[ 0. , 0. , 0. , -3.4384193 ]]))

In [132]:np.linalg.svd(arr13) #返回方阵的奇异值分解

Out[132]:

(array([[-0.50908395, 0.27580803, 0.35260559, -0.73514132],

[-0.59475561, 0.4936665 , -0.53555663, 0.34020325],

[-0.39377551, -0.10084917, 0.70979004, 0.57529852],

[-0.48170545, -0.81856751, -0.29162732, -0.11340459]]),

array([ 11.82715609, 4.35052602, 3.17710166, 0.31197297]),

array([[-0.25836994, -0.52417446, -0.47551003, -0.65755329],

[-0.10914615, -0.38326507, -0.54167613, 0.74012294],

[-0.18632462, -0.68784764, 0.69085326, 0.12194478],

[ 0.94160248, -0.32436807, -0.05655931, -0.07050652]]))

QR分解法
QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵。正规正交矩阵Q满足条件，所以称为QR分解法与此正规正交矩阵的通用符号Q有关。
MATLAB以qr函数来执行QR分解法，其语法为[Q,R]=qr(A)，其中Q代表正规正交矩阵，而R代表上三角形矩阵。此外，原矩阵A不必为正方矩阵；如果矩阵A大小为，则矩阵Q大小为，矩阵R大小为。
奇异值分解法
奇异值分解 (sigular value decomposition,SVD) 是另一种正交矩阵分解法；SVD是最可靠的分解法，但是它比QR 分解法要花上近十倍的计算时间。[U,S,V]=svd(A)，其中U和V代表二个相互正交矩阵，而S代表一对角矩阵。和QR分解法相同者，原矩阵A不必为正方矩阵。
使用SVD分解法的用途是解最小平方误差法和数据压缩。

1.5 随机数生成

统计学中经常会讲到数据的分布特征，如正态分布、指数分布、卡方分布、二项分布、泊松分布等，下面就讲讲有关分布的随机数生成。

正态分布直方图

In [137]: import matplotlib #用于绘图的模块

In [138]: np.random.seed(1234) #设置随机种子

In [139]: N = 10000 #随机产生的样本量

In [140]: randnorm = np.random.normal(size = N) #生成正态随机数

In [141]: counts, bins, path = matplotlib.pylab.hist(randnorm, bins = np.sqrt(N), normed = True, color = ‘blue’) #绘制直方图

以上将直方图的频数和组距存放在counts和bins内。

n [142]: sigma = 1; mu = 0

**In [143]: norm_dist = (1/np.sqrt(2sigmanp.pi))*np.exp(-((bins-mu)2)/2) 正态分布密度函数

In [144]: matplotlib.pylab.plot(bins,norm_dist,color = ‘red’) #绘制正态分布密度函数图

使用二项分布进行赌博

同时抛弃9枚硬币，如果正面朝上少于5枚，则输掉8元，否则就赢8元。如果手中有1000元作为赌资，请问赌博10000次后可能会是什么情况呢？
In [146]: np.random.seed(1234)

In [147]: binomial = np.random.binomial(9,0.5,10000) #生成二项分布随机数
In [148]: money = np.zeros(10000) #生成10000次赌资的列表
In [149]: money[0] = 1000 #首次赌资为1000元
In [150]: for i in range(1,10000):

…： if binomial[i] < 5:

 ...:         money[i] = money[i-1] - 8

#如果少于5枚正面，则在上一次赌资的基础上输掉8元

 ...:     else:

 ...:         money[i] = money[i-1] + 8

#如果至少5枚正面，则在上一次赌资的基础上赢取8元

In [151]: matplotlib.pylab.plot(np.arange(10000), money)

使用随机整数实现随机游走
一个醉汉在原始位置上行走10000步后将会在什么地方呢？如果他每走一步是随机的，即下一步可能是1也可能是-1。

In [152]: np.random.seed(1234) #设定随机种子

In [153]: position = 0 #设置初始位置

In [154]: walk = [] #创建空列表

In [155]: steps = 10000 #假设接下来行走10000步

In [156]: for i in np.arange(steps):

 ...:     step = 1 if np.random.randint(0,2) else -1  #每一步都是随机的

 ...:     position = position + step  #对每一步进行累计求和

 ...:     walk.append(position)   #确定每一步所在的位置

In [157]: matplotlib.pylab.plot(np.arange(10000), walk) #绘制随机游走图

上面的代码还可以写成（结合前面所讲的where函数，cumsum函数）：

In [158]: np.random.seed(1234)

In [159]: step = np.where(np.random.randint(0,2,10000)>0,1,-1)

In [160]: position = np.cumsum(step)

In [161]: matplotlib.pylab.plot(np.arange(10000), position)

2.pandas

2.1 前期准备

import pandas as pd

mydataset = {
‘sites’: [“Google”, “Runoob”, “Wiki”],
‘number’: [1, 2, 3]
}

myvar = pd.DataFrame(mydataset)

print(myvar)

2.2 pandas 数据结构 ——Series

Pandas Series 类似表格中的一个列（column），类似于一维数组，可以保存任何数据类型
pandas.Series( data, index, dtype, name, copy)

参数说明：

data：一组数据(ndarray 类型)。

index：数据索引标签，如果不指定，默认从 0 开始。

dtype：数据类型，默认会自己判断。

name：设置名称。

copy：拷贝数据，默认为 False。

1.import pandas as pd

a = [1, 2, 3]

myvar = pd.Series(a)

print(myvar)

2.我们可以指定索引值，如下实例：

实例
import pandas as pd

a = ["Google", "Runoob", "Wiki"]

myvar = pd.Series(a, index = ["x", "y", "z"])

print(myvar)
print(myvar["y"])
输出结果如下：

Runoob

我们也可以使用 key/value 对象，类似字典来创建 Series：

实例
import pandas as pd

sites = {1: “Google”, 2: “Runoob”, 3: “Wiki”}

myvar = pd.Series(sites)

print(myvar)
字典的 key 变成了索引值。
如果我们只需要字典中的一部分数据，只需要指定需要数据的索引即可，如下实例：
import pandas as pd

sites = {1: “Google”, 2: “Runoob”, 3: “Wiki”}

myvar = pd.Series(sites, index = [1, 2])

print(myvar)
只取前面两个
设置 Series 名称参数：

实例
import pandas as pd

sites = {1: "Google", 2: "Runoob", 3: "Wiki"}

myvar = pd.Series(sites, index = [1, 2], name="RUNOOB-Series-TEST" )

print(myvar)
**设置名字**

2.3 dataframe

DataFrame 是一个表格型的数据结构，它含有一组有序的列，每列可以是不同的值类型（数值、字符串、布尔型值）。DataFrame 既有行索引也有列索引，它可以被看做由 Series 组成的字典（共同用一个索引）。
pandas.DataFrame( data, index, columns, dtype, copy)

参数说明：

data：一组数据(ndarray、series, map, lists, dict 等类型)。

index：索引值，或者可以称为行标签。

columns：列标签，默认为 RangeIndex (0, 1, 2, …, n) 。

dtype：数据类型。

copy：拷贝数据，默认为 False。
Pandas DataFrame 是一个二维的数组结构，类似二维数组。
实例 - 使用列表创建
import pandas as pd

data = [['Google',10],['Runoob',12],['Wiki',13]]

df = pd.DataFrame(data,columns=['Site','Age'],dtype=float)

print(df)
输出结果如下：

2.还可以使用字典（key/value），其中字典的 key 为列名:
import pandas as pd

data = [{'a': 1, 'b': 2},{'a': 5, 'b': 10, 'c': 20}]

df = pd.DataFrame(data)

print (df)
    a   b     c
0  1   2   NaN
1  5  10  20.0
**没有对应的部分数据为 NaN**

3.Pandas 可以使用 loc 属性返回指定行的数据，如果没有设置索引，第一行索引为 0，第二行索引为 1，以此类推：

实例
import pandas as pd

data = {
"calories": [420, 380, 390],
 "duration": [50, 40, 45]
}

 数据载入到 DataFrame 对象
df = pd.DataFrame(data)

返回第一行
print(df.loc[0])
返回第二行
print(df.loc[1])**
返回第一行和第二行
print(df.loc[[0, 1]])
df = pd.DataFrame(data, index = ["day1", "day2", "day3"])
print(df)  #行名为day1，day2, day3
输出结果为：

  calories  duration

day1 420 50
day2 380 40
day3 390 45
#指定索引
print(df.loc[“day2”])

2.4 csv 文件

Pandas 可以很方便的处理 CSV 文件，本文以 nba.csv 为例，你可以下载 nba.csv 或打开 nba.csv 查看。
1.实例
import pandas as pd

df = pd.read_csv('nba.csv')

print(df.to_string())

to_string() 用于返回 DataFrame 类型的数据，如果不使用该函数，则输出结果为数据的前面 5 行和末尾 5 行，中间部分以 … 代替。
print(df)
2.我们也可以使用 to_csv() 方法将 DataFrame 存储为 csv 文件：

实例
import pandas as pd

#三个字段 name, site, age
nme = [“Google”, “Runoob”, “Taobao”, “Wiki”]
st = [“www.google.com”, “www.runoob.com”, “www.taobao.com”, “www.wikipedia.org”]
ag = [90, 40, 80, 98]

#字典
dict = {‘name’: nme, ‘site’: st, ‘age’: ag}

df = pd.DataFrame(dict)

#保存 dataframe
df.to_csv(‘site.csv’)
3.数据处理head()
head( n ) 方法用于读取前面的 n 行，如果不填参数 n ，默认返回 5 行。

实例 - 读取前面 5 行
import pandas as pd

df = pd.read_csv('nba.csv')

print(df.head())
print(df.head(10))

4.tail()
tail( n ) 方法用于读取尾部的 n 行，如果不填参数 n ，**默认返回 5 行，**空行各个字段的值返回 NaN。
实例 - 读取末尾 5 行
import pandas as pd

df = pd.read_csv('nba.csv')

print(df.tail())
print(df.tail(10))

5.info()
info() 方法返回表格的一些基本信息：
import pandas as pd

df = pd.read_csv('nba.csv')

print(df.info())

输出结果为：

RangeIndex: 458 entries, 0 to 457 # 行数，458 行，第一行编号为 0
Data columns (total 9 columns): # 列数，9列

Column Non-Null Count Dtype # 各列的数据类型

0 Name 457 non-null object
1 Team 457 non-null object
2 Number 457 non-null float64
3 Position 457 non-null object
4 Age 457 non-null float64
5 Height 457 non-null object
6 Weight 457 non-null float64
7 College 373 non-null object # non-null，意思为非空的数据
8 Salary 446 non-null float64
dtypes: float64(4), object(5) # 类型

2.5 JSON

JSON（JavaScript Object Notation，JavaScript 对象表示法），是存储和交换文本信息的语法，类似 XML。

JSON 比 XML 更小、更快，更易解析，更多 JSON 内容可以参考 JSON 教程。
JSON（JavaScript Object Notation）是一种轻量级的数据交换格式，可使人们很容易地进行阅读和编写，同时也方便了机器进行解析和生成。JSON适用于进行数据交互的场景，如网站前台与后台之间的数据交互。
JSON是比XML更简单的一种数据交换格式，它采用完全独立于编程语言的文本格式来存储和表示数据。
其语法规则如下：
(1)使用键值对( key:value )表示对象属性和值。
(2)使用逗号(，)分隔多条数据。
(3)使用花括号{}包含对象。
(4)使用方括号[ ]表示数组。
在JavaScript语言中，一切皆是对象，所以任何支持的类型都可以通过JSON来表示，如字符串、数字、对象、数组等。其中，对象和数组是比较特殊且常用的两种类型。
实例
import pandas as pd

df = pd.read_json(‘sites.json’)

print(df.to_string())
to_string() 用于返回 DataFrame 类型的数据，我们也可以直接处理 JSON 字符串。
import pandas as pd

#字典格式的 JSON
s = {
“col1”:{“row1”:1,“row2”:2,“row3”:3},
“col2”:{“row1”:“x”,“row2”:“y”,“row3”:“z”}
}

#读取 JSON 转为 DataFrame
df = pd.DataFrame(s)
print(df)

从 URL 中读取 JSON 数据：

实例
import pandas as pd

URL = ‘https://static.runoob.com/download/sites.json’
df = pd.read_json(URL)
print(df)
以上实例输出结果为：

 id    name            		 url 									 likes

0 A001 菜鸟教程 www.runoob.com 61
1 A002 Google www.google.com 124
2 A003 淘宝 www.taobao.com 45

内嵌的 JSON 数据
假设有一组内嵌的 JSON 数据文件 nested_list.json ：
nested_list.json 文件内容
{
“school_name”: “ABC primary school”,
“class”: “Year 1”,
“students”: [
{
“id”: “A001”,
“name”: “Tom”,
“math”: 60,
“physics”: 66,
“chemistry”: 61
},
{
“id”: “A002”,
“name”: “James”,
“math”: 89,
“physics”: 76,
“chemistry”: 51
},
{
“id”: “A003”,
“name”: “Jenny”,
“math”: 79,
“physics”: 90,
“chemistry”: 78
}]
}
使用以下代码格式化完整内容：

实例
import pandas as pd

df = pd.read_json(‘nested_list.json’)

print(df)
以上实例输出结果为：

      school_name   class                                           students

0 ABC primary school Year 1 {‘id’: ‘A001’, ‘name’: ‘Tom’, ‘math’: 60, 'phy…
1 ABC primary school Year 1 {‘id’: ‘A002’, ‘name’: ‘James’, ‘math’: 89, 'p…
2 ABC primary school Year 1 {‘id’: ‘A003’, ‘name’: ‘Jenny’, ‘math’: 79, 'p…

这时我们就需要使用到 json_normalize() 方法将内嵌的数据完整的解析出来：解析students

实例
import pandas as pd
import json

#使用 Python JSON 模块载入数据
with open(‘nested_list.json’,‘r’) as f:
data = json.loads(f.read())

#展平数据
df_nested_list = pd.json_normalize(data, record_path =[‘students’])
print(df_nested_list)
以上实例输出结果为：

 id   name  math  physics  chemistry

0 A001 Tom 60 66 61
1 A002 James 89 76 51
2 A003 Jenny 79 90 78

data = json.loads(f.read()) 使用 Python JSON 模块载入数据。

json_normalize() 使用了参数 record_path 并设置为 [‘students’] 用于展开内嵌的 JSON 数据 students。

显示结果还没有包含 school_name 和 class 元素，如果需要展示出来可以使用 meta 参数来显示这些元数据：
实例
import pandas as pd
import json

#使用 Python JSON 模块载入数据
with open(‘nested_list.json’,‘r’) as f:
data = json.loads(f.read())

#展平数据
df_nested_list = pd.json_normalize(
data,
record_path =[‘students’],
meta=[‘school_name’, ‘class’]
)
print(df_nested_list)
以上实例输出结果为：

 id   name  math  physics  chemistry         school_name   class

0 A001 Tom 60 66 61 ABC primary school Year 1
1 A002 James 89 76 51 ABC primary school Year 1
2 A003 Jenny 79 90 78 ABC primary school Year 1

接下来，让我们尝试读取更复杂的 JSON 数据，该数据嵌套了列表和字典，数据文件 nested_mix.json 如下：

nested_mix.json 文件内容
{
“school_name”: “local primary school”,
“class”: “Year 1”,
“info”: {
“president”: “John Kasich”,
“address”: “ABC road, London, UK”,
“contacts”: {
“email”: “[email protected]”,
“tel”: “123456789”
}
},
“students”: [
{
“id”: “A001”,
“name”: “Tom”,
“math”: 60,
“physics”: 66,
“chemistry”: 61
},
{
“id”: “A002”,
“name”: “James”,
“math”: 89,
“physics”: 76,
“chemistry”: 51
},
{
“id”: “A003”,
“name”: “Jenny”,
“math”: 79,
“physics”: 90,
“chemistry”: 78
}]
}
nested_mix.json 文件转换为 DataFrame：

实例
import pandas as pd
import json

#使用 Python JSON 模块载入数据
with open(‘nested_mix.json’,‘r’) as f:
data = json.loads(f.read())

df = pd.json_normalize(
data,
record_path =[‘students’],
meta=[
‘class’,
[‘info’, ‘president’],
[‘info’, ‘contacts’, ‘tel’]
]
)

print(df)
以上实例输出结果为：

 id   name  math  physics  chemistry   class info.president info.contacts.tel

0 A001 Tom 60 66 61 Year 1 John Kasich 123456789
1 A002 James 89 76 51 Year 1 John Kasich 123456789
2 A003 Jenny 79 90 78 Year 1 John Kasich 123456789

读取内嵌数据中的一组数据
以下是实例文件 nested_deep.json，我们只读取内嵌中的 math 字段：

nested_deep.json 文件内容
{
“school_name”: “local primary school”,
“class”: “Year 1”,
“students”: [
{
“id”: “A001”,
“name”: “Tom”,
“grade”: {
“math”: 60,
“physics”: 66,
“chemistry”: 61
}

},
{
    "id": "A002",
    "name": "James",
    "grade": {
        "math": 89,
        "physics": 76,
        "chemistry": 51
    }
   
},
{
    "id": "A003",
    "name": "Jenny",
    "grade": {
        "math": 79,
        "physics": 90,
        "chemistry": 78
    }
}]

}
这里我们需要使用到 glom 模块来处理数据套嵌，glom 模块允许我们使用 . 来访问内嵌对象的属性。

第一次使用我们需要安装 glom：

pip3 install glom
实例
import pandas as pd
from glom import glom

df = pd.read_json(‘nested_deep.json’)

data = df[‘students’].apply(lambda row: glom(row, ‘grade.math’))
print(data)
以上实例输出结果为：

0 60
1 89
2 79
Name: students, dtype: int64

2.6 数据清洗

数据清洗是对一些没有用的数据进行处理的过程。

很多数据集存在数据缺失、数据格式错误、错误数据或重复数据的情况，如果要对使数据分析更加准确，就需要对这些没有用的数据进行处理。

在这个教程中，我们将利用 Pandas包来进行数据清洗。
测试数据地址：https://static.runoob.com/download/property-data.csv

Pandas 清洗空值
如果我们要删除包含空字段的行，可以使用 dropna() 方法，语法格式如下：

DataFrame.dropna(axis=0, how=‘any’, thresh=None, subset=None, inplace=False)
参数说明：

axis：默认为 0，表示逢空值剔除整行，如果设置参数 axis＝1 表示逢空值去掉整列。
how：默认为 ‘any’ 如果一行（或一列）里任何一个数据有出现 NA 就去掉整行，如果设置 how=‘all’ 一行（或列）都是 NA 才去掉这整行。
thresh：设置需要多少非空值的数据才可以保留下来的。
subset：设置想要检查的列。如果是多个列，可以使用列名的 list 作为参数。
inplace：如果设置 True，将计算得到的值直接覆盖之前的值并返回 None，修改的是源数据。

我们可以通过 isnull() 判断各个单元格是否为空。
实例
import pandas as pd

df = pd.read_csv(‘property-data.csv’)

print (df[‘NUM_BEDROOMS’])
print (df[‘NUM_BEDROOMS’].isnull())
以上实例输出结果如下：

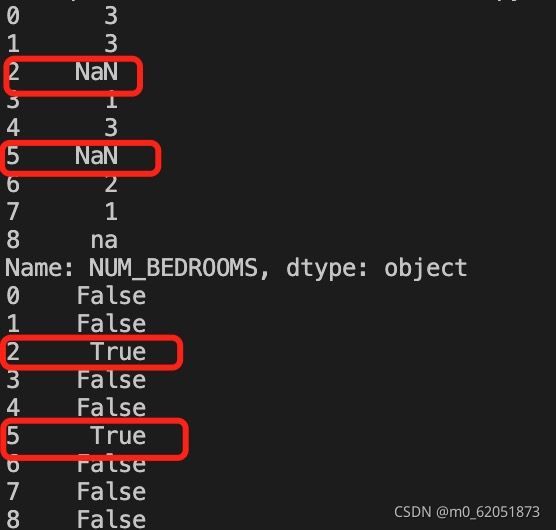
以上例子中我们看到 Pandas 把 n/a 和 NA 当作空数据，na 不是空数据，不符合我们要求，我们可以指定空数据类型：
import pandas as pd

missing_values = [“n/a”, “na”, “–”]
df = pd.read_csv(‘property-data.csv’, na_values = missing_values)

print (df[‘NUM_BEDROOMS’])
print (df[‘NUM_BEDROOMS’].isnull())
以上实例输出结果如下：

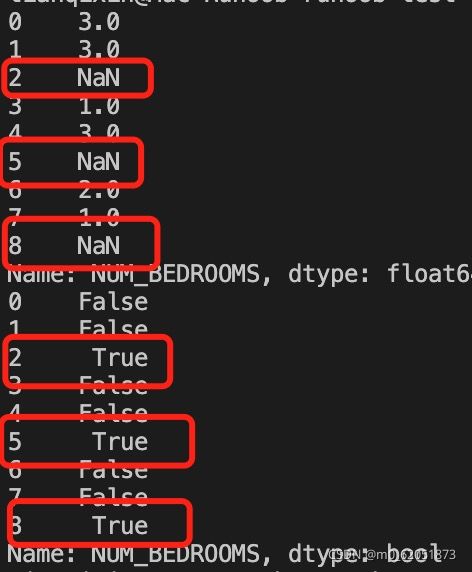
接下来的实例演示了删除包含空数据的行。
import pandas as pd

df = pd.read_csv(‘property-data.csv’)

new_df = df.dropna()

print(new_df.to_string())
以上实例输出结果如下：

注意：默认情况下，dropna() 方法返回一个新的 DataFrame，不会修改源数据。

如果你要修改源数据 DataFrame, 可以使用 inplace = True 参数:

我们也可以移除指定列有空值的行：

实例
移除 ST_NUM 列中字段值为空的行：

import pandas as pd

df = pd.read_csv(‘property-data.csv’)

df.dropna(subset=[‘ST_NUM’], inplace = True)

print(df.to_string())
以上实例输出结果如下：

我们也可以 fillna() 方法来替换一些空字段：
实例
使用 12345 替换空字段：
import pandas as pd

df = pd.read_csv(‘property-data.csv’)

df.fillna(12345, inplace = True)

print(df.to_string())
我们也可以指定某一个列来替换数据：
实例
使用 12345 替换 PID 为空数据：

import pandas as pd

df = pd.read_csv(‘property-data.csv’)

df[‘PID’].fillna(12345, inplace = True)

print(df.to_string())

替换空单元格的常用方法是计算列的均值、中位数值或众数。
Pandas使用 mean()、median() 和 mode() 方法计算列的均值（所有值加起来的平均值）、中位数值（排序后排在中间的数）和众数（出现频率最高的数）。
实例
使用 mean() 方法计算列的均值并替换空单元格：

import pandas as pd

df = pd.read_csv(‘property-data.csv’)

x = df[“ST_NUM”].mean()

df[“ST_NUM”].fillna(x, inplace = True)

print(df.to_string())

Pandas 清洗格式错误数据
数据格式错误的单元格会使数据分析变得困难，甚至不可能。

我们可以通过包含空单元格的行，或者将列中的所有单元格转换为相同格式的数据。

以下实例会格式化日期：
实例
import pandas as pd

第三个日期格式错误
data = {
“Date”: [‘2020/12/01’, ‘2020/12/02’ , ‘20201226’],
“duration”: [50, 40, 45]
}

df = pd.DataFrame(data, index = [“day1”, “day2”, “day3”])

df[‘Date’] = pd.to_datetime(df[‘Date’])

print(df.to_string())
Pandas 清洗错误数据
数据错误也是很常见的情况，我们可以对错误的数据进行替换或移除。

以下实例会替换错误年龄的数据：
实例
import pandas as pd

person = {
“name”: [‘Google’, ‘Runoob’ , ‘Taobao’],
“age”: [50, 40, 12345] # 12345 年龄数据是错误的
}

df = pd.DataFrame(person)
df.loc[2, ‘age’] = 30 # 修改数据

print(df.to_string())
也可以设置条件语句：
实例
将 age 大于 120 的设置为 120:

import pandas as pd

person = {
“name”: [‘Google’, ‘Runoob’ , ‘Taobao’],
“age”: [50, 200, 12345]
}

df = pd.DataFrame(person)

for x in df.index:
if df.loc[x, “age”] > 120:
df.loc[x, “age”] = 120

print(df.to_string())

也可以将错误数据的行删除：
实例
将 age 大于 120 的删除:

import pandas as pd

person = {
“name”: [‘Google’, ‘Runoob’ , ‘Taobao’],
“age”: [50, 40, 12345] # 12345 年龄数据是错误的
}

df = pd.DataFrame(person)

for x in df.index:
if df.loc[x, “age”] > 120:
df.drop(x, inplace = True)

print(df.to_string())

Pandas 清洗重复数据
如果我们要清洗重复数据，可以使用 duplicated() 和 drop_duplicates() 方法。

如果对应的数据是重复的，duplicated() 会返回 True，否则返回 False
import pandas as pd

person = {
“name”: [‘Google’, ‘Runoob’, ‘Runoob’, ‘Taobao’],
“age”: [50, 40, 40, 23]
}
df = pd.DataFrame(person)

print(df.duplicated())
以上实例输出结果如下：

0 False
1 False
2 True
3 False
dtype: bool
删除重复数据，可以直接使用drop_duplicates() 方法。

实例
import pandas as pd

persons = {
“name”: [‘Google’, ‘Runoob’, ‘Runoob’, ‘Taobao’],
“age”: [50, 40, 40, 23]
}

df = pd.DataFrame(persons)

df.drop_duplicates(inplace = True)
print(df)
以上实例输出结果如下：

 name  age

0 Google 50
1 Runoob 40
3 Taobao 23

3.matplotlib

3.1 matplotlib pyplot

import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([0, 6])
ypoints = np.array([0, 100])

plt.plot(xpoints, ypoints)
plt.show()
以上实例中我们使用了 Pyplot 的 plot() 函数， plot() 函数是绘制二维图形的最基本函数。

plot() 用于画图它可以绘制点和线，语法格式如下：

画单条线
plot([x], y, [fmt], *, data=None, **kwargs)
画多条线
plot([x], y, [fmt], [x2], y2, [fmt2], …, **kwargs)
参数说明：

x, y：点或线的节点，x 为 x 轴数据，y 为 y 轴数据，数据可以列表或数组。
fmt：可选，定义基本格式（如颜色、标记和线条样式）。
kwargs：可选，用在二维平面图上，设置指定属性，如标签，线的宽度等。
plot(x, y) # 创建 y 中数据与 x 中对应值的二维线图，使用默认样式
plot(x, y, ‘bo’) # 创建 y 中数据与 x 中对应值的二维线图，使用蓝色实心圈绘制
plot(y) # x 的值为 0…N-1
plot(y, ‘r+’) # 使用红色 + 号
颜色字符:‘b’ 蓝色，‘m’ 洋红色，‘g’ 绿色，‘y’ 黄色，‘r’ 红色，‘k’ 黑色，‘w’ 白色，‘c’ 青绿色，’#008000’ RGB 颜色符串。多条曲线不指定颜色时，会自动选择不同颜色。
线型参数：’‐’ 实线，’‐‐’ 破折线，’‐.’ 点划线，’:’ 虚线。
标记字符：’.’ 点标记，’,’ 像素标记(极小点)，‘o’ 实心圈标记，‘v’ 倒三角标记，’^’ 上三角标记，’>’ 右三角标记，’<’ 左三角标记…等等。

如果我们只想绘制两个坐标点，而不是一条线，可以使用 o 参数，表示一个实心圈的标记：

绘制坐标 (1, 3) 和 (8, 10) 的两个点
import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([1, 8])
ypoints = np.array([3, 10])

plt.plot(xpoints, ypoints, ‘o’)
plt.show()

我们也可以绘制任意数量的点，只需确保两个轴上的点数相同即可。

绘制一条不规则线，坐标为 (1, 3) 、 (2, 8) 、(6, 1) 、(8, 10)，对应的两个数组为：[1, 2, 6, 8] 与 [3, 8, 1, 10]。

实例
import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([1, 2, 6, 8])
ypoints = np.array([3, 8, 1, 10])

plt.plot(xpoints, ypoints)
plt.show()

如果我们不指定 x 轴上的点，则 x 会根据 y 的值来设置为 0, 1, 2, 3…N-1。

以下实例我们绘制一个正弦和余弦图，在 plt.plot() 参数中包含两对 x,y 值，第一对是 x,y，这对应于正弦函数，第二对是 x,z，这对应于余弦函数。

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0,4*np.pi,0.1)
# start,stop,step
y = np.sin(x)
z = np.cos(x)
plt.plot(x,y,x,z)
plt.show()

3.2Matplotlib 绘图标记

绘图过程如果我们想要给坐标自定义一些不一样的标记，就可以使用 plot() 方法的 marker 参数来定义。

以下实例定义了实心圆标记：
实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([1,3,4,5,8,9,6,1,3,4,5,2,4])

plt.plot(ypoints, marker = ‘o’)
plt.show()
显示结果如下：

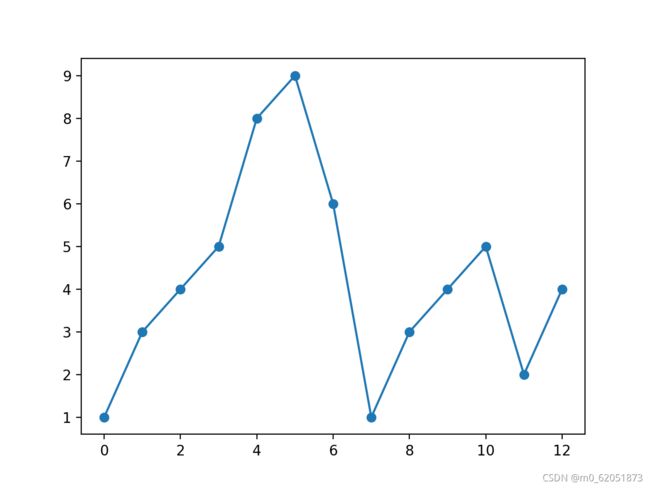
marker 可以定义的符号如下：
标记符号描述
“.” m00 点
“,” m01 像素点
“o” m02 实心圆
“v” m03 下三角
“^” m04 上三角
“<” m05 左三角
“>” m06 右三角
“1” m07 下三叉
“2” m08 上三叉
“3” m09 左三叉
“4” m10 右三叉
“8” m11 八角形
“s” m12 正方形
“p” m13 五边形
“P” m23 加号（填充）
“*” m14 星号
“h” m15 六边形 1
“H” m16 六边形 2
“+” m17 加号
“x” m18 乘号 x
“X” m24 乘号 x (填充)
“D” m19 菱形
“d” m20 瘦菱形
“|” m21 竖线
“_” m22 横线
0 (TICKLEFT) m25 左横线
1 (TICKRIGHT) m26 右横线
2 (TICKUP) m27 上竖线
3 (TICKDOWN) m28 下竖线
4 (CARETLEFT) m29 左箭头
5 (CARETRIGHT) m30 右箭头
6 (CARETUP) m31 上箭头
7 (CARETDOWN) m32 下箭头
8 (CARETLEFTBASE) m33 左箭头 (中间点为基准)
9 (CARETRIGHTBASE) m34 右箭头 (中间点为基准)
10 (CARETUPBASE) m35 上箭头 (中间点为基准)
11 (CARETDOWNBASE) m36 下箭头 (中间点为基准)
“None”, " " or “” 没有任何标记
‘ $. . .$ ’ m37 渲染指定的字符。例如 “ $f$ ” 以字母 f 为标记。
参考：https://www.runoob.com/matplotlib/matplotlib-marker.html

fmt 参数
fmt 参数定义了基本格式，如标记、线条样式和颜色。

fmt = ‘[marker][line][color]’
例如 o:r，o 表示实心圆标记，: 表示虚线，r 表示颜色为红色。

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, ‘o:r’)
plt.show()
线类型：

线类型标记描述
‘-’ 实线
‘:’ 虚线
‘–’ 破折线
‘-.’ 点划线

颜色类型：
颜色标记描述
‘r’ 红色
‘g’ 绿色
‘b’ 蓝色
‘c’ 青色
‘m’ 品红
‘y’ 黄色
‘k’ 黑色
‘w’ 白色

标记大小与颜色
我们可以自定义标记的大小与颜色，使用的参数分别是：
markersize，简写为 ms：定义标记的大小。
markerfacecolor，简写为 mfc：定义标记内部的颜色。
markeredgecolor，简写为 mec：定义标记边框的颜色
设置标记大小：

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, marker = ‘o’, ms = 20)
plt.show()
显示结果如下：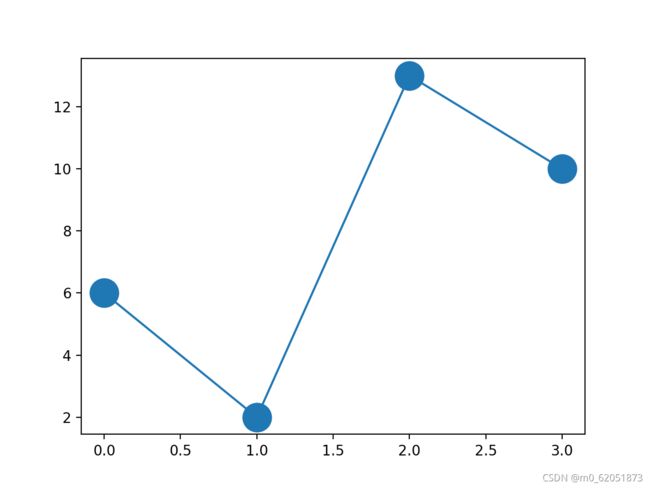

设置标记外边框颜色：
实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, marker = ‘o’, ms = 20, mec = ‘r’)
plt.show()
显示结果如下：

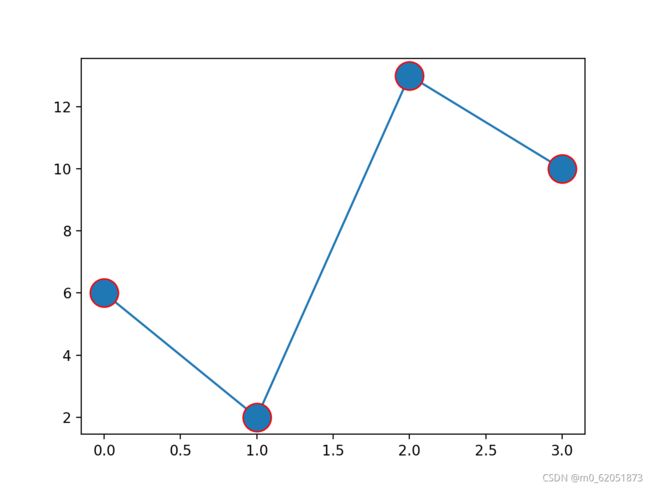
设置标记内部颜色：

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, marker = ‘o’, ms = 20, mfc = ‘r’)
plt.show()
显示结果如下：

3.3Matplotlib 绘图线

绘图过程如果我们自定义线的样式，包括线的类型、颜色和大小等。

线的类型
线的类型可以使用 linestyle 参数来定义，简写为 ls。
类型简写说明
‘solid’ (默认) ‘-’ 实线
‘dotted’ ‘:’ 点虚线
‘dashed’ ‘–’ 破折线
‘dashdot’ ‘-.’ 点划线
‘None’ ‘’ 或 ’ ’ 不画线

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, linestyle = ‘dotted’)
plt.show()

使用简写：

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, ls = ‘-.’)
plt.show()
线的颜色
线的颜色可以使用 color 参数来定义，简写为 c。

颜色类型：

颜色标记描述
‘r’ 红色
‘g’ 绿色
‘b’ 蓝色
‘c’ 青色
‘m’ 品红
‘y’ 黄色
‘k’ 黑色
‘w’ 白色
当然也可以自定义颜色类型，例如：SeaGreen、#8FBC8F 等，完整样式可以参考 HTML 颜色值。

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, color = ‘r’)
plt.show()

线的宽度
线的宽度可以使用 linewidth 参数来定义，简写为 lw，值可以是浮点数，如：1、2.0、5.67 等。

实例
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6, 2, 13, 10])

plt.plot(ypoints, linewidth = ‘12.5’)
plt.show()
多条线
plot() 方法中可以包含多对 x,y 值来绘制多条线。

实例
import matplotlib.pyplot as plt
import numpy as np

y1 = np.array([3, 7, 5, 9])
y2 = np.array([6, 2, 13, 10])

plt.plot(y1)
plt.plot(y2)

plt.show()
实例
import matplotlib.pyplot as plt
import numpy as np

x1 = np.array([0, 1, 2, 3])
y1 = np.array([3, 7, 5, 9])
x2 = np.array([0, 1, 2, 3])
y2 = np.array([6, 2, 13, 10])

plt.plot(x1, y1, x2, y2)
plt.show()

3.4Matplotlib 轴标签和标题

我们可以使用 xlabel() 和 ylabel() 方法来设置 x 轴和 y 轴的标签。
import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3, 4])
y = np.array([1, 4, 9, 16])
plt.plot(x, y)

plt.xlabel(“x - label”)
plt.ylabel(“y - label”)

plt.show()

标题
我们可以使用 title() 方法来设置标题。

实例
import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3, 4])
y = np.array([1, 4, 9, 16])
plt.plot(x, y)

plt.title(“RUNOOB TEST TITLE”)
plt.xlabel(“x - label”)
plt.ylabel(“y - label”)

plt.show()

3.5 Matplotlib 网格线

我们可以使用 pyplot 中的 grid() 方法来设置图表中的网格线。

grid() 方法语法格式如下：

matplotlib.pyplot.grid(b=None, which=‘major’, axis=‘both’, )
参数说明：

b：可选，默认为 None，可以设置布尔值，true 为显示网格线，false 为不显示，如果设置 **kwargs 参数，则值为 true。
which：可选，可选值有 ‘major’、‘minor’ 和 ‘both’，默认为 ‘major’，表示应用更改的网格线。
axis：可选，设置显示哪个方向的网格线，可以是取 ‘both’（默认），‘x’ 或 ‘y’，分别表示两个方向，x 轴方向或 y 轴方向。
**kwargs：可选，设置网格样式，可以是 color=‘r’, linestyle=’-’ 和 linewidth=2，分别表示网格线的颜色，样式和宽度。
plt.grid()
以下实例添加一个简单的网格线，axis 参数使用 x，设置 x 轴方向显示网格线：

实例
import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3, 4])
y = np.array([1, 4, 9, 16])

plt.title(“RUNOOB grid() Test”)
plt.xlabel(“x - label”)
plt.ylabel(“y - label”)

plt.plot(x, y)

plt.grid(axis=‘x’) # 设置 y 就在轴方向显示网格线

plt.show()

以下实例添加一个简单的网格线，并设置网格线的样式，格式如下：

grid(color = ‘color’, linestyle = ‘linestyle’, linewidth = number)
参数说明：

color：‘b’ 蓝色，‘m’ 洋红色，‘g’ 绿色，‘y’ 黄色，‘r’ 红色，‘k’ 黑色，‘w’ 白色，‘c’ 青绿色，’#008000’ RGB 颜色符串。

linestyle：’‐’ 实线，’‐‐’ 破折线，’‐.’ 点划线，’:’ 虚线。

linewidth：设置线的宽度，可以设置一个数字。

实例
import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3, 4])
y = np.array([1, 4, 9, 16])

plt.title(“RUNOOB grid() Test”)
plt.xlabel(“x - label”)
plt.ylabel(“y - label”)

plt.plot(x, y)

plt.grid(color = ‘r’, linestyle = ‘–’, linewidth = 0.5)

plt.show()

3.6Matplotlib 绘制多图

我们可以使用 pyplot 中的 subplot() 和 subplots() 方法来绘制多个子图。

subpot() 方法在绘图时需要指定位置，subplots() 方法可以一次生成多个，在调用时只需要调用生成对象的 ax 即可。
subplot
subplot(nrows, ncols, index, **kwargs)
subplot(pos, **kwargs)
subplot(**kwargs)
subplot(ax)
以上函数将整个绘图区域分成 nrows 行和 ncols 列，然后从左到右，从上到下的顺序对每个子区域进行编号 1…N ，左上的子区域的编号为 1、右下的区域编号为 N，编号可以通过参数 index 来设置。

设置 numRows ＝ 1，numCols ＝ 2，就是将图表绘制成 1x2 的图片区域, 对应的坐标为：

(1, 1), (1, 2)
plotNum ＝ 1, 表示的坐标为(1, 1), 即第一行第一列的子图。

plotNum ＝ 2, 表示的坐标为(1, 2), 即第一行第二列的子图。
实例
import matplotlib.pyplot as plt
import numpy as np

#plot 1:
xpoints = np.array([0, 6])
ypoints = np.array([0, 100])

plt.subplot(1, 2, 1)
plt.plot(xpoints,ypoints)
plt.title(“plot 1”)

#plot 2:
x = np.array([1, 2, 3, 4])
y = np.array([1, 4, 9, 16])

plt.subplot(1, 2, 2)
plt.plot(x,y)
plt.title(“plot 2”)

plt.suptitle(“RUNOOB subplot Test”)
plt.show()

设置 numRows ＝ 2，numCols ＝ 2，就是将图表绘制成 2x2 的图片区域, 对应的坐标为：

(1, 1), (1, 2)
(2, 1), (2, 2)
plotNum ＝ 1, 表示的坐标为(1, 1), 即第一行第一列的子图。

plotNum ＝ 2, 表示的坐标为(1, 2), 即第一行第二列的子图。

plotNum ＝ 3, 表示的坐标为(2, 1), 即第二行第一列的子图。

plotNum ＝ 4, 表示的坐标为(2, 2), 即第二行第二列的子图。

实例
import matplotlib.pyplot as plt
import numpy as np

#plot 1:
x = np.array([0, 6])
y = np.array([0, 100])

plt.subplot(2, 2, 1)
plt.plot(x,y)
plt.title(“plot 1”)

#plot 2:
x = np.array([1, 2, 3, 4])
y = np.array([1, 4, 9, 16])

plt.subplot(2, 2, 2)
plt.plot(x,y)
plt.title(“plot 2”)

#plot 3:
x = np.array([1, 2, 3, 4])
y = np.array([3, 5, 7, 9])

plt.subplot(2, 2, 3)
plt.plot(x,y)
plt.title(“plot 3”)

#plot 4:
x = np.array([1, 2, 3, 4])
y = np.array([4, 5, 6, 7])

plt.subplot(2, 2, 4)
plt.plot(x,y)
plt.title(“plot 4”)

plt.suptitle(“RUNOOB subplot Test”)
plt.show()

subplots()
subplots() 方法语法格式如下：

matplotlib.pyplot.subplots(nrows=1, ncols=1, , sharex=False, sharey=False, squeeze=True, subplot_kw=None, gridspec_kw=None, **fig_kw)
参数说明：
nrows：默认为 1，设置图表的行数。
ncols：默认为 1，设置图表的列数。
sharex、sharey：设置 x、y 轴是否共享属性，默认为 false，可设置为 ‘none’、‘all’、‘row’ 或 ‘col’。 False 或 none 每个子图的 x 轴或 y 轴都是独立的，True 或 ‘all’：所有子图共享 x 轴或 y 轴，‘row’ 设置每个子图行共享一个 x 轴或 y 轴，‘col’：设置每个子图列共享一个 x 轴或 y 轴。
squeeze：布尔值，默认为 True，表示额外的维度从返回的 Axes(轴)对象中挤出，对于 N1 或 1N 个子图，返回一个 1 维数组，对于 NM，N>1 和 M>1 返回一个 2 维数组。如果设置为 False，则不进行挤压操作，返回一个元素为 Axes 实例的2维数组，即使它最终是1x1。
subplot_kw：可选，字典类型。把字典的关键字传递给 add_subplot() 来创建每个子图。
gridspec_kw：可选，字典类型。把字典的关键字传递给 GridSpec 构造函数创建子图放在网格里(grid)。
**fig_kw：把详细的关键字参数传给 figure() 函数。
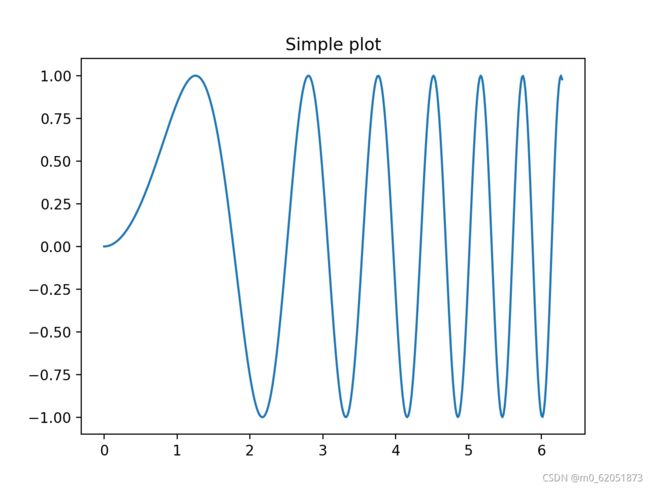
import matplotlib.pyplot as plt
import numpy as np

#创建一些测试数据 – 图1
x = np.linspace(0, 2*np.pi, 400)
y = np.sin(x**2)

#创建一个画像和子图 – 图2
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_title(‘Simple plot’)

#创建两个子图 – 图3
f, (ax1, ax2) = plt.subplots(1, 2, sharey=True)
ax1.plot(x, y)
ax1.set_title(‘Sharing Y axis’)
ax2.scatter(x, y)

#创建四个子图 – 图4
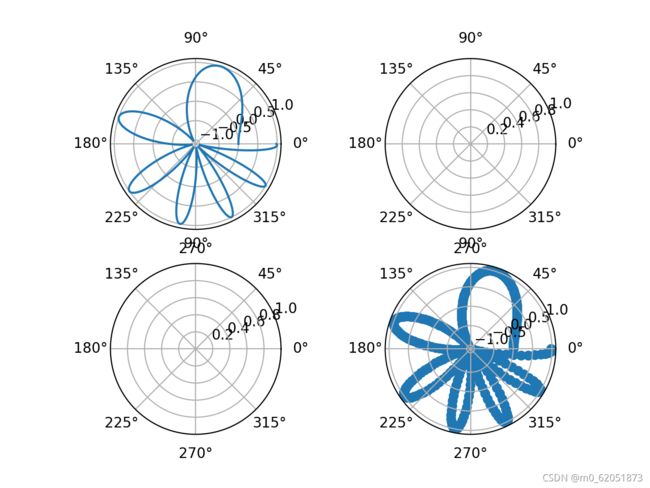
fig, axs = plt.subplots(2, 2, subplot_kw=dict(projection=“polar”))
axs[0, 0].plot(x, y)
axs[1, 1].scatter(x, y)

#共享 x 轴
plt.subplots(2, 2, sharex=‘col’)

#共享 y 轴
plt.subplots(2, 2, sharey=‘row’)

#共享 x 轴和 y 轴
plt.subplots(2, 2, sharex=‘all’, sharey=‘all’)

#这个也是共享 x 轴和 y 轴
plt.subplots(2, 2, sharex=True, sharey=True)

#创建10 张图，已经存在的则删除
fig, ax = plt.subplots(num=10, clear=True)

plt.show()
部分图表显示结果如下：

3.7 matplotlib 散点图

我们可以使用 pyplot 中的 scatter() 方法来绘制散点图。
scatter() 方法语法格式如下：

matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, *, edgecolors=None, plotnonfinite=False, data=None, **kwargs)
参数说明：

x，y：长度相同的数组，也就是我们即将绘制散点图的数据点，输入数据。

s：点的大小，默认 20，也可以是个数组，数组每个参数为对应点的大小。

c：点的颜色，默认蓝色 ‘b’，也可以是个 RGB 或 RGBA 二维行数组。

marker：点的样式，默认小圆圈 ‘o’。

cmap：Colormap，默认 None，标量或者是一个 colormap 的名字，只有 c 是一个浮点数数组的时才使用。如果没有申明就是 image.cmap。

norm：Normalize，默认 None，数据亮度在 0-1 之间，只有 c 是一个浮点数的数组的时才使用。

vmin，vmax：：亮度设置，在 norm 参数存在时会忽略。

alpha：：透明度设置，0-1 之间，默认 None，即不透明。

linewidths：：标记点的长度。

edgecolors：：颜色或颜色序列，默认为 ‘face’，可选值有 ‘face’, ‘none’, None。

plotnonfinite：：布尔值，设置是否使用非限定的 c ( inf, -inf 或 nan) 绘制点。

**kwargs：：其他参数。

以下实例 scatter() 函数接收长度相同的数组参数，一个用于 x 轴的值，另一个用于 y 轴上的值：
实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = np.array([1, 4, 9, 16, 7, 11, 23, 18])

plt.scatter(x, y)
plt.show()
显示结果如下：

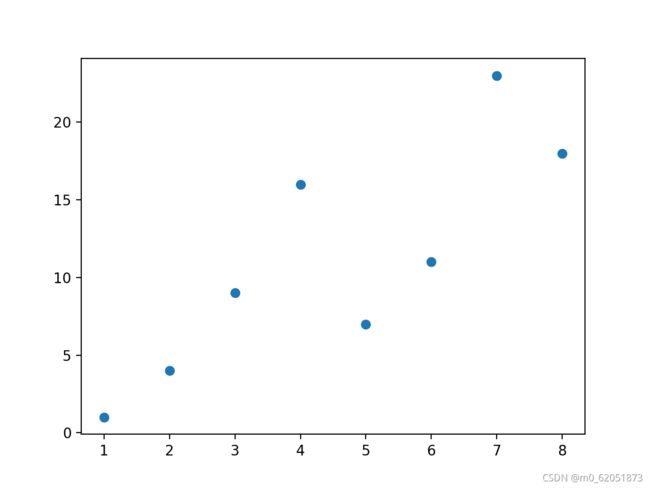
设置图标大小：

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = np.array([1, 4, 9, 16, 7, 11, 23, 18])
sizes = np.array([20,50,100,200,500,1000,60,90])
plt.scatter(x, y, s=sizes)
plt.show()
显示结果如下：

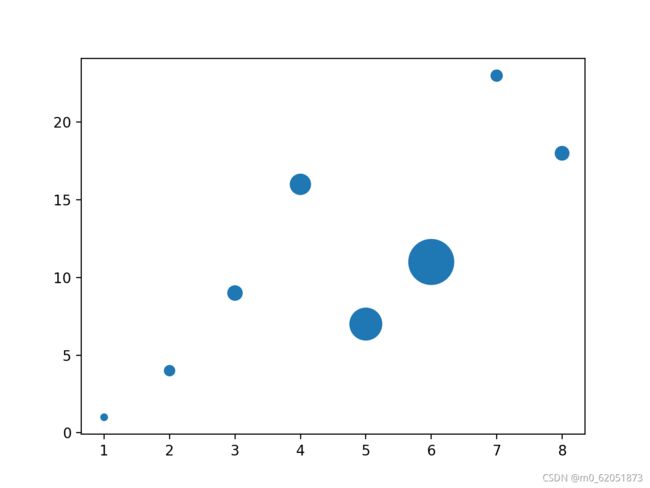
自定义点的颜色：

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = np.array([1, 4, 9, 16, 7, 11, 23, 18])
colors = np.array([“red”,“green”,“black”,“orange”,“purple”,“beige”,“cyan”,“magenta”])

plt.scatter(x, y, c=colors)
plt.show()
显示结果如下：

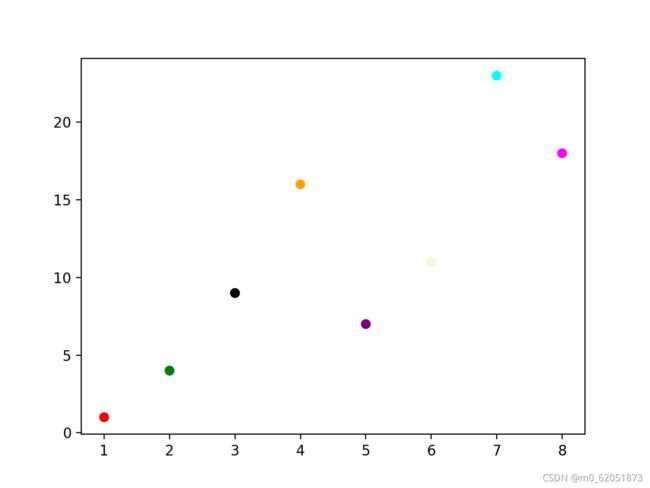
设置两组散点图：

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
plt.scatter(x, y, color = ‘hotpink’)

x = np.array([2,2,8,1,15,8,12,9,7,3,11,4,7,14,12])
y = np.array([100,105,84,105,90,99,90,95,94,100,79,112,91,80,85])
plt.scatter(x, y, color = ‘#88c999’)

plt.show()
显示结果如下：

使用随机数来设置散点图：

实例
import numpy as np
import matplotlib.pyplot as plt

#随机数生成器的种子
np.random.seed(19680801)

N = 50
x = np.random.rand(N)
y = np.random.rand(N)
colors = np.random.rand(N)
area = (30 * np.random.rand(N))**2 # 0 to 15 point radii #设置大小

plt.scatter(x, y, s=area, c=colors, alpha=0.5) # 设置颜色及透明度

plt.title(“RUNOOB Scatter Test”) # 设置标题

plt.show()

显示结果如下：

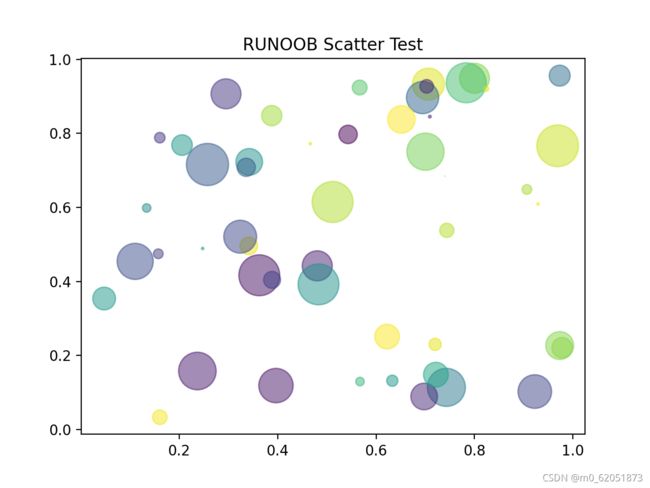
颜色条 Colormap
Matplotlib 模块提供了很多可用的颜色条。

颜色条就像一个颜色列表，其中每种颜色都有一个范围从 0 到 100 的值。

下面是一个颜色条的例子：

设置颜色条需要使用 cmap 参数，默认值为 ‘viridis’，之后颜色值设置为 0 到 100 的数组。
实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
colors = np.array([0, 10, 20, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100])

plt.scatter(x, y, c=colors, cmap=‘viridis’)

plt.show()
显示结果如下：
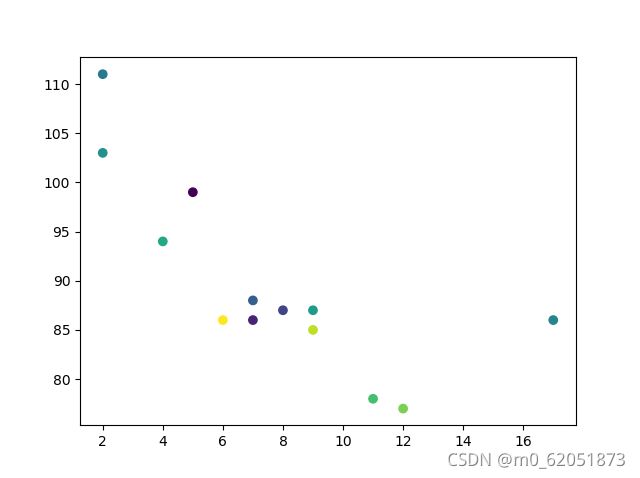如果要显示颜色条，需要使用 plt.colorbar() 方法：
import matplotlib.pyplot as plt
import numpy as np

x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
colors = np.array([0, 10, 20, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100])

plt.scatter(x, y, c=colors, cmap=‘viridis’)

plt.colorbar()

plt.show()
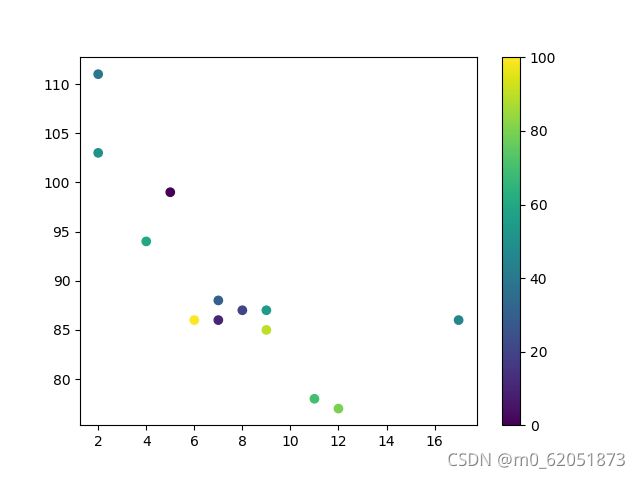换个颜色条参数， cmap 设置为 afmhot_r：
import matplotlib.pyplot as plt
import numpy as np

x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
colors = np.array([0, 10, 20, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100])

plt.scatter(x, y, c=colors, cmap=‘afmhot_r’)
plt.colorbar()
plt.show()

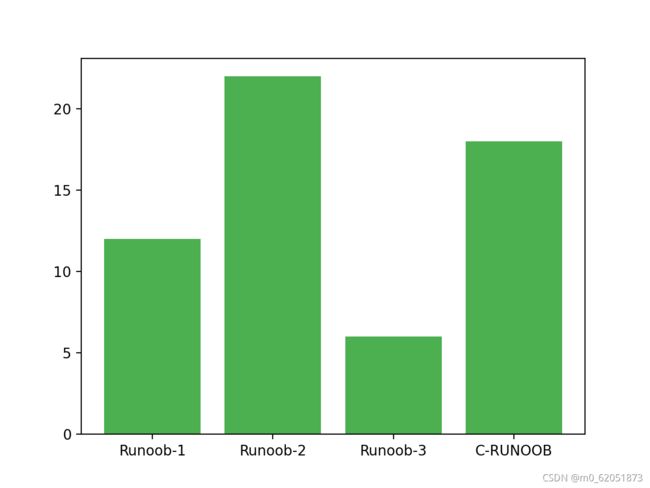
3.8 matplotlib 柱形图

我们可以使用 pyplot 中的 bar() 方法来绘制柱形图。
bar() 方法语法格式如下：

matplotlib.pyplot.bar(x, height, width=0.8, bottom=None, *, align=‘center’, data=None, **kwargs)
参数说明：

x：浮点型数组，柱形图的 x 轴数据。

height：浮点型数组，柱形图的高度。

width：浮点型数组，柱形图的宽度。

bottom：浮点型数组，底座的 y 坐标，默认 0。

align：柱形图与 x 坐标的对齐方式，‘center’ 以 x 位置为中心，这是默认值。 ‘edge’：将柱形图的左边缘与 x 位置对齐。要对齐右边缘的条形，可以传递负数的宽度值及 align=‘edge’。

**kwargs：：其他参数。

以下实例我们简单实用 bar() 来创建一个柱形图:
import matplotlib.pyplot as plt
import numpy as np

x = np.array([“Runoob-1”, “Runoob-2”, “Runoob-3”, “C-RUNOOB”])
y = np.array([12, 22, 6, 18])

plt.bar(x,y)
plt.show()

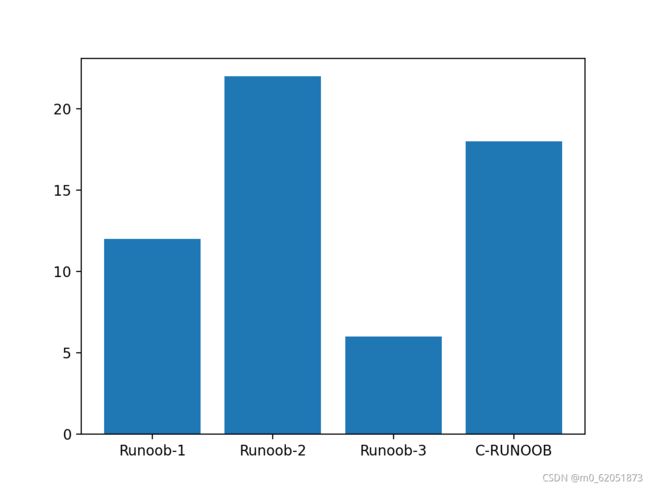
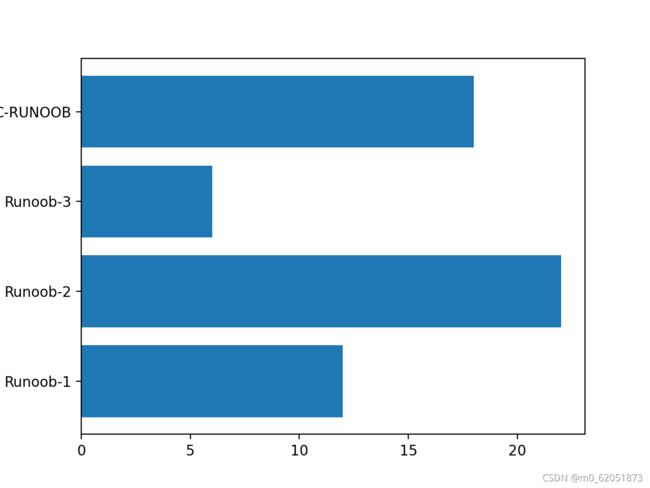
垂直方向的柱形图可以使用 barh() 方法来设置：

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([“Runoob-1”, “Runoob-2”, “Runoob-3”, “C-RUNOOB”])
y = np.array([12, 22, 6, 18])

plt.barh(x,y)
plt.show()

设置柱形图颜色：

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([“Runoob-1”, “Runoob-2”, “Runoob-3”, “C-RUNOOB”])
y = np.array([12, 22, 6, 18])

plt.bar(x, y, color = “#4CAF50”)
plt.show()

自定义各个柱形的颜色：

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([“Runoob-1”, “Runoob-2”, “Runoob-3”, “C-RUNOOB”])
y = np.array([12, 22, 6, 18])

plt.bar(x, y, color = ["#4CAF50",“red”,“hotpink”,"#556B2F"])
plt.show()

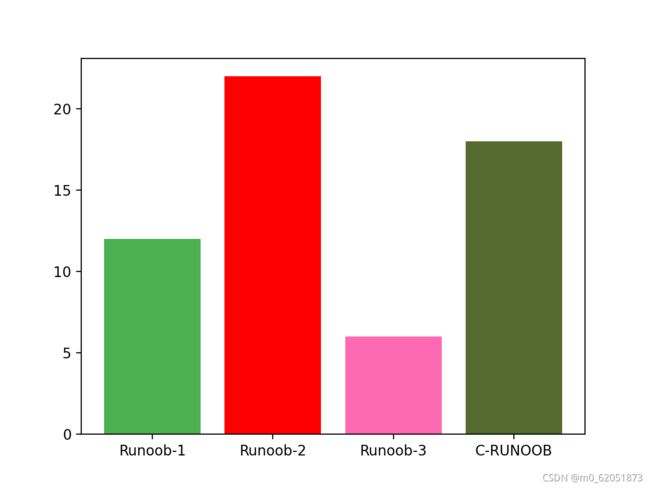
设置柱形图宽度，bar() 方法使用 width 设置，barh() 方法使用 height 设置 height

实例
import matplotlib.pyplot as plt
import numpy as np

x = np.array([“Runoob-1”, “Runoob-2”, “Runoob-3”, “C-RUNOOB”])
y = np.array([12, 22, 6, 18])

plt.bar(x, y, width = 0.1)
plt.show()

3.8 matplotlib 饼图

我们可以使用 pyplot 中的 pie() 方法来绘制饼图。

pie() 方法语法格式如下：
matplotlib.pyplot.pie(x, explode=None, labels=None, colors=None, autopct=None, pctdistance=0.6, shadow=False, labeldistance=1.1, startangle=0, radius=1, counterclock=True, wedgeprops=None, textprops=None, center=0, 0, frame=False, rotatelabels=False, *, normalize=None, data=None)[source]
参数说明：

x：浮点型数组，表示每个扇形的面积。

explode：数组，表示各个扇形之间的间隔，默认值为0。

labels：列表，各个扇形的标签，默认值为 None。

colors：数组，表示各个扇形的颜色，默认值为 None。

autopct：设置饼图内各个扇形百分比显示格式，%d%% 整数百分比，%0.1f 一位小数， %0.1f%% 一位小数百分比， %0.2f%% 两位小数百分比。

labeldistance：标签标记的绘制位置，相对于半径的比例，默认值为 1.1，如 <1则绘制在饼图内侧。

pctdistance：：类似于 labeldistance，指定 autopct 的位置刻度，默认值为 0.6。

shadow：：布尔值 True 或 False，设置饼图的阴影，默认为 False，不设置阴影。

radius：：设置饼图的半径，默认为 1。

startangle：：起始绘制饼图的角度，默认为从 x 轴正方向逆时针画起，如设定 =90 则从 y 轴正方向画起。

counterclock：布尔值，设置指针方向，默认为 True，即逆时针，False 为顺时针。

wedgeprops ：字典类型，默认值 None。参数字典传递给 wedge 对象用来画一个饼图。例如：wedgeprops={‘linewidth’:5} 设置 wedge 线宽为5。

textprops ：字典类型，默认值为：None。传递给 text 对象的字典参数，用于设置标签（labels）和比例文字的格式。

center ：浮点类型的列表，默认值：(0,0)。用于设置图标中心位置。

frame ：布尔类型，默认值：False。如果是 True，绘制带有表的轴框架。

rotatelabels ：布尔类型，默认为 False。如果为 True，旋转每个 label 到指定的角度。

以下实例我们简单实用 pie() 来创建一个柱形图:
mport matplotlib.pyplot as plt
import numpy as np

y = np.array([35, 25, 25, 15])

plt.pie(y)
plt.show()

设置饼图各个扇形的标签与颜色：

实例
import matplotlib.pyplot as plt
import numpy as np

y = np.array([35, 25, 25, 15])

plt.pie(y,
labels=[‘A’,‘B’,‘C’,‘D’], # 设置饼图标签
colors=["#d5695d", “#5d8ca8”, “#65a479”, “#a564c9”], # 设置饼图颜色
)
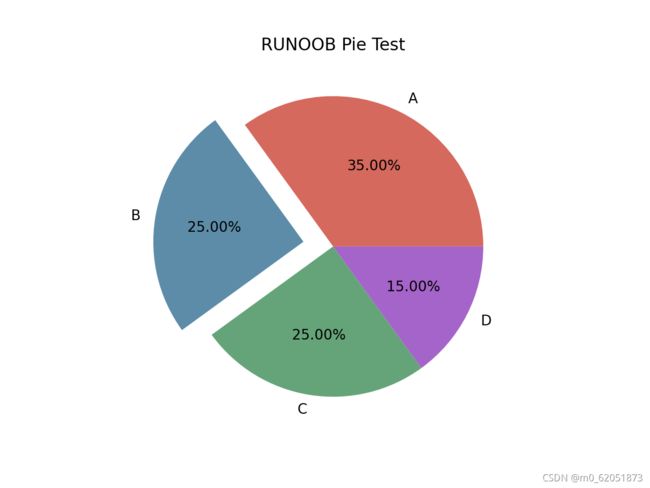
plt.title(“RUNOOB Pie Test”) # 设置标题
plt.show()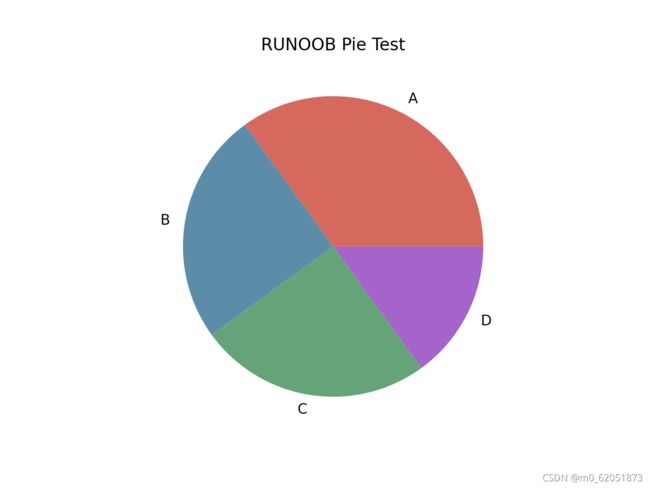

实例
import matplotlib.pyplot as plt
import numpy as np

y = np.array([35, 25, 25, 15])

plt.pie(y,
labels=[‘A’,‘B’,‘C’,‘D’], # 设置饼图标签
colors=["#d5695d", “#5d8ca8”, “#65a479”, “#a564c9”], # 设置饼图颜色
explode=(0, 0.2, 0, 0), # 第二部分突出显示，值越大，距离中心越远
autopct=’%.2f%%’, # 格式化输出百分比
)
plt.title(“RUNOOB Pie Test”)
plt.show()

4.scipy

SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。
SciPy 应用
Scipy 是一个用于数学、科学、工程领域的常用软件包，可以处理最优化、线性代数、积分、插值、拟合、特殊函数、快速傅里叶变换、信号处理、图像处理、常微分方程求解器等。。

SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。

NumPy 和 SciPy 的协同工作可以高效解决很多问题，在天文学、生物学、气象学和气候科学，以及材料科学等多个学科得到了广泛应用。
SciPy 模块列表
以下列出了 SciPy 常用的一些模块及官网 API 地址：
模块名功能参考文档
scipy.cluster 向量量化 cluster API
scipy.constants 数学常量 constants API
scipy.fft 快速傅里叶变换 fft API
scipy.integrate 积分 integrate API
scipy.interpolate 插值 interpolate API
scipy.io 数据输入输出 io API
scipy.linalg 线性代数 linalg API
scipy.misc 图像处理 misc API
scipy.ndimage N 维图像 ndimage API
scipy.odr 正交距离回归 odr API
scipy.optimize 优化算法 optimize API
scipy.signal 信号处理 signal API
scipy.sparse 稀疏矩阵 sparse API
scipy.spatial 空间数据结构和算法 spatial API
scipy.special 特殊数学函数 special API
scipy/stats 统计函数 stats.mstats API

4.1 scipy 优化器

最小值，方程解问题
SciPy 的 optimize 模块提供了常用的最优化算法函数实现，我们可以直接调用这些函数完成我们的优化问题，比如查找函数的最小值或方程的根等。

NumPy 能够找到多项式和线性方程的根，但它无法找到非线性方程的根
root(fun,x0) fun 表示方程的函数，x0表示根的初始猜测

实例
查找 x + cos(x) 方程的根:

from scipy.optimize import root
from math import cos
def eqn(x):
return x + cos(x)

myroot = root(eqn, 0)

print(myroot.x)
#查看更多信息
#print(myroot)

最小化函数

函数表示一条曲线，曲线有高点和低点。

高点称为最大值。

低点称为最小值。

整条曲线中的最高点称为全局最大值，其余部分称为局部最大值。

整条曲线的最低点称为全局最小值，其余的称为局部最小值。

可以使用 scipy.optimize.minimize() 函数来最小化函数。
minimize() 函接受以下几个参数：

fun - 要优化的函数
x0 - 初始猜测值
method - 要使用的方法名称，值可以是：‘CG’，‘BFGS’，‘Newton-CG’，‘L-BFGS-B’，‘TNC’，‘COBYLA’，，‘SLSQP’。
callback - 每次优化迭代后调用的函数。
options - 定义其他参数的字典：
实例
x^2 + x + 2 使用 BFGS 的最小化函数:

from scipy.optimize import minimize

def eqn(x):
return x**2 + x + 2

mymin = minimize(eqn, 0, method=‘BFGS’)

print(mymin)

4.2 SciPy 稀疏矩阵

稀疏矩阵（英语：sparse matrix）指的是在数值分析中绝大多数数值为零的矩阵。反之，如果大部分元素都非零，则这个矩阵是稠密的(Dense)。

在科学与工程领域中求解线性模型时经常出现大型的稀疏矩阵。
看一个简单例子：

上述稀疏矩阵仅包含 9 个非零元素，另外包含 26 个零元。其稀疏度为 74%，密度为 26%。

SciPy 的 scipy.sparse 模块提供了处理稀疏矩阵的函数。

我们主要使用以下两种类型的稀疏矩阵：

CSC - 压缩稀疏列（Compressed Sparse Column），按列压缩。
CSR - 压缩稀疏行（Compressed Sparse Row），按行压缩。
本章节我们主要使用 CSR 矩阵。
CSR 矩阵
我们可以通过向 scipy.sparse.csr_matrix() 函数传递数组来创建一个 CSR 矩阵。

实例
创建 CSR 矩阵。

import numpy as np
from scipy.sparse import csr_matrix

arr = np.array([0, 0, 0, 0, 0, 1, 1, 0, 2])

print(csr_matrix(arr))
以上代码输出结果为：

(0, 5) 1
(0, 6) 1
(0, 8) 2
结果解析：

第一行：在矩阵第一行（索引值 0 ）第六（索引值 5 ）个位置有一个数值 1。
第二行：在矩阵第一行（索引值 0 ）第七（索引值 6 ）个位置有一个数值 1。
第三行：在矩阵第一行（索引值 0 ）第九（索引值 8 ）个位置有一个数值 2。
CSR 矩阵方法
我们可以使用 data 属性查看存储的数据（不含 0 元素）：

实例
import numpy as np
from scipy.sparse import csr_matrix

arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])

print(csr_matrix(arr).data)
以上代码输出结果为：

[1 1 2]

使用 count_nonzero() 方法计算非 0 元素的总数：

实例
import numpy as np
from scipy.sparse import csr_matrix

arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])

print(csr_matrix(arr).count_nonzero())
以上代码输出结果为：

使用 remove_zeros() 方法删除矩阵中 0 元素：

实例
import numpy as np
from scipy.sparse import csr_matrix

arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])

mat = csr_matrix(arr)
mat.eliminate_zeros()

print(mat)
使用 sum_duplicates() 方法来删除重复项:

实例
import numpy as np
from scipy.sparse import csr_matrix

arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])

mat = csr_matrix(arr)
mat.sum_duplicates()

print(mat)
以上代码输出结果为：

(1, 2) 1
(2, 0) 1
(2, 2) 2

csr 转换为 csc 使用 tocsc() 方法：

实例
import numpy as np
from scipy.sparse import csr_matrix

arr = np.array([[0, 0, 0], [0, 0, 1], [1, 0, 2]])

newarr = csr_matrix(arr).tocsc()

print(newarr)
(2, 0) 1
(1, 2) 1
(2, 2) 2

4.3 scipy图结构

图结构是算法学中最强大的框架之一。

图是各种关系的节点和边的集合，节点是与对象对应的顶点，边是对象之间的连接。

SciPy 提供了 scipy.sparse.csgraph 模块来处理图结构。
连接组件
查看所有连接组件使用 connected_components() 方法。

实例
import numpy as np
from scipy.sparse.csgraph import connected_components
from scipy.sparse import csr_matrix

arr = np.array([
[0, 1, 2],
[1, 0, 0],
[2, 0, 0]
])

newarr = csr_matrix(arr)

print(connected_components(newarr))
以上代码输出结果为：

(1, array([0, 0, 0], dtype=int32))

Dijkstra – 最短路径算法
Dijkstra(迪杰斯特拉)最短路径算法，用于计算一个节点到其他所有节点的最短路径。

Scipy 使用 dijkstra() 方法来计算一个元素到其他元素的最短路径。

dijkstra() 方法可以设置以下几个参数：
return_predecessors: 布尔值，设置 True，遍历所有路径，如果不想遍历所有路径可以设置为 False。
indices: 元素的索引，返回该元素的所有路径。
limit: 路径的最大权重。

实例
查找元素 1 到 2 的最短路径：

import numpy as np
from scipy.sparse.csgraph import dijkstra
from scipy.sparse import csr_matrix

arr = np.array([
[0, 1, 2],
[1, 0, 0],
[2, 0, 0]
])

newarr = csr_matrix(arr)

print(dijkstra(newarr, return_predecessors=True, indices=0))
以上代码输出结果为：

(array([ 0., 1., 2.]), array([-9999, 0, 0], dtype=int32))

Floyd Warshall – 弗洛伊德算法
弗洛伊德算法算法是解决任意两点间的最短路径的一种算法。

Scipy 使用 floyd_warshall() 方法来查找所有元素对之间的最短路径。

实例
查找所有元素对之间的最短路径径：

import numpy as np
from scipy.sparse.csgraph import floyd_warshall
from scipy.sparse import csr_matrix

arr = np.array([
[0, 1, 2],
[1, 0, 0],
[2, 0, 0]
])

newarr = csr_matrix(arr)

print(floyd_warshall(newarr, return_predecessors=True))
以上代码输出结果为：

(array([[ 0., 1., 2.],
[ 1., 0., 3.],
[ 2., 3., 0.]]), array([[-9999, 0, 0],
[ 1, -9999, 0],
[ 2, 0, -9999]], dtype=int32))
Bellman Ford – 贝尔曼-福特算法
贝尔曼-福特算法是解决任意两点间的最短路径的一种算法。

Scipy 使用 bellman_ford() 方法来查找所有元素对之间的最短路径，通常可以在任何图中使用，包括有向图、带负权边的图。
实例
使用负权边的图查找从元素 1 到元素 2 的最短路径：

import numpy as np
from scipy.sparse.csgraph import bellman_ford
from scipy.sparse import csr_matrix

arr = np.array([
[0, -1, 2],
[1, 0, 0],
[2, 0, 0]
])

newarr = csr_matrix(arr)

print(bellman_ford(newarr, return_predecessors=True, indices=0))
以上代码输出结果为：

(array([ 0., -1., 2.]), array([-9999, 0, 0], dtype=int32))
深度优先顺序
depth_first_order() 方法从一个节点返回深度优先遍历的顺序。

可以接收以下参数：

图
图开始遍历的元素
实例
给定一个邻接矩阵，返回深度优先遍历的顺序：

import numpy as np
from scipy.sparse.csgraph import depth_first_order
from scipy.sparse import csr_matrix

arr = np.array([
[0, 1, 0, 1],
[1, 1, 1, 1],
[2, 1, 1, 0],
[0, 1, 0, 1]
])

newarr = csr_matrix(arr)

print(depth_first_order(newarr, 1))
以上代码输出结果为：

(array([1, 0, 3, 2], dtype=int32), array([ 1, -9999, 1, 0], dtype=int32))
广度优先顺序
breadth_first_order() 方法从一个节点返回广度优先遍历的顺序。

可以接收以下参数：

图
图开始遍历的元素
实例
给定一个邻接矩阵，返回广度优先遍历的顺序：

import numpy as np
from scipy.sparse.csgraph import breadth_first_order
from scipy.sparse import csr_matrix

arr = np.array([
[0, 1, 0, 1],
[1, 1, 1, 1],
[2, 1, 1, 0],
[0, 1, 0, 1]
])

newarr = csr_matrix(arr)

print(breadth_first_order(newarr, 1))
以上代码输出结果为：

(array([1, 0, 2, 3], dtype=int32), array([ 1, -9999, 1, 1], dtype=int32))

4.4scipy空间数据

间数据又称几何数据，它用来表示物体的位置、形态、大小分布等各方面的信息，比如坐标上的点。

SciPy 通过 scipy.spatial 模块处理空间数据，比如判断一个点是否在边界内、计算给定点周围距离最近点以及给定距离内的所有点。
三角测量
三角测量在三角学与几何学上是一借由测量目标点与固定基准线的已知端点的角度，测量目标距离的方法。

多边形的三角测量是将多边形分成多个三角形，我们可以用这些三角形来计算多边形的面积。

拓扑学的一个已知事实告诉我们：任何曲面都存在三角剖分。

假设曲面上有一个三角剖分，我们把所有三角形的顶点总个数记为 p(公共顶点只看成一个)，边数记为 a，三角形的个数记为 n，则 e=p-a+n 是曲面的拓扑不变量。也就是说不管是什么剖分，e 总是得到相同的数值。 e 被称为称为欧拉示性数。

对一系列的点进行三角剖分点方法是 Delaunay() 三角剖分。
import numpy as np
from scipy.spatial import Delaunay
import matplotlib.pyplot as plt

points = np.array([
[2, 4],
[3, 4],
[3, 0],
[2, 2],
[4, 1]
])

simplices = Delaunay(points).simplices # 三角形中顶点的索引

plt.triplot(points[:, 0], points[:, 1], simplices)
plt.scatter(points[:, 0], points[:, 1], color=‘r’)

plt.show()
输出
注：三角形顶点的 id 存储在三角剖分对象的 simplices 属性中。

凸包
凸包（Convex Hull）是一个计算几何（图形学）中的概念。

在一个实数向量空间 V 中，对于给定集合 X，所有包含 X 的凸集的交集 S 被称为 X 的凸包。X 的凸包可以用 X 内所有点(X1，…Xn)的凸组合来构造。

我们可以使用 ConvexHull() 方法来创建凸包。
实例
通过给定的点来创建凸包：

import numpy as np
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt

points = np.array([
[2, 4],
[3, 4],
[3, 0],
[2, 2],
[4, 1],
[1, 2],
[5, 0],
[3, 1],
[1, 2],
[0, 2]
])

hull = ConvexHull(points)
hull_points = hull.simplices

plt.scatter(points[:,0], points[:,1])
for simplex in hull_points:
plt.plot(points[simplex,0], points[simplex,1], ‘k-’)

plt.show()

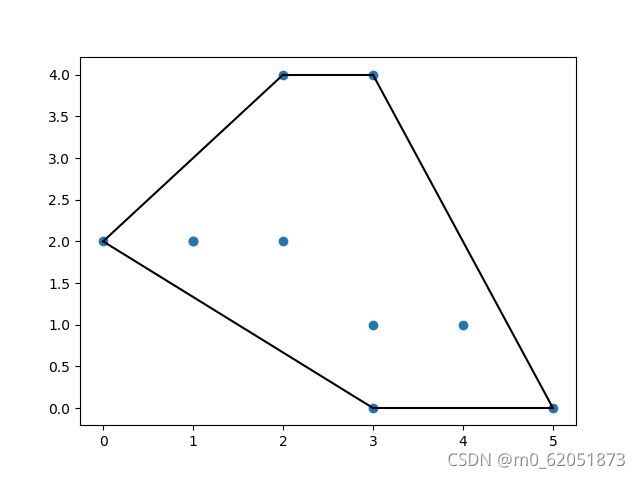
K-D 树
kd-tree（k-dimensional树的简称），是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。

K-D 树可以使用在多种应用场合，如多维键值搜索（范围搜寻及最邻近搜索）。

最邻近搜索用来找出在树中与输入点最接近的点。

KDTree() 方法返回一个 KDTree 对象。

query() 方法返回最邻近距离和最邻近位置。
实例
查找到 (1,1) 的最邻近距离:

from scipy.spatial import KDTree

points = [(1, -1), (2, 3), (-2, 3), (2, -3)]

kdtree = KDTree(points)

res = kdtree.query((1, 1))

print(res)
输出结果如下图所示：

(2.0, 0)
距离矩阵
在数学中, 一个距离矩阵是一个各项元素为点之间距离的矩阵（二维数组）。因此给定 N 个欧几里得空间中的点，其距离矩阵就是一个非负实数作为元素的 N×N 的对称矩阵距离矩阵和邻接矩阵概念相似，其区别在于后者仅包含元素（点）之间是否有连边，并没有包含元素（点）之间的连通的距离的讯息。因此，距离矩阵可以看成是邻接矩阵的加权形式。

举例来说，我们分析如下二维点 a 至 f。在这里，我们把点所在像素之间的欧几里得度量作为距离度量。
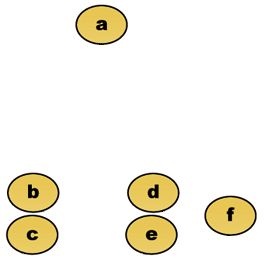
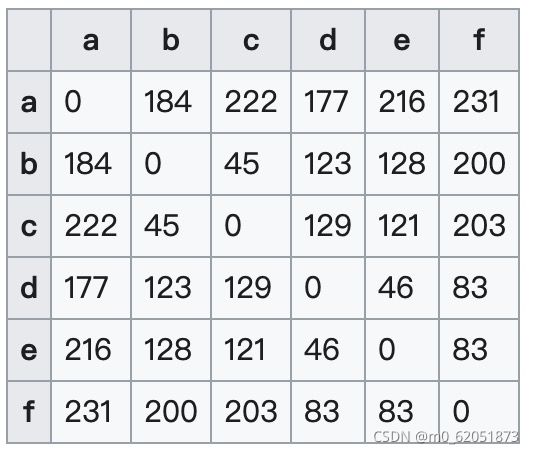距离矩阵的这些数据可以进一步被看成是图形表示的热度图（如下图所示），其中黑色代表距离为零，白色代表最大距离。

在生物信息学中，距离矩阵用来表示与坐标系无关的蛋白质结构，还有序列空间中两个序列之间的距离。这些表示被用在结构比对，序列比对，还有在核磁共振，X射线和结晶学中确定蛋白质结构。
欧几里得距离
在数学中，欧几里得距离或欧几里得度量是欧几里得空间中两点间"普通"（即直线）距离。使用这个距离，欧氏空间成为度量空间。相关联的范数称为欧几里得范数。较早的文献称之为毕达哥拉斯度量。

欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

以下实例查看给定点之间的欧几里德距离：
实例
from scipy.spatial.distance import euclidean

p1 = (1, 0)
p2 = (10, 2)

res = euclidean(p1, p2)

print(res)
输出结果如下图所示：

9.21954445729
曼哈顿距离
出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

曼哈顿距离只能上、下、左、右四个方向进行移动，并且两点之间的曼哈顿距离是两点之间的最短距离。

曼哈顿与欧几里得距离：红、蓝与黄线分别表示所有曼哈顿距离都拥有一样长度（12），而绿线表示欧几里得距离有6×√2 ≈ 8.48的长度。

以下实例通过给点的点计算曼哈顿距离：

实例
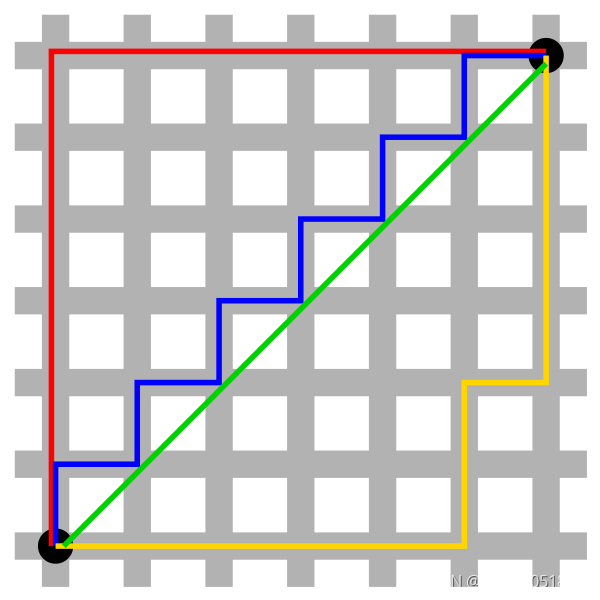
from scipy.spatial.distance import cityblock

p1 = (1, 0)
p2 = (10, 2)

res = cityblock(p1, p2)

print(res)
输出结果为：

11
余弦距离
余弦距离，也称为余弦相似度，通过测量两个向量的夹角的余弦值来度量它们之间的相似性。

0 度角的余弦值是 1，而其他任何角度的余弦值都不大于 1，并且其最小值是 -1。

以下实例计算 A 与 B 两点的余弦距离：

实例
from scipy.spatial.distance import cosine

p1 = (1, 0)
p2 = (10, 2)

res = cosine(p1, p2)

print(res)
输出结果为：

0.019419324309079777
汉明距离
在信息论中，两个等长字符串之间的汉明距离（英语：Hamming distance）是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。

汉明重量是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。

1011101与1001001之间的汉明距离是2。
2143896与2233796之间的汉明距离是3。
"toned"与"roses"之间的汉明距离是3。
以下实例计算两个点之间的汉明距离：

实例
from scipy.spatial.distance import hamming

p1 = (True, False, True)
p2 = (False, True, True)

res = hamming(p1, p2)

print(res)
输出结果为：

0.666666666667

4.5 SciPy Matlab 数组

NumPy 提供了 Python 可读格式的数据保存方法。

SciPy 提供了与 Matlab 的交互的方法。

SciPy 的 scipy.io 模块提供了很多函数来处理 Matlab 的数组。
以 Matlab 格式导出数据
savemat() 方法可以导出 Matlab 格式的数据。

该方法参数有：
filename - 保存数据的文件名。
mdict - 包含数据的字典。
do_compression - 布尔值，指定结果数据是否压缩。默认为 False。
将数组作为变量 “vec” 导出到 mat 文件：

实例
from scipy import io
import numpy as np

arr = np.arange(10)

io.savemat(‘arr.mat’, {“vec”: arr})
注意：上面的代码会在您的计算机上保存了一个名为 “arr.mat” 的文件。
导入 Matlab 格式数据
loadmat() 方法可以导入 Matlab 格式数据。

该方法参数：

filename - 保存数据的文件名。
返回一个结构化数组，其键是变量名，对应的值是变量值。

以下实例从 mat 文件中导入数组：

实例
from scipy import io
import numpy as np

arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9,])

导出
io.savemat(‘arr.mat’, {“vec”: arr})

导入
mydata = io.loadmat(‘arr.mat’)

print(mydata)
返回结果如下：

{
‘header’: b’MATLAB 5.0 MAT-file Platform: nt, Created on: Tue Sep 22 13:12:32 2020’,
‘version’: ‘1.0’,
‘globals’: [],
‘vec’: array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]])
}使用变量名 “vec” 只显示 matlab 数据的数组：
实例
from scipy import io
import numpy as np

arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9,])

导出
io.savemat(‘arr.mat’, {“vec”: arr})

导入
mydata = io.loadmat(‘arr.mat’)

print(mydata[‘vec’])
返回结果如下：

[[0 1 2 3 4 5 6 7 8 9]]
从结果可以看出数组最初是一维的，但在提取时它增加了一个维度，变成了二维数组。

解决这个问题可以传递一个额外的参数 squeeze_me=True：

实例
from scipy import io
import numpy as np

arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9,])

导出
io.savemat(‘arr.mat’, {“vec”: arr})

导入
mydata = io.loadmat(‘arr.mat’, squeeze_me=True)

print(mydata[‘vec’])
返回结果如下：

[0 1 2 3 4 5 6 7 8 9]

4.6SciPy 插值

什么是插值？
在数学的数值分析领域中，插值（英语：interpolation）是一种通过已知的、离散的数据点，在范围内推求新数据点的过程或方法。

简单来说插值是一种在给定的点之间生成点的方法。

例如：对于两个点 1 和 2，我们可以插值并找到点 1.33 和 1.66。

插值有很多用途，在机器学习中我们经常处理数据缺失的数据，插值通常可用于替换这些值。

这种填充值的方法称为插补。

除了插补，插值经常用于我们需要平滑数据集中离散点的地方。
如何在 SciPy 中实现插值？
SciPy 提供了 scipy.interpolate 模块来处理插值。

一维插值
一维数据的插值运算可以通过方法 interp1d() 完成。
该方法接收两个参数 x 点和 y 点。

返回值是可调用函数，该函数可以用新的 x 调用并返回相应的 y，y = f(x)。

对给定的 xs 和 ys 插值，从 2.1、2.2… 到 2.9：

实例
from scipy.interpolate import interp1d
import numpy as np

xs = np.arange(10)
ys = 2*xs + 1

interp_func = interp1d(xs, ys)

newarr = interp_func(np.arange(2.1, 3, 0.1))

print(newarr)
输出结果为：

[5.2 5.4 5.6 5.8 6. 6.2 6.4 6.6 6.8]
注意：新的 xs 应该与旧的 xs 处于相同的范围内，这意味着我们不能使用大于 10 或小于 0 的值调用 interp_func()。
单变量插值
在一维插值中，点是针对单个曲线拟合的，而在样条插值中，点是针对使用多项式分段定义的函数拟合的。

单变量插值使用 UnivariateSpline() 函数，该函数接受 xs 和 ys 并生成一个可调用函数，该函数可以用新的 xs 调用。

分段函数，就是对于自变量 x 的不同的取值范围，有着不同的解析式的函数。

为非线性点找到 2.1、2.2…2.9 的单变量样条插值：
实例
from scipy.interpolate import UnivariateSpline
import numpy as np

xs = np.arange(10)
ys = xs**2 + np.sin(xs) + 1

interp_func = UnivariateSpline(xs, ys)

newarr = interp_func(np.arange(2.1, 3, 0.1))

print(newarr)
输出结果为：

[5.62826474 6.03987348 6.47131994 6.92265019 7.3939103 7.88514634
8.39640439 8.92773053 9.47917082]
径向基函数插值
径向基函数是对应于固定参考点定义的函数。

曲面插值里我们一般使用径向基函数插值。

Rbf() 函数接受 xs 和 ys 作为参数，并生成一个可调用函数，该函数可以用新的 xs 调用。

实例
from scipy.interpolate import Rbf
import numpy as np

xs = np.arange(10)
ys = xs**2 + np.sin(xs) + 1

interp_func = Rbf(xs, ys)

newarr = interp_func(np.arange(2.1, 3, 0.1))

print(newarr)
输出结果为：

[6.25748981 6.62190817 7.00310702 7.40121814 7.8161443 8.24773402
8.69590519 9.16070828 9.64233874]

4.7 Scipy 显著性检验

显著性检验（significance test）就是事先对总体（随机变量）的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设（备择假设）是否合理，即判断总体的真实情况与原假设是否有显著性差异。或者说，显著性检验要判断样本与我们对总体所做的假设之间的差异是纯属机会变异，还是由我们所做的假设与总体真实情况之间不一致所引起的。显著性检验是针对我们对总体所做的假设做检验，其原理就是"小概率事件实际不可能性原理"来接受或否定假设。
显著性检验即用于实验处理组与对照组或两种不同处理的效应之间是否有差异，以及这种差异是否显著的方法。

SciPy 提供了 scipy.stats 的模块来执行Scipy 显著性检验的功能。
统计假设
统计假设是关于一个或多个随机变量的未知分布的假设。随机变量的分布形式已知，而仅涉及分布中的一个或几个未知参数的统计假设，称为参数假设。检验统计假设的过程称为假设检验，判别参数假设的检验称为参数检验。
零假设
零假设（null hypothesis），统计学术语，又称原假设，指进行统计检验时预先建立的假设。零假设成立时，有关统计量应服从已知的某种概率分布。

当统计量的计算值落入否定域时，可知发生了小概率事件，应否定原假设。

常把一个要检验的假设记作 H0，称为原假设（或零假设） (null hypothesis) ，与 H0 对立的假设记作 H1，称为备择假设(alternative hypothesis) 。

在原假设为真时，决定放弃原假设，称为第一类错误，其出现的概率通常记作 α；
在原假设不真时，决定不放弃原假设，称为第二类错误，其出现的概率通常记作 β
α+β 不一定等于 1。
通常只限定犯第一类错误的最大概率 α，不考虑犯第二类错误的概率 β。这样的假设检验又称为显著性检验，概率 α 称为显著性水平。

最常用的 α 值为 0.01、0.05、0.10 等。一般情况下，根据研究的问题，如果放弃真假设损失大，为减少这类错误，α 取值小些，反之，α 取值大些。
备择假设
备择假设(alternative hypothesis)是统计学的基本概念之一，其包含关于总体分布的一切使原假设不成立的命题。备择假设亦称对立假设、备选假设。

备择假设可以替代零假设。

例如我们对于学生的评估，我们将采取：

“学生比平均水平差” -— 作为零假设

“学生优于平均水平” —— 作为替代假设。

单边检验
单边检验(one-sided test)亦称单尾检验，又称单侧检验，在假设检验中，用检验统计量的密度曲线和二轴所围成面积中的单侧尾部面积来构造临界区域进行检验的方法称为单边检验。

当我们的假设仅测试值的一侧时，它被称为"单尾测试"。

例子：

对于零假设：

“均值等于 k”
我们可以有替代假设：

“平均值小于 k”
或
“平均值大于 k”
双边检验
边检验(two-sided test)，亦称双尾检验、双侧检验.在假设检验中，用检验统计量的密度曲线和x轴所围成的面积的左右两边的尾部面积来构造临界区域进行检验的方法。

当我们的假设测试值的两边时。

例子：

对于零假设：

“均值等于 k”
我们可以有替代假设：

“均值不等于k”
在这种情况下，均值小于或大于 k，两边都要检查。
阿尔法值
阿尔法值是显著性水平。

显著性水平是估计总体参数落在某一区间内，可能犯错误的概率，用 α 表示。

数据必须有多接近极端才能拒绝零假设。

通常取为 0.01、0.05 或 0.1。
P 值
P 值表明数据实际接近极端的程度。
比较 P 值和阿尔法值(alpha)来确定统计显著性水平。

如果 p 值 <= alpha，我们拒绝原假设并说数据具有统计显著性，否则我们接受原假设。
T 检验（T-Test）
T 检验用于确定两个变量的均值之间是否存在显著差异，并判断它们是否属于同一分布。

这是一个双尾测试。

函数 ttest_ind() 获取两个相同大小的样本，并生成 t 统计和 p 值的元组。

查找给定值 v1 和 v2 是否来自相同的分布：

实例
import numpy as np
from scipy.stats import ttest_ind

v1 = np.random.normal(size=100)
v2 = np.random.normal(size=100)

res = ttest_ind(v1, v2)

print(res)
输出结果为：

Ttest_indResult(statistic=0.40833510339674095, pvalue=0.68346891833752133)
如果只想返回 p 值，请使用 pvalue 属性：

实例
import numpy as np
from scipy.stats import ttest_ind

v1 = np.random.normal(size=100)
v2 = np.random.normal(size=100)

res = ttest_ind(v1, v2).pvalue

print(res)
输出结果为：

0.68346891833752133
KS 检验
KS 检验用于检查给定值是否符合分布。
该函数接收两个参数；测试的值和 CDF。

CDF 为累积分布函数(Cumulative Distribution Function)，又叫分布函数。

CDF 可以是字符串，也可以是返回概率的可调用函数。

它可以用作单尾或双尾测试。

默认情况下它是双尾测试。我们可以将参数替代作为两侧、小于或大于其中之一的字符串传递。

查找给定值是否符合正态分布：
import numpy as np
from scipy.stats import kstest

v = np.random.normal(size=100)

res = kstest(v, ‘norm’)

print(res)
输出结果为：

KstestResult(statistic=0.047798701221956841, pvalue=0.97630967161777515)
数据统计说明
使用 describe() 函数可以查看数组的信息，包含以下值：

nobs – 观测次数
minmax – 最小值和最大值
mean – 数学平均数
variance – 方差
skewness – 偏度
kurtosis – 峰度
显示数组中的统计描述信息：

实例
import numpy as np
from scipy.stats import describe

v = np.random.normal(size=100)
res = describe(v)

print(res)
输出结果为：

DescribeResult(
nobs=100,
minmax=(-2.0991855456740121, 2.1304142707414964),
mean=0.11503747689121079,
variance=0.99418092655064605,
skewness=0.013953400984243667,
kurtosis=-0.671060517912661
)
正态性检验（偏度和峰度）
利用观测数据判断总体是否服从正态分布的检验称为正态性检验，它是统计判决中重要的一种特殊的拟合优度假设检验。

正态性检验基于偏度和峰度。

normaltest() 函数返回零假设的 p 值：

“x 来自正态分布”
偏度
数据对称性的度量。

对于正态分布，它是 0。

如果为负，则表示数据向左倾斜。

如果是正数，则意味着数据是正确倾斜的。

峰度
衡量数据是重尾还是轻尾正态分布的度量。

正峰度意味着重尾。

负峰度意味着轻尾。

查找数组中值的偏度和峰度：
实例
import numpy as np
from scipy.stats import skew, kurtosis

v = np.random.normal(size=100)

print(skew(v))
print(kurtosis(v))
输出结果为：

0.11168446328610283
-0.1879320563260931

查找数据是否来自正态分布：

实例
import numpy as np
from scipy.stats import normaltest

v = np.random.normal(size=100)

print(normaltest(v))
输出结果为：

NormaltestResult(statistic=4.4783745697002848, pvalue=0.10654505998635538)

5.stasmodels

6.scikit-learn

如何改变文本的样式

强调文本 强调文本

加粗文本 加粗文本

标记文本

~~删除文本~~

引用文本

H₂O is是液体。

2¹⁰ 运算结果是 1024.

插入链接与图片

链接: link.

图片:

带尺寸的图片:

居中的图片:

居中并且带尺寸的图片:

当然，我们为了让用户更加便捷，我们增加了图片拖拽功能。

如何插入一段漂亮的代码片

去博客设置在这里插入代码片页面，选择一款你喜欢的代码片高亮样式，下面展示同样高亮的 代码片.

// An highlighted block
var foo = 'bar';

生成一个适合你的列表

项目
- 项目
  - 项目

项目1
项目2
项目3

计划任务
完成任务

创建一个表格

一个简单的表格是这么创建的：

项目	Value
电脑	$1600
手机	$12
导管	$1

设定内容居中、居左、居右

使用:---------:居中
使用:----------居左
使用----------:居右

第一列	第二列	第三列
第一列文本居中	第二列文本居右	第三列文本居左

SmartyPants

SmartyPants将ASCII标点字符转换为“智能”印刷标点HTML实体。例如：

TYPE	ASCII	HTML
Single backticks	`'Isn't this fun?'`	‘Isn’t this fun?’
Quotes	`"Isn't this fun?"`	“Isn’t this fun?”
Dashes	`-- is en-dash, --- is em-dash`	– is en-dash, — is em-dash

创建一个自定义列表

Markdown

Text-to- HTML conversion tool

Authors

John

Luke

如何创建一个注脚

一个具有注脚的文本。¹

注释也是必不可少的

Markdown将文本转换为 HTML。

KaTeX数学公式

您可以使用渲染LaTeX数学表达式 KaTeX:

Gamma公式展示 $\Gamma(n) = (n-1)!\quad\forall n\in\mathbb N$ 是通过欧拉积分

$\Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt\,.$

你可以找到更多关于的信息 LaTeX 数学表达式here.

新的甘特图功能，丰富你的文章

Mon 06 Mon 13 Mon 20 已完成进行中计划一计划二现有任务 Adding GANTT diagram functionality to mermaid

关于 甘特图 语法，参考这儿,

UML 图表

可以使用UML图表进行渲染。 Mermaid. 例如下面产生的一个序列图：

张三李四王五你好！李四, 最近怎么样? 你最近怎么样，王五？我很好，谢谢! 我很好，谢谢! 李四想了很长时间, 文字太长了不适合放在一行. 打量着王五... 很好... 王五, 你怎么样? 张三李四王五

这将产生一个流程图。:

链接

长方形

圆

圆角长方形

菱形

关于 Mermaid 语法，参考这儿,

FLowchart流程图

我们依旧会支持flowchart的流程图：

Created with Raphaël 2.3.0 开始我的操作确认？结束 yes no

关于 Flowchart流程图 语法，参考这儿.

导出与导入

导出

如果你想尝试使用此编辑器, 你可以在此篇文章任意编辑。当你完成了一篇文章的写作, 在上方工具栏找到 文章导出 ，生成一个.md文件或者.html文件进行本地保存。

导入

如果你想加载一篇你写过的.md文件，在上方工具栏可以选择导入功能进行对应扩展名的文件导入，
继续你的创作。

注脚的解释 ↩︎

python数据分析初学

PYTHON数据分析小白学习

1.numpy

1.2有关数组的属性和函数

1.3 数组元素的获取

1.4统计函数与线性代数运算

1.5 随机数生成

2.pandas

2.1 前期准备

2.2 pandas 数据结构 ——Series

2.3 dataframe

2.4 csv 文件

Column Non-Null Count Dtype # 各列的数据类型

2.5 JSON

2.6 数据清洗

3.matplotlib

3.1 matplotlib pyplot

3.2Matplotlib 绘图标记

3.3Matplotlib 绘图线

3.4Matplotlib 轴标签和标题

3.5 Matplotlib 网格线

3.6Matplotlib 绘制多图

3.7 matplotlib 散点图

3.8 matplotlib 柱形图

3.8 matplotlib 饼图

4.scipy

4.1 scipy 优化器

最小化函数

4.2 SciPy 稀疏矩阵

4.3 scipy图结构

4.4scipy空间数据

4.5 SciPy Matlab 数组

4.6SciPy 插值

4.7 Scipy 显著性检验

5.stasmodels

6.scikit-learn

如何改变文本的样式

插入链接与图片

如何插入一段漂亮的代码片

生成一个适合你的列表

创建一个表格

设定内容居中、居左、居右

SmartyPants

创建一个自定义列表

如何创建一个注脚

注释也是必不可少的

KaTeX数学公式

新的甘特图功能，丰富你的文章

UML 图表

FLowchart流程图

导出与导入

导出

导入

你可能感兴趣的:(python,数据分析)