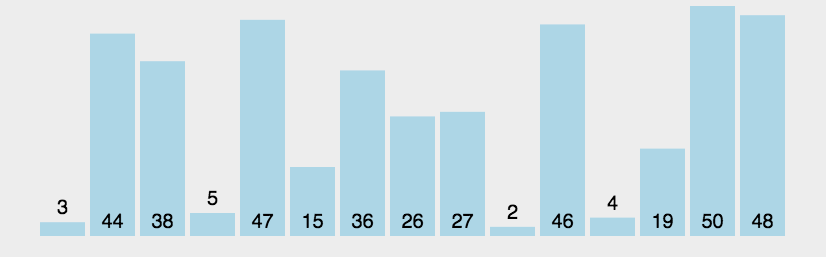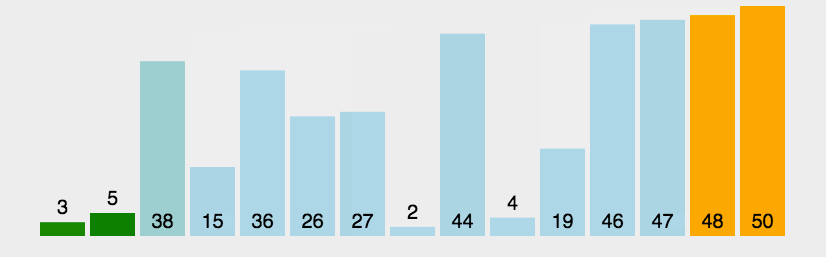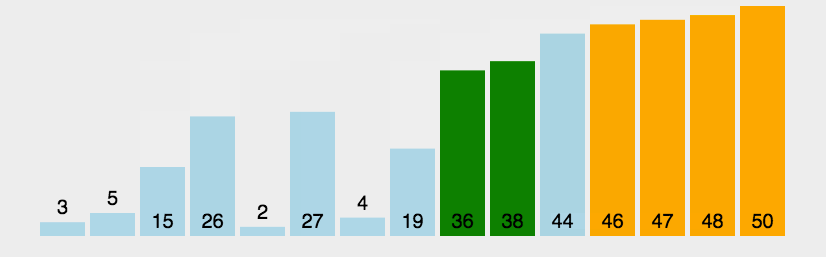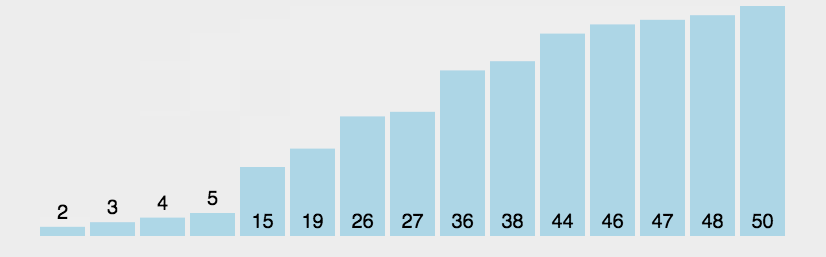C语言 几种排序方法（冒泡、选择、插入、归并、快速）

1.冒泡排序

它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

算法步骤 比较相邻的元素。如果第一个比第二个大，就交换他们两个。 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个。 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

执行过程：

# include 
# include 
int main(void)
{
    int arr[] = {5, 2, 3, -8, 34, 76, 32, 43, 0, -70, 35, 543, 6};
    int len= sizeof(arr) / sizeof(arr[0]);;  
    int i;  //比较的轮数
    int j;  //每轮比较的次数
    int temp;  //交换数据时用于存放中间数据
    for (i=0; i<len-1; ++i)  //比较n-1轮
    {
        for (j=0; j<len-1-i; ++j)  //每轮比较n-1-i次,
        {
            if (arr[j] < arr[j+1])
            {
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
    printf("排序后:\n");
    for (i=0; i<len; ++i)
    {
        printf("%d\x20", arr[i]);
    }
    printf("\n");
    return 0;
}

2.选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

算法步骤 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
再从剩余未排序元素中继续
寻找最小（大）元素，然后放到已排序序列的末尾。

重复第二步，直到所有元素均排序完毕。
代码：

#include 
# include 

int main() {
        int arr[] = { 5, 2, 3, -8, 34, 76, 32, 43, 0, -70, 35, 543, 6};
        int len = (int) sizeof(arr) / sizeof(*arr);
        
       int i, j, temp;
        for (i = 0; i < len - 1; i++)
                for (j = 0; j < len - 1 - i; j++)
                        if (arr[j] > arr[j + 1]) { 
                                temp = arr[j];
                                arr[j] = arr[j + 1];
                                arr[j + 1] = temp;
                        }
                        
       
        for (i = 0; i < len; i++)
                printf("%d ", arr[i]);
        return 0;
}

3.插入排序

插入排序，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法 [1] 。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动 [2] 。

1. 算法步骤 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
   从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

#include 
# include 

int main(){
     int arr[] = { 5, 2, 3, -8, 34, 76, 32, 43, 0, -70, 35, 543, 6};
  int len = (int) sizeof(arr) / sizeof(*arr);
  
  
	int i,j,x; 
    for( i= 1; i<len; i++){
        if(arr[i] < arr[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
             j= i-1;
             x = arr[i];
            while(j>-1 && x < arr[j]){  //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = x;      //插入到正确位置
        }

}


    for(j=0; j<len; j++){
        printf("%d ",arr[j]);
    }
    printf("\n");
    
    
    
    return 0;
}

4.归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：
自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
自下而上的迭代；

算法步骤 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

设定两个指针，最初位置分别为两个已经排序序列的起始位置；

比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

重复步骤 3 直到某一指针达到序列尾；

将另一序列剩下的所有元素直接复制到合并序列尾。
#include
#define MAXSIZE 10

// 递归的方式实现归并排序

// 实现归并，并把结果存放到list1

# include 
#include 
void merging(int *list1, int list1_size, int *list2, int list2_size) {
    int i,j,k, m;
    int temp[MAXSIZE];

    i = j = k = 0;

    while(i < list1_size && j < list2_size)
    {
        if(list1[i] < list2[j])
        {
            temp[k] = list1[i];
            k++;
            i++;
        }
        else
        {
            temp[k++] = list2[j++];
        }
    }

    while(i < list1_size)
    {
        temp[k++] = list1[i++];
    }

    while(j < list2_size)
    {
        temp[k++] = list2[j++];
    }

    for(m = 0;m < (list1_size + list2_size);m++)
    {
        list1[m] = temp[m];
    } }

void MergeSort(int k[], int n) {
    if(n > 1)
    {
        /*
        *list1是左半部分，list2是右半部分
        */
        int *list1 = k;
        int list1_size = n/2;
        int *list2 = k + list1_size;
        int list2_size = n - list1_size;

        MergeSort(list1, list1_size);
        MergeSort(list2, list2_size);

        // 把两个合在一起
        merging(list1, list1_size, list2, list2_size);
    }

}

int main() {
    int i, arr[] = { 5, 2, 3, -8, 34, 76, 32, 43, 0, -70, 35, 543, 6};    int len = (int) sizeof(arr) / sizeof(*arr); 
    MergeSort(arr, len);

    printf("排序后的结果是：");

    for(i = 0;i < len;i++)
    {
        printf("%d", a[i]);
    }
    printf("\n\n");

    return 0; 
}

5.快速排序

原理:
   快速排序,给基准数据找其正确索引位置的过程.
   如下图所示,假设最开始的基准数据为数组第一个元素23,则首先用一个临时变量去存储基准数据,即tmp=23;然后分别从数组的两端扫描数组，设两个指示标志:low指向起始位置，high指向末尾.
   如果扫描到的值大于基准数据就让high减1,如果发现有元素比该基准数据的值小(如上图中18<=tmp)，就将high位置的值赋值给low位置。
   如果扫描到的值小于基准数据就让low加1,如果发现有元素大于基准数据的值(如上图46=>tmp)，就再将low位置的值赋值给high位置的值.

算法步骤 从数列中挑出一个元素，称为 “基准”（pivot）;

重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

#include "stdio.h"

typedef struct _Range {
    int start, end;    //开始指向分别指向两端 
} Range;

Range new_Range(int s, int e) {
    Range r;
    r.start = s;     //开始指向需要排序数组的两端 
    r.end = e;
    return r;   //返回一个结构体 
}

void swap(int *x, int *y) {   //交换数据函数 
    int t = *x;
    *x = *y;
    *y = t;
}

void quick_sort(int arr[], const int len) {
    if (len <= 0)
        return;    //保证数据长度大于0 

    Range r[len];
    int p = 0;
    r[p++] = new_Range(0, len - 1);
    while (p) {
        Range range = r[--p];
        if (range.start >= range.end)
            continue;
        int mid = arr[(range.start + range.end) / 2]; // 选取中间点作为基准点 
        int left = range.start, right = range.end;
        do {
            while (arr[left] < mid) ++left;   // 检测基准点左侧是否符合要求
            while (arr[right] > mid) --right; //检测基准点右侧是否符合要求
            if (left <= right) {
                swap(&arr[left], &arr[right]);
                left++;
                right--;               // 移動指針以繼續
            }
        } while (left <= right);
        if (range.start < right) r[p++] = new_Range(range.start, right);
        if (range.end > left) r[p++] = new_Range(left, range.end);
    }
}

int main()
{
	int j;
	  int arr[] = { 5, 2, 3, -8, 34, 76, 32, 43, 0, -70, 35, 543, 6};
        int len = (int) sizeof(arr) / sizeof(*arr);
        quick_sort(arr,len);
            for(j=0; j<len; j++){
        printf("%d ",arr[j]);
    }
    printf("\n");
        
}