通俗易懂的方式讲解最大流和最小割问题

本文为CSDN博主「冰岛少年」的原创文章，博主逻辑太强了。
原文链接：https://blog.csdn.net/weixin_43710268/article/details/106041181
————————————————

最大流问题：

标号作用：
1）圈内的标号，为点的代号，如s，t；
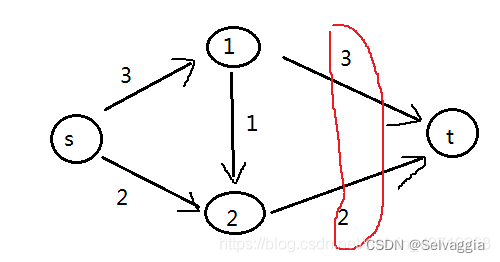
2）边上的标号，如3/0：3为容量，表示两个点之间最大流通量；0为当前实际流通量。

问题：我们想要让水从s流向t，那么最大有多少水能流到t呢？

先粗略一看，水要从s到t肯定要经过（1，t），（2，t）这两条通道；那么受这两条管道的限制只能流过3+2=5ml水，但因为流水量还受前面的管道的限制，所以这两条管道的实际流水量并不一定等于2+3=5ml；所以我们要求出从s到t的最大流水量，我们就需要求出流过（1，t），（2，t）这两条通道的水量，即流入t的实际流水量；

求解步骤很简单：
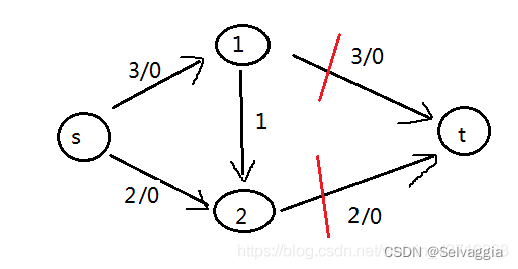
1）、先在（s，1，t）这条路线流过3ml：

2）、再往（s，2，t）流过2ml：

可见，不能再流更多的水过去了，因此最大流通量为3+2=5ml；

2、接下来我们尝试再换个方式计算：
1）、先在（s，1，t）流过2ml；
2）、再（s，1，2，t）流过1ml；
3）、再（s，2，t）流过1ml；
现在的情况是下面这样的：

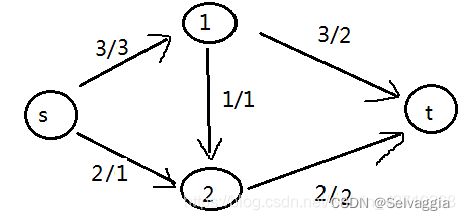
可见，现在的情况还没有达到最大流通量，那我们可以接着这样做：
4）、走（s，2，1，t）流过1ml；
解释：但是你会很奇怪，明明（1,2）这个通道已经被使用了啊？但其实我们走的是（2,1）这条通道，那我们怎么能反着箭头走呢？其实这就相当于把原来（1,2）方向通道内的水退回去了，退到点（1）处。
下面我们一步步完成（s，2，1，t）流过1ml这个过程：
这1ml水先流过（s，2）到达结点（2），再让（1,2）这条通道的水退到结点（1）去，往（1，t）走，这个时候由于（1,2）少了1ml水往这走，那么自然这1ml水也没有到达（2，t）这个通道，那么（2，t）当前通道的流通量减为1，还可以通过1ml，所以结点2的水可以走（2，t）到达t。

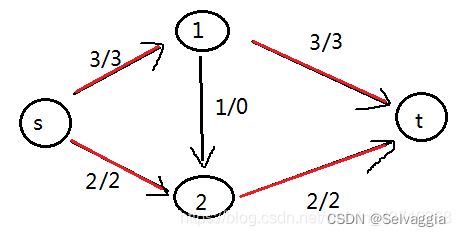
可以发现，最后的结果相同，最大流也为3+2=5；

那么我们可以总结一下，以上两个方法其实都是在寻找所有的增广链路，当找不到任何一条增广链路的时候，我们就能求出最大流通量。

所以接下来我们要引入几个概念：
链路：从两个顶点之间没有重复边的路径。
前向边：与链路方向一致的边，即你在这条边上想要的走向与边的箭头方向一致。
后向边：与链路方向相反的边。
增广链路：链路中所有前向边的当前流通量小于这条边的容量，即处于可以流通的状态，通道没有达到饱和；并且所有后向边的当前流通量大于0，即处于有水流过的状态。
可能，看了这些概念，你仍然想问那什么是增广链路呢？什么是前向边，后向边呢？我们重新来过一次找从s到t的路径的过程；

从这幅图可以看到，每一条路都没有被占用，我们走（s,1,t），（s,2,t），（s,1,2,t）这三条链路都能到达t，那么这三条路就是增广链路了。那用概念怎么理解呢？（s，1）,（1，t），（s，2），（2，t），（1，2）这些就是当前所有增广链路中的前向边，（1，s）,（t，1），（2，s），（t，2），（2,1）这些就是后向边。可见，这三条增广链路的所有边都是由前向边构成的，并且前向边的容量大于实际流通量0，可以流过水，即处于流通状态。

那么我们随机选一条增广链路走下去，我们选择（s,1,2,t）流过1ml，然后更新这一条增广链路上的流量。

那么此时的增广链路有哪些变化呢？此时能到达t的增广链路有（s，1，t），（s,2,t），（s，2,1，t）；
（s，1，t）和（s,2,t）中全是前向边，并且都是可以流通的，因此这两条肯定是增广链路。你们比较奇怪的是为什么（s，2,1，t）是增广链路，我们来分析一下，（s，2,1，t）中（s，2），（1，t）是可以流通的前向边，（2,1）这条边与箭头方向相反，箭头方向为（1,2），所以（2,1）在链路中是反向边，并且这条边实际流通量大于0，这也符合增广链路的定义；（s，2,1，t）这条链路就意味着我们可以将（1,2）这个地方的水退回到结点（1）处，让（1,2）这个方向的水往（1，t）走，而（s，2）流过来的水代替（1,2）这个地方的水到达结点2，补充结点2失去的（1,2）通道的水。
至此，我们已经完全认识到了这几个概念，下面讨论一下实现查找增广链路的算法；
以下面这幅图为例：

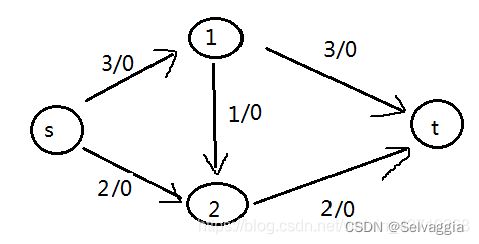
寻找增广链路求最大流的算法，Ford-Fulkerson算法：
我们这个图中共有4个顶点（s，1,2，t）；
现在先给点（s）进行标号（0，+），0表示点（s）是出发点，+表示输入的水流量为无穷大。
而剩下的点（1,2，t）为未标号的，如下图所示。

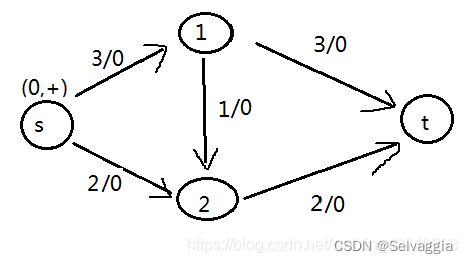
接下来，我们将点分为三类：
1）已标号已检查的：不存在，
2）已标号未检查的：包括点（s），
3）未标号的：包括点（1,2，t）。
然后我们从已标号未检查的集合拿到一个点，开始遍历整个图：
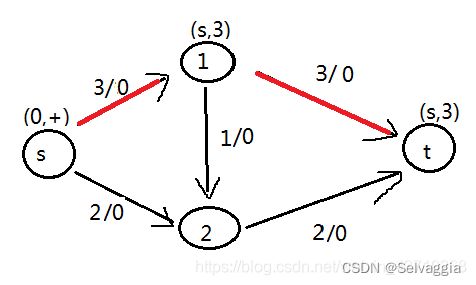
此时这个点为（s），对点（s）进行检查，检查的过程就是寻找点（s）的邻接点并加上标号，但这些邻接点与点（s）之间要满足一些要求，邻接点未标号，邻接点与点（s）之间的边是可以流通的前向边（即容量大于实际流通量的前向边），或者点之间的边不是零流的后向边（即实际流通量不为0的后向边）；并且，如果符合条件的邻接点中包含点（t），就说明找到了一条增广链路，结束整个遍历过程。可见满足要求的点只有（1）和（2）；我们对点（1）加上标号（s，3），代表从点（s）到点（1）的可流通量为3；我们再对点（2）加上标号（s，2），代表从点（s）到点（2）的可流通量为2；
接下来把点（s）从已标号未检查的集合中转移到已标号已检查的集合中，点（1）和点（2）从未标号的集合中转移到已标号未检查的集合中；
现在集合中的情况：
1）已标号已检查的：包括点（s），
2）已标号未检查的：包括点（1,2），
3）未标号的：包括点（t）。
然后再重复上面的过程，从已标号未检查的集合拿到一个点，继续检查，此刻拿到的点为（1），对符合条件的邻接点（t）和（2）进行标号，发现符合条件的邻接点中包含t，所以遍历结束，找到了一条增广链路（s，1，t）；

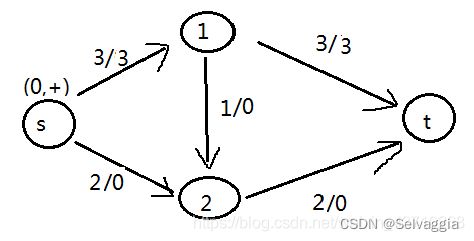
然后更新整条增广链路上的流量：比较这条路上的实际流通量的最小值，这个值就是这条路上的最大流通量。图中标号（s，3）的这个3就表示路径（s，1）的实际流通量为3。所以很明显这条路做多只能流通3，所以将0加上3,更新完毕。

这样就找到了一条增广链路了，然后我们再以这个图为基础寻找下一条，但是需要重新分过类，将所有点还原至未处理过的状态，但使用了的通道不还原。
接下来，我们将点分为三类：
1）已标号已检查的：不存在，
2）已标号未检查的：包括点（s），
3）未标号的：包括点（1,2，t）。

然后要做的就是从s开始重复检查的过程了，直至找到一条增广链路。
等到所有增广链路都被找出来后，将每一条增广链路的最大流通量相加就是整个图的最大流通量了。

最小割问题：割容量最小

对于上面这张图，我们想把s,t分割开，成为不连接的两部分，这个很简单，只需要断开（1，t），（2，t）就能成功，也有许多其它办法，例如：断开（s，1），（s，2），或者断开（s，1），（1，t），（2，t）。每割一条边就会产生损耗，这个损耗就是边的权值，我们想求出能将s,t割开的边，并且损耗达到最小，这就是求最小割；
上面这个图的最小割很明显就是将（1，t），（2，t）断开就是得到的最小割。

下面给出用最大流求最小割问题的方法：转换原理就是最小割的代价等于最大流。
原理：当一个图被割分成两个部分时，不再存在S到T的通路，所以割的代价必定大于等于图的最大流。
下面将这个原理演示一遍：
增广链路无合并的情况：

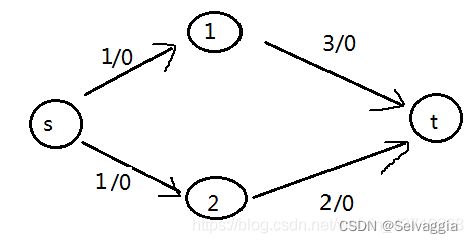
如果要将s与t断开成为两部分，很明显，我们可以直接断开（1，t），（2，t）就能做到，因为这两条路是从s通往t的必经之路；但我们也可以按照最大流的思想去做，有两条增广链路，（s，1，t），（s，2，t）可以通往t，我们只要把所有链路堵住就好了，那我们堵哪里呢？毫无疑问，要想使得损耗最小，肯定是只要分别堵住两条链路中管道容量最小的边即可，使得这些边的权值的和最小，这就让最小割的代价最小了，而每条增广链路的最大流通量的权值和也是最大流通量。这就说明了最小割的代价是等于最大流通量的，所以割的代价是大于等于最大流通量的。
下面我们再考虑一下链路有合并的情况：

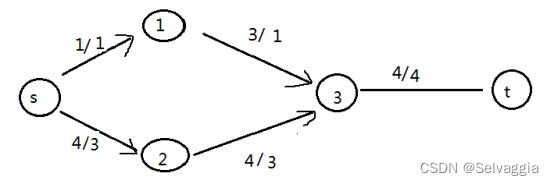
按照我们的想法：分别堵住两条链路中管道容量最小的边，我们堵住（s，1），（s，2），但此时损耗达到了1+4=5，但实际上最小损耗应切割（3，t），最小损耗明显为4。但尽管这样，最小割是等于最大流在这个图中仍然是正确的；所以，我们应该修改以下找最小割的方法，猜想一下，我们需要切割的应该是饱和边中的几条来达到最小割，饱和边有（s，1），（3，t）；所以我们先尝试切割边（s，1），形成新的图，再从这个新的图中求最大流b，如果这个图的最大流与原图a的最大流差值b-a等于被切割边（s，1）的容量1，那么就说明这条边是属于最小割集中的一条边。很明显b=4, a=4, a-b=0；而边（s，1）的容量为1，所以边（s，1）不属于最小割集。然后我们继续判断饱和边（3，t），在原图a上将（3，t）切除，形成新的图c，很明显c=0，a=4，a-c=4，符合，所以边（3，t）属于最小割集。遍历集合完毕，所以这幅图的最小割集为{ (3,t) }

所以当找到了最大流之后，就能从饱和边中找出最小割。最小割的值为最大流。