OpenCV/C++:点线面相关计算

之前也有一篇笔记，都比较简单，做个记录，方便速查。

C++&OpenCV：三角形插值、线面的交点_六月的翅膀的博客-CSDN博客

---

目录

1、向量的模

2、两点间距离（两点间的向量模） 

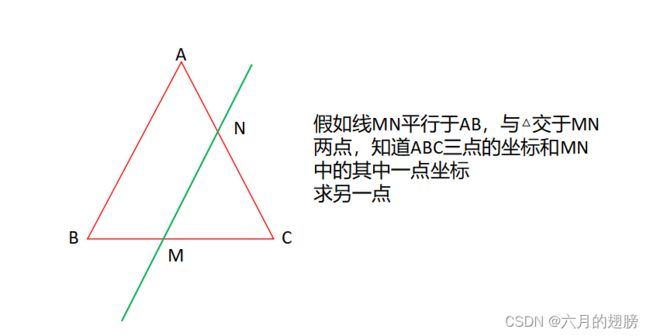
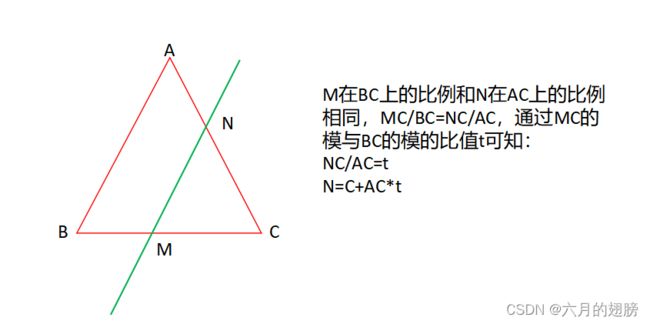
 3、求线段中某点坐标

 4、叉乘，平面法向量

 5、线面交点

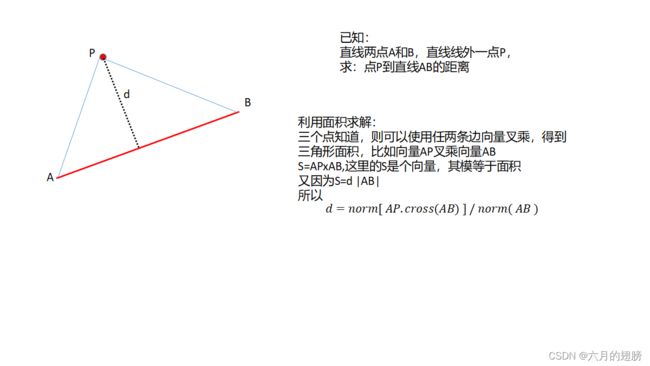
6、空间点到直线的距离

7、平面方程

8、两直线的交点

9、两向量的夹角

---

1、向量的模

int main()
{
    Vec3f A = Vec3f(10, 10, 1);
    cout << "向量A的模 = " << norm(A) << endl;
    Vec3f B = Vec3f(3, 3, 1);
    cout << "向量B的模 = " << norm(B) << endl;

    return 0;
}

 

2、两点间距离（两点间的向量模） 

int main()
{
    Vec3f A = Vec3f(10, 10, 1);
    Vec3f B = Vec3f(3, 3, 1);
    cout << "线段AB的长度为 = " << norm(A - B) << endl;
    //结果为6*根2
    return 0;
}

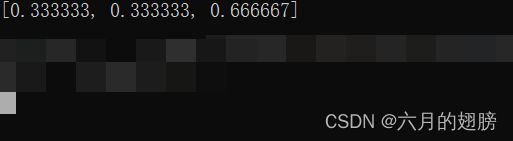
 3、求线段中某点坐标

int main()
{
    Vec3f A = Vec3f(0, 10, 0);
    Vec3f B = Vec3f(0, 0, 0);
    Vec3f C = Vec3f(10, 0, 0);
    Vec3f M = Vec3f(3, 0, 0);
    float t = norm(M - C) / norm(B - C);

    Vec3f N = C + (A - C) * t;
    cout << "N点坐标为：" << N << endl;
    return 0;
}

 

 4、叉乘，平面法向量

上面图中写错了，ON = OB.cross(OA)。右手定则

不仅点和叉写错了 方向还错了 /dog

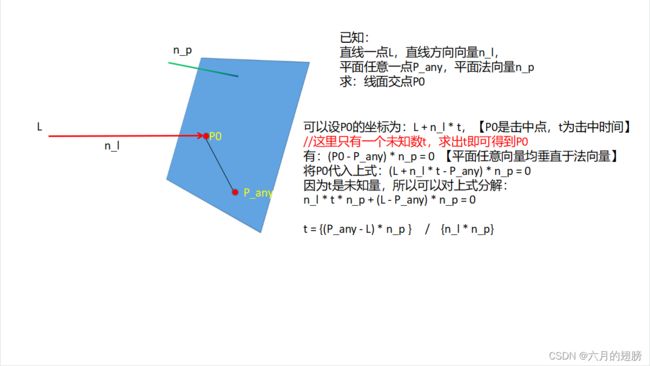
 5、线面交点

int main()
{
    //需要知道直线上一点和其方向向量，平面一点及其法向量
    Vec3f A=Vec3f(0, 1, 1);
    Vec3f B=Vec3f(1, 0, 1);
    Vec3f O=Vec3f(0, 0, 0);

    Vec3f M=Vec3f(1, 1, 0);
    Vec3f N=Vec3f(0, 0, 1);

    Vec3f line = M-N;//线方向向量，这里谁减谁都行
    Vec3f plane = (A - O).cross(B - O);//平面两个向量叉乘就是法向量
    
    float den = plane.dot(line);//面法向量乘线方向向量
    float t = plane.dot(A - N) / den;//A是面上一点，用B也可以
    Vec3f p0 = N + line * t;//这里线上的点用的N，也可以用M，只要上面求t的时候也是用的M就可以
    cout << p0 << endl;
    return 0;
}

 

---

//2023年1月10日 update

//2023年10月27日

 

cv::Point3d pointOfLinePlaneSolve(Point3d L_p, Point3d L_dir, Point3d P_p, Point3d P_norm)
    {
        //这种方法要求线的方向向量的yz值不能为0，因为涉及到除法
        Mat x = (cv::Mat_(3, 3) << P_norm.x, P_norm.y, P_norm.z,
            1, -L_dir.x / L_dir.y, 0,
            1, 0, -L_dir.x / L_dir.z);

        Mat y = (cv::Mat_(3, 1) << P_norm.dot(P_p),
            L_p.x - L_dir.x / L_dir.y * L_p.y,
            L_p.x - L_dir.x / L_dir.z * L_p.z
            );

        // 使用solve函数求解方程
        Mat coef;
        solve(x, y, coef, DECOMP_QR);

        return Point3d(coef);
    }

6、空间点到直线的距离

/// 

/// 
/// 
/// 线外一点
/// 线上点
/// 线上点
/// 
float getDist_P2L(Vec3f P, Vec3f A, Vec3f B)
{
    Vec3f PA = P - A;//线外点到线上一点的向量
    Vec3f Ldir = B - A;//直线的方向向量
    Vec3f Pnorm = PA.cross(Ldir);
    float S1 = norm(Ldir);
    float S2 = norm(Pnorm);
    return S2 / S1;
}

int main()
{
    Vec3f A = Vec3f(1.0, 0, 0);
    Vec3f B = Vec3f(0.0, 1.0, 0);
    Vec3f P = Vec3f(0.5, 0.5, 3);

    float dis = getDist_P2L(P, A, B);
    cout << dis << endl;
}

---

//2023年1月12日 update

7、平面方程

vector input;
vector coeffi;
void GetPanelEquation(vector& point3fArray)
{
    if (point3fArray.size() < 3)
    {
        cerr << "GetPanelEquation(...)函数中输入点的数量小于3." << endl;
    }
    float a,b,c,d;
    a = (point3fArray[1][1] - point3fArray[0][1])*(point3fArray[2][2] - point3fArray[0][2]) -
        (point3fArray[1][2] - point3fArray[0][2])*(point3fArray[2][1] - point3fArray[0][1]);
    
    b = (point3fArray[1][2] - point3fArray[0][2])*(point3fArray[2][0] - point3fArray[0][0]) -
        (point3fArray[1][0] - point3fArray[0][0])*(point3fArray[2][2] - point3fArray[0][2]);
    
    c = (point3fArray[1][0] - point3fArray[0][0])*(point3fArray[2][1] - point3fArray[0][1]) -
        (point3fArray[1][1] - point3fArray[0][1])*(point3fArray[2][0] - point3fArray[0][0]);
    
    d = 0 - (a * point3fArray[0][0] + b*point3fArray[0][1] + c*point3fArray[0][2]);
    coeffi.push_back(a);
    coeffi.push_back(b);
    coeffi.push_back(c);
    coeffi.push_back(d);
}

int main()
{
    input.push_back(Vec3f(100, 0, 0));
    input.push_back(Vec3f(0, 100, 0));
    input.push_back(Vec3f(0, 0, 3));
    GetPanelEquation(input);
    cout << "平面方程为："<< endl << coeffi[0] << " X + " << coeffi[1] << " Y + " << coeffi[2] << " Z + " << coeffi[3] << " = 0" << endl;
    if (abs(coeffi[3])>1e-6)
    {
        cout << "平面方程为：" << endl << -coeffi[0] / coeffi[3] << " X + " << -coeffi[1] / coeffi[3] << " Y + " << -coeffi[2] / coeffi[3] << " Z = 1" << endl;
    }
    return 1;
}

8、两直线的交点

        double r_xy12 = PointOnLine[0].x * PointOnLine[1].y - PointOnLine[1].x * PointOnLine[0].y;
		double r_x12 = PointOnLine[0].x - PointOnLine[1].x;
		double r_xy34 = PointOnLine[2].x * PointOnLine[3].y - PointOnLine[3].x * PointOnLine[2].y;
		double r_x34 = PointOnLine[2].x - PointOnLine[3].x;
		double r_y12 = PointOnLine[0].y - PointOnLine[1].y;
		double r_y34 = PointOnLine[2].y - PointOnLine[3].y;
		double fenmu = r_x12 * r_y34 - r_y12 * r_x34;

		GridPoint[i].x = (r_xy12 * r_x34 - r_x12 * r_xy34) / fenmu;
		GridPoint[i].y = (r_xy12 * r_y34 - r_y12 * r_xy34) / fenmu;

struct LinePara
{
	float k;
	float b;
};

// 获取直线参数  
void getLinePara(float& x1, float& y1, float& x2, float& y2, LinePara& LP)
{
	double m = 0;

	// 计算分子  
	m = x2 - x1;

	if (0 == m)
	{
		LP.k = 10000.0;
		LP.b = y1 - LP.k * x1;
	}
	else
	{
		LP.k = (y2 - y1) / (x2 - x1);
		LP.b = y1 - LP.k * x1;
	}


}

// 获取交点  
bool getCross(Point2f& p1, Point2f& p2, Point2f& p3, Point2f& p4, Point2f& pt) {

	LinePara para1, para2;
	getLinePara(p1.x, p1.y, p2.x, p2.y, para1);
	getLinePara(p3.x, p3.y, p4.x, p4.y, para2);

	pt.x = (para2.b - para1.b) / (para1.k - para2.k);
	pt.y = para1.k * pt.x + para1.b;
	// 判断是否平行  
	if (abs(para1.k - para2.k) > 0.5)
	{
		pt.x = (para2.b - para1.b) / (para1.k - para2.k);
		pt.y = para1.k * pt.x + para1.b;

		return true;

	}
	else
	{
		return false;
	}

}

9、两向量的夹角

template 
double getAngle3d(DataType _in1, DataType _in2)
{
	double theta2 = acos(_in1.dot(_in2) / (norm(_in1) * norm(_in2)));
	if (abs(_in1.dot(_in2)-1)<10e-6)//这里做个判断，否则nan
	{
		theta2 = 0;
	}
	else
	{
		theta2 = theta2 * 180 / acos(-1);
	}
	return theta2;
}