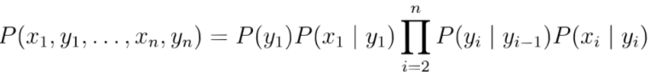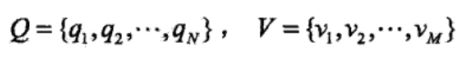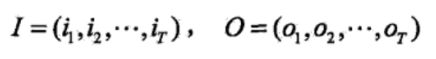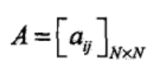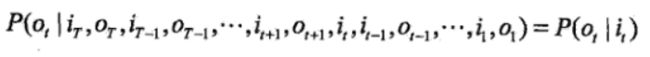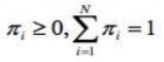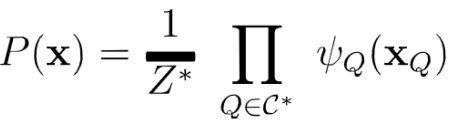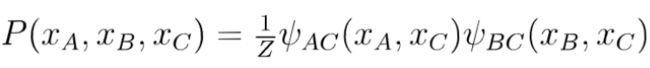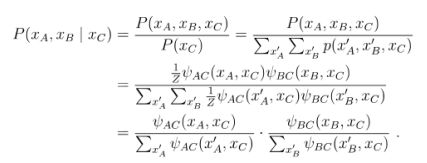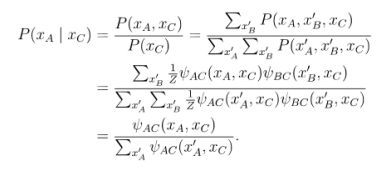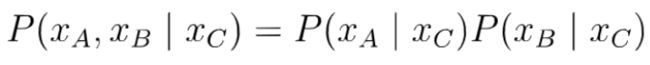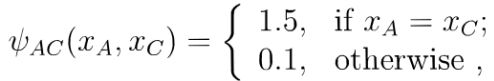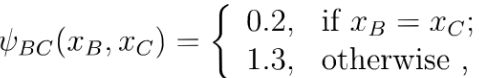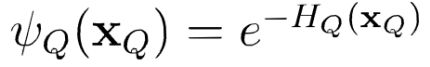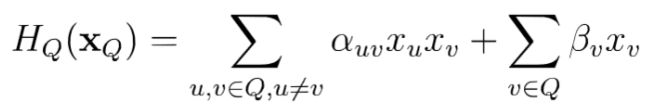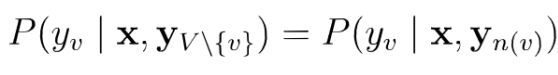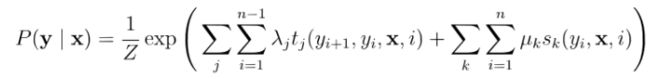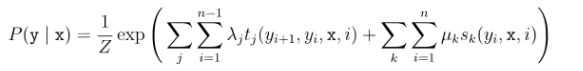机器学习---概率图模型（隐马尔可夫模型、马尔可夫随机场、条件随机场）

1. 隐马尔可夫模型

机器学习最重要的任务是根据已观察到的证据（例如训练样本）对感兴趣的未知变量（例如类别标

记）进行估计和推测。概率模型（probabilistic model）提供了一种描述框架，将描述任务归结为

计算变量的概率分布，在概率模型中，利用已知的变量推测未知变量的分布称为“推断

（inference）”，其核心在于基于可观测的变量推测出未知变量的条件分布。

生成式：计算联合分布(, , )，判别式：计算条件分布(, |)

符号约定：为关心的变量的集合，O为可观测变量集合，R为其他变量集合

概率模型直接利用概率求和规则消去变量R的时间和空间复杂度为指数级别(2^( +||))，需要一

种能够简洁紧凑表达变量间关系的工具。 

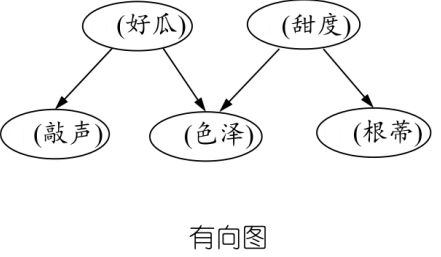
概率图模型(probabilistic graphical model)是一类用图来表达变量相关关系的概率模型。

图模型提供了一种描述框架，结点：随机变量（集合）；边：变量之间的依赖关系

分类：有向图：贝叶斯网，使用有向无环图表示变量之间的依赖关系

无向图：马尔可夫网，使用无向图表示变量间的相关关系

概率图模型分类：有向图：贝叶斯网，无向图：马尔可夫网

隐马尔可夫模型（Hidden Markov Model，HMM）组成：状态变量：，通常假定是

隐藏的，不可被观测的。取值范围为，通常有个可能取值的离散空间

观测变量：表示第 时刻的观测值集合，观测变量可以为离散或连续型，本章中只

讨论离散型观测变量，取值范围X为

隐马尔可夫模型（Hidden Markov Model，HMM）：时刻的状态  仅依赖于( − 1)，与其余

− 2个状态无关。马尔可夫链：系统下一时刻状态仅由当前状态决定，不依赖于以往的任何状态

HMM 的生成过程：

确定一个HMM需要三组参数 = [, , ] 。状态转移概率：模型在各个状态间转换的概率表示在任

意时刻t，若状态为si，下一状态为sj的概率

输出观测概率：模型根据当前状态获得各个观测值的概率。在任意时刻t，若状态为Si，则在下一

时刻状态为Sj的概率

初始状态慨率：模型在初始时刻各个状态出现的慨率

通过指定状态空间，观测空间和上述三组参数，就能确定一个隐马尔可夫模型。给定 = [, ,

] ，它按如下过程生成观察序列：

①设置 = 1, 并根据初始状态选择初始状态1

②根据 和输出观测概率 选择观测变量取值

③根据状态 和状态转移矩阵 转移模型状态，即确定+1

④若 < , 设置 = + 1，并转到②步，否则停止

HMM的基本问题：对于模型 = [, , ] ，给出具体应用定观测序列评估模型

和观测序列之间的匹配程度：有效计算观测序列其产生的概率

根据观测序列“推测”隐藏的模型状态y=

参数学习：如何调整模型参数 = [, , ] ，以使得该序列出现的概率最大

具体应用：根据以往的观测序列x=预测当前时刻最有可能的观测值；语音识别：根据观测的语音信

号推测最有可能的状态序列（即：对应的文字）；通过数据学习参数（模型训练)

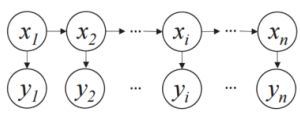
隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随

机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状

态的序列，称为状态序列(state sequence)：每个状态生成一个观测，而由此产生的观测的随机序

列，称为观测序列(observation sequence)。序列的每一个位置又可以看作是一个时刻。

隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。隐马尔可夫模型的形

式定义如下：设Q是所有可能的状态的集合，V是所有可能的观测的集合，

其中，N是可能的状态数，M是可能的观测数，I是长度为T的状态序列，O是对应的观测序列。

A是状态转移概率矩阵：

其中，是在时刻t处于状态qi的条件下在时刻t+1

转移到状态qj的概率。

B是观测概率矩阵：

其中，是在时刻t处于状态qj的条件下生成

观测vk的概率。π是初始状态概率向量：π=（πi），其中，是时刻t=1

处于状态qi的概率。

隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定。π和A决定状

态序列，B决定观测序列。因此，隐马尔可夫模型入可以用三元符号表示，即 = [, , ] ，, ,

称为隐马尔可夫模型的三要素。

齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态，

与其他时刻的状态及观测无关，也与时刻t无关。

观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态

无关。

例如，一段文字中名词、动词、形容词三类词出现的情况可由三个状态的马尔可夫模型描述：

状态S1：名词，S2：动词，S3：形容词

假设状态转移矩阵：

如果其中某一句话第一个词为名词，那么该句子中这三类词出现的顺序为0=“名动形名”的概率为：

系统初始化时可以定义一个初始状态的概率向量

隐马尔可夫链示意图：

2. 马尔可夫随机场 

马尔可夫随机场（Markov Random Field，MRF）是典型的马尔可夫网，著名的无向图模型

图模型表示：结点表示变量（集），边表示依赖关系。有一组势函数（Potential Functions)，亦称

“因子”(factor)，这是定义在变量子集上的非负实函数，主要用于定义概率分布函数

马尔可夫随机场（Markov Random Field，MRF）分布形式化：使用基于极大团的势函数（因子）

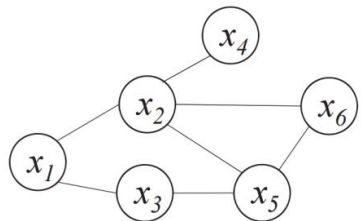
对于图中结点的一个子集，若其中任意两结点间都有边连接，则称该结点子集为一个“团”

（clique）。若一个团中加入另外任何一个结点都不再形成团，则称该团为“极大团”（maximal

clique)，图中 1, 2 , {2, 6} , {2, 5, 6}等为团，图中{2, 6}不是极大团，每个结点至少出现

在一个极大团中，多个变量之间的连续分布可基于团分解为多个因子的乘积。

基于极大团的势函数（因子）多个变量之间的连续分布可基于团分解为多个因子的乘积，每个因子

只与一个团相关。对于n个变量x={x1,x2,...xn}，所有团构成的集合为C，与团Q∈C对应的变量集合

记为XQ，则联合概率定义为：。

其中，是基于团Q对应的势函数，Z为概率的规范化因子，在实际应用中，Z往往很难精确计

算，但很多任务中，不需要对Z进行精确计算若变量问题较多，则团的数目过多，上式的乘积项过

多，会给计算带来负担，所以需要考虑极大团。

基于极大团的势函数：通过极大团构造势函数。若团Q不是一个极大团，则必然被一个极大团Q*包

含，这意味着变量的关系不仅体现在势函数中，还体现在*中联合概率分布可以使用极大

团定义假设所有极大团构成的集合为其中，Z*是规范化因子

。

基于极大团的势函数：联合概率分布可以使用极大团定义，假设所有极大团构成的集合为∗。

联合概率分布

马尔可夫随机场中的分离集：马尔可夫随机场中得到“ 条件独立性”。借助“分离”的概念，若从结点

集 中的结点到 中的结点都必须经过结点集 中的结点，则称结点集 ， 被结点集 分离，

称 为分离集（separating set）。

全局马尔可夫性：马尔可夫随机场中得到“条件独立性”，借助“分离”的概念，可以得到：全局马尔

可夫性（global Markov property）：在给定分离集的条件下， 两个变量子集条件独立。

图模型简化：

得到图模型的联合概率为：

全局马尔可夫性的验证：

条件概率：

验证：

马尔可夫随机场中的条件独立性：

由全局马尔可夫性可以导出：局部马尔可夫性(local Markov property):在给定邻接变量的情况下，

一个变量条件独立于其它所有变量令V为图的结点集，n(v)为结点v在图上的邻接节点，

成对马尔可夫性(pairwise Markov property)：在给定所有其它变量的情况下，两个非邻接变量条件

独立令V为图的结点集，边集为E，对图中的两个结点u,v,若不属于E，有

势函数的作用是定量刻画变量集XQ中变量的相关关系，应为非负函数，且在所偏好的变

量取值上有较大的函数值

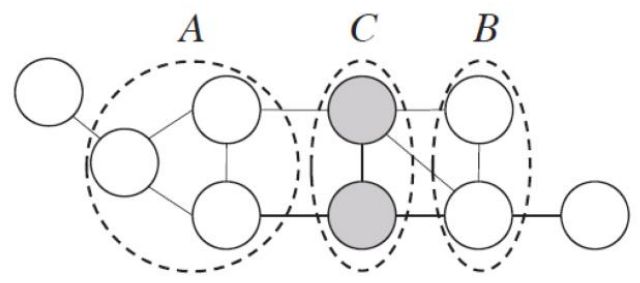
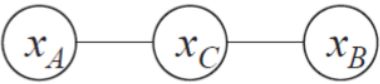
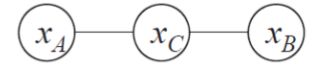
上图中，假定变量均为二值变量，定义势函数：

说明模型偏好xA与xc有相同的取值，xB与xc有不同的取值，换言xA与xc正相关，xB与xc负相关。

所以令xA与xc相同且xB与xc不同的变量值指派將有较高的联合慨率。

势函数的作用是定量刻画变量集xQ中变量的相关关系，应为非负函数，且在所偏好的变

量取值上有较大的函数值口为了满足非负性，指数函数常被用于定义势函数，即：

，其中，是一个定义在变量xQ上的实值函数，常见形式为：

，其中，是参数，上式第一项考虑每一对

结点的关系，第二项考虑单结点。

3. 条件随机场

条件随机场(Conditional Random Field，(CRF)是一种判别式无向图模型（可看作给定观测值的

MRF)，条件随机场对多个变量给定相应观测值后的条件概率进行建模，若令x={x1,X2,…,X}为观测

序列，y={y1,y2,,y}为对应的标记序列，CRF的目标是构建条件概率模型P(y|x)

标记变量y可以是结构型变量，它各个分量之间具有某种相关性。

自然语言处理的词性标注任务中，观测数据为语句（单词序列），标记为相应的词性序列，具有线

性序列结构在语法分析任务中，输出标记是语法树，具有树形结构

令G=(V,E)表示结点与标记变量y中元素一一对应的无向图。无向图中，yv表示与节点v对应的标记

变量，n(v)表示结点v的邻接结点，若图中的每个结点都满足马尔可夫性，

则(y,x)构成条件随机场。

CRF使用势函数和图结构上的团来定义P(y|x)。本章仅考虑链式条件随机场(chain-structured

CRF)，如下所亦：

链式条件随机场(chain-structured CRF)包含两种关于标记变量的团：相邻的标记变量，

单个标记变量；条件概率可被定义为：

是定义在观测序列的两个

相邻标记位置上的转移特征函数(transition feature function)，用于刻画相令邻标记变量之间的相关

关系以及观测序列对它们的影响，是定义在观测序列的标记位置i上的状态特征函数

(statusfeature function)，用于刻画观测序列对标记变量的影响，为参数，Z为规范化因子

特征函数通常是实值函数，以刻画数据的一些很可能成立或者期望成立的经验特性，以词性标注任

务为例：

采用特征函数：

表示第个观测值xi为单词'knock'时，相应的标记yi，yi+1很可能分别为[V]，[P]。

MRF 与CRF的对比：

MRF：使用团上的势函数定义概率，对联合概率建模

CRF：使用团上的势函数定义概率，有观测变量，对条件概率建模