详解二叉树经典基础算法

二叉树是我们平时学习当中一种常见的数据结构。在面试和学习当中我们难免会遇到一些跟二叉树有关的算法题。今天我为大家带来了几题经典的二叉树基础算法题，我们一起来看看吧！

目录

1.检查两棵树是否相同

①题目描述

 ②思路分析

③题解代码

2.另一颗树的子树

①题目描述

 ②思路分析

③题解代码

3.二叉树最大的深度

①题目描述

 ②思路分析

③题解代码

4.平衡二叉树

①题目描述

 ②思路分析

③题解代码

5.对称二叉树

①题目描述

 ②思路分析

③题解代码

6.最近公共祖先

①题目描述

②思路分析

③题解代码

7.根据前序和中序构建二叉树

①题目描述

 ②思路分析

③题解代码

---

1.检查两棵树是否相同

①题目描述

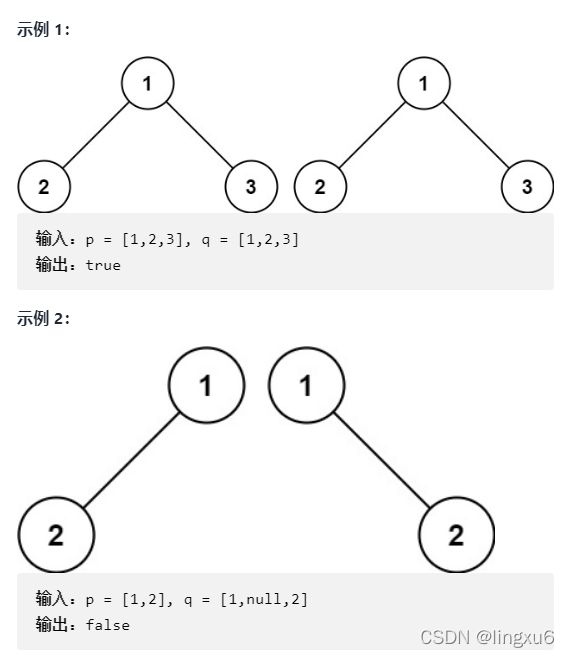
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。(来源：力扣（LeetCode）)

示例：

 ②思路分析

根据题目描述，我们在检验两颗二叉树是否相同时，可以先检验结构是否相同。那么基本可以分成一下几种情况：

一.两棵树的根节点有一颗为空，一颗不为空：false

二.两棵树都为空：true

三.两棵树都不为空：

1.值相同 ：检查子树

2.值不同：false

③题解代码

    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p != null && q == null) {
            return false;
        } else if(p == null && q != null) {
            return false;
        }else if(p == null && q == null) {
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }

2.另一颗树的子树

①题目描述

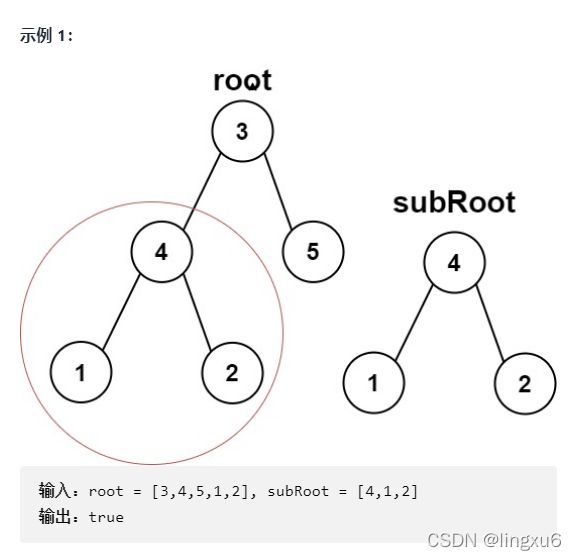
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。(来源：力扣（LeetCode）)
 

示例：

 

 ②思路分析

根据题目描述，我们在检验subRoot是否为root子树时可以分为以下几步：

一.检验两棵树是否相同（代码为第一题）

1.相同：true

2.不同：

①判断root是否为空（如果不判断，下面引用其左右子树可能会空指针异常）

②递归自身左子树和右子树

③题解代码

    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(isSametree(root, subRoot)) {
            return true;
        } else if(root == null) {
            return false;
        }
        return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }
    public static boolean isSametree(TreeNode p, TreeNode q) {
        if(p == null && q != null || p != null && q == null) {
            return false;
        } else if(p == null && q == null) {
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSametree(p.left, q.left) && isSametree(p.right, q.right);
    }

3.二叉树最大的深度

①题目描述

给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。说明: 叶子节点是指没有子节点的节点。(来源：力扣（LeetCode）)

示例：

              

 

 ②思路分析

根据题目描述，我们第一个联想到的应当是层序遍历，统计其层数即可，但是层序在这里显得有些大才小用了。我们可以这样想：一棵树向左遍历如果遍历到空节点就返回0，同时向右遍历，遇到空节点也返回0；那么当叶子节点向下遍历时左右皆为空，因此该子树的深度应当是只有叶子节点本身。另一种情况：如果左右有一个不为0或者都不为0，那么我们就应当取其最大值。我们来整理一下思路：

一.检验root是否为空

1.空：返回0

2.不空：递归计算左右子树的深度

①返回左右子树最大深度再加上当前根节点本身

③题解代码

    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left, right) + 1;
    }

4.平衡二叉树

①题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。(来源：力扣（LeetCode）)

示例：

 

 ②思路分析

我们首先检查根节点是否为空，如果根节点不为空我们求左右子树是否满足平衡二叉树的定义。注意：如果一棵树是平衡二叉树，其子树一定是平衡二叉树。那么知道这个道理以后，我们可以递归检查子树，如果不满足就代表整棵树都不是平衡二叉树。

一.检查root是否为空

空:返回true;

不空：

1.递归计算左右子树深度

2.判断左右子树是否都大于0，判断左右子树深度差值是否小于2

小于2：

①.返回当前子树深度

大于等于2：

①返回-1

如果最终返回值为正数，代表是平衡二叉树

③题解代码

    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        return high(root) >= 0;
    }
    public int high(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int left = high(root.left);
        int right = high(root.right);
        if(left >= 0 && right >= 0 && Math.abs(left - right) < 2) {
            return Math.max(left, right) + 1;
        } else {
            return -1;
        }
    }

5.对称二叉树

①题目描述

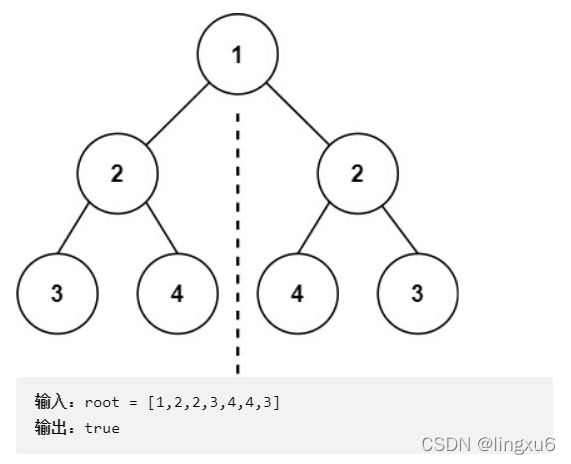
给你一个二叉树的根节点 root ， 检查它是否轴对称。(来源：力扣（LeetCode）)

示例：

 

 ②思路分析

此题较为简单，只需要递归左右子树首先判断空的情况，再判断值是否相同。如果发现不满足直接返回false即可。

③题解代码

    public boolean isSymmetric(TreeNode root) {
        if(root == null) {
            return true;
        }
        return isS(root.left, root.right);
    }
    public static boolean isS(TreeNode r1, TreeNode r2) {
        if(r1 == null && r2 != null || r1 != null && r2 == null) {
            return false;
        }
        if(r1 == null && r2 == null) {
            return true;
        }
        if(r1.val != r2.val) {
            return false;
        }
        return isS(r1.left, r2.right) && isS(r1.right, r2.left);
    }

6.最近公共祖先

①题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大，一个节点也可以是它自己的祖先。(来源：力扣（LeetCode）)

示例：

 

②思路分析

我们首先判断当前根节点是否为空，如果根节点为空那么我们直接返回空节点表示找不到祖先节点。如果当前根节点不为空，我们判断根节点是否跟某一个我们要找的节点相同。我们可以将根节点的情况分为三类：1.p，q两个节点分布在某个节点的左右子树，那么该节点就是他们的最近公共祖先。2.p是q的公共祖先。3.q是p的公共祖先。

一.判断root是否为空：

1.空：返回null

2.不空：

①判断是否等于p或q其中一个，如果相等直接返回当前节点

②不相等，开始左右遍历子树，判断p和q在哪一侧；

③根据返回值，如果左右返回都为空，则代表不在这棵树，我们也返回空。左右有一个不为空，返回不为空的值。如果左右都不为空，代表当前节点就是祖先节点，直接返回。

③题解代码

     public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) {
            return null;
        }
        if(root == p || root == q) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null && right != null) {
            return right;
        } else if(left != null && right == null) {
            return left;
        } else if(left == null && right == null) {
            return null;
        }
        return root;
    }

此外，还有一种解题思路：找出该树到达p和q的路径，然后转化为链表求公共交点；

代码：

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q) {
            return root;
        }
        Stack sta1 = new Stack<>();
        Stack sta2 = new Stack<>();
        findPath(root, p, sta1);
        findPath(root, q, sta2);
        int size = Math.abs(sta1.size() - sta2.size());
        if(sta1.size() > sta2.size()) {
            for(int i = 0; i < size; i++) {
                sta1.pop();
            }
        } else {
            for(int i = 0; i < size; i++) {
                sta2.pop();
            }
        }
        TreeNode ance = null;
        while(sta1.size() != 0) {
            TreeNode t1 = sta1.pop();
            TreeNode t2 = sta2.pop();
            if(t1 == t2) {
                ance = t1;
                break;
            }
        }
        return ance;
    }
    public static boolean findPath(TreeNode root, TreeNode tar, Stack sta) {
        if(root == null) {
            return false;
        }
        if(root == tar) {
            sta.push(root);
            return true;
        }
        sta.push(root);
        boolean bool = findPath(root.left, tar, sta);
        if(bool) {
            return true;
        } else {
            bool = findPath(root.right, tar, sta);
        }
        if(bool) {
            return true;
        }
        sta.pop();
        return false;
    }

7.根据前序和中序构建二叉树

①题目描述

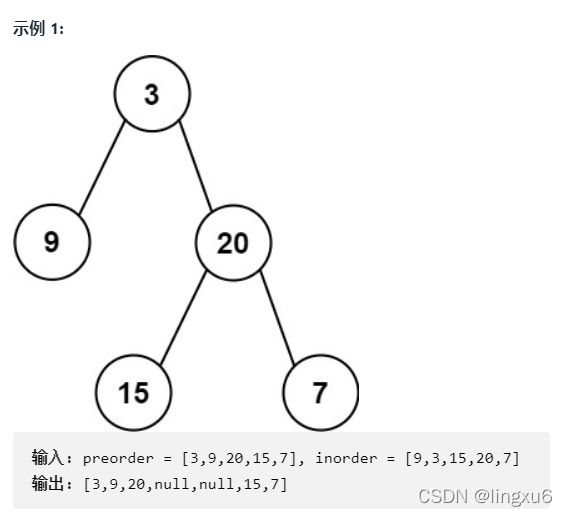
给定两个整数数组 pre 和 in ，其中 pre 是二叉树的先序遍历， in是同一棵树的中序遍历，请构造二叉树并返回其根节点。(来源：力扣（LeetCode）)

示例：

 ②思路分析

我们首先要了解两件事：1.前序遍历是所有的根的集合 2. 在中序遍历中找到某个指定的根，那么左边是他的左子树的中序遍历，右边是右树的中序遍历。根据以上结论：我们可以定义两个引用，第一个从前序数组0下标开始往后走，第二个在中序序列中找到第一个引用的值，即找到根的值。那么中序序列就被分成了左右两块，分别对用刚刚根的左右子树。以此类推进行递归就可以了。

③题解代码

    int x = 0;
    public TreeNode buildTree(int[] pre, int[] in) {
        int left = 0;
        int right = in.length - 1;
        int val = pre[x];
        x++;
        int pivot = find(in, val, left, right);
        if(pivot == -1) {
            return null;
        }
        TreeNode cur = new TreeNode(val);
        cur.left = build(pre, in, left, pivot - 1);
        cur.right = build(pre, in, pivot + 1, right);
        return cur;
    }
    public TreeNode build(int[] pre, int[] in, int left, int right) {
        if(left > right) {
            return null;
        }
        int val = pre[x];
        x++;
        int pivot = find(in, val, left, right);
        if(pivot == -1) {
            return null;
        }
        TreeNode cur = new TreeNode(val);
        cur.left = build(pre, in, left, pivot - 1);
        cur.right = build(pre, in, pivot + 1, right);
        return cur;
    }
    public int find(int[] in, int val, int left, int right) {
        for(int i = left; i <= right; i++) {
            if(in[i] == val) {
                return i;
            }
        }
        return -1;
    }

以上就是今天的全部内容了，创作不易，喜欢的话请点个赞吧！