力扣二叉树相关面试题（5道）

第一题二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

输入：root = [1,null,2,3]
输出：[1,2,3]

递归就完事了。前序中序后序都一样遍历就行了。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List <Integer> list=new ArrayList<>();
        if(root==null){
            return list;
        }
        list.add(root.val);
        List<Integer>lefttree =preorderTraversal(root.left);
       list.addAll(lefttree);
         List<Integer>righttree =preorderTraversal(root.right);
         list.addAll(righttree);        
return list;
    }
}

有人就要问了为啥这个代码不能直接
list.add(root.val);
preorderTraversal(root.right);
preorderTraversal(root.right);
这里要和大家解释一下我们所用的list是一个局部变量。关键就是理解名字都是 list，但不是同一个变量，而是每次方法执行，都有一个 list。递归返回时需要一个list来接收，为什么是addAll因为你递归不可能只递归一次。

第二题检查两颗树是否相同

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

输入：p = [1,2,3], q = [1,2,3] 输出：true

分析我们要先判断如果都为空，或者一个为空另一个不为空的情况。然后如果相同了，我们就要看树的左右结点是否相同。按这个思想递归这来。

class Solution {
    
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p!=null&&q==null||p==null&&q!=null){
           return false;
       }
         if(p==null && q==null){
        return true;
       }
       if(p.val!=q.val){
          return  false;
       }
       return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
      
    }
}

第三题另一颗树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/subtree-of-another-tree

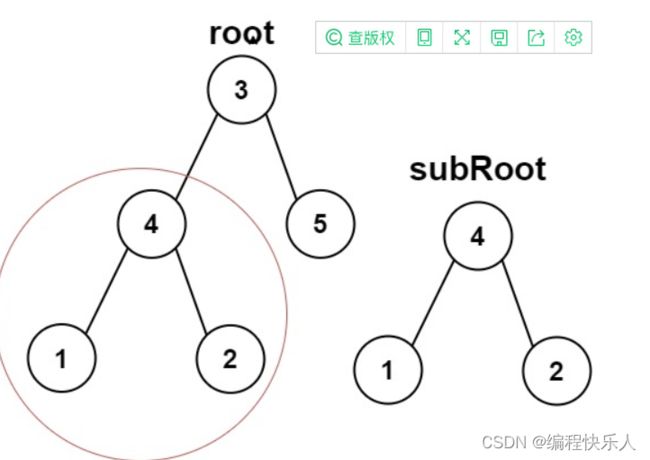
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true
思路和上道题一样，就是这道题我们需要递归一下。如果这个结点的结构和该结构不一样，我们就去遍历该结构的左右结构。

class Solution {
    public boolean isSameTree(TreeNode root,TreeNode subRoot){
        if(root==null&&subRoot!=null||root!=null&&subRoot==null){
            return false;
    }
    if(root==null&&subRoot==null){
        return true;
    }
    if(root.val != subRoot.val){
        return false;
    }
    return isSameTree(root.left,subRoot.left)&&isSameTree(root.right,subRoot.right);
    }
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root==null||subRoot==null){
            return false;
        }
        if(isSameTree(root,subRoot)){
            return true;
        }
           if(isSubtree(root.left,subRoot))return true;
           if (isSubtree(root.right,subRoot))return true;
            return false;
        }
}

第四题二叉树最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

   3
 /  \
9  20
/   \
15   7
返回它的最大深度 3 。

思路
拿一个头节点如果为空就没有深度，如果有就为1，然后看子节点如果为空就深度为1，如果不为空就+1.

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
         int right=maxDepth(root.right);
        int  left=maxDepth(root.left);
        return left>right?left+1:right+1;
    }
}

第五题判断一颗二叉树是否是平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

输入：root = [3,9,20,null,null,15,7]
输出：true
题解：这道题我们把他分解了之后会很容易，我们先判断树是不是空的然后判断这个树是不是平衡的（可以用四题的公式然后求出差值为一的树结点），然后判断子树左右是不是也是平衡的。

class Solution {
     public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        int right=maxDepth(root.right);
        int  left=maxDepth(root.left);
        return left>right?left+1:right+1;
    }
    public boolean isBalanced(TreeNode root) {
        if(root==null){
            return true;
        }
        int leftH= maxDepth(root.left);
       int rightH=maxDepth(root.right);
       return Math.abs(leftH-rightH)<=1&&isBalanced(root.left)&&isBalanced(root.right);       
    }
}