双非本科准备秋招（18.1）—— 力扣二叉树

1、404. 左叶子之和

方法一：

        可以在父节点判断一下，如果左子树不为null，并且左子树没有左右子树，说明这是个左叶子节点。

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null) return 0;

        int LV = sumOfLeftLeaves(root.left);
        int RV = sumOfLeftLeaves(root.right);

        int t = 0;
        if (root.left != null && root.left.left == null && root.left.right == null) { 
            t = root.left.val;
        }

        return t+LV+RV;
    }
}

 方法二，找bug：

        一开始我用的递归，用布尔值传值，于是我写了如下代码。

class Solution {
    static int ans = 0;
    public int sumOfLeftLeaves(TreeNode root) {
        preOrder(root, false);

        return ans;
    }
    static void preOrder(TreeNode root, boolean isLeft){
        if(root == null) return;
        if(isLeft && root.left == null && root.right == null){
            ans += root.val;
            return;
        }
        preOrder(root.left, true);
        preOrder(root.right, false);
    }
}

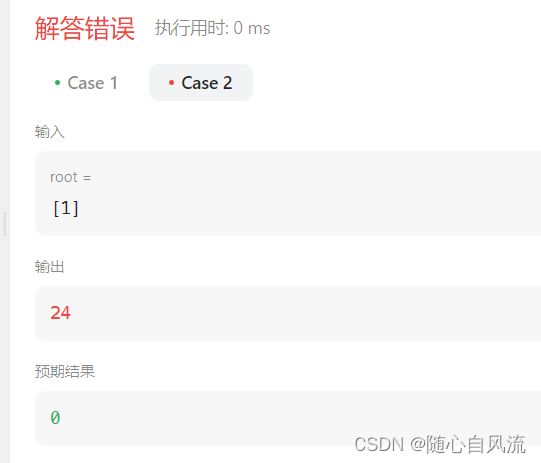
        这个测试用例竟然会输出24。

        想了一天，晚上突然明白了，测试用例1答案是24，测试用例2答案应该是0，但是为什么是24呢？因为测试用例2答案在第一个基础上，也就是24+0 = 24

        而我的ans变量是static的，也就是所有实例共享的，把代码改成下面这样就过了。

class Solution {
    int ans = 0;
    public int sumOfLeftLeaves(TreeNode root) {
        preOrder(root, false);

        return ans;
    }
    void preOrder(TreeNode root, boolean isLeft){
        if(root == null) return;
        if(isLeft && root.left == null && root.right == null){
            ans += root.val;
            return;
        }
        preOrder(root.left, true);
        preOrder(root.right, false);
    }
}

        

2、513. 找树左下角的值

        这个题应该挺好想的，左下角是最底层，最左边的值，用层序遍历就很好实现，遍历到最后一层记录第一个值就是答案。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        //层序遍历 最后一层 第一个节点
        LinkedList q = new LinkedList<>();
        int ans = 0;
        if(root == null) return 0;
        q.offer(root);
        while(!q.isEmpty()){
            int len = q.size();
            for(int i = 0; i < len; i++){
                TreeNode t = q.poll();
                if(i == 0) ans = t.val;
                if(t.left != null){
                    q.offer(t.left);
                }
                if(t.right != null){
                    q.offer(t.right);
                }
            }
        }
        return ans;
    }
}

3、112. 路径总和

        跟昨天的输出路径题一个套路（257. 二叉树的所有路径），核心还是判断是不是叶子节点，当左右子树都为null并且传的值等于target的时候说明找到了，为了保证不出现空指针异常，每次递归都要判断一下。

class Solution {
    boolean f = false;
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null) return f;
        preOrder(root, targetSum, 0);
        return f;
    }
    void preOrder(TreeNode root, int target, int n){
        if(f) return;

        n += root.val;
        if(root.left == null && root.right == null && n == target){
            f = true;
            return;
        }

        if(root != null && root.left != null) preOrder(root.left, target, n);
        if(root != null && root.right != null) preOrder(root.right, target, n);
    }
}

4、654. 最大二叉树

        跟昨天做的根据前序中序构造树一个思路，代码都很像，for循环找到最大值，然后根据最大值位置划分左右子树，递归地遍历左右子树，左子树范围0——index，右子树范围index+1——length。

        但是要注意判断一下index是否是边界，也就是为0或length-1的时候，左子树或右子树直接就是null了。

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        int r = -1, index = 0;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] > r){
                r = nums[i];
                index = i;
            }
        }
        TreeNode root = new TreeNode(r);
        if(index == 0) root.left = null; 
        else root.left = constructMaximumBinaryTree(Arrays.copyOfRange(nums, 0, index));
        if(index == nums.length-1) root.right = null;
        else root.right = constructMaximumBinaryTree(Arrays.copyOfRange(nums, index+1, nums.length));
        return root;
    }
}

5、617. 合并二叉树

        核心在于如何同步遍历两个二叉树。

        每次把结果都加到root1这棵树上就好，节省空间。

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null) return root2;
        if(root2 == null) return root1;

        root1.val += root2.val;
        root1.left = mergeTrees(root1.left, root2.left);
        root1.right = mergeTrees(root1.right, root2.right);
        
        return root1;
    }
}