插入排序、选择排序和冒泡排序详解
排序对于任何一个程序员来说可能都不陌生,在我们日常的开发中多多少少都会涉及到排序的场景,如按照订单交易时间排序,按照金额排序等等。很多语言都内置了相应的排序函数,而且讲起排序算法时都可以列出一大堆,此文初步探索下插入排序,选择排序和冒泡排序。
此处先说明下排序算法的稳定性:
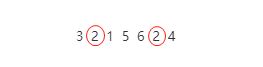
稳定性,这个概念是说,如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变,如下待排序的序列。
图中框住的两个元素2,排序后相对位置不变,前面的2 还是在前面,后面的2还是相对在后面。其实你也许有疑问,这两个2谁在前面谁在后面貌似对结果都没有影响,貌似都没有差别。似乎这个稳定性没多大意义。其实不然,我们这里是以整型数据类进行举例,现实中我们待排序的数据往往是复杂的对象,而不是简单整型。比如有如下商品,商品有两个属性,金额和浏览量
public class Goods {
//商品名称
public String name;
//商品金额
public int amount;
//商品浏览量
public int view;
}比如说,我们现在要给商品进行排序,我们希望按照浏览量进行排序,对于浏览量相同的商品,我们希望按照金额从低到高进行排序,对于这样一个排序需求我们怎么做呢?
最先想到的方法是:我们先按照浏览量对商品数据进行排序,然后,再遍历排序之后的商品数据,对于每个浏览量相同的小区间再按照金额排序。这种排序思路理解起来不难,但是实现起来会很复杂。
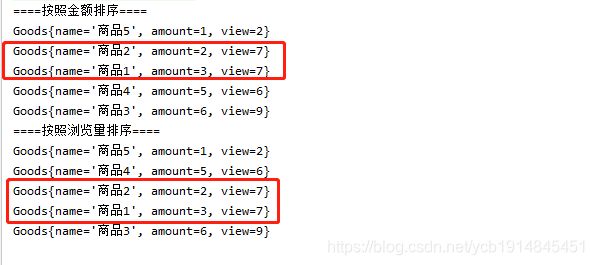
借助稳定排序算法,这个问题可以非常简洁地解决。解决思路是这样的:我们先按照金额给商品排序,注意是按照金额,不是浏览量。排序完成之后,我们用稳定排序算法,按照商品浏览量重新排序。两遍排序之后,我们得到的商品数据就是按照浏览量从小到大排序,浏览量相同的商品按照金额从小到大进行排序。为什么呢?
稳定排序算法可以保持浏览量相同的两个对象,在排序之后的前后顺序不变。第一次排序之后,所有的商品按照金额从小到大排序了。在第二次排序中,我们用的是稳定的排序算法,所以经过第二次排序之后,相同浏览量的商品仍然保持金额从小到大。如下所示
有序度、逆序度和满有序度介绍:(假设要求元素升序排列)
1. 概念:
满有序度:所有排列的个数
有序度:满足排序规则的排列个数
逆序度:未满足排序规则的排列个数
排序的过程,即为有序度递增的过程。当有序度等于满有序度时,数组有序。
2. 公式:
满 有 序 度 = ( n − 1 ) ∗ n / 2
逆 序 度 = 满 有 序 度 − 有 序 度
3. 示例:
对于集合(3, 4, 2, 1)
满有序度=(n−1)∗n/2=(4−1)∗4/2=6。即(3,4),(3,2),(3,1),(4,2),(4,1),(2,1)
有序度=1。即(3,4)
逆有序度=6−1。即(3,2),(3,1),(4,2),(4,1),(2,1)
其实我们的排序过程就是让逆序度减少,让有序度增加,直到有序度等于满有序度时,逆序度为0,序列有序。其实元素交换的次数就等于逆序度。
接下来我们来看下几种排序算法:
冒泡排序
如下图,所以从第一个元素开始,通过不断的交换,经过第一次冒泡,最大值被排序到最后。
再从剩下的元素中进行同样的操作,如下图,剩下的最大的值被冒泡到倒数第二位。
接下来再从剩下的元素中不断的进行上面操作,直到序列有序,经过上面分析代码如下。
public static void bubbleSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = nums.length - 1; i >= 0; i--) {
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j + 1];
nums[j + 1] = nums[j];
nums[j] = temp;
}
}
}
}时间复杂度为O(![]() ),空间复杂度为O(1),原地排序算法,我们可以分析出冒泡排序是稳定的排序算法。
),空间复杂度为O(1),原地排序算法,我们可以分析出冒泡排序是稳定的排序算法。
其实上述代码还可以进行优化,比如下图
此时的状态我们已经把后面的两个元素有序,此时再进行冒泡时因为元素已经有序,所以不需要进行交换,当然后续也不需要再进行冒泡,所以我们可以进行适当的优化,增加一个标志变量,当某次冒泡时没发生元素交换,表明已经有序,不需要再进行后续的操作。代码如下:
public static void bubbleSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = nums.length - 1; i >= 0; i--) {
//增加一个标志变量
boolean flag = false;
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j + 1];
nums[j + 1] = nums[j];
nums[j] = temp;
//表明此次有进行元素交换
flag = true;
}
}
//当某一次没有进行元素交换时不需要再执行后续的操作
if (flag == false) {
break;
}
}
}插入排序
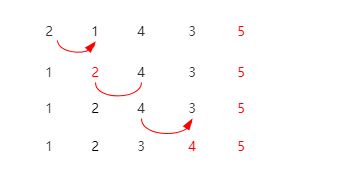
也许大家都打过扑克牌,我们斗地主时每抓起一张牌就会把这一张牌插入到手上已排序的牌的合适位置,其实插入排序和这个类似的。我们可以看下以下数组的数据。对于已排序的数组1 3 5 ,插入元素2时变化情况。扑克牌这个是类似于一个动态排序的过程。
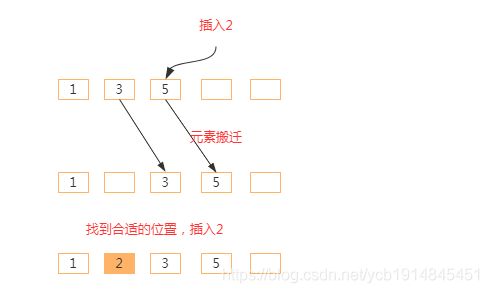
其实插入排序我们也可以使用相同的思路。我们可以把待排序的数组分为已排序区间和未排序区间,只有一个元素时一定是有序的,我们可以把第一个元素组成的区间初步定义为已排序区间,2 - N元素组成的区间定义为未排序区间。如下所示。
然后每一次我们从未排序区间依次取出一个元素插入到已排序区间,扩大已排序区间,缩小未排序区间,直到未排序区间缩小为0,已排序区间扩大为整个数组区间。如下,如果我们取出元素3后的情况。此时已排序区间扩大一个元素,未排序区间缩小一个元素。依次类推。
经过上面分析代码如下。
public static void insertSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
for (int i = 1; i < nums.length; ++i) {
//从未排序区间取出的待插入到已排序区间的元素
int value = nums[i];
int j = i - 1;
//为本次待插入的元素找到合适的插入位置
for (; j >= 0; --j) {
if (nums[j] > value) {
nums[j + 1] = nums[j];
} else {
break;
}
}
//至于此处为什么是j + 1,因为我们初始时设置的是j = i -1
nums[j + 1] = value;
}
}时间复杂度为O(![]() ),空间复杂度为O(1),原地排序算法,我们可以分析出插入排序是稳定的排序算法。
),空间复杂度为O(1),原地排序算法,我们可以分析出插入排序是稳定的排序算法。
选择排序
如果有N个人排成一对,现在需要把这些人按照身高从低到高进行排序,如果按照选择排序该怎么进行?
我们首先从N个人里面选择身高最低的一个人,把这个人放在第一位,再从接下来的2 - N个人里面选择身高最低的一个放置于第二个位置,直到N个人按照从低到高排序。如下图所示,知道所有的元素都已排序
经过上面分析,代码如下:
public static void selectionSort(int[] nums) {
if (nums == null || nums.length == 0) return;
for (int i = 0; i < nums.length; ++i) {
//找到最小的元素索引
int minIndex = i;
for (int j = i + 1; j < nums.length; ++j) {
if (nums[minIndex] > nums[j]) {
minIndex = j;
}
}
//元素交换
if (minIndex != i) {
int temp = nums[i];
nums[i] = nums[minIndex];
nums[minIndex] = temp;
}
}
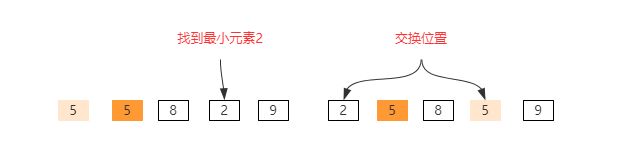
}时间复杂度为O(![]() ),空间复杂度为O(1),原地排序算法,但是选择排序不是稳定的排序算法,交换时对于值相同的元素会导致元素的前后位置发生变化。比如如下图,经过第一轮选择排序,会导致两个元素5的前后顺序发生变化。
),空间复杂度为O(1),原地排序算法,但是选择排序不是稳定的排序算法,交换时对于值相同的元素会导致元素的前后位置发生变化。比如如下图,经过第一轮选择排序,会导致两个元素5的前后顺序发生变化。
冒泡排序和插入排序的时间复杂度都是 O(N^2),都是原地排序算法,为什么插入排序要比冒泡排序更受欢迎呢?
我们前面分析冒泡排序和插入排序的时候讲到,冒泡排序不管怎么优化,元素交换的次数是一个固定值,是原始数据的逆序度。插入排序是同样的,不管怎么优化,元素移动的次数也等于原始数据的逆序度。但是,从代码实现上来看,冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要 3 个赋值操作,而插入排序只需要 1 个。
我们来看这段操作:
//冒泡排序的数据交换操作
if (nums[j] > nums[j + 1]) {
int temp = nums[j + 1];
nums[j + 1] = nums[j];
nums[j] = temp;
//表明此次有进行元素交换
flag = true;
}
//插入排序的数据移动操作
if (nums[j] > value) {
nums[j + 1] = nums[j];
} else {
break;
}
我们把执行一个赋值语句的时间粗略地计为单位时间(unit_time),然后分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序,需要 K 次交换操作,每次需要 3 个赋值语句,所以交换操作总耗时就是 3*K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。但这是理论的分析,实际上应该达不到3倍。