C语言学习|原码反码补码和位的操作符

目录

原码反码和补码 

原码(true code)

反码(complemental code)

补码(ones-complement code)

溢出的处理

位运算符

移位操作符 << >>

<< 左移

>> 右移

按位操作符 & | ^

& 按位与

| 按位或

^ 按位异

~ 按位反

 

移位操作符的代码实例

求对应值的补码(二进制)

---

原码反码和补码 

计算机内存储存变量都是通过二进制储存，计算机只看得懂二进制，0(代表低电流)，1(代表高电流)，通过二进制描述正负数，便诞生了原码的概念；如何实现加减法，为了通过加法实现减法，反码便出现了；针对反码的一些不足，对进行反码改进，补码便诞生了。计算机内存储存变量和进行变量计算都是通过补码，因此原码，反码和补码十分重要。

原码(true code)

原码(true code)是计算机对二进制数定点表示的一种方法，其中在二进制的前面加了一位符号位，0表示整数，1表示负数，0可以用+0和-0表示。

十进制	原码(6个进制位表示)
10	001010
3	000011
0	000000/100000
-3	100011
-10	101010

利用原码可以进行加法运算，但不能通过加法来实现减法运算，用原码进行减法运算需要添加减号模块，实现麻烦。

3+10 = 000011+001010 = 001101 = 13

10-3 = 10 + (-3) = 001010 + 100011 = 101101 = -13 ×

反码(complemental code)

反码是对二进制数表示的方法，它是为了通过加法来实现减法运算而诞生的。正数的反码是它本身，而负数的反码是除了符号位以外，二进制位的0变成1,1变成0得到反码。

十进制数	原码	反码
7	000111	000111
5	000011	000011
0	000000/100000	000000/111111
-3	100011	111100
-5	100101	111010

通过反码，就可以进行减法运算，但不足的是0也有两个对应的反码，而且如果有溢出，需要做+1处理。

22 - 5 = 22+(-5)=010110 + 111010 = 1 010000 = 010000 + 000001 = 010001= 17

其中，红色表示溢出，黄色是溢出的处理，如果二进制有溢出，需要加1，然后舍掉溢出的位置，这样便可以实现减法运算。

反码解决了减法的运算，但是0有两个对应的反码，而且如果溢出时需要处理，可不可以优化呢？

补码(ones-complement code)

补码是反码的延伸，它同样是表示二进制数的一种方法，正数的补码是自己本身，而负数的补码是反码+1，补码就像是反码上加了个补丁，修补了反码的缺点。同时规定0的补码为000000(全0)。

通过补码的补充，0有了唯一对应的二进制，而且不仅可以处理减法运算，也能更方便地处理溢出操作。

22 - 5 = 22+(-5)=010110 + 111011 = 1 010001 = 010001 = 17

其中，红色是溢出位，运用补码进行运算，直接舍弃溢出的数字，保留其余二进制，就是结果。

补码也同时规定 -2^6 = -64的补码为100000，没有六位二进制的原码和反码。补码相对于反码不仅优化了溢出的操作，更解决了0的对应问题，0在反码中只有唯一的二进制与其对应。相比较而言，反码代表的数字比原码和反码都多1个,表示的范围也更大。在计算机系统中，数值一律用补码计算和表示。

(n位二进制)	原码	反码	补码
可表示的个数	2^n-1	2^n-1	2^n
表示范围	-(2^n-1)~(2^n-1)	-(2^n-1)~(2^n-1)	-2^n~(2^n-1)

C语言中，int类型的变量大小为4个字节，32个比特位，也就是用32位二进制储存，其中第一位是符号位，则int类型的范围是 -(2^31) ~ (2^31-1)

溢出的处理

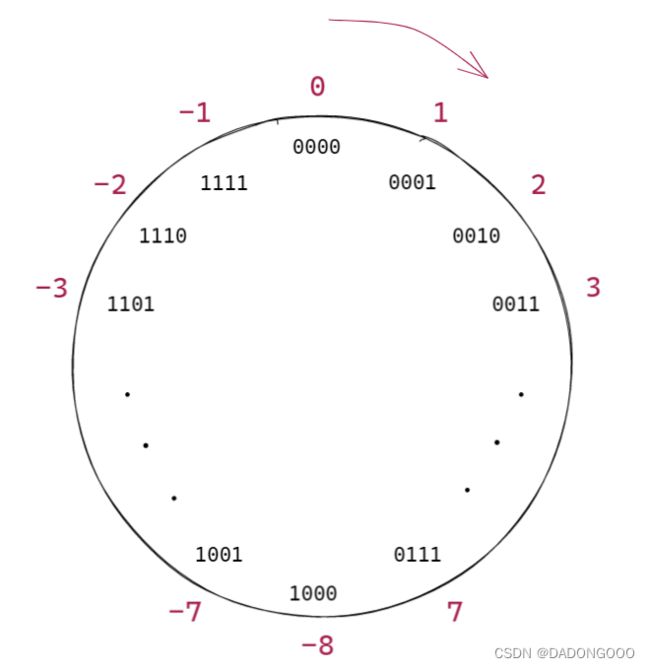
如果表示的数字超过了范围怎么办，计算机对于溢出的处理类似时钟的转动，如图所示

 对于四位二进制，可表示的范围是-8~7，如果超出了7，则会沿着时钟继续前进。如果超过了1个，则前进1个单位，也就是-8，然后继续转动，加是向右转动，减是向左转动，时钟很好的解决了范围的边界问题。我们在C语言经常看到，当数大到一定程度的时候变成了负数，也是这样的原理。

以上就是计算机关于位的处理，接下来我们来看C语言中的位操作符

位运算符

位运算符均是对补码进行操作，因为计算机对数值的存储就是通过补码存储，而且位运算符只能对整数进行处理，均是双目操作符，即需要两个对象。在C语言中，位运算符主要有 << 左移， >> 右移，^ 异或和~取反操作符，。假设有整数变量 int a = 10;

移位操作符 << >>

<< 左移

a << 2,对a的补码左移两位，<< 对变量的补码进行左移，新上来的位补0，左边溢出的位直接舍掉。a的结果就是a*(2^2)，也就是40，左移n位就是乘以2的n次方。

int main()
{
	int a = 10;
	int b = 0;
	b = a << 2; //a<<2,但不改变原来a的值
	printf("a = %d\n", a); // a = 10
	printf("b = %d", b); // b = 40
	return 0;
}

>> 右移

a>>1,将a的补码向右移动1位，如果是正数，则左边补0，负数左边补1,右边溢出的位直接舍弃。>> 是右移操作符，对变量补码进行右移操作。

int main()
{
	int a = -3;
	int b = 0;
	b = a >> 2; //对a的补码向右移动2位
	printf("a = %d\n", a); //a = -3
	printf("b = %d", b); //b = -1
	return 0;
}

按位操作符 & | ^

& 按位与

c = a & b ，将a与b的补码每一位进行比照，如果a和b所对应位都是1则是1，否则是0，传给c的对应二进制位。

int main()
{
	int a = -6;
	int b = -2;
	int c = 0;
	c = a & b; // c的补码(8位) 11111010，转换为原码，对补码取反+1，即10000110(-6)
	printf("c = %d\n", c); //c = -6
	return 0;
}

| 按位或

c = a & b ，将a与b的补码每一位进行比照，如果a和b所对应位其中一个是1则是1，否则是0传给c的对应二进制位。

int main()
{
	int a = -6;
	int b = -2;
	int c = 0;
	c = a | b; // c的补码(8位) 11111110，转换为原码，对补码取反+1，即11111110(-2)
	printf("c = %d\n", c); //c = -2
	return 0;
}

^ 按位异

c = a ^ b ，将a与b的补码每一位进行比照，如果a和b所对应位不同则是1，相同是0，传给c的对应二进制位。

int main()
{
	int a = 7;
	int b = 13;
	int c = 0;
	c = a ^ b; 
	printf("c = %d\n", c); //c = 10
	return 0;
}

其中，^操作符有以下的性质
a^a  = 0  a异或自身得到的结果是0
a^0 = a   a异或0得到的是自身a
a^b^c = a^c^b 异或操作符支持交换律和结合，由此 如果 a^b^a = b  a^b^b = a

~ 按位反

~a，对a的补码取反，是1则是0，0则是1,，是单目操作符。对一个数的补码取反。

int main()
{
	int a = 10;
	printf("~a = %d", ~a); //~a = -11
	return 0;
}

移位操作符的代码实例

求对应值的补码(二进制)

右移实现

void RBinnary(int num)
{
	int i = 0;
	for (i = 31; i >=0; i--)
	{
		printf("%d", (num >> i) & (1));
	}
}

int main()
{
	int a = -2;
	RBinnary(a);
	return 0;
}

左移实现

void LBinnary(int num)
{
	int i = 0;
	for (i = 0; i <32; i++)
	{
		int is_one = (num << i) & (1 << 31);
		if (is_one)
			printf("1");
		else
			printf("0");
	}
}

int main()
{
	int a = -2;
	LBinnary(a);
	return 0;
}