图形系统开发实战课程:进阶篇(上)——1.基础知识
图形开发学院|GraphAnyWhere
- 课程名称:图形系统开发实战课程:进阶篇(上)
- 课程章节:“基础知识”
- 原文地址:https://graphanywhere.com/graph/advanced/2-1.html
第一章 基础知识
\quad 在学习开发前端图形组件之前,我们先来掌握一些基础知识。
1 HTML5和Canvas
\quad
(1)
\quad 在Html中可通过插入canvas标签,并指定canvas的宽度和高度即可开始图形渲染。canvas的默认大小为300像素×150像素(宽×高,像素的单位是px),需注意的是在设置canvas的宽和高时直接指定数字即可,不能使用px后缀,也不能通过样式style指定画布的宽高。
<canvas id="mycanvas" width="800" height="600">canvas>
(2) Canvas画布
\quad 在网页插入
以下代码示例可得到画布对象。
let canvas = document.getElementById("mycanvas");
(3) 渲染上下文
\quad 在Canvas中,渲染上下文是一个非常重要的概念。一切图形绘制均是在此上下文对象上进行。画布除了可提供二维上下文对象,还可提供实现三阶渲染效果的WEBGL上下文对象。
\quad 本系列课程讲述的内容均是使用该二维渲染上下文对象实现的图形渲染。简称渲染上下文,后续内容除了特别说明之外,渲染上下文均是指二维渲染上下文。
\quad canvas通过getContext()方法得到上下文对象,getContext()接受一个参数,即上下文的类型。对于2D图像而言,使用参数’2d’得到该对象。二维渲染上下文对象的官方术语为:CanvasRenderingContext2D。
let canvas = document.getElementById("tutorial");
let ctx = canvas.getContext("2d");
\quad 渲染上下文提供了许多api用于图形绘制,同时也提供了一些属性用于指定图示绘制的样式,包括颜色、线宽、字体名称和大小等等。下面这个示例将在画布中绘制一个矩形,其代码如下:
// 1、从Html中获取画布对象
let canvas = document.getElementById("tutorial");
// 2、从画布中获取渲染上下文对象
let ctx = canvas.getContext("2d");
// 3、绘制矩形
ctx.strokeRect(50, 50, 200, 120);
2 JavaScript
\quad JavaScript是Web前端开发的主要语言,被设计用来使网页具有交互性。ES6(ECMAScript 6)是JavaScript目前最广泛使用的版本,于2015年发布。它引入了许多新的特性,使JavaScript编写更加方便和高效。
\quad anyGraph采用javascript作为开发语言,使用了ES6的一些特性,例如模块化、类、Promise对象等。
(1) 模块化编程
\quad JavaScript模块化编程是一种将代码划分为独立、可重用的模块的方式,以便更好地组织、维护和复用代码。通过模块化编程,可以将代码拆分为多个文件,每个文件负责实现特定的功能或逻辑,并且可以通过导入和导出机制来组合和共享代码。
\quad JavaScript模块化编程支持多种模块化方案,如CommonJS、ES6模块等,其中ES6模块是最新的标准。
CommonJS
\quad CommonJS是一种在服务器端广泛使用的模块化规范,它被广泛用于 Node.js 环境中,使用require()和module.exports来导入和导出模块。
AMD
\quad AMD(Asynchronous Module Definition)是一个异步模块加载器规范,它使用define()函数来定义和导入模块。RequireJS是一个流行的AMD实现。
UMD
\quad UMD(Universal Module Definition)是一种通用的模块化方案,它兼容CommonJS、AMD和全局变量的使用场景。UMD允许在不同的环境下使用统一的模块化语法。
ES6模块
\quad ES6 Modules是ECMAScript 6规范的一部分,它是官方推荐的标准模块系统。在现代浏览器中得到广泛支持。它使用import和export关键字来导入和导出模块。在anyGraph中,我们将采用ES6模块化方式。
下面通过一个示例来了解ES6模块的用法:
1)创建模块: 建立一个js文件,在该js文件中实现一组功能代码,并导出公共的对象、函数或类
// moduleA.js
export function add(a, b) {
return a + b;
}
2)使用模块: 在页面或其他模块中使用import导入模块中的对象、函数或类,然后就可以使用了
在模块中使用:
import { add } from './moduleA.js';
console.log(add(12, 4)); // 输出:16
在网页中使用如下:
<script type="module">
import { add } from './moduleA.js';
console.log(add(12, 4)); // 输出:16
</script>
(2) 类
\quad JavaScript是一种基于原型的面向对象语言。这意味着你可以创建自己的类和对象,以及继承和扩展已有的类和对象。
\quad 在ES6版本之前,js通过原型对象来实现类和类的继承。下面是一个简单的示例:
// 定义一个Foo类
function Foo(name) {
this.name = name;
this.type = "FooType";
};
Foo.prototype.getType = function() {
return this.type + ":" + this.name;
};
function Sub(name) {
this.name = name;
};
// 从Foo继承
Sub.prototype = new Foo();
Sub.prototype.getInfo = function() {
return "My name is " + this.name + ", My type is " + this.type ;
};
\quad 在这段代码中创建了 `Foo类和Sub类,且Sub类的原型指向Foo类的实例,可以把这种写法理解为 Sub类从Foo类实现了继承。
\quad ES6采用关键字 class 创建类,并可使用 extends 从一个类继承,这种方式更接近 JAVA 和 C# 等语法风格,也更易理解。下面是一个简单的示例:
// 定义一个Foo类
class Foo {
constructor(name) {
this.name = name;
}
getInfo() {
return this.name;
}
}
// 从Foo继承
class Sub extends Foo {
constructor(name, age) {
super(name);
this.age = age;
}
getInfo() {
return "My name is " + this.name + ", I'm " + this.age + " year old";
}
}
在anyGraph中,我们将采用ES6提供的class方式创建类,并实现类的继承。
(3) 立即执行函数
\quad 在 JavaScript 中,立即执行函数是一种特殊的函数,它在定义后立即执行。这是一种常见的JavaScript编程模式,可以帮助开发者确保代码在特定上下文中运行。这种模式的主要好处是可以在一个独立的命名空间中运行代码,防止全局变量的污染。
以下是一个立即执行函数的例子:
(function() {
// 函数体
})();
\quad 注意这里的括号结构:(function(){}) 中的 () 是一个空的参数列表,表示没有任何输入参数;后面跟着另一个 () 表示立即调用这个匿名函数。通过这种方式,我们可以确保函数内部的变量和函数不会污染全局作用域。同时,如果需要向外部暴露某些接口,可以通过返回一个对象来实现。
\quad 在anyGraph中,一些工具类采用立即执行函数的编程方式,以下代码定义了一个模块,在模块将导出一个工具类。
//math.js
let MathUtil = (function() {
/**
* 将弧度转换为度
* @param {number} angleInRadians 以弧度为单位的角度
* @return {number} 角度(以度为单位)
*/
function toDegrees(angleInRadians) {
return (angleInRadians * 180) / Math.PI;
}
/**
* 将度数转换为弧度
* @param {number} angleInDegrees 以度为单位的角度
* @return {number} 角度(弧度)
*/
function toRadians(angleInDegrees) {
return (angleInDegrees * Math.PI) / 180;
}
/**
* 返回外部可访问的方法
*/
return {
toDegrees,
toRadians
}
})();
export default MathUtil;
3 坐标系
\quad 坐标系是建立图形与数据之间对应关系的参考系。它可以直观方便的描述图形的几何信息、大小、位置。
\quad 在计算机图形学中,从对象的建模,到在不同显示设备上显示、处理图形时均会使用坐标系。例如:在屏幕上会使用像素构成的二维坐标系来表示图形的像素值。
(1) 图形坐标系
\quad 图形坐标系是计算机图形学中使用的坐标系,用于描述和定位图形对象。通常由两个互相垂直的坐标轴组成,分别叫做x轴和y轴。其中x轴表示水平距离,y轴表示垂直距离,这两条轴相交于坐标原点。
\quad 在图形坐标系中,可以通过坐标点来表示二维平面上任何位置,通常用(x,y)的形式表示,其中x表示横坐标,y表示纵坐标。
需要注意的是:
- 在不同的应用程序中,由于不同的应用程序需要处理不同类型的图形和数据,需采用不同的算法和计算方法,因此图形坐标系可能会有不同的含义和用途。
- 在同一应用程序中,图形坐标值在不同的图之间的也会表达不同的含义,例如在SVG图形中,不同的图形之间的坐标值并不能代表其大小尺寸,其坐标单位也可能并不相同。
(2) 屏幕坐标系
\quad 屏幕坐标系(Screen Coordinate System) 是用于表示屏幕上的像素位置的坐标系。它通常是一个以左上角为原点(0,0)的二维直角坐标系,其中水平方向向右为正方向,垂直方向向下为正方向。在屏幕坐标系中,每个像素都可以由其x和y坐标确定。例如,屏幕上的某个像素可能具有坐标(120, 240),这意味着它距离屏幕左侧120个像素,距离屏幕顶部240个像素。
\quad 普通的笛卡尔坐标系统的坐标原点(0,0)位于左下角位置,X轴方向上向右是正值,向左是负值。Y轴方向上向上是正值,向下是负值。如下图所示:

\quad 而屏幕坐标系坐标原点位于左上角,X轴和笛卡尔坐标系的X轴相同,但是Y轴则刚好相反,如下图所示:

\quad Canvas使用的是屏幕坐标系,其原点(0,0)位于Canvas的左上角,而不是屏幕的左上角。
(3) 地理坐标系
\quad 地理坐标系(Geographic Coordinate System)是一个使用三阶球面来定义地球表面位置的坐标系,最常见的地理坐标系使用经纬度来表示地理位置,很明显地理坐标系是球面坐标系统。常见的地理坐标系有:
-
CGCS2000坐标系(China Geodetic Coordinate System 2000): 中国国家测绘局于2008年发布的新一代大地坐标系,是中国国内使用的标准地理坐标系,我国的GPS系统-北斗导航系统以及国家发行的“天地图”,用的是这一套地理坐标系统。
-
WGS84坐标系(World Geodetic System 1984): 由美国国防部制定,是目前全球广泛使用的标准地理坐标系。GPS导航系统就是基于WGS84坐标系的。
-
北京54、西安80: 是我国已经逐渐停止使用的两个地理坐标系统。
经纬度是由地球表面上的一组直线组成的网格,由两个相互垂直的坐标轴组成,分别是经度和纬度。经度是沿赤道方向的南北方向线,以本初子午线为中心,分为东西两部分,东经和西经,表示地球表面的经度。纬度是沿着极点的方向线,表示地球表面的纬度。在地球上,经度是从0°到180°,纬度则是从0°到90°。
(4) 投影坐标系
\quad 我们已经知道地理坐标系是一种球面坐标系,当该系统转移到二维地图上时会出现扭曲。投影变换是利用一定的数学法则,将地球上的经纬网表示到平面上的的理论和方法。
\quad 投影坐标系(Projected Coordinate System),是平面坐标系统,地图单位通常为米。投影坐标系使用基于X,Y值的坐标系统来描述地球上某个点所处的位置。这个坐标系是从地球的近似椭球体投影变换得到的,它对应于某个地理坐标系。
\quad 由于地球是一个赤道略宽两极略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变形,为按照不同的需求缩小误差,就产生了各种投影方式。在图形系统中,常见投影方法包括高斯克里格投影、墨卡托投影和web墨卡托投影。下面介绍几个常见的投影坐标系。
Mercator (墨卡托)
\quad 英文名Mercator投影。假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即得墨卡托投影。如下图所示:
Web Mercator(WEB墨卡托)
\quad 这是一个由Google提出的、为了自家GoogleMap而专门定义的一种投影,是墨卡托投影的一种变种。主要是将地球椭球面当作正球面来投影,这就会导致更大的误差。Web Mercator已成为Google地图和Bing地图等Web地图应用程序的事实上的标准。如下图所示:
高斯克吕格投影
\quad 英文名Gauss Kruger,它是一种横轴等角切圆柱投影。我们把地球看成是地球椭球体,假想用一个椭圆筒横套在其上,使筒与地球椭球的某一经线(称为中央经线)相切,椭圆筒的中心轴位于赤道上,按等角条件将地球表面投影到椭圆筒上,然后将椭圆筒展开成平面。
如下图所示:
4 基础数学知识
\quad 图形系统开发过程中将会涉及一些数学概念,例如几何学、线性代数等。掌握这些数学知识将有助于理解和解决图形相关问题,为算法和计算提供基础。
\quad anyGraph 的坐标转换、图形交互操作等功能中充分应用了这些数据知识,对于图形系统应用开发人员而言,可以略过此部分内容。
(1) 常用三角函数
\quad 三角函数在计算机图形学中扮演着重要的角色,它们可以描述几何图形的形状、位移和旋转等特性。例如,在旋转和缩放等几何变换过程中,三角函数可以用于描述图形在平面上的位置和方向。它可以通过表示角度、旋转角度、旋转轴等参数来表示旋转的特性,从而实现旋转的控制和计算。
\quad 在二维图形编程中,最常使用的三角函数包括正弦(sine, 简称sin)、余弦(cosine, 简称cos)和正切(tangent, 简称tan)。
\quad 下图的左部分是三角函数中sin、cos、tan的定义,右部分以半径、x坐标和y坐标来解释正弦与余弦函数。
定义式
| 名称 | 定义 | 定义 |
|---|---|---|
| 正弦 s i n θ sin \theta sinθ | s i n θ sin \theta sinθ = 对边 / 斜边 | s i n θ sin \theta sinθ = y / r |
| 余弦 c o s θ cos \theta cosθ | c o s θ cos \theta cosθ = 邻边 / 斜边 | c o s θ cos \theta cosθ = x / r |
| 正切 t a n θ tan \theta tanθ | t a n θ tan \theta tanθ = 对边 / 邻边 | t a n θ tan \theta tanθ = y / x |
两角和差公式
- s i n ( α + β ) = s i n α × c o s β + c o s α × s i n β sin(\alpha + \beta) = sin\alpha \times cos\beta + cos\alpha \times sin\beta sin(α+β)=sinα×cosβ+cosα×sinβ
- s i n ( α − β ) = s i n α × c o s β − c o s α × s i n β sin(\alpha - \beta) = sin\alpha \times cos\beta - cos\alpha \times sin\beta sin(α−β)=sinα×cosβ−cosα×sinβ
- c o s ( α + β ) = c o s α × c o s β − s i n α × s i n β cos(\alpha + \beta) = cos\alpha \times cos\beta - sin\alpha \times sin\beta cos(α+β)=cosα×cosβ−sinα×sinβ
- c o s ( α − β ) = c o s α × c o s β + s i n α × s i n β cos(\alpha - \beta) = cos\alpha \times cos\beta + sin\alpha \times sin\beta cos(α−β)=cosα×cosβ+sinα×sinβ
诱导公式
公式一:设α为任意角,终边相同的角的同一三角函数的值相等
- s i n ( 2 π + α ) = s i n ( α ) sin(2\pi + \alpha) = sin(\alpha) sin(2π+α)=sin(α)
- c o s ( 2 π + α ) = c o s ( α ) cos(2\pi + \alpha) = cos(\alpha) cos(2π+α)=cos(α)
- t a n ( 2 π + α ) = t a n ( α ) tan(2\pi + \alpha) = tan(\alpha) tan(2π+α)=tan(α)
公式二:任意角α与-α的三角函数值之间的关系
- s i n ( − α ) = − s i n ( α ) sin(-\alpha) = -sin(\alpha) sin(−α)=−sin(α)
- c o s ( − α ) = c o s ( α ) cos(-\alpha) = cos (\alpha) cos(−α)=cos(α)
- t a n ( − α ) = − t a n ( α ) tan(-\alpha) = -tan(\alpha) tan(−α)=−tan(α)
公式三:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系
- s i n ( π + α ) = − s i n ( α ) sin(\pi + \alpha) = - sin(\alpha) sin(π+α)=−sin(α)
- c o s ( π + α ) = c o s ( α ) cos(\pi + \alpha) = cos(\alpha) cos(π+α)=cos(α)
- t a n ( π + α ) = − t a n ( α ) tan(\pi + \alpha) = - tan(\alpha) tan(π+α)=−tan(α)
公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系
- s i n ( π − α ) = s i n ( α ) sin(\pi - \alpha) = sin(\alpha) sin(π−α)=sin(α)
- c o s ( π − α ) = − c o s ( α ) cos(\pi - \alpha) = - cos(\alpha) cos(π−α)=−cos(α)
- t a n ( π − α ) = t a n ( α ) tan(\pi - \alpha) = tan(\alpha) tan(π−α)=tan(α)
(2) 变换矩阵
\quad 变换矩阵 (Transformation Marices) 是一种数学工具,它可以有效地描述几何图形的变形和变换,并且可以快速地实现几何变换的操作。变换矩阵可以通过平移、旋转、缩放等方式改变几何图形的位置和形状,便于处理图形变换和建模等问题。
\quad 变换矩阵在计算机图形学中有很重要的应用,而向量是图形学中的基本元素,下面讲述的内容均为二维图形变换。
向量
\quad 向量是一个数学概念,它表示一个有方向和大小的量。向量通常用箭头表示,箭头的方向表示向量的方向,长度表示向量的大小。在图形学中,向量可以用于表示几何图形的位置、方向和形状等特性,例如点的位置、线的方向以及面的大小和形状。此外,向量还可以用于实现图形变换,例如平移、旋转、缩放等。
向量的几何表示:
向量的矩阵表示:
[ x y ] \begin{bmatrix}x \\ y \end{bmatrix} [xy]
向量的基本运算:
加减:对应位置进行相加/相减即可,向量的加减将得到一个新向量,在几何中表现为对向量位移:
[ a 1 b 2 ] + [ b 1 b 2 ] = [ a 1 + b 1 a 2 + b 2 ] \begin{bmatrix} a1\\b2 \end{bmatrix} + \begin{bmatrix} b1 \\ b2 \end{bmatrix} = \begin{bmatrix} a1 + b1 \\ a2 + b2 \end{bmatrix} [a1b2]+[b1b2]=[a1+b1a2+b2]
数乘:或者叫标量乘法,指的是将向量和一个常量数字进行相乘,也是对应位置相乘,向量的数乘将得到一个新向量,在几何中表现为对向量缩放:
λ × [ a 1 a 2 ] = [ λ × a 1 λ × a 2 ] \lambda \times \begin{bmatrix} a1\\a2 \end{bmatrix} = \begin{bmatrix} \lambda \times a1 \\ \lambda \times a2 \end{bmatrix} λ×[a1a2]=[λ×a1λ×a2]
点乘:
\quad 两个向量的点乘结果是一个标量,其值等于两向量模长的乘积与它们之间夹角余弦的乘积,如果两个向量的点乘结果为0,那么它们垂直。在二维中,向量a和b的点积根据定义计算公式可以写为:
- a = ( a x , a y ) , b = ( b x , b y ) a = (ax, ay), b = (bx, by) a=(ax,ay),b=(bx,by)
- a × b = a x × b x + a y × b y = ∣ a ∣ ∣ b ∣ c o s ( a , b ) a \times b = ax \times bx + ay \times by = |a||b|cos(a,b) a×b=ax×bx+ay×by=∣a∣∣b∣cos(a,b)
- a × b > 0 , θ < 90 ° ; a × b = 0 , θ = 90 ° ; a × b < 0 , θ > 90 ° a \times b > 0, \theta < 90°; a \times b = 0, \theta = 90°; a \times b < 0, \theta > 90° a×b>0,θ<90°;a×b=0,θ=90°;a×b<0,θ>90°
线性变换
\quad 线性变换是一种特殊的数学变换,它将向量空间中的向量映射到另一个向量空间中。将一个2D向量通过矩阵转换为另一个2D向量就叫作线性变换。
\quad 线性变换是操作空间的一种手段,它能够保持直线变换后依然是直线,并保持原点不动。线性变换满足下面这个等式:
x ′ = a × x + b × y x^\prime = a \times x + b \times y x′=a×x+b×y
y ′ = c × x + d × y y^\prime = c \times x + d \times y y′=c×x+d×y
使用矩阵表达就是:
[ x ′ y ′ ] = [ a b c d ] [ x y ] = x [ a c ] + y [ b d ] = [ a × x + b × y c × x + d × y ] \begin{bmatrix} x^\prime \\ y^\prime\end{bmatrix} = \begin{bmatrix} a & b\\c & d\end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x \begin{bmatrix}a \\ c \end{bmatrix} + y \begin{bmatrix}b \\ d \end{bmatrix} = \begin{bmatrix} a \times x + b \times y \\c \times x + d \times y\end{bmatrix} [x′y′]=[acbd][xy]=x[ac]+y[bd]=[a×x+b×yc×x+d×y]
下面我们看一些常见的线性变换
缩放(比例变换)
\quad 缩放是一种线性变换,是将一个向量(或者点)的 x 和 y 各自进行指定比例的缩放。下图展示了将一个矩形的缩放1.2倍之后的运行效果:
\quad 将缩放前的坐标(x, y)换算到缩放后的新坐标( x ′ x^\prime x′, y ′ y^\prime y′)的等式如下:
x ′ = x × s x \quad x^\prime = x \times sx x′=x×sx
y ′ = y × s y \quad y^\prime = y \times sy y′=y×sy
\quad 在这个等式中,坐标轴的横向缩放倍数记为sx,将原有x坐标乘以它,则可以得出新的横坐标;同时坐标轴的纵向缩放倍数记为sy,将原有y坐标乘以它,则可以得出新的纵坐标。
用矩阵来描述缩放就是下面这个样子:
[ s x 0 0 s y ] \quad\begin{bmatrix} sx & 0 \\0 & sy \end{bmatrix} [sx00sy]
坐标缩放运算过程如下所示:
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] = [ x × s x y × s y ] \quad \begin{bmatrix} x^\prime \\y^\prime \end{bmatrix} = \begin{bmatrix} sx & 0 \\0 & sy \end{bmatrix} \begin{bmatrix} x \\y \end{bmatrix} = \begin{bmatrix} x \times sx \\ y \times sy \end{bmatrix} [x′y′]=[sx00sy][xy]=[x×sxy×sy]
- 当 sx = sy 时,则等比例缩放;
- 当 s > 1时,则图形放大;
- 当 s < 1时,则图形缩小;
- sx = -1 时,x轴对称变换(水平翻转)
- sy = -1 时,y轴对称变换(垂直翻转)
旋转(旋转变换)
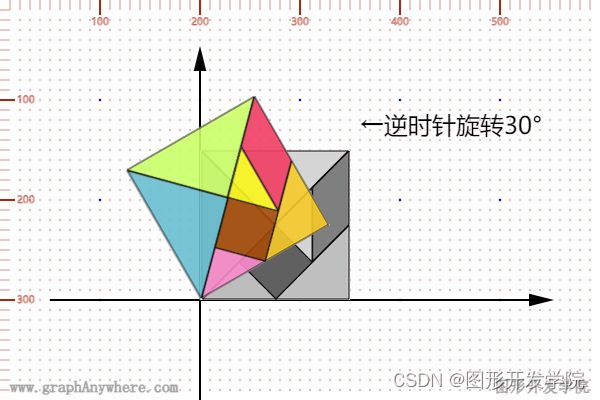
\quad 旋转也是一种线性变换,是指将一个向量(或者点)的 x 和 y 绕着一个定点旋转一定的角度。下图展示了将一个矩形逆时针旋转30度的运行效果:
将旋转前的坐标(x, y)换算到旋转后的新坐标( x ′ x^\prime x′, y ′ y^\prime y′)的等式如下:
x ′ = x × c o s θ − y × s i n θ \quad x^\prime = x \times cos\theta - y \times sin\theta x′=x×cosθ−y×sinθ
y ′ = y × c o s θ + x × s i n θ \quad y^\prime = y \times cos\theta + x \times sin\theta y′=y×cosθ+x×sinθ
用矩阵来描述旋转就是下面这个样子:
[ c o s θ − s i n θ s i n θ c o s θ ] \quad \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos \theta \end{bmatrix} [cosθsinθ−sinθcosθ]
旋转运算过程如下所示:
[ x ′ y ′ ] = [ c o s θ − s i n θ s i n θ c o s θ ] [ x y ] = [ x × c o s θ − y × s i n θ y × c o s θ + x × s i n θ ] \quad \begin{bmatrix} x^\prime \\y^\prime \end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos \theta \end{bmatrix} \begin{bmatrix} x \\y \end{bmatrix} = \begin{bmatrix} x \times cos\theta - y \times sin\theta \\ y \times cos\theta + x \times sin\theta \end{bmatrix} [x′y′]=[cosθsinθ−sinθcosθ][xy]=[x×cosθ−y×sinθy×cosθ+x×sinθ]
错切(shear)
\quad 错切变换也是一种线性变换,本文暂且略过。
平移(平移变换)
\quad 平移就是将一个向量(或者点)的 x 和 y 各自移动一段距离。下图展示了将一个矩形水平移动50,垂直方向移动30后的运行效果:
\quad 将平移前的坐标(x,y)换算到平移后的新坐标( x ′ x^\prime x′, y ′ y^\prime y′)的等式如下:
x ′ = x + d x \quad x^\prime = x + dx x′=x+dx
y ′ = y + d y \quad y^\prime = y + dy y′=y+dy
\quad 在这一组等式中,新坐标系的横向距离差记为dx,将其加到原坐标x坐标值之中,就可以得出新的横坐标了;同时新旧坐标系的纵向距离差记为dy,将其加到旧的y坐标之中,就可以得出新的纵坐标。
用矩形表达运算过程为:
[ x ′ y ′ ] = [ a b c d ] [ x y ] + [ d x d y ] \quad \begin{bmatrix} x^\prime \\ y^\prime\end{bmatrix} = \begin{bmatrix} a & b\\c & d\end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} dx \\ dy \end{bmatrix} [x′y′]=[acbd][xy]+[dxdy]
线性变换是通过一个矩阵与一个向量相乘得出结果,而这里加上了另一个向量,因此平移变换并不属于线性变换。
\quad 想要表达这种计算就得将矩阵扩展为三阶矩阵,使用第三维为常数的 ( d x , d y , 1 ) (dx,dy,1) (dx,dy,1)表示二维平面上的向量。
这种 n + 1 n+1 n+1维表示 n n n维的方法称为—齐次坐标表示法
三阶矩阵如下:
[ 1 0 d x 0 1 d y 0 0 1 ] \quad \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} 100010dxdy1
输入向量也需要升阶,加多一个值为1的第三阶度:
[ x y 1 ] \quad \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} xy1
运算过程:
[ x ′ y ′ w ′ ] = [ 1 0 d x 0 1 d y 0 0 1 ] [ x y 1 ] = x [ 1 0 0 ] + y [ 0 1 0 ] + 1 [ d x d y 1 ] = [ x × 1 + y × 0 + 1 × d x x × 0 + y × 1 + 1 × d y x × 0 + y × 0 + 1 × 1 ] = [ x + d x y + d y 1 ] \quad \begin{bmatrix} x^\prime \\ y^\prime\ \\ w^\prime\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\y \\ 1 \end{bmatrix} = x\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + 1 \begin{bmatrix} dx \\ dy \\ 1 \end{bmatrix} = \begin{bmatrix}x \times 1 &+ &y \times0 & + & 1 \times dx \\x \times 0 &+ &y \times1 & + & 1 \times dy \\x \times 0 &+ &y \times0 & + & 1 \times 1 \end{bmatrix} =\begin{bmatrix} x + dx \\y + dy \\ 1 \end{bmatrix} x′y′ w′ = 100010dxdy1 xy1 =x 100 +y 010 +1 dxdy1 = x×1x×0x×0+++y×0y×1y×0+++1×dx1×dy1×1 = x+dxy+dy1
仿射变换
\quad 仿射变换就是合并线性变换和平移变换的变换类型,在二维图形处理中,仿射变换可以使用一个3*3的矩阵来表示。
有关仿射变换更多内容可以参考:https://www.matongxue.com/madocs/244/
三阶缩放矩阵为:
S ( s x , s y ) = [ s x 0 0 0 s y 0 0 0 1 ] \quad S(sx, sy) = \begin{bmatrix} sx & 0 & 0 \\0 & sy & 0 \\ 0 & 0 & 1 \end{bmatrix} S(sx,sy)= sx000sy0001
三阶旋转矩形为:
R ( θ ) = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] \quad R(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} R(θ)= cosθsinθ0−sinθcosθ0001
三阶平移矩阵为:
T ( d x , d y ) = [ 1 0 d x 0 1 d y 0 0 1 ] \quad T(dx, dy) = \begin{bmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{bmatrix} T(dx,dy)= 100010dxdy1
镜像(mirroring)
\quad 也称之为对称变换或反射变换,是关于x轴、y轴、原点、某条直线的对称变换。
x轴镜像:
S ( − 1 , 1 ) = [ 1 0 0 0 − 1 0 0 0 1 ] \quad S(-1, 1) = \begin{bmatrix} 1 & 0 & 0 \\0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} S(−1,1)= 1000−10001
y轴镜像:
S ( 1 , − 1 ) = [ − 1 0 0 0 1 0 0 0 1 ] \quad S(1, -1) = \begin{bmatrix} -1 & 0 & 0 \\0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} S(1,−1)= −100010001
地理投影坐标系的Y轴以北方向为正,南方向为负。Y轴的数值越大表示该点越向北,数值越小表示该点越向南。这一点与屏幕坐标系是相反的,因此两者在进行坐标转换时将会使用此处讲述的Y轴镜像变换。
原点镜像:
S ( − 1 , − 1 ) = [ − 1 0 0 0 − 1 0 0 0 1 ] \quad S(-1, -1) = \begin{bmatrix} -1 & 0 & 0 \\0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} S(−1,−1)= −1000−10001
组合变换(矩阵乘法)
\quad 组合变换(Composing Transforms)在图形处理中是指将多个变换操作组合在一起,以实现更复杂的图形变换。这些变换操作可以包括平移、旋转、缩放、倾斜等。通过组合变换,我们可以对图形进行多种多样的操作,以满足不同的需求。
上面这张动图经过了3次变换:
- 第一次是顺时针旋转了30°
- 第二次图形缩放了2倍
- 第三次图形水平平移了60,垂直平移了30
\quad 使用矩阵乘法是实现组合变换的一种重要方法,在组合变换中,我们通常先定义一个初始矩阵,然后将多个变换矩阵相乘,以得到最终的变换矩阵。这个过程可以用公式表示为T=A*B,其中T是最终的变换矩阵,A和B是中间的变换矩阵。
上述三次变换的过程如下:
- 建立初始矩阵 = [ 1 0 0 1 0 0 0 0 1 ] = \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} = 110000001
- 计算旋转后矩阵: 初始矩阵 × R ( θ ) 初始矩阵 \times R(\theta) 初始矩阵×R(θ)
- 计算缩放后矩阵: 旋转后矩阵 × S ( s x , s y ) 旋转后矩阵 \times S(sx, sy) 旋转后矩阵×S(sx,sy)
- 计算平移后矩阵: 缩放后矩阵 × T ( d x , d y ) 缩放后矩阵 \times T(dx, dy) 缩放后矩阵×T(dx,dy)
- 应用平移后矩阵,从而计算得到的坐标,最后重绘图形。
程序实现
建立初始矩阵
\quad 刚刚我们讲述了使用3*3的矩阵来表示二维图形中的缩放、旋转、平移等变换,由于最后一行始终是 [0, 0, 1],因此只需要传矩阵的前两行,共6个值的一维数组[a,b,c,d,e,f]来构建矩阵。该数组对应变换矩阵的位置如下:
[ a c e b d f 0 0 1 ] \quad \begin{bmatrix} a & c & e \\ b & d & f \\ 0 & 0 & 1 \end{bmatrix} ab0cd0ef1
其中:
- a表示水平缩放
- b表示垂直倾斜
- c表示水平倾斜
- d表示垂直缩放
- e表示水平移动
- f表示垂直移动
建立初始矩阵程序代码如下:
/**
* 变换矩阵
*/
class Transform {
/**
* 创建Transform.
* @return {Transform} 初始矩阵.
*/
static create() {
return [1, 0, 0, 1, 0, 0];
}
/**
* 给矩阵赋值
* @return {Transform} 赋值后矩阵.
*/
static set(transform, a, b, c, d, e, f) {
transform[0] = a;
transform[1] = b;
transform[2] = c;
transform[3] = d;
transform[4] = e;
transform[5] = f;
return transform;
}
}
矩阵相乘
矩阵相乘计算规则:
[ a 1 c 1 e 1 b 1 d 1 f 1 0 0 1 ] × [ a 2 c 2 e 2 b 2 d 2 f 2 0 0 1 ] = [ a 1 × a 2 + c 1 × b 2 a 1 × c 2 + c 1 × d 2 a 1 × e 2 + c 1 × f 2 + e 1 b 1 × a 2 + d 1 × b 2 b 1 × c 2 + d 1 × d 2 b 1 × e 2 + d 1 × f 2 + f 1 0 0 1 ] \begin{bmatrix} a1 & c1 & e1 \\ b1 & d1 & f1 \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} a2 & c2 & e2 \\ b2 & d2 & f2 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} a1 \times a2 + c1 \times b2 & a1 \times c2 + c1 \times d2 & a1 \times e2 + c1 \times f2 + e1 \\ b1 \times a2 + d1 \times b2 & b1 \times c2 + d1 \times d2 & b1 \times e2 + d1 \times f2 + f1 \\ 0 & 0 & 1 \end{bmatrix} a1b10c1d10e1f11 × a2b20c2d20e2f21 = a1×a2+c1×b2b1×a2+d1×b20a1×c2+c1×d2b1×c2+d1×d20a1×e2+c1×f2+e1b1×e2+d1×f2+f11
矩阵相乘程序代码如下:
/**
* 将两个变换的基础矩阵相乘,并返回第一个变换的结果。
* @param {Transform} transform1 矩阵1.
* @param {Transform} transform2 矩阵2.
* @return {Transform} 变换的结果,同时也将改变目标矩阵的值.
*/
static multiply(transform1, transform2) {
let [a1, b1, c1, d1, e1, f1] = transform1;
let [a2, b2, c2, d2, e2, f2] = transform2;
transform1[0] = a1 * a2 + c1 * b2;
transform1[1] = b1 * a2 + d1 * b2;
transform1[2] = a1 * c2 + c1 * d2;
transform1[3] = b1 * c2 + d1 * d2;
transform1[4] = a1 * e2 + c1 * f2 + e1;
transform1[5] = b1 * e2 + d1 * f2 + f1;
return transform1;
}
缩放、旋转、平移
\quad 计算规则我们已经在上面分析过了,其代码实现如下:
/**
* 在矩阵中增加旋转量
* @param {Transform} transform 变换前的矩阵.
* @param {number} angle 旋转角度(弧度).
* @return {Transform} 旋转后的矩阵.
*/
static rotate(transform, angle) {
let cos = Math.cos(angle);
let sin = Math.sin(angle);
let tmp_ = new Array(6);
return this.multiply(transform, this.set(tmp_, cos, sin, -sin, cos, 0, 0));
}
/**
* 在矩阵中增加缩放量
* @param {Transform} transform 变换前的矩阵.
* @param {number} x 水平方向缩放倍数.
* @param {number} y 垂直方向缩放倍数.
* @return {Transform} 缩放后的矩阵.
*/
static scale(transform, sx, sy=sx) {
let tmp_ = new Array(6);
return this.multiply(transform, this.set(tmp_, sx, 0, 0, sy, 0, 0));
}
/**
* 在矩阵中增加平移量
* @param {Transform} transform 变换前的矩阵.
* @param {number} dx 水平方向平移量.
* @param {number} dy 垂直方向平移量.
* @return {Transform} 平移后的矩阵.
*/
static translate(transform, dx, dy) {
let tmp_ = new Array(6);
return this.multiply(transform, this.set(tmp_, 1, 0, 0, 1, dx, dy));
}
应用矩阵,计算新的坐标
\quad 矩阵进行变形之后,其目的是"应用"(即让图形发生变换,对于多边形而言是将原有坐标转换为新的坐标),从而在Canvas中将图形绘制出来,计算过程如下:
{ x ′ = a × x + c × y + e y ′ = b × x + d × y + f \quad \begin{cases}x^\prime = a \times x + c \times y + e \\ y^\prime = b \times x + d \times y + f \end{cases} {x′=a×x+c×y+ey′=b×x+d×y+f
这部分的代码如下:
/**
* 使用矩阵变换坐标的值。
* @param {Transform} transform 变换矩阵.
* @param {Array} coordinate 原坐标,格式为[x,y].
* @param {Boolean} precision 返回值是否保留小数.
* @return {Array} 返回变换之后的坐标
*/
static apply(transform, coordinates, precision = true) {
let dest = [];
let x = coordinates[0],
y = coordinates[1];
dest[0] = transform[0] * x + transform[2] * y + transform[4];
dest[1] = transform[1] * x + transform[3] * y + transform[5];
return dest;
}
练习一下
- 平移练习
let coords = [[50,200], [100,00], [150,200]];
let trans = Transform.create();
Transform.translate(trans, 50, 50);
let dest = [];
coords.forEach(coord => {
dest.push(Transform.apply(trans, coord));
});
console.info(dest.join(",")); // 100,250,150,50,200,250
- 缩放练习
let coords = [[200,500], [300,100], [400,500]]
let trans = Transform.create();
Transform.scale(trans, 0.5, 0.5);
let dest = [];
coords.forEach(coord => {
dest.push(Transform.apply(trans, coord));
});
console.info(dest.join(",")); // 100,250,150,50,200,250
- 旋转练习
let coords = [[250,-100], [50,-150], [250,-200]];
let trans = Transform.create();
Transform.rotate(trans, toRadians(90));
let dest = [];
coords.forEach(coord => {
dest.push(Transform.apply(trans, coord));
});
console.info(dest.join(",")); // 100,250,150,50,200,250
- 组合练习
let coords = [[150,450], [250,50], [350,450]];
let trans = Transform.create();
Transform.scale(trans, 0.5, 0.5);
Transform.translate(trans, 50, 50);
let dest = [];
coords.forEach(coord => {
dest.push(Transform.apply(trans, coord));
});
console.info(dest.join(",")); // 100,250,150,50,200,250
(3) 坐标系转换
\quad 坐标系转换是指在空间实体的位置描述过程中,将一种坐标系统变换到另一种坐标系统的过程。
\quad 图形渲染时,无论源数据采用了哪种坐标系,都需要转换为屏幕坐标系后进行渲染,这就需要使用到本章所讲述的变换矩阵的内容,关于这部分实现请参见图形开发实战-进阶篇一的第五章:图形交互操作。
\quad 图形系统开发实战-基础篇 第七章变形操作 中,讲述了通过 Canvas 渲染上下文对象提供的矩阵变换的一些知识,通过 矩阵变换 可实现图形的平移、缩放和旋转等操作。这里又从数学的角度讲述了 矩阵变换的原理和过程,这些知识在 “第五章 图形的交互 平移和缩放” 中将会充分应用到。
\quad 这部分的内容比较枯燥,好消息是 anyGraph 已经将 矩阵操作封装到了库中,对于仅仅是图形应用的开发人员,可以略过具体的实现,通过其提供的 API 即可实现绝大多数的图形交互功能。
\quad “图形系统实战开发-进阶篇 第一章 基础知识” 的内容讲解到这里就结束了,如果觉得对你有帮助有收获,可以关注我们的官方账号,持续关注更多精彩内容。
相关资料
▶ 系列教程及代码资料:https://GraphAnyWhere.com
▶ 图形系统开发实战课程:进阶篇(上)——前言
作者信息
作者 : 图形开发学院
CSDN: https://blog.csdn.net/2301_81340430?type=blog
官网:https://graphanywhere.com