多项式加法(链表)
笔者最近正在学习数据结构,碰到了这样一个问题——如何用链表实现多项式的加法?因书上仅给出了数组法的代码,所以笔者尝试自己解决这个问题。为此,笔者写本文来记录思考过程。
思路
一、创建合适的链表
a.分析
百度百科这样描述多项式——”在数学中,几个单项式的和,叫做多项式。”就像多项式由一个个单项式相加而成,链表也由一个个节点连接而成。只是,+连接单项式,指针连接节点。
多项式:
链表:
因此,一个节点应该存放一个单项式:
b.代码
typedef struct Polynomial // 多项式
{
int Coefficient; // 系数
int Exponent; // 指数
} Polynomial;
typedef struct Node // 节点
{
Polynomial Poly;
struct Node* Next;
} Node;
typedef Node* List; // 多项式的项在链表中按指数由大到小排列二、对链表进行操作
a.初始化节点
/*
参数:1个:待初始化的节点的指针
结果:节点中的系数和指数都初始化为0
*/
void ZeroPolynomial(Node* Ptr)
{
if (Ptr != NULL) // 防止传入空指针
{
Ptr->Poly.Coefficient = 0; // 系数初始化为0
Ptr->Poly.Exponent = 0; // 指数初始化为0
Ptr->Next = NULL;
}
}b.创建表头
/*
参数:无
结果:创建多项式的表头
返回:若成功创建,返回表头指针;否则,返回NULL
*/
List CreateHeader(void)
{
List Header;
Header = (List)malloc(sizeof(Node));
if (Header == NULL)
{
ferror("Wrong");
return NULL;
}
ZeroPolynomial(Header); // 初始化表头
return Header;
}c.创建节点
/*
参数:1个:多项式的表头
结果:在链表后创建一个节点,并初始化系数和指数为0
返回:若成功创建,返回创建得节点的指针;否则,返回NULL
*/
Node* CreateNode(List Header)
{
Node* Ptr, * Tmp; // Ptr -- 接收创建得节点的指针
// Tmp -- 临时存放指针,用于寻找链表末尾
Ptr = (Node*)malloc(sizeof(Node));
if (Ptr == NULL)
{
ferror("Wrong");
return NULL;
}
ZeroPolynomial(Ptr); // 初始化节点
Tmp = Header; // 寻找链表末尾
while (Tmp->Next != NULL)
Tmp = Tmp->Next;
Tmp->Next = Ptr; // 将创建得节点添加至链表末尾
return Ptr;
}三、多项式加法
a.分析
以这两个多项式作为例子
多项式加法遵从一个原则——指数相同,系数相加。由于是链表,我们需要一个一个节点比较指数大小。不过,可能会出现某一多项式先结束,即到达链表末尾。同时,我们还要考虑多项式1或2的指数是否与结果中的上一个单项式的指数相同,除了多项式1和2指数相同的情况。
b.代码
/*
参数:2个:多项式1的表头;多项式2的表头
结果:将多项式1和多项式2相加,并存放在列表中,按指数由大到小排列
返回:返回相加后的多形式的表头
*/
List AddPolynomial(List Header1, List Header2)
{
List SumHeader; // 求和结果的表头
Node* Tmp1, * Tmp2, * SumTmp; // Tmp1 -- 接收多项式1的链表的指针;Tmp2 -- 接受多项式2的链表的指针
// 接收结果的链表的指针
SumHeader = CreateHeader();
SumTmp = CreateNode(SumHeader);
Tmp1 = Header1->Next;
Tmp2 = Header2->Next;
/*
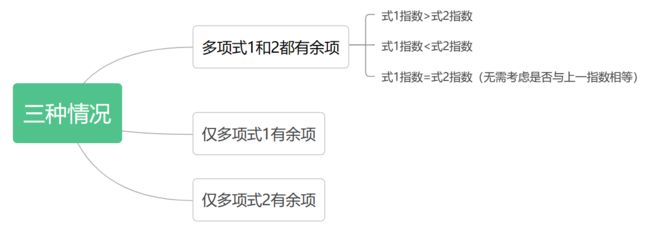
三种情况:
一、多项式1和多项式2都有余项 -- 1) 式1指数 > 式2指数
2) 式1指数 < 式2指数
3) 式1指数 = 式2指数(一定与现节点的指数相异)
二、仅多项式1有余项
三、仅多项式2有余项
除 一/3)外,需进一步考虑式子的指数是否与现节点的指数相同 -- 相异:创建新的节点
相同:在原来的基础上相加
*/
while (Tmp1 != NULL || Tmp2 != NULL) // 某一个多项式仍有余项
{
// 一、多项式1和多项式2都有余项
if (Tmp1 != NULL && Tmp2 != NULL)
{
// 1)式1指数 > 式2指数
if (Tmp1->Poly.Exponent > Tmp2->Poly.Exponent)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp1->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp1->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp1->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp1->Poly.Coefficient;
Tmp1 = Tmp1->Next; // 多项式1的指针移至下一项
}
// 2)式1指数 < 式2指数
else if (Tmp1->Poly.Exponent < Tmp2->Poly.Exponent)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp2->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader);
SumTmp->Poly.Coefficient = Tmp2->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp2->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp2->Poly.Coefficient;
Tmp2 = Tmp2->Next; // 多项式2的指针移至下一项
}
// 3)式1指数 = 式2指数(一定与现节点的指数相异)
else if (Tmp1->Poly.Exponent == Tmp2->Poly.Exponent)
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp1->Poly.Coefficient + Tmp2->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp1->Poly.Exponent;
Tmp1 = Tmp1->Next; // 多项式1和多项式2的指针移至下一项
Tmp2 = Tmp2->Next;
}
}
// 二、仅多项式1有余项
else if (Tmp1 != NULL && Tmp2 == NULL)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp1->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp1->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp1->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp1->Poly.Coefficient;
Tmp1 = Tmp1->Next; // 多项式1的指针移至下一项
}
// 三、仅多项式2有余项
else if (Tmp1 == NULL && Tmp2 != NULL)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp2->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp2->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp2->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp2->Poly.Coefficient;
Tmp2 = Tmp2->Next; // 多项式2的指针移至下一项
}
}
SumTmp = SumHeader->Next; // 消除个别情况下多余的节点
if (SumTmp->Next != NULL)
{
SumHeader->Next = SumTmp->Next;
free(SumTmp);
}
return SumHeader;
}注意:部分情况可能会产生多余的节点1,即第一个节点,需要进行删除,即以下代码:
SumTmp = SumHeader->Next; // 消除个别情况下多余的节点
if (SumTmp->Next != NULL)
{
SumHeader->Next = SumTmp->Next;
free(SumTmp);
}测试结果:
四、完整代码
/* List.h -- 链表头文件 */
#include
#include
#ifndef LIST_H_
#define LIST_H_
typedef struct Polynomial // 元素
{
int Coefficient; // 系数
int Exponent; // 指数
} Polynomial;
typedef struct Node // 节点
{
Polynomial Poly;
struct Node* Next;
} Node;
typedef Node* List; // 多项式的项在链表中按指数由大到小排列
List CreateHeader(void); // 创建多项式的表头
Node* CreateNode(List Header); // 创建一个节点
void ZeroPolynomial(Node* Ptr); // 使节点中的系数和指数的值都为0
List AddPolynomial(List Header1, List Header2); // 两个多项式求和
#endif /* List.c -- 操作链表得函数的定义 */
#include "List.h"
/*
参数:1个:待初始化的节点的指针
结果:节点中的系数和指数都初始化为0
*/
void ZeroPolynomial(Node* Ptr)
{
if (Ptr != NULL) // 防止传入空指针
{
Ptr->Poly.Coefficient = 0; // 系数初始化为0
Ptr->Poly.Exponent = 0; // 指数初始化为0
Ptr->Next = NULL;
}
}
/*
参数:1个:多项式的表头
结果:在链表后创建一个节点,并初始化系数和指数为0
返回:若成功创建,返回创建得节点的指针;否则,返回NULL
*/
Node* CreateNode(List Header)
{
Node* Ptr, * Tmp; // Ptr -- 接收创建得节点的指针
// Tmp -- 临时存放指针,用于寻找链表末尾
Ptr = (Node*)malloc(sizeof(Node));
if (Ptr == NULL)
{
ferror("Wrong");
return NULL;
}
ZeroPolynomial(Ptr); // 初始化节点
Tmp = Header; // 寻找链表末尾
while (Tmp->Next != NULL)
Tmp = Tmp->Next;
Tmp->Next = Ptr; // 将创建得节点添加至链表末尾
return Ptr;
}
/*
参数:无
结果:创建多项式的表头
返回:若成功创建,返回表头指针;否则,返回NULL
*/
List CreateHeader(void)
{
List Header;
Header = (List)malloc(sizeof(Node));
if (Header == NULL)
{
ferror("Wrong");
return NULL;
}
ZeroPolynomial(Header); // 初始化表头
return Header;
}
/*
参数:2个:多项式1的表头;多项式2的表头
结果:将多项式1和多项式2相加,并存放在列表中,按指数由大到小排列
返回:返回相加后的多形式的表头
*/
List AddPolynomial(List Header1, List Header2)
{
List SumHeader; // 求和结果的表头
Node* Tmp1, * Tmp2, * SumTmp; // Tmp1 -- 接收多项式1的链表的指针;Tmp2 -- 接受多项式2的链表的指针
// 接收结果的链表的指针
SumHeader = CreateHeader();
SumTmp = CreateNode(SumHeader);
Tmp1 = Header1->Next;
Tmp2 = Header2->Next;
/*
三种情况:
一、多项式1和多项式2都有余项 -- 1) 式1指数 > 式2指数
2) 式1指数 < 式2指数
3) 式1指数 = 式2指数(一定与现节点的指数相异)
二、仅多项式1有余项
三、仅多项式2有余项
除 一/3)外,需进一步考虑式子的指数是否与现节点的指数相同 -- 相异:创建新的节点
相同:在原来的基础上相加
*/
while (Tmp1 != NULL || Tmp2 != NULL) // 某一个多项式仍有余项
{
// 一、多项式1和多项式2都有余项
if (Tmp1 != NULL && Tmp2 != NULL)
{
// 1)式1指数 > 式2指数
if (Tmp1->Poly.Exponent > Tmp2->Poly.Exponent)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp1->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp1->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp1->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp1->Poly.Coefficient;
Tmp1 = Tmp1->Next; // 多项式1的指针移至下一项
}
// 2)式1指数 < 式2指数
else if (Tmp1->Poly.Exponent < Tmp2->Poly.Exponent)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp2->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader);
SumTmp->Poly.Coefficient = Tmp2->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp2->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp2->Poly.Coefficient;
Tmp2 = Tmp2->Next; // 多项式2的指针移至下一项
}
// 3)式1指数 = 式2指数(一定与现节点的指数相异)
else if (Tmp1->Poly.Exponent == Tmp2->Poly.Exponent)
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp1->Poly.Coefficient + Tmp2->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp1->Poly.Exponent;
Tmp1 = Tmp1->Next; // 多项式1和多项式2的指针移至下一项
Tmp2 = Tmp2->Next;
}
}
// 二、仅多项式1有余项
else if (Tmp1 != NULL && Tmp2 == NULL)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp1->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp1->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp1->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp1->Poly.Coefficient;
Tmp1 = Tmp1->Next; // 多项式1的指针移至下一项
}
// 三、仅多项式2有余项
else if (Tmp1 == NULL && Tmp2 != NULL)
{
// 考虑式子的指数是否与现节点的指数相同
if (Tmp2->Poly.Exponent != SumTmp->Poly.Exponent) // 相异
{
SumTmp = CreateNode(SumHeader); // 创建新的节点
SumTmp->Poly.Coefficient = Tmp2->Poly.Coefficient;
SumTmp->Poly.Exponent = Tmp2->Poly.Exponent;
}
else // 相同
SumTmp->Poly.Coefficient += Tmp2->Poly.Coefficient;
Tmp2 = Tmp2->Next; // 多项式2的指针移至下一项
}
}
SumTmp = SumHeader->Next; // 消除个别情况下多余的节点
if (SumTmp->Next != NULL)
{
SumHeader->Next = SumTmp->Next;
free(SumTmp);
}
return SumHeader;
}/* Polynomial.c -- 测试程序 */
#include "List.h"
void Input(List Header)
{
int coefficient, exponent;
Node* ptr;
ptr = CreateNode(Header);
printf("Enter coefficient-> ");
scanf("%d", &coefficient);
getchar();
printf("Enter exponent-> ");
scanf("%d", &exponent);
getchar();
ptr->Poly.Coefficient = coefficient;
ptr->Poly.Exponent = exponent;
}
void Output(List Header)
{
Node* ptr;
ptr = Header->Next;
while (ptr != NULL)
{
printf("%dX^%d", ptr->Poly.Coefficient, ptr->Poly.Exponent);
if ((ptr = ptr->Next) != NULL)
printf(" + ");
}
putchar('\n');
}
void getch(char* ch)
{
*ch = getchar();
while (getchar() != '\n')
continue;
}
int main()
{
List Header1, Header2, SumHeader;
char ch;
Header1 = CreateHeader();
Header2 = CreateHeader();
printf("Enter the first polynomial (type n to exit).\ny/n-> ");
getch(&ch);
while (ch != 'n')
{
Input(Header1);
printf("y/n-> ");
getch(&ch);
}
printf("Enter the second polynomial (type n to exit).\ny/n-> ");
getch(&ch);
while (ch != 'n')
{
Input(Header2);
printf("y/n-> ");
getch(&ch);
}
SumHeader = AddPolynomial(Header1, Header2);
Output(Header1);
Output(Header2);
Output(SumHeader);
return 0;
}