（2024，仅高频分量的蓝噪声与高斯噪声线性插值，时变噪声）扩散模型的蓝噪声

Blue noise for diffusion models

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

目录

0. 摘要

1. 简介

2. 相关工作

3. 方法

3.1 相关噪声

3.2 具有时变噪声的扩散模型

3.3 利用矫正映射的数据样本相关性

4. 实验

5. 结论

---

0. 摘要

大多数现有的扩散模型在训练和所有时间步骤的采样中使用高斯噪声，这可能无法最优地考虑去噪网络重建的频率内容。尽管相关噪声在计算机图形学中有各种应用，但其在改进训练过程方面的潜力尚未得到充分探索。在本文中，我们引入了一种新颖且通用的扩散模型类别，考虑了图像内部和图像之间的相关噪声。更具体地说，我们提出了一个时变噪声模型，将相关噪声纳入训练过程，以及一种快速生成相关噪声掩码的方法。我们的模型建立在确定性（deterministic）扩散模型基础上，并利用蓝噪声（blue noise），相对于仅使用高斯白噪声（随机噪声），有助于提高生成质量。此外，我们的框架允许在单个小批次中引入图像之间的相关性以改善梯度流。我们使用我们的方法在各种数据集上进行了定性和定量评估，在 FID 指标方面相对于现有的确定性扩散模型实现了不同任务的改进。在接受后，我们将发布代码和已训练模型。

1. 简介

在这篇论文中，我们提出了一种支持具有时变噪声扩散过程的新型扩散模型。我们的目标是利用相关噪声（correlated noise），例如蓝噪声（blue noise）（[Ulichney 1987]），以增强生成过程。蓝噪声的特点是其功率谱在低频区域没有能量。我们的关注点是蓝噪声掩码（blue noise mask）（[Ulichney 1999]），它们提供具有蓝噪声特性的噪声轮廓。我们建议使用这些蓝噪声掩码来设计基于扩散的生成建模的时变噪声。为扩散生成这样的相关噪声掩码是一个耗时的过程，因为它可能需要实时生成数千到数百万个掩码。为了解决这个问题，我们提出了一种有效的方法，可以实时生成适用于低维和高维图像的高斯蓝噪声掩码。

2. 相关工作

蓝噪声（blue noise）。蓝噪声是一种以高频信号和缺失低频信号为特征的噪声类型。它在计算机图形学中有许多应用。

• 其中一种应用是蓝噪声掩码的使用，如 Ulichney [1993] 介绍的，用于扰动（dithering）以通过蓝噪声掩码增强感知质量。
• 蓝噪声掩码也被用于渲染中，以改善错误的分布，如 Georgiev 和 Fajardo [2016] 以及 Heitz 和 Belcour [2019] 的研究所示。
• 关于渲染中蓝噪声与去噪之间的关系已经由 Chizhov 等人 [2022] 和Salaün等人 [2022] 进一步探讨，揭示了将蓝噪声与低通滤波器结合可以减少感知错误。

为了利用蓝噪声掩码的有利去噪特性，我们建议将它们用作扩散式生成建模中数据的加性噪声。

3. 方法

基于扩散的生成模型包括两个关键过程：正向过程和反向过程。在正向过程中，引入了噪声，表示为 ，以通过乘以由离散时间参数 确定的因子来损坏初始图像 x_0。这里，x_0 表示从训练数据分布（表示为 _0）中采样的实际图像。时间步 的范围从 0 到 - 1，其中 是离散时间步的总数。损坏的图像以及相应的时间步 随后被用作训练神经网络 _ (x_ , ) 的输入。

在反向过程中，训练好的网络用于去噪纯噪声并生成新图像。图 2 说明了这个过程。从高斯噪声（蓝色分布）开始，图像通过网络迭代传递，最终产生一个完全去噪的图像，与目标分布（红色分布）一致。过程的中间步骤涉及噪声和图像的混合。图中可见三个示例。随着执行更多时间步骤（ 接近 0），图像质量提高，更多细节出现。在这个例子中，中间噪声从高斯噪声过渡到高斯蓝噪声，遵循第 3.2 节的时变时间表。

本节探讨了两个不同轴上的相关性：噪声中像素之间的相关性，以及一个小批次内图像之间的相关性。为了展示噪声掩码和图像之间的相关性的影响，我们构建了一个具有时变噪声的确定性扩散过程，按照 Heitz 等人 [2023] 的工作，即 IADB 方法。出于简单和公平的一对一比较，我们的方法是在保留其特征和超参数（除了我们方法中描述的新参数）的基础上构建的 IADB。但我们的方法足够通用，可以在其他现有的生成扩散过程的基础上进行探索。对于 IADB，正向和反向过程以及目标函数的定义如下： 

其中，_0 是目标图像， ∼ N(0, ) 是随机的高斯噪声，_ 和 _(−1) 是两个混合系数。网络模型被称为 _，接受两个输入参数：一个损坏的图像 x_ 和时间步长 。IADB 还存在一个随机形式，但本文将重点放在确定性变体上，因为它更为稳定。 

3.1 相关噪声

在确定性扩散过程中，噪声掩码（noise masks）用作反向过程的初始化，以生成图像，并在每个训练步骤中用于损坏目标图像。训练期间的掩码生成是一个关键因素，必须满足特定要求。该过程必须是随机的，以在每次迭代时产生不同的掩码，从而减少过拟合并增加生成结果的多样性。掩码生成还必须具有快速计算的特性，因为它在每个训练步骤中都被使用。

高斯噪声自然符合这些要求，但并非所有相关掩码方法都是如此。特别是，IADB 使用从具有零均值和单位协方差矩阵的多元高斯分布生成的掩码。创建相关噪声，如蓝噪声，需要一个非单位协方差矩阵。蓝噪声掩码的协方差矩阵可以从一组掩码中估计出来。我们使用 Ulichney [1993] 的目标函数进行模拟退火（simulated annealing），生成了一万个蓝噪声掩码。虽然这种方法产生了高质量的掩码，但确实需要相当多的优化时间。然后，通过对示例掩码的相关矩阵进行平均，可以计算蓝噪声的协方差矩阵 Σ。

为了创建具有指定协方差矩阵 Σ 的噪声掩码，对 Σ 应用 Cholesky 分解，得到一个下三角矩阵 （^ = Σ）。最后，随机向量与 相乘，以有效地生成所需的噪声掩码：

其中，ϵ∼N(0,I) 是单位方差的高斯分布。

图 3 显示了使用等式 (4) 生成的高斯蓝噪声掩码的一个实现。在 中的每行或每列表示噪声掩码的像素索引。在 中的每个单元格表示噪声掩码中像素之间的相关强度。正值对应于表示正相关的亮单元格。类似地，负值对应于表示负相关的暗单元格。对于每个像素，只有其相邻像素的值与零差距较大，而其他非相邻像素的值接近零，如白色和黑色线所示。请注意，本文中我们将 b 称为高斯蓝噪声，但与 Ahmed 等人 [2022] 的高斯蓝噪声方法不同。

更高的维度。当 矩阵是高维时，矩阵-向量乘法在计算上是昂贵的。直接增加矩阵大小以生成高维噪声比使用现代机器学习框架（如 PyTorch [Paszke等人，2017]）生成（不相关的）高斯噪声更慢。由于噪声生成在每个训练步骤中都被使用，开销应该保持最小。因此，为了生成更高维度的噪声掩码，我们采用了 Kollig 和 Keller [2002] 的方法，用于生成我们的蓝噪声掩码：对一组较低维度的掩码进行填充。

更具体地说，为了生成一批高维度的高斯蓝噪声掩码，使用等式 (4) 在分辨率 64 x 64 生成一个更大的批次，其中 L∈R^(64^2 × 64^2)。然后将 64^2 的掩码填充到更大的平铺（tiles）中，以获得更高维度的高斯蓝噪声掩码。因此，生成 256x256 分辨率的高斯蓝噪声的计算开销是可以忽略的。

图 1 显示了通过填充来生成分辨率为 128 x 128 的高斯蓝噪声的示例。对于高维度掩码使用填充会在填充的平铺之间创建接缝。这种伪影在实际中几乎看不到，并且通过该方法的低开销得以补偿。我们在附录文档第 3 节中提供了不同分辨率的掩码，以及高斯蓝噪声的相应频率功率谱，演示了使用我们的填充方法在不同分辨率下保持蓝噪声属性。

（注：在相邻像素之间补零，导致图像频谱只有高频分量，没有低频分量）

3.2 具有时变噪声的扩散模型

使用单个矩阵 只能生成单个相关性。对于扩散模型，在每个时间步引入模型内的相关性的量需要进行控制。可以从编码两种相关性类型的两个固定矩阵计算时变的 ：

其中 L_w​ 和 L_b​ 表示两个不同的矩阵，γ_t​ 是混合系数（注：在白噪声 white 矩阵和蓝噪声 blue 矩阵之间插值，获得混合噪声，如算法 1 所示）。基于此，正向过程被定义为： 

通过这个前向过程，基于时间步 对高斯噪声和高斯蓝噪声进行插值。更一般地，该模型支持基于 _ 对任意两种噪声类型进行平滑插值。图 4 显示了从高斯噪声插值到高斯蓝噪声的线性插值的示例。通过离散傅立叶变换（DFT）计算的相应频率功率谱显示，低频区域的能量从左到右逐渐减小。

接下来，前向过程需要被反转以定义后向过程。基于 和前向过程的定义，我们可以推导出后向步骤如下：

详细的推导可以在补充文件第1节中找到。这里，L_w​ 是代表高斯（白色）噪声的单位矩阵，L_b​ 是在方程（4）中定义的矩阵。当 L_b​=L_w​ 时，我们的模型回退到 IADB。当 L_b​ ≠ L_w​ 时，我们得到一个具有时变噪声的更一般模型。

在 IADB 中，网络被设计成仅学习项

其中 L_t​ 在他们的情况下只是一个单位矩阵。在这里，我们可以训练网络学习方程（7）中的两个项。一个蛮力的方法是使用两个神经网络。然而，这不实际，因为它将引入比 IADB 更多的计算。我们选择输出一个 6 通道的图像，表示两个项为两个 3 通道图像，分别表示为 f'_θ​(x_t​,t) 和 f''_θ​(x_t​,t)。所以，期望的网络输出变为如下两项：

因此，损失函数变为： 

请注意，尽管我们的模型是使用时变噪声进行训练的，但在反向过程中仍然是确定性的。反向过程始于初始的高斯噪声，在中间的时间步骤中不需要额外的噪声。相反，网络学会以时变去噪的方式引导反向过程。

前向、反向和噪声生成的步骤总结在算法 1 到 3 中。按照 Heitz 等人 [2023] 的方法，在算法 2 中，我们将 get_alpha（ 调度器）视为线性函数（_ = /），但它也可以是非线性函数。 接下来，我们将 get_gamma 定义为一个通用的基于 sigmoid 的函数，如方程（9）所示。在方程（8）中的加权项 (γt​−γt−1​)/(αt​−αt−1​) 自动考虑了 调度器和 调度器之间的差异。当  γt​−γt−1​ 很小时，f′′θ​(xt​,t) 的贡献减小。这与方程（7）中描述的反向过程一致，其中当 γt​−γt−1​ 很小时，f′′θ​(xt​,t) 不太重要。

噪声调度器。受 Chen [2023] 的研究启发，调度器的选择特别地随着图像分辨率增加而变得重要。我们将 get_gamma，即 -调度器，参数化为一个基于 sigmoid 的函数，以控制两种噪声之间的插值。更具体地说，根据 Chen [2023] 的方法，-调度器由 3 个参数参数化：start​, send​, τ： 

其中，σ(x) = 1/(1+e^x)，而 t 是时间步长。

由于不知道如何提前设置 start​,send​,τ，除了优化网络参数，我们考虑优化它们，其中 start​∈[−3,0)，send​∈(0,3]，τ∈[0.01,1000.0]。在初始实验中，我们发现 start​ 和 send​ 稳定收敛到约为 0 和 3，而 τ 收敛到约为 0.2 或保持增加，具体取决于图像分辨率。与此同时，我们发现优化这 3 个参数需要额外的迭代才能收敛，并使网络的训练更加困难，因为它们在迭代中发生变化。

为了使这 3 个参数的选择更为实际，我们选择固定 sstart​=0，send​=3 并根据图像分辨率设置 τ：对于 128x128 的图像，τ=0.2，对于 64x64 的图像，τ=1000。具有不同 τ 值的 γ−调度器曲线显示在插图中。 我们在补充文件第 2 节中总结了我们在所有实验中使用的这 3 个参数的值。 

讨论。我们的时变噪声模型提供更多能力，来为 γt 选择数据相关调度器，以改进去噪过程。一个潜在的问题是，我们需要额外的迭代来搜索 -调度器的最佳参数。为了缓解这个问题，我们提出了一个实际的解决方案，即基于我们的初始优化固定 τ。但如何更高效地选择 -调度器需要在未来进行更多研究。

3.3 利用矫正映射的数据样本相关性

前面的段落已经演示了在像素之间使用相关的噪声来增强扩散过程。相关性也可以在单个小批次中使用，以改进噪声与目标图像之间的映射关系。

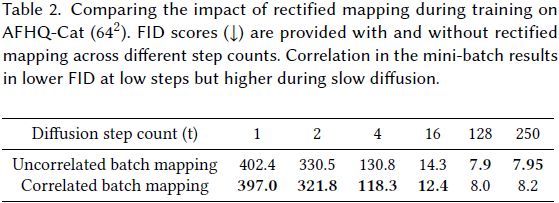
受 Rectified flow [Liu et al. 2022] 和 Instaflow [Liu et al. 2023] 的启发，可以利用相关性来矫正成对的噪声-图像。在图 5 中可视化了这种映射的改进。该图表示扩散模型的一个训练迭代。随机采样了一批成对的数据样本 x0​（红色分布）和噪声 b（蓝色分布）。先前的工作（图5(a)）在 x_0​ 和 b 之间应用了随机映射。通过在将它们输入前向过程之前应用上下文分层（图5(b)），可以改善噪声-数据映射。这种矫正的映射减小了每个噪声与其目标图像之间的距离，产生了更直接的轨迹。为了创建这种改进的映射，计算了噪声和数据之间的成对和像素间的距离。然后，对于每个 ，选择尚未使用的具有最短距离的 x0​。这种改进的映射确保在训练过程中特定图像始终与相同类型的噪声关联，从而导致跨时间步的平滑梯度流。 

4. 实验

5. 结论

我们提出了一种将相关噪声引入确定性生成扩散模型的新方法。我们的技术涉及使用基于矩阵的方法生成的不相关和相关噪声掩码的组合。通过研究不同的噪声相关性，我们揭示了噪声特性与生成图像质量之间的复杂关系。我们的发现表明，高频噪声在保留细节方面有效，但在生成低频成分方面存在困难，而低频噪声阻碍了复杂细节的生成。为了实现最佳图像质量，我们建议以一种时间相关的方式选择性地使用不同类型的噪声，利用每个噪声组分的优势。为了验证我们方法的有效性，我们在与著名方法 IADB [Heitz et al. 2023] 结合使用的同时进行了大量实验证明，通过保持训练数据和优化超参数一致，我们在各种数据集上始终观察到图像质量的显著提升。这些结果表明了我们方法在增强确定性生成扩散模型的图像生成能力方面的优越性。

未来工作。我们相信我们提出的模型将启发设计噪声模式以提高生成扩散模型效率的新研究方向。一个有趣的未来工作是将我们的模型扩展到插值超过两种噪声，以考虑更多不同类型的噪声，如低通和带通噪声。这可能为改善扩散模型的训练和采样效率提供更多自由度。此外，我们可以设计更先进的技术，在训练期间相关数据样本，这是与使用相关噪声正交的。将我们的框架（例如，时变噪声模型）扩展到 DDPM [Ho et al. 2020]、DDIM [Song et al. 2020a] 甚至潜在扩散模型 [Rombach et al. 2022] 将是另一个有趣的未来方向。通过这种方式，我们的框架可以推广到最先进的扩散模型。

在应用方面，我们在 2D 无条件和条件图像生成上测试了我们的模型。有趣的未来工作包括将我们的模型推广到合成其他数据表示，如视频和 3D 网格。