代码随想录算法训练营day11|| 20. 有效的括号、1047. 删除字符串中的所有相邻重复项、150. 逆波兰表达式求值

栈与队列part02：

20. 有效的括号

思路：

由于栈结构的特殊性，非常适合做对称匹配类的题目。

首先要弄清楚，字符串里的括号不匹配有几种情况。

一些同学，在面试中看到这种题目上来就开始写代码，然后就越写越乱。

建议在写代码之前要分析好有哪几种不匹配的情况，如果不在动手之前分析好，写出的代码也会有很多问题。

先来分析一下 这里有三种不匹配的情况，

1. 第一种情况，字符串里左方向的括号多余了 ，所以不匹配。

        2.第二种情况，括号没有多余，但是 括号的类型没有匹配上。

         3.第三种情况，字符串里右方向的括号多余了，所以不匹配。

补充一下双端队列的概念（有的解法中用到）

双端队列（Deque）
1. 概念
   双端队列（Deque）是Quene是一个子接口，双向队列是指该队列两端的元素既能入队（offer）也能出队(poll)，如果将Deque限制为只能从一端入队(push)和出队(pop)，则可限制栈的数据结构。对于栈而言，有入栈，遵循先进后出原则。

2. 双端队列的使用
   （在实际使用中，Deque接口使用的是比较多的，栈和队列都可以使用该接口，这个接口中有栈的方法，也有队列的方法）

Quene以及Deque都是继承于Collection，Deque是Quene的子接口。

public interface Deque extends Queue 

Deque也可以用作LIFO(后进先出)堆栈。 这个接口应该优先于旧的Stack类使用。 当一个队列被用作堆栈时，元素从队列的开始被推入和弹出 。堆栈方法完全等同于Deque方法。

public static void main9(String[] args) {
        //底层是一个双向链表
        Deque deque = new LinkedList<>();
        //数组实现的双端队列：底层就是一个数组
        Deque deque1 = new ArrayDeque<>();
        //顺序的双端队列也可以当作栈来使用
        Deque stack = new ArrayDeque<>();
        stack.push(1);
        stack.push(2);
        stack.push(3);//顺序的双端队列（底层是用数组来实现的）也提供了栈的相关的方法
 
    }
    public static void main8(String[] args) {
        //双端队列
        Deque deque = new LinkedList<>();
        //普通队列
        //Queue中既有offer方法，也有add方法，add在无法添加一个元素时，会抛出一个异常
        //offer方法优于add方法，如果无法添加元素，offer方法不会抛出异常
        Queue queue = new LinkedList<>();
        //链式栈  虽然是具体的类但是里面有栈的方法
        //LinkedList类中的方法是最多的，因为它实现了很多接口，此时一定会重写接口中的方法
        LinkedList stack = new LinkedList<>();
        //双向链表
        List list = new LinkedList<>();
        //其他的都是使用接口来引用的：只有接口中的方法
    }

 java版本实现代码：

class Solution {
    public boolean isValid(String s) {
        //Deque双端队列模拟栈结构来实现 
        Deque deque = new LinkedList<>(); //创建了一个双端队列 deque，用于模拟栈的行为。
        //Character表示Java中的字符数据类型，是一个包装类，用于表示一个字符对象（父类是Object）。
        char ch; //声明了一个字符变量 ch，用于存储字符串中的每个字符。
        for(int i = 0; i < s.length(); i++){
            ch = s.charAt(i); //获取字符串s中索引为 i 的字符，并赋值给变量ch
            //碰到左括号，就把相应的右括号入栈
            if(ch == '('){
                deque.push(')');
            }else if(ch ==  '['){
                deque.push(']');
            }else if(ch == '{'){
                deque.push('}');
            }else if(deque.isEmpty() || deque.peek() != ch){
            //第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号 return false
            //第二种情况：遍历字符串匹配的过程中，发现栈里没有我们要匹配的字符。所以return false
                return false;
            }else{//到这说明以上都不是了，则如果当前字符是右括号，判断是否和栈顶元素匹配
                deque.pop(); //√如果匹配，则从栈中弹出相应的括号，然后依次遍历循环比较
            }
        }

        //第一种情况：最后判断栈中是否还有未匹配的左括号，如果栈为空则返回true，否则返回false。
        return deque.isEmpty();
    }
}

注意：技巧性的东西没有固定的学习方法，还是要多看多练，自己灵活运用了。

 

 1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

• 输入："abbaca"
• 输出："ca"
• 解释：例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

思路：

本题要删除相邻相同元素，相对于20.有效的括号来说其实也是匹配问题，20. 有效的括号 是匹配左右括号，本题是匹配相邻元素，最后都是做消除的操作。

本题也是用栈来解决的经典题目。

那么栈里应该放的是什么元素呢？

我们在删除相邻重复项的时候，其实就是要知道当前遍历的这个元素，我们在前一位是不是遍历过一样数值的元素，那么如何记录前面遍历过的元素呢？

所以就是用栈来存放，那么栈的目的，就是存放遍历过的元素，当遍历当前的这个元素的时候，去栈里看一下我们是不是遍历过相同数值的相邻元素。

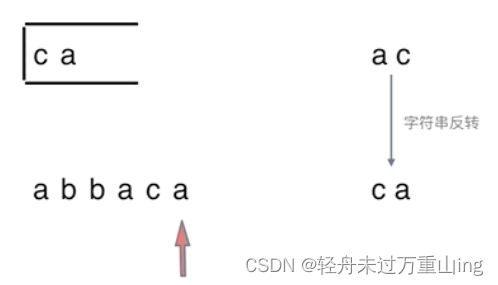
然后再去做对应的消除操作。 如动画所示：

从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以再对字符串进行反转一下，就得到了最终的结果。

class Solution {
    public String removeDuplicates(String s) {
        //方法一：使用 Deque 作为堆栈
        //ArrayDeque会比LinkedList在除了删除元素这一点外会快一点（注意）
//参考：https://stackoverflow.com/questions/6163166/why-is-arraydeque-better-than-linkedlist
        ArrayDeque deque =  new ArrayDeque<>();
        //创建了一个双端队列 deque，用于存储字符。
        char ch; //声明了一个字符变量 ch，用于存储字符串中的每个字符。
        for(int i = 0;i < s.length(); i++){ //开始循环遍历s中的每个字符 
            ch = s.charAt(i);//获取字符串 S 中索引为 i 的字符，并赋值给变量 ch。
            if(deque.isEmpty() || deque.peek() != ch){
                //如果栈为空，或者栈顶元素与当前字符不相等，则将当前字符入栈。
                deque.push(ch);
            }else{//如果栈顶元素与当前字符相等，则移除栈顶元素。
                deque.pop();
            }
        }
        String str = ""; //创建了一个空字符串str，用于存储去重后的字符。
        //栈中剩余的元素即为不重复的元素
        while(!deque.isEmpty()){
            str = deque.pop() + str; //将栈顶元素取出并拼接到字符串的前面。 eg:str1 + ", " + str2 + "!";
        }
        return str; //返回去重后的字符串。
    }
}

• 时间复杂度: O(n)
• 空间复杂度: O(n)

当然可以拿字符串直接作为栈，这样省去了栈还要转为字符串的操作。

class Solution {
    public String removeDuplicates(String s) {
        //将字符串直接 作为栈来模拟该过程
        //将res 作为栈
        // 也可以用 StringBuilder 来修改字符串，速度更快
        StringBuilder res = new StringBuilder();
        //top为 res的长度 
        int top = -1; //声明了一个整型变量 top，用于模拟栈的栈顶指针，初始值设为 -1。
        for(int i = 0; i < s.length(); i++){
            char c = s.charAt(i);
            //如果栈顶指针top >= 0,即栈中有字符时，当前字符如果和栈中字符相等，弹出栈顶元素，同时top--
            if(top >= 0 && res.charAt(top) == c){
                res.deleteCharAt(top); //删除栈顶字符，即删除StringBuilder对象res中索引为top的字符。
                top--;
            }else{
                //否则，该字符入栈，同时top ++
                res.append(c);//将当前字符追加到StringBuilder对象res的末尾。
                top++;
            }
        }
        return res.toString();//返回处理后的字符串，即StringBuilder对象res转换为字符串。
    }
}

补充一点：

在这段代码中，res 是一个 StringBuilder 对象，用于动态地构建字符串。而方法的返回类型是 String，因此需要将 StringBuilder 对象转换为 String 类型才能返回给调用者。

StringBuilder 类提供了 toString() 方法，可以将其内部的字符序列转换为一个字符串对象。因此，在方法的最后使用 res.toString() 就是将 StringBuilder 对象 res 中的字符序列转换为字符串，并将其返回给调用者。

题外话

这道题目就像是我们玩过的游戏对对碰，如果相同的元素挨在一起就要消除。

可能我们在玩游戏的时候感觉理所当然应该消除，但程序又怎么知道该如何消除呢，特别是消除之后又有新的元素可能挨在一起。

此时游戏的后端逻辑就可以用一个栈来实现（我没有实际考察对对碰或者爱消除游戏的代码实现，仅从原理上进行推断）。

游戏开发可能使用栈结构，编程语言的一些功能实现也会使用栈结构，实现函数递归调用就需要栈，但不是每种编程语言都支持递归，例如：

递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

相信大家应该遇到过一种错误就是栈溢出，系统输出的异常是Segmentation fault（当然不是所有的Segmentation fault 都是栈溢出导致的） ，如果你使用了递归，就要想一想是不是无限递归了，那么系统调用栈就会溢出。

而且在企业项目开发中，尽量不要使用递归！在项目比较大的时候，由于参数多，全局变量等等，使用递归很容易判断不充分return的条件，非常容易无限递归（或者递归层级过深），造成栈溢出错误（这种问题还不好排查！）

 150. 逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。

有效的运算符包括 + ,  - ,  * ,  / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

说明：整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

逆波兰表达式：是一种后缀表达式，所谓后缀就是指运算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。

该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。

• 适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。

所以栈与递归之间在某种程度上是可以转换的！ 这一点我们在后续讲解二叉树的时候，会更详细的讲解到。

那么来看一下本题，其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。

但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了，就可以了。

在进一步看，本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这岂不就是一个相邻字符串消除的过程，和1047.删除字符串中的所有相邻重复项 (opens new window)中的对对碰游戏是不是就非常像了。

class Solution {
    public int evalRPN(String[] tokens) {//字符串数组 tokens
        //还是用Deque来作为栈
        Deque stack = new LinkedList();//创建了一个整型双端队列 stack，用作栈。
        for(String s : tokens ){//开始一个增强型 for 循环，遍历输入的字符串数组 tokens 中的每个元素。
            if("+".equals(s)){ //leetcode内置jdk的问题，不能使用==判断字符串是否相等
            //弹出栈顶的两个元素，进行加法运算后将结果压入栈中。
                stack.push(stack.pop() + stack.pop());  // 注意 - 和/ 需要特殊处理
            }else if("-".equals(s)){
                stack.push(-stack.pop() + stack.pop());  //这里要注意后出栈的对先出栈的做 减法（除法也一样）
            }else if("*".equals(s)){
                stack.push(stack.pop() * stack.pop());
            }else if("/".equals(s)){
                //首先弹出栈顶的两个元素，并分别保存到变量 temp1 和 temp2 中。
                int temp1 = stack.pop();
                int temp2 = stack.pop();
                stack.push(temp2 / temp1);
            }else{
                //如果遍历到 数字的话，字符串转整型 并压入栈中
                stack.push(Integer.valueOf(s)); //将当前字符串转换为整型数值，并将其压入栈中
            }
        }
        return stack.pop();//返回栈顶元素，即为逆波兰表达式的最终计算结果
    }
}

• 时间复杂度: O(n)
• 空间复杂度: O(n)