【第188周周赛】异或三元数组,收集苹果,切披萨的方案数
2020/05/10 第188周周赛
第二题
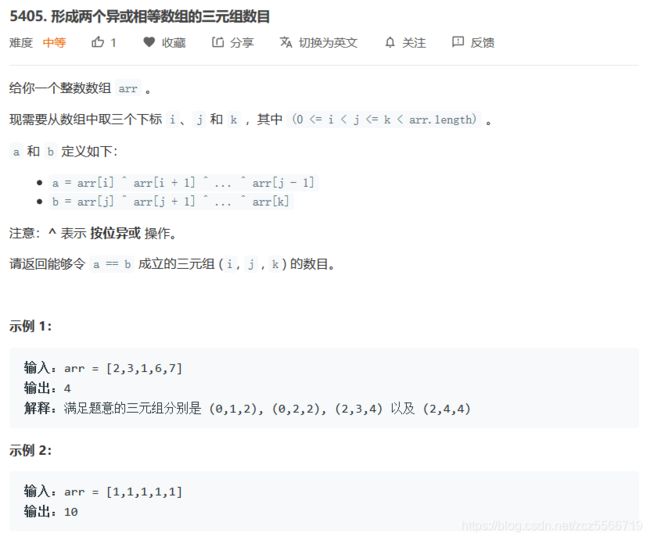
确实想到了前缀和的思路,但是没有对问题更加进一步的剖析。题目要求a==b其实相当于要求了arr[i]^...^arr[k] == 0并且对于[i,k]区间中任意拆分都可,也就是j可以在其中任取。
因为我们可以实现时间复杂度为 O ( n 2 ) O(n^2) O(n2)的方法。每次记录起点i,去寻找终点k。
class Solution:
def countTriplets(self, arr: List[int]) -> int:
## 利用了异或的特性,类似前缀和的思路。
## 如果[a,b]的异或和为0,则在之间任意拆分为两个子区间的异或和相等
## 但是尝试利用传统的前缀和失败了
n = len(arr)
ans = 0
for i in range(n):
temp = arr[i]
for j in range(i+1,n):
temp ^= arr[j]
if temp == 0:
ans += j-i
return ans
另外一种更为巧妙的方法是可以将时间复杂度降低为 O ( n ) O(n) O(n)。我们借助两个哈希表实现。
对于异或的前缀和,有一些有趣的性质:有presum(k) = arr[0]^arr[1]^...^arr[k]
arr[i]^arr[i+1]^...^arr[k] = presum(k) ^ presum(i-1)
前一种方法已经给出,只要满足 arr[i]^...arr[k]就相当于与a==b,换句话说,其实就是满足presum(k) == presum(i-1)即可。并且可以贡献k-i个合理的答案。
如果有多个一样的前缀和,不难得到,合理的答案有(k-i1)+(k-i2).... = k*num_k-sum(i)这么多个,其中,sum(i)表示对应的坐标和。因此利用两个哈希数组,prenum统计该前缀和出现的次数,preindex统计出现前缀和的坐标和。
class Solution:
def countTriplets(self, arr: List[int]) -> int:
# 复杂度为n的算法
# 如果presum(k) == prisum(i-1), 相当于贡献了k-i个(为什么是k-i?因为需要中间有个j)
# 前缀和0的情况注意考虑开头,如[2,2]显然出现了0,但是此前是没有0的。因此00的个数应该天然多1
# (k-i1)+(k-i2).... = k*num_k-sum(i)
n = len(arr)
ans = 0
dic_num = collections.defaultdict(int)
dic_index = collections.defaultdict(int)
# 考虑0的特殊情况,什么都不添加
dic_index[0] = 0
dic_num[0] = 1
cur = 0
for i in range(n):
cur ^= arr[i]
if cur in dic_num:
ans += i*dic_num[cur]-dic_index[cur]
dic_num[cur] += 1
# 这里要加一是因为这里是头索引的坐标,对应前面的k-i
dic_index[cur] += i+1
return ans
第三题
题目有一点小小的bug,没有说0是不是根节点。实际上对于一棵无向树,只要满足不出现环就可。未必是二叉等等。
我们先假设0是根节点,题目可以演变为苹果出发去找根。因为题目中给出的边,都是从根指向叶的。
class Solution(object):
def minTime(self, n, edges, hasApple):
# 从苹果出发去找根 ,但是这种方法存在一个假设就是需要0必须是根节点
dic = collections.defaultdict()
for x,y in edges:
dic[y] = x
ans = 0
visit = set([i for i in range(len(hasApple))])
for i in range(len(hasApple)):
if hasApple[i]:
index = i
while index != 0 and index in visit:
visit.remove(index)
index = dic[index]
ans += 1
return ans*2
其实这种方法有点摸鱼。
最典型的和经典的方法还是分析题目,我们需要的最短路径一定是存在苹果的道路上的。因此我们先要统计那些道路是我们需要统计的,也就是我们需要整个走一遍全树,找到(当前节点是苹果or子树存在苹果的)
然后再次对这些需要统计路径的节点进行dfs,统计路径。
class Solution:
def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
dic = collections.defaultdict(set)
for x,y in edges:
dic[x].add(y)
dic[y].add(x)
self.ans = 0
def dfs1(index, fa): # 判断有没有苹果在子树中,否则在统计中不需要搜索
for son in dic[index]:
# 注意子节点和父节点不能一样
if son != fa:
dfs1(son, index)
hasApple[index] = hasApple[son] or hasApple[index]
def dfs2(index, fa): # 统计路径
for son in dic[index]:
if son != fa and hasApple[son]:
# 对于int类型,需要定义为全局变量
self.ans += 1
dfs2(son, index)
dfs1(0, -1)
dfs2(0, -1)
return self.ans*2
注意:在代码中有一些细节
- 首先是每次进行dfs时,传入了父节点,这样可以避免在dfs中循环,在第一次循环时,就令父节点为-1
- 其次时,ans需要定义为全局变量,不然会被替代。
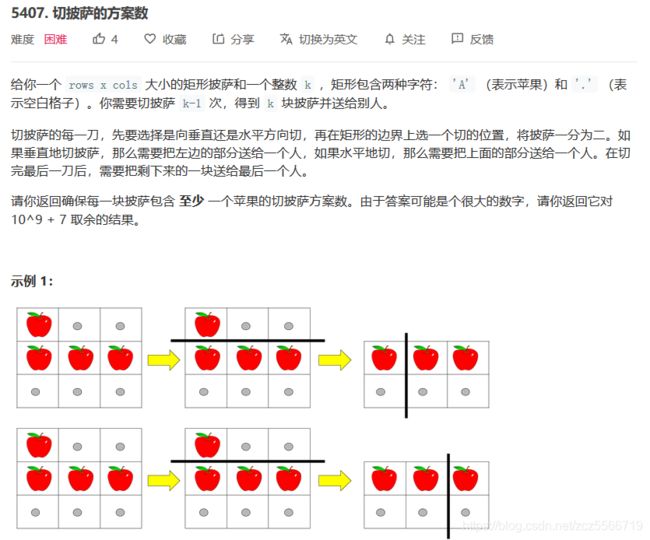
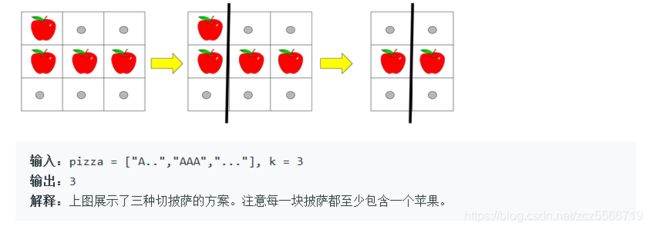
第四题
也是一道dp的题目。对于dp的问题都要主要如何寻找子问题,要求是让子问题实现无后效性,也就是之前做出的选择对当前的状态不造成影响。
因此定义子问题是右下角的矩阵,dp[i][j][rest]表示第i行第j列还剩下rest人需要披萨。同时我们需要计算出来当前剩下的披萨的苹果个数sumapple[i][j],这里可以暴力方法,也可以二维前缀和。
解题思路
- 变量定义
- 辅助数组
nums[m][n]:nums[i][j]表示pizza[i:][j:]的苹果总数 - 数组
dp[m][n][k]:dp[i][j][p]表示将pizza[i:][j:]切p刀的方案数。最终需要返回dp[0][0][k-1]
- 算法流程:
- step1:第一次遍历,计算出
nums[m][n]。计算二维前缀和 - step2:第二次遍历,计算出
dp[m][n][k]。遍历依旧是从右下到左上,递推关系式:dp[i][j][p]=Σdp[x][j][p−1]+Σdp[i][y][p−1]
-
如果横着切,设切在x行: 条件是切出来的有苹果,即
nums[i][j]−nums[x][j]>0,那么方案数dp[i][j][p]+=Σdp[x][j][p−1] -
如果竖着切,设切在y列: 条件是切出来的有苹果,即
nums[i][j]−nums[i][y]>0,那么方案数dp[i][j][p]+=Σdp[i][y][p−1] -
时间复杂度: O ( m n k ( m + n ) ) O(mnk(m+n)) O(mnk(m+n));空间复杂度: O ( m n k ) O(mnk) O(mnk)
自下而上
class Solution:
def ways(self, pizza: List[str], k: int) -> int:
mod = 10**9 + 7
m, n = len(pizza), len(pizza[0])
# dp[m][n][k]
dp = [[[0] * k for j in range(n)] for i in range(m)]
# nums[i][j]: how many apples in pizza[i:][j:]
nums = [[False] * n for i in range(m)]
for i in range(m-1, -1, -1):
for j in range(n - 1, -1, -1):
hasApple = pizza[i][j] == "A"
if i == m - 1 and j == n - 1:
nums[i][j] = hasApple
elif i == m - 1:
nums[i][j] = hasApple + nums[i][j + 1]
elif j == n - 1:
nums[i][j] = hasApple + nums[i + 1][j]
else:
nums[i][j] = hasApple + nums[i + 1][j] + nums[i][j + 1] - nums[i + 1][j + 1]
# dp[i][j][p] = sum(dp[x][j][p] for x in [i+1,m-1]) + sum(dp[i][y][p] for y in [j+1, n-1])
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
# 给出dp的初始状态
if nums[i][j]:
dp[i][j][0] = 1
# 从最小的子问题开始,只需要再切一刀
for p in range(1, k):
for x in range(i+1, m):
if nums[i][j] > nums[x][j]:
dp[i][j][p] += dp[x][j][p-1] % mod
for y in range(j+1, n):
if nums[i][j] > nums[i][y]:
dp[i][j][p] += dp[i][y][p-1] % mod
return dp[0][0][k-1] % mod
带memo的
class Solution:
def ways(self, pizza: List[str], k: int) -> int:
n = len(pizza)
m = len(pizza[0])
MOD = 10**9+7
dp = [[[-1]*(k+1) for _ in range(m)] for _ in range(n)]
sumapple = [[0]*m for _ in range(n)]
def dfs(i, j, rest):
if dp[i][j][rest] != -1:
return dp[i][j][rest]
if sumapple[i][j]<rest:
dp[i][j][rest] = 0
return dp[i][j][rest]
if rest == 1:
#dp[i][j][rest] = 1
return 1
# 开始切割
dp[i][j][rest] = 0
for k in range(i+1,n):
if sumapple[k][j] < sumapple[i][j]:
dp[i][j][rest] += dfs(k, j, rest-1)
dp[i][j][rest] %= MOD
for k in range(j+1, m):
if sumapple[i][k] < sumapple[i][j]:
dp[i][j][rest] += dfs(i, k, rest-1)
dp[i][j][rest] %= MOD
return dp[i][j][rest]
for i in range(n-1,-1,-1):
for j in range(m-1,-1,-1):
if pizza[i][j] == 'A':
ap = 1
else:
ap = 0
if i == n-1 and j == m-1:
sumapple[i][j] = ap
elif i == n-1:
sumapple[i][j] = ap+sumapple[i][j+1]
elif j == m-1:
sumapple[i][j] = ap+sumapple[i+1][j]
else:
sumapple[i][j] = sumapple[i+1][j]+sumapple[i][j+1]-sumapple[i+1][j+1]+ap
return dfs(0,0,k)
代码中计算二维前缀和的方法也值得学习一下。
以上就是全部内容,真的有点难啊,估计我三道题都要跪。哭了