【Leetcode】优先队列（PriorityQueue）问题解析

优先队列PriorityQueue对应的堆是一种常用的数据结构。

优先队列PriorityQueue

1. 简介

Java PriorityQueue 实现了 Queue 接口，不允许放入 null 元素；其通过堆实现，具体说是通过完全二叉树（complete binary tree）实现的小顶堆（任意一个非叶子节点的权值，都不大于其左右子节点的权值），也就意味着可以通过数组来作为PriorityQueue 的底层实现，数组初始大小为11；也可以用一棵完全二叉树表示。

2. java内置优先队列的API

PriorityQueue queue = new PriorityQueue(new Comparator<Integer>() {
	  @Override
	    public int compare(Integer o1, Integer o2) {
	        return o1 - o2;
	    }
	});

Lambda表达式写法(推荐使用)

PriorityQueue<Integer> queue = new PriorityQueue<>((o1 , o2) -> o1 - o2); // 小根堆
PriorityQueue<Integer> queue = new PriorityQueue<>((o1 , o2) -> o2 - o1); // 大根堆

23. 合并K个升序链表

1. 题目描述

leetcode题目链接：23. 合并K个升序链表

2. 思路分析

将链表存入优先队列中，使用优先队列来选择最小元素，先把k个链表加入到优先队列中，然后依次从队列中取出链表，把链表的节点插入小根堆中。

3. 参考代码

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }
        // 小根堆
        PriorityQueue<ListNode> queue = new PriorityQueue<>((o1, o2) -> (o1.val - o2.val));
        for (ListNode list : lists) {
            if (list != null) {
                queue.offer(list);
            }
        }
        ListNode dummy = new ListNode(-1);  // 头结点
        ListNode cur = dummy;
        while (!queue.isEmpty()) {
            ListNode head = queue.poll();
            cur.next = head;
            if (head.next != null) {
                queue.offer(head.next);
            }
            cur = cur.next;
        }
        return dummy.next;
    }
}

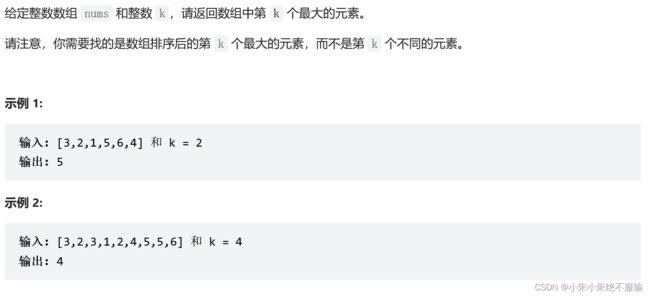
215. 数组中的第K个最大元素

1. 题目描述

leetcode题目链接：215. 数组中的第K个最大元素

2. 思路分析

优先队列：小根堆存储元素，判断当堆中元素多于k个时，删除堆顶元素。 最后堆顶元素即为第k个最大元素。

3. 参考代码

class Solution {
    public int findKthLargest(int[] nums, int k) {
        // 小根堆
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int num : nums) {
            queue.offer(num);
            // 堆中元素多于k个时，删除堆顶元素
            if (queue.size() > k) {
                queue.poll();
            }
        }
        return queue.peek();  // 堆顶元素即为第k个最大元素
    }
}

1753. 移除石子的最大得分

1. 题目描述

leetcode题目链接：1753. 移除石子的最大得分

2. 思路分析

方法一：排序

当排序后的第一个数或者第二个数大于0的时候，将第一个数和第二个数分别减1，得分加1，重新对数组进行排序。

方法二：优先队列

大根堆，第一个poll()就是最大的，第二个poll()的就是中间的，判断当中间的值不等于0，分数加1，再把最大值和中间值各自减一加入大根堆。

3. 参考代码

方法一：排序

class Solution {
    public int maximumScore(int a, int b, int c) {
        // 排序
        int[] nums = new int[]{a, b, c};
        Arrays.sort(nums);
        int res = 0;
        while (nums[0] > 0 || nums[1] > 0) {
            nums[1]--;
            nums[2]--;
            res++;
            Arrays.sort(nums);
        }
        return res;
    }
}

方法二：优先队列

class Solution {
    public int maximumScore(int a, int b, int c) {
        // 大根堆
        PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2) -> o2 - o1);
        queue.offer(a);
        queue.offer(b);
        queue.offer(c);
        int res = 0;
        while(true) {
            int max = queue.poll();
            int mid = queue.poll();
            if (mid == 0) break;
            res++;
            queue.offer(mid - 1);
            queue.offer(max - 1);
        }
        return res;
    }
}

LCP 30. 魔塔游戏

1. 题目描述

leetcode题目链接：LCP 30. 魔塔游戏

2. 思路分析

贪心算法加优先队列，当血不够减时，把扣的最多的血加回来，再把扣的最多的血调整数组末尾。优先队列用来存储扣的血，小根堆，每次输出的都是扣的最多的血。

3. 参考代码

class Solution {
    public int magicTower(int[] nums) {
        // 贪心算法加优先队列，每次不够用的时候，将负的最小值调整到序列末尾
        int sum = Arrays.stream(nums).sum();
        sum = sum + 1;
        if (sum < 1) return -1;
        long blood = 1;  // 防止溢出
        int count = 0;
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int num : nums) {
            blood += num;
            if (num < 0) queue.offer(num);
            if (blood < 1) {
                while (blood < 1 && !queue.isEmpty()) {
                    blood -= queue.poll();  // 加上减去的最小值，将最小值调整到末尾
                    count++;
                }
            }
        }
        return count;
    }
}

1705. 吃苹果的最大数目

1. 题目描述

leetcode题目链接：1705. 吃苹果的最大数目

2. 思路分析

优先队列，按第i天的苹果可以存储到的天数和第i天长出的苹果个数，构建小根堆。如果时间到了，且没有处在保质期的苹果，则break。然后移除超过保质期的苹果，最后吃苹果。

3. 参考代码

class Solution {
    public int eatenApples(int[] apples, int[] days) {
        // 优先队列，按第i天的苹果可以存储到的天数和第i天长出的苹果个数，构建小根堆
        PriorityQueue<int[]> queue = new PriorityQueue<>((o1, o2) -> o1[0] - o2[0]);
        int count = 0, day = 0;
        while (true) {
            if (day < apples.length) {
                queue.offer(new int[]{days[day] + day, apples[day]});
            } else if (day >= apples.length && queue.isEmpty()) {
                break;  // 时间到了，且没有处在保质期的苹果
            }
            // 移除腐烂苹果
            while (!queue.isEmpty() && (queue.peek()[0] <= day || queue.peek()[1] == 0)) {
                queue.poll();
            }
            // 吃苹果
            if (!queue.isEmpty()) {
                count++;
                queue.peek()[1]--;
            }
            // 天数+1
            day++;
        }
        return count;
    }
}

778. 水位上升的泳池中游泳

1. 题目描述

leetcode题目链接：778. 水位上升的泳池中游泳

2. 思路分析

优先队列+BFS，从起点开始bfs扩散，看需要几步到达终点，使用优先队列选择最小的高度，res = Math.max(res, 路径中每个位置的高度)。

3. 参考代码

class Solution {
    public int swimInWater(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        boolean[][] visited = new boolean[m][n];
        int res = 0;
        int[][] dirs = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
        // 优先队列每次拿出高度最小的元素
        PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> grid[a[0]][a[1]] - grid[b[0]][b[1]]);
        queue.offer(new int[]{0, 0});  // 存储索引
        visited[0][0] = true;
        while (!queue.isEmpty()) {
            int[] index = queue.poll();
            res = Math.max(res, grid[index[0]][index[1]]);
            if (index[0] == m - 1 && index[1] == n - 1) {
                return res;
            }
            for (int[] dir : dirs) {
                int x = index[0] + dir[0];
                int y = index[1] + dir[1];
                if (x < 0 || y < 0 || x >= m || y >= n || visited[x][y]) {
                    continue;
                }
                queue.offer(new int[]{x, y});
                visited[x][y] = true;
            }
        }
        return -1;
    }
}