经典排序算法
经典排序算法
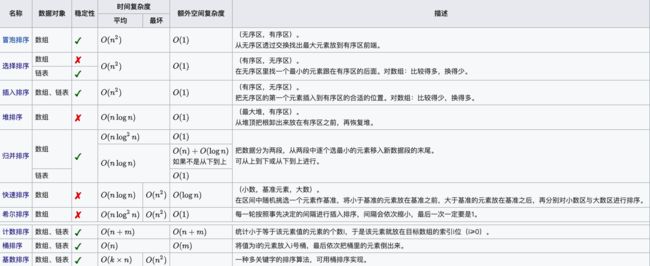
- 概述
- 一、时间复杂度 O(n^2) 级排序算法
-
- 1、冒泡排序(重要)
- 2、选择排序
- 3、插入排序
- 二、时间复杂度 O(nlogn) 级排序算法
-
- 1、希尔排序
- 2、堆排序(重要)
- 3、快速排序(重要)
- 4、归并排序(重要)
- 三、时间复杂度 O(n) 级排序算法
-
- 1、计数排序(重要)
- 2、基数排序
- 3、桶排序
概述
- 全部排序算法记忆口诀:
- 选泡插:选择排序、冒泡排序、插入排序
- 快归希堆:快速排序、归并排序、希尔排序、堆排序
- 桶计基:桶排序、计数排序、基数排序
- 稳定与不稳定常用排序算法记忆口诀:
- 稳定:冒 - 插 - 归
- 不稳定:快 - 选 - 堆
- 什么是稳定排序、原地排序?
稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 仍然在 b 的前面,则为:稳定排序。非稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为:非稳定排序。原地排序:在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。非原地排序:需要利用额外的数组来辅助排序。
一、时间复杂度 O(n^2) 级排序算法
1、冒泡排序(重要)
-
通常来说,冒泡排序有两种写法:
写法一:一边比较一边向后两两交换,将最大值 / 最小值冒泡到最后一位;
写法二(经过优化的写法):使用一个变量记录当前轮次的比较是否发生过交换,如果没有发生交换表示已经有序,不再继续排序; -
写法一:
void bubbleSort(vector<int>& a, int n) { for (int i = 0; i < n - 1 ; ++i) { // 对于数组a的前n个元素,排序n - 1轮 for (int j = 0; j < n - 1 - i; ++j) { // 每一轮分别进行n - 1、n - 2...1(= n - 1 - i)次循环 if (a[j] < a[j + 1]) // 降序!若改为升序,则:a[j] > a[j + 1] swap(a[j], a[j + 1]); } } }最外层的 for 循环每经过一轮,剩余数字中的最大值就会被移动到当前轮次的最后一位,中途也会有一些相邻的数字经过交换变得有序。总共比较次数是 :
(n-1)+(n-2)+(n-3)+…+1。
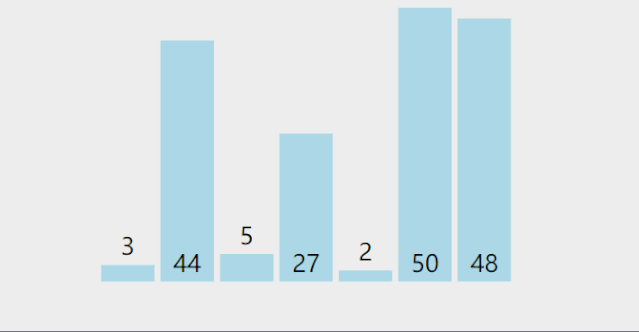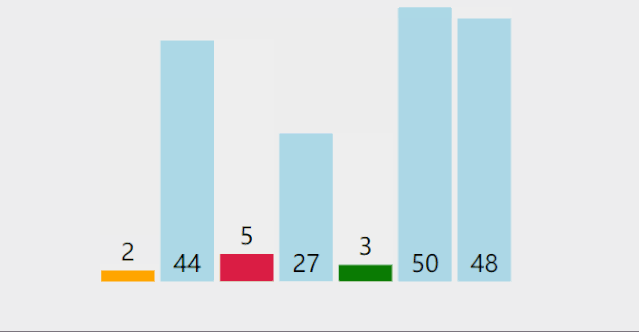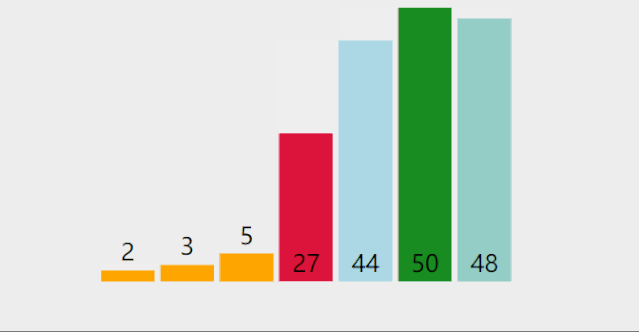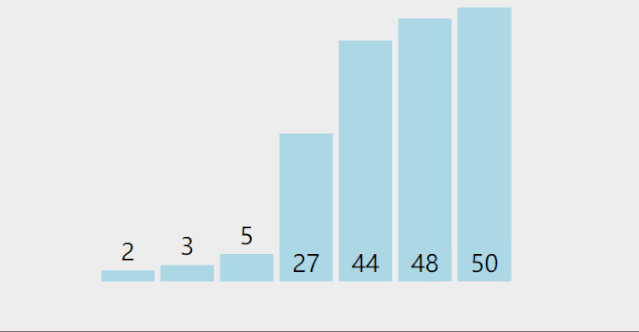
这种写法相当于相邻的数字两两比较,并且规定:“谁大谁站右边”。经过n-1轮,数字就从小到大排序完成了。整个过程看起来就像一个个气泡不断上浮,这也是“冒泡排序法”名字的由来。 -
写法二(经过优化的写法):
void bubbleSort(vector<int>& a) { int n = a.size(); bool flag = false; for (int i = 0; i < n - 1; ++i) { // 对于数组a的共n个元素,排序n - 1轮 flag = false; for (int j = 0; j < n - 1 - i; ++j) { if (a[j] > a[j + 1]) { // 某一趟排序中,只要发生一次元素交换,flag就从false变为了true // 也即表示这一趟排序还不能确定所剩待排序列是否已经有序,应继续下一趟循环 flag = true; swap(a[j], a[j + 1]); } } // 但若某一趟中一次元素交换都没有,即依然为flag = false,那么表明所剩待排序列已经有序 // 之后就不必再进行趟数比较,外层循环应该结束,即此时if (!flag) break; 跳出循环 if (!flag) { break; } } }最外层的 for 循环每经过一轮,剩余数字中的最大值仍然是被移动到当前轮次的最后一位。这种写法相对于第一种写法的优点是:如果一轮比较中没有发生过交换,则立即停止排序,因为此时剩余数字一定已经有序了。
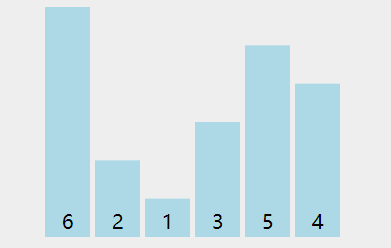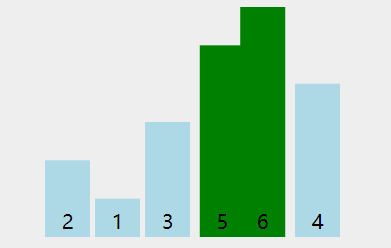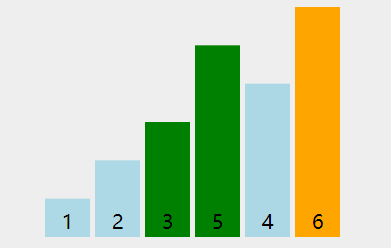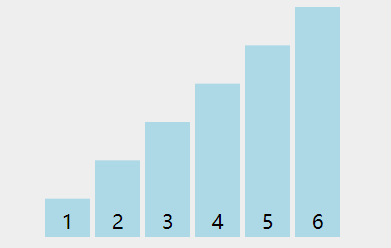
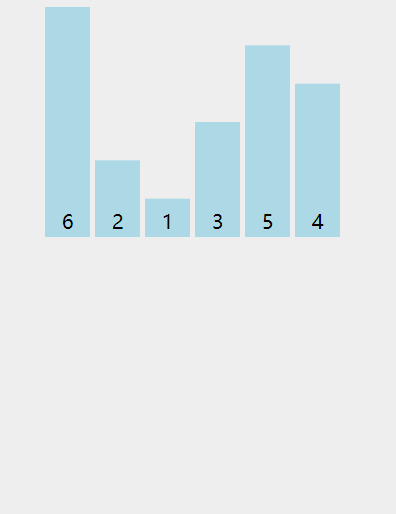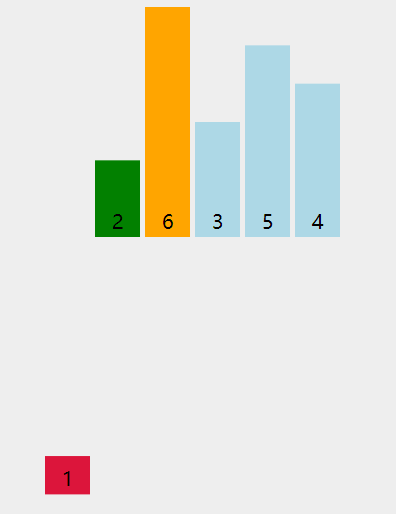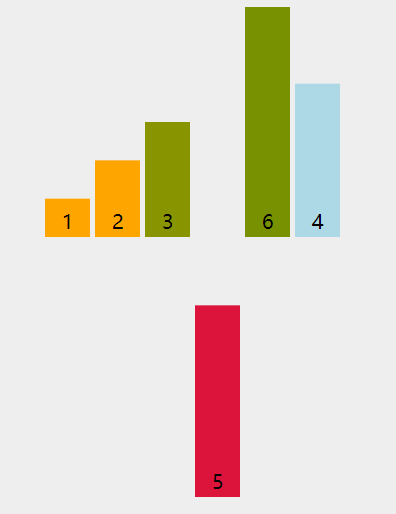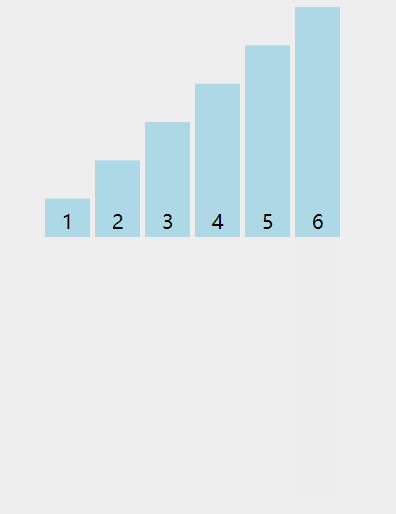
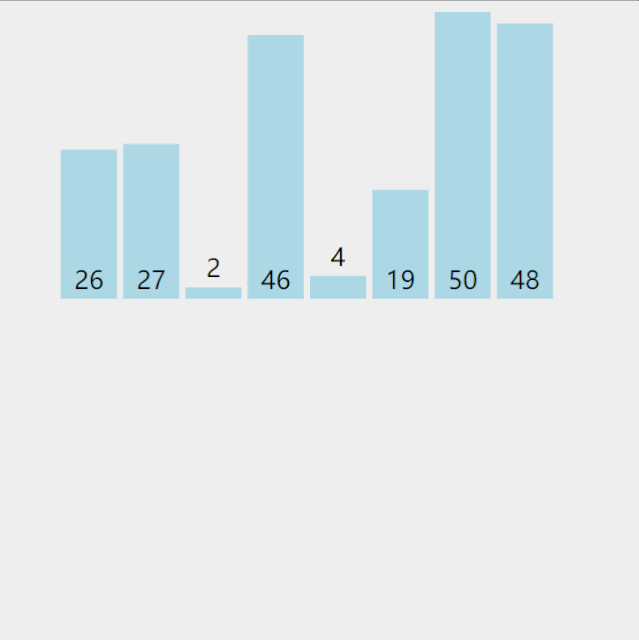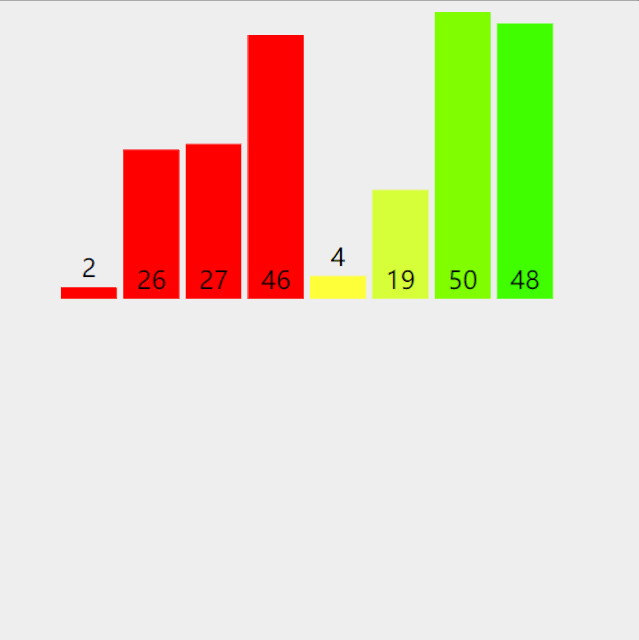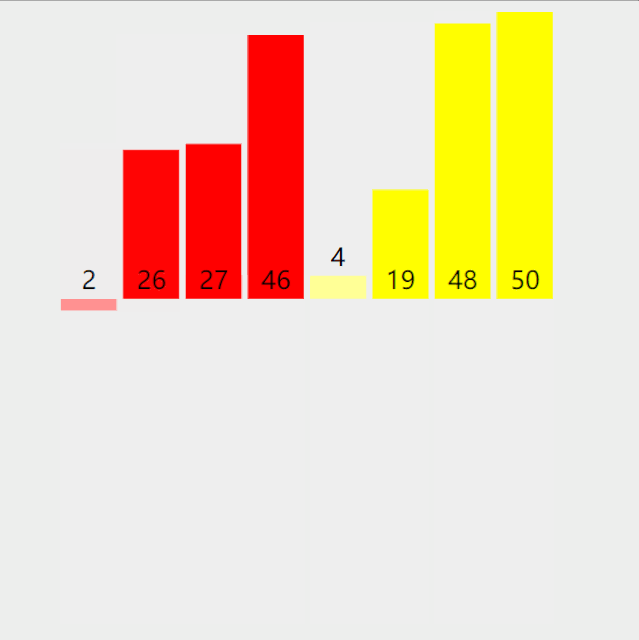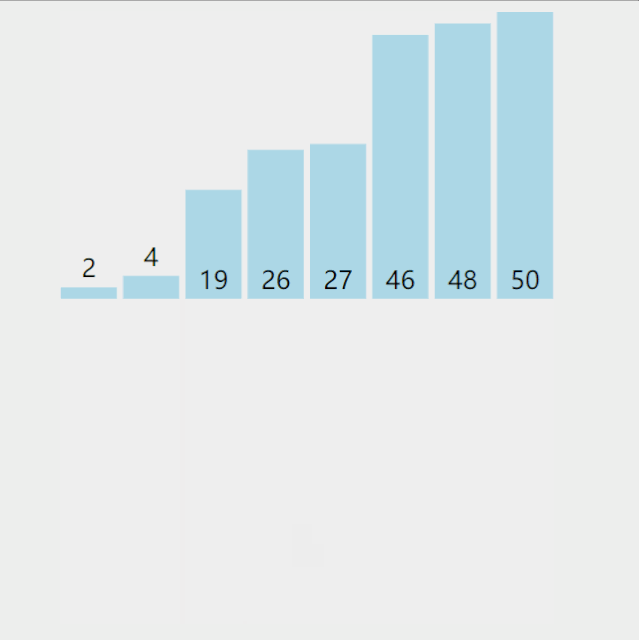
根据上动图,得到如下具体过程:
1. 第一轮排序将数字 6 移动到最右边;
2. 第二轮排序将数字 5 移动到最右边,同时中途将 1 和 2 排了序;
3. 第三轮排序时,没有发生交换,表明排序已经完成,不再继续比较。
2、选择排序
-
思想:双重循环遍历数组,每经过一轮比较,找到最小元素的下标,将其交换至首位。
-
代码如下:
void SelectionSort(vector<int>& arr) { int minIndex = 0; for (int i = 0; i < arr.size() - 1; i++) { minIndex = i; for (int j = i + 1; j < arr.size(); j++) { if (arr[minIndex] > arr[j]) { minIndex = j; // 记录最小值的下标 } } swap(arr[i], arr[minIndex]); // 将最小元素交换至首位 } } -
说明:选择排序就好比第一个数字站在擂台上,大吼一声:“还有谁比我小?”。剩余数字来挨个打擂,如果出现比第一个数字小的数,则新的擂主产生。每轮打擂结束都会找出一个最小的数,将其交换至首位。经过 n-1 轮打擂,所有的数字就按照从小到大排序完成了。
-
冒泡排序 和 选择排序 有什么不同?
答:冒泡排序在比较过程中就不断交换;而选择排序增加了一个变量保存最小值 / 最大值的下标,遍历完成后才交换,减少了交换次数。
3、插入排序
-
插入排序的思想:类比在打扑克牌时,我们一边抓牌一边给扑克牌排序,每次摸一张牌,就将它插入手上已有的牌中合适的位置,逐渐完成整个排序。
-
两种写法:
交换法:在新数字插入过程中,不断与前面的数字交换,直到找到自己合适的位置。
移动法:在新数字插入过程中,与前面的数字不断比较,前面的数字不断向后挪出位置,当新数字找到自己的位置后,插入一次即可。 -
交换法:
void InsertSort(vector<int>& arr) { // 从第二个数开始,往前插入数字 for (int i = 1; i < arr.size(); i++) { int j = i; // j 记录当前数字下标 // 当前数字比前一个数字小,则将当前数字与前一个数字交换 while (j >= 1 && arr[j] < arr[j - 1]) { swap(arr[j], arr[j - 1]); j--; // 更新当前数字下标 } } }说明:当数字少于两个时,不存在排序问题,当然也不需要插入,所以我们直接从第二个数字开始往前插入。整个过程就像是已经有一些数字坐成了一排,这时一个新的数字要加入,这个新加入的数字原本坐在这一排数字的最后一位,然后它不断地与前面的数字比较,如果前面的数字比它大,它就和前面的数字交换位置。
-
移动法:
void InsertSort(vector<int>& arr) { // 从第二个数开始,往前插入数字 for (int i = 1; i < arr.size(); i++) { int currentNumber = arr[i]; int j = i - 1; // 寻找插入位置的过程中,不断地将比 currentNumber 大的数字向后挪 while (j >= 0 && currentNumber < arr[j]) { arr[j + 1] = arr[j]; j--; } // 两种情况会跳出循环: // 1. 遇到一个小于或等于 currentNumber 的数字,跳出循环,currentNumber 就坐到它后面。 // 2. 已经走到数列头部,仍然没有遇到小于或等于 currentNumber 的数字,也会跳出循环,此时 j 等于 -1,currentNumber 就坐到数列头部。 arr[j + 1] = currentNumber; } }说明:
1. 在交换法插入排序中,每次交换数字时,swap 函数都会进行三次赋值操作。但实际上,新插入的这个数字并不一定适合与它交换的数字所在的位置。也就是说,它刚换到新的位置上不久,下一次比较后,如果又需要交换,它马上又会被换到前一个数字的位置。
2. 想到一种优化方案 - 移动法:让新插入的数字先进行比较,前面比它大的数字不断向后移动,直到找到适合这个新数字的位置后,新数字只做一次插入操作即可。
3. 整个过程就像是已经有一些数字坐成了一排,这时一个新的数字要加入,所以这一排数字不断地向后腾出位置,当新的数字找到自己合适的位置后,就可以直接坐下了。重复此过程,直到排序结束。
二、时间复杂度 O(nlogn) 级排序算法
1、希尔排序
-
希尔排序本质上是对插入排序的一种优化,它利用了插入排序的简单,又克服了插入排序每次只交换相邻两个元素的缺点。
-
希尔排序和冒泡、选择、插入等排序算法一样,逐渐被快速排序所淘汰,但作为承上启下的算法,不可否认的是,希尔排序身上始终闪耀着算法之美。
-
基本思想:
1. 将待排序数组按照一定的间隔分为多个子数组,每组分别进行插入排序。这里按照间隔分组指的不是取连续的一段数组,而是每跳跃一定间隔取一个值组成一组。
2. 逐渐缩小间隔进行下一轮排序。
3. 最后一轮时,取间隔为 1,也就相当于直接使用插入排序。但这时经过前面的「宏观调控」,数组已经基本有序了,所以此时的插入排序只需进行少量交换便可完成。 -
总结思想:采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
-
举例:对数组
[84, 83, 88, 87, 61, 50, 70, 60, 80, 99]进行希尔排序的过程如下:
第一遍(5 间隔排序):按照 间隔5 分割子数组,共分成五组,分别是[84, 50], [83, 70], [88, 60], [87, 80], [61, 99]。对它们进行插入排序,排序后它们分别变成:[50, 84], [70, 83], [60, 88], [80, 87], [61, 99],此时整个数组变成[50, 70, 60, 80, 61, 84, 83, 88, 87, 99]。
第二遍(2 间隔排序):按照 间隔 2 分割子数组,共分成两组,分别是[50, 60, 61, 83, 87], [70, 80, 84, 88, 99]。对他们进行插入排序,排序后它们分别变成:[50, 60, 61, 83, 87], [70, 80, 84, 88, 99],此时整个数组变成[50, 70, 60, 80, 61, 84, 83, 88, 87, 99]。这里有一个非常重要的性质:当我们完成 2 间隔排序后,这个数组仍然是保持 5 间隔有序的。也就是说,更小间隔的排序没有把上一步的结果变坏。
第三遍(1 间隔排序,等于直接插入排序):按照 间隔1 分割子数组,分成一组,也就是整个数组。对其进行插入排序,经过前两遍排序,数组已经基本有序了,所以这一步只需经过少量交换即可完成排序。排序后数组变成[50, 60, 61, 70, 80, 83, 84, 87, 88, 99],整个排序完成。 -
上述例子的动图演示:
-
详细介绍:https://mp.weixin.qq.com/s/4kJdzLB7qO1sES2FEW0Low
2、堆排序(重要)
-
堆排序过程如下:
1. 用数列构建出一个大顶堆,取出堆顶的数字;
2. 调整剩余的数字,构建出新的大顶堆,再次取出堆顶的数字;
3. 循环往复,完成整个排序。 -
整体的思路就是这么简单,需要解决的问题有两个:
1. 如何用数列构建出一个大顶堆;
2. 取出堆顶的数字后,如何将剩余的数字调整成新的大顶堆。 -
构建大顶堆 & 调整堆有两种方式:
方案一:将整个数列的初始状态视作一棵完全二叉树,自底向上调整树的结构,使其满足大顶堆的要求。
方案二(个人常用):从 0 开始,将每个数字依次插入堆中,一边插入,一边调整堆的结构,使其满足大顶堆的要求; -
在介绍堆排序具体实现之前,先要了解完全二叉树的几个性质。将根节点的下标视为
0,则完全二叉树有如下性质:
1. 对于完全二叉树中的第i个数,它的左子节点下标:left = 2i + 1
2. 对于完全二叉树中的第i个数,它的右子节点下标:right = left + 1
3. 对于有n个元素的完全二叉树(n ≥ 2),它的最后一个非叶子结点的下标:n/2 - 1 -
方案一的动图演示如下:
- 整体代码如下:
void heapSortSolution() {
// 1: 先将待排序的数视作完全二叉树(按层次遍历顺序进行编号, 从0开始)
vector<int> arr = { 3,4,2,1,5,8,7,6 };
heapSort(arr, arr.size());
}
void heapSort(vector<int>& arr, int len) {
// 2:完全二叉树的最后一个非叶子节点,也就是最后一个节点的父节点。
// 最后一个节点的索引为数组长度len-1,那么最后一个非叶子节点的索引应该是为(len-1-1)/2,如果其子节点的值大于其本身的值。则把他和较大子节点进行交换。
// 初次构建堆,i要从最后一个非叶子节点开始向上遍历,建立堆,所以是len / 2 - 1(or (len - 1 - 1) / 2 ),0这个位置要加等号
for (int i = len / 2 - 1; i >= 0; i--) { // 解决第 1 个问题
adjust(arr, i, len);
}
// 从最后一个元素的下标开始往前遍历,每次将堆顶元素交换至当前位置,并且缩小长度(i为长度),从0处开始adjust
for (int i = len - 1; i > 0; i--) { // 解决第 2 个问题
swap(arr[0], arr[i]);
adjust(arr, 0, i); // 注意每次adjust是从根往下调整,所以这里index是0!因为每交换一次之后,就把最大值拿出(不再参与调整堆),第二个参数应该写i而不是length
}
}
// 方案一:
void adjust(vector<int>& arr, int index, int len) {
int maxid = index; // 初始化,假设左右孩子的双亲节点就是最大值
// 计算左右子节点的下标 left = 2 * i + 1 right = 2 * i + 2 parent = (i - 1) / 2
int left = 2 * index + 1, right = 2 * index + 2;
// 寻找当前以index为根的子树中最大/最小的元素的下标
// 降序!!!
if (left < len and arr[left] < arr[maxid]) {
maxid = left;
}
if (right < len and arr[right] < arr[maxid]) {
maxid = right;
}
// 升序!!!
/*if (left < len and arr[left] > arr[maxid]) {
maxid = left;
}
if (right < len and arr[right] > arr[maxid]) {
maxid = right;
}*/
// 进行交换,记得要递归进行adjust,传入的index是maxid
if (maxid != index) {
swap(arr[maxid], arr[index]);
adjust(arr, maxid, len); //递归,使其子树也为堆
}
}
// 方案二:构建【大顶堆】时的下沉sink操作 ——> 堆排序结果【升序】!!!
// --- 若修改为:(1)、(2)就是构建【小顶堆】的下沉sink操作 ——> 堆排序结果【降序】!!!
void adjust(vector<int>& arr, int start, int end) { // 依据之前构建【大顶堆】的方法,进行相应的下沉操作
int parent = start;
while (parent * 2 + 1 < end) {
int son = parent * 2 + 1;
if (son + 1 < end && arr[son] < arr[son + 1]) { // 改为:arr[son] > arr[son + 1] --- (1)
son++;
}
if (arr[parent] >= arr[son]) { // 改为:arr[parent] <= arr[son] --- (2)
return;
}
else {
swap(arr[parent], arr[son]);
}
parent = son;
}
}
-
方案一:我们将数组视作一颗完全二叉树,从它的最后一个非叶子结点开始,调整此结点和其左右子树,使这三个数字构成一个大顶堆。调整过程由
adjust函数处理,adjust函数记录了最大值的下标,根结点和其左右子树结点在经过比较之后,将最大值交换到根结点位置。这样,这三个数字就构成了一个大顶堆。需要注意的是:如果根结点和左右子树结点任何一个数字发生了交换,则还需要保证调整后的子树仍然是大顶堆,所以子树会执行一个递归的调整过程。- 这里的递归比较难理解,打个比方:构建大顶堆的过程就是一堆数字比赛谁更大。比赛过程分为初赛、复赛、决赛,每场比赛都是三人参加。但不是所有人都会参加初赛,只有叶子结点和第一批非叶子结点会进行三人组初赛。初赛的冠军站到三人组的根结点位置,然后继续参加后面的复赛。
- 而有的人生来就在上层,比如李小胖,它出生在数列的第一个位置上,是二叉树的根结点,当其他结点进行初赛、复赛时,它就静静躺在根结点的位置等一场决赛。
- 当王大强和张壮壮,经历了重重比拼来到了李小胖的左右子树结点位置。他们三个人开始决赛。王大强和张壮壮是靠实打实的实力打上来的,他们已经确认过自己是小组最强。而李小胖之前一直躺在这里等决赛。如果李小胖赢了他们两个,说明李小胖是所有小组里最强的,毋庸置疑,他可以继续坐在冠军宝座。
- 但李小胖如果输给了其中任何一个人,比如输给了王大强。王大强会和张壮壮对决,选出本次构建大顶堆的冠军。但李小胖能够坐享其成获得第三名吗?生活中或许会有这样的黑幕,但程序不会欺骗我们。李小胖跌落神坛之后,就要从王大强的打拼路线回去,继续向下比较,找到自己真正实力所在的真实位置。这就是
adjust中会继续递归调用adjust的原因。 - 当构建出大顶堆之后,就要把冠军交换到数列最后,深藏功与名。来到冠军宝座的新人又要和李小胖一样,开始向下比较,找到自己的真实位置,使得剩下的
n - 1个数字构建成新的大顶堆。这就是heapSort方法的for循环中,调用adjust的原因。 - 变量
len用来记录还剩下多少个数字没有排序完成,每当交换了一个堆顶的数字,len就会减1。在adjust方法中,使用len来限制剩下的选手,不要和已经躺在数组最后,当过冠军的人比较,免得被暴揍。
-
方案二: 核心:构建大顶堆时的下沉 sink 操作 ——> 另一篇文章:核心算法模板
3、快速排序(重要)
-
经典总结:快速排序是先将一个元素排好序,然后再将剩下的元素排好序。——> 二叉树遍历时的前序位置处理。
-
从二叉树的视角,我们可以把子数组
nums[lo..hi]理解成二叉树节点上的值,srot函数理解成二叉树的遍历函数。
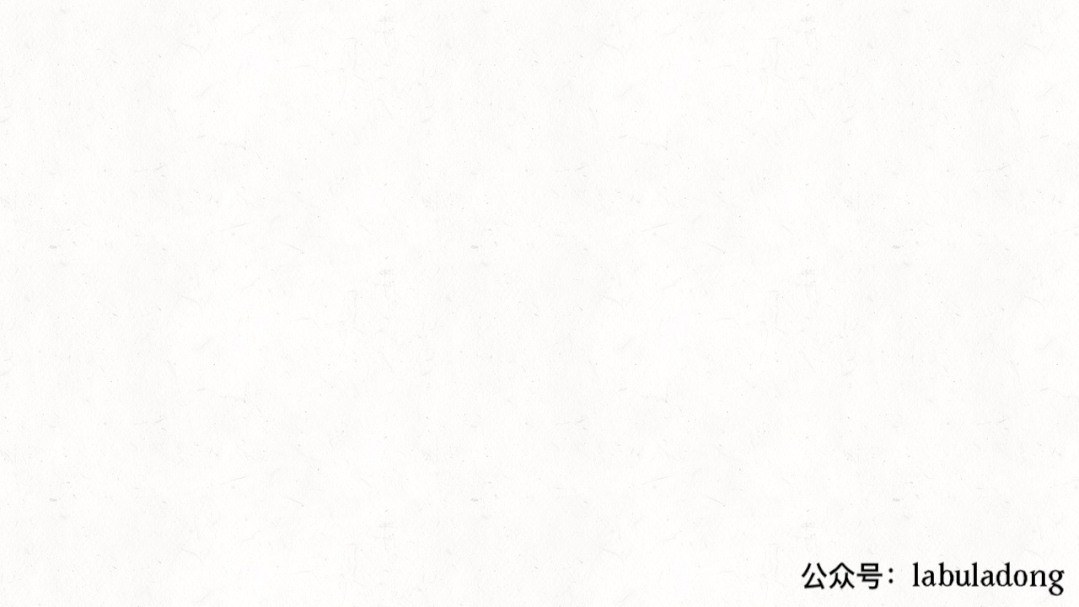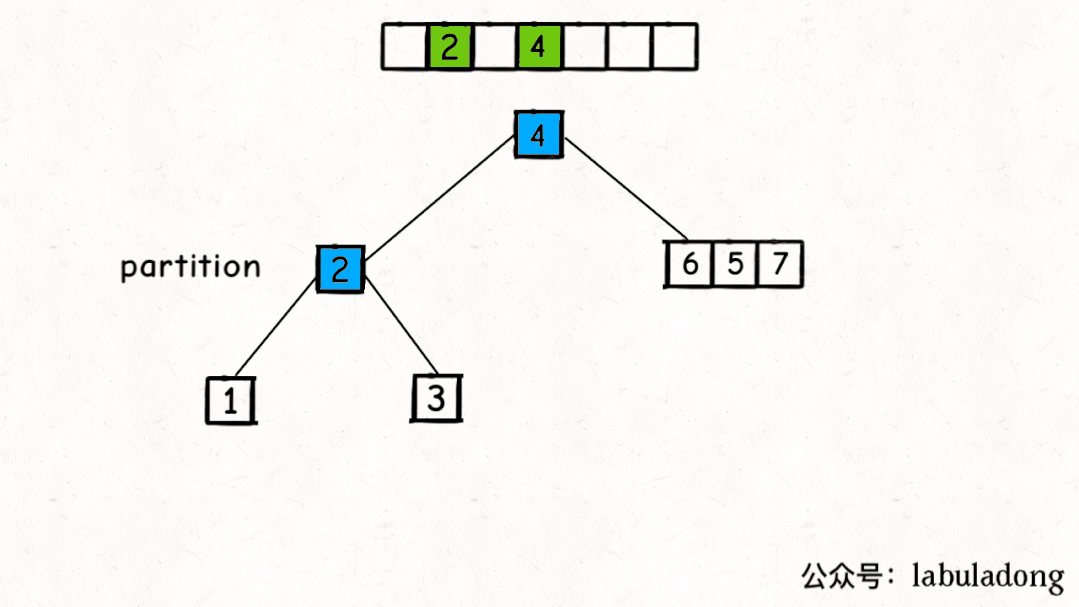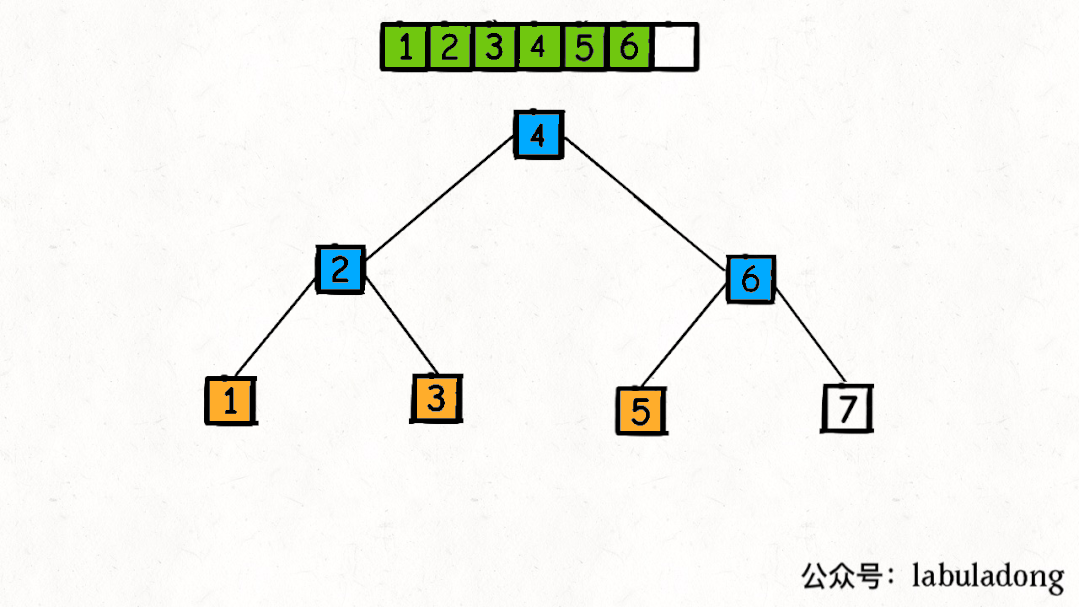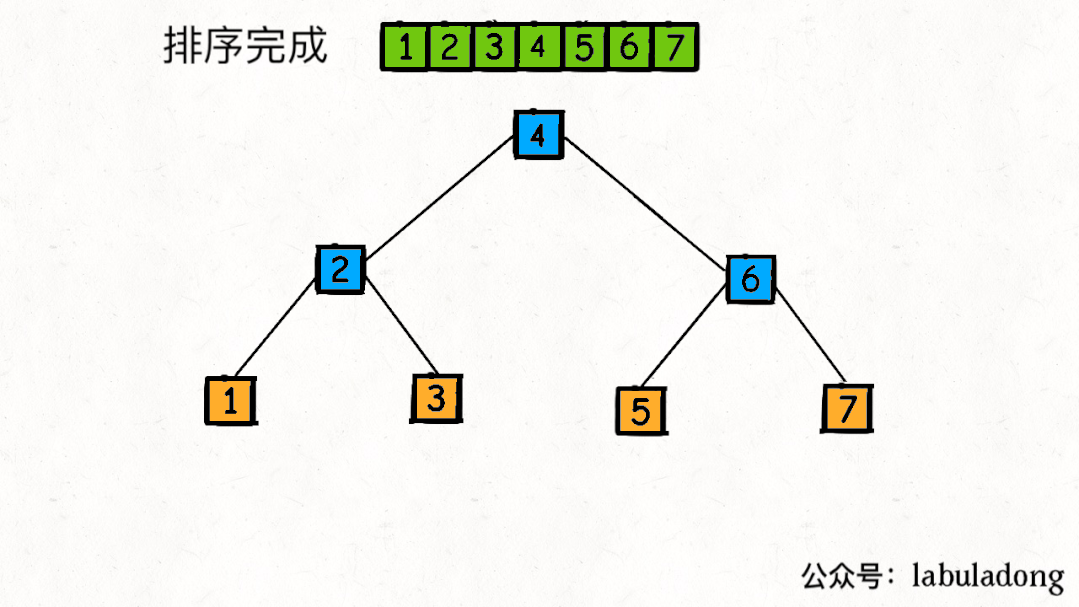
因为 partition 函数每次都将数组切分成左小右大的两部分,最后形成的是一棵 二叉搜索树(BST) !快速排序的过程是一个构造【二叉搜索树】的过程。
-
动图演示:
-
代码框架:
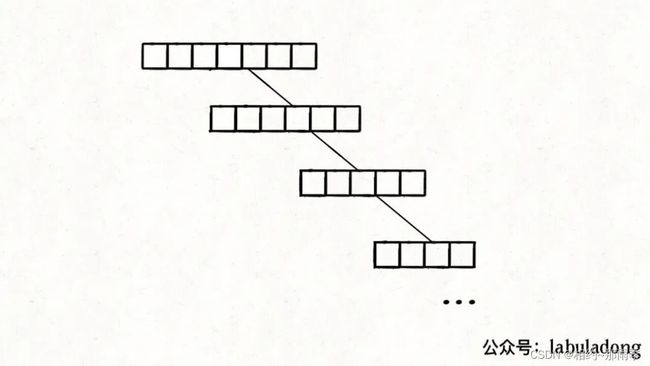
class Quick { public: void sort(vector<int>& nums) { shuffle(nums); // 洗牌算法,将输入的数组随机打乱,避免出现耗时的极端情况 sort(nums, 0, nums.size() - 1); // 排序整个数组(原地修改) } private: void sort(vector<int>& nums, int low, int high) { if (low >= high) return; // 注意:根据partition函数,p的范围:[low,high],故递归sort的判断应该是>=而非== // 对 nums[lo..hi] 进行切分,使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi] int p = partition(nums, low, high); sort(nums, low, p - 1); sort(nums, p + 1, high); } // 对 nums[lo..hi] 进行切分(关键函数!!!必背!) int partition(vector<int>& nums, int low, int high) { int pivot = nums[low]; int i = low + 1, j = high; // 尤其注意:把 i, j 定义为开区间,同时定义:[lo, i) <= pivot;(j, hi] > pivot // 当 i > j 时结束循环,以保证区间 [lo, hi] 都被覆盖 while (i <= j) { while (i < high && nums[i] <= pivot) { i++; } // 此 while 结束时恰好 nums[i] > pivot while (j > low && nums[j] > pivot) { j--; } // 此 while 结束时恰好 nums[j] <= pivot if (i >= j) break; // 如果走到这里,一定有:nums[i] > pivot && nums[j] < pivot // 所以需要交换 nums[i] 和 nums[j],保证 nums[low..i] < pivot < nums[j..high] swap(nums[i], nums[j]); } swap(nums[low], nums[j]); // 将 pivot 放到合适的位置,即 pivot 左边元素较小,右边元素较大 return j; } void shuffle(vector<int>& nums) { int n = nums.size(); for (int i = 0; i < n; i++) { int randIndex = rand() % (n - i) + i; // 生成 [i, n - 1] 的随机数 swap(nums[i], nums[randIndex]); } } };引入随机性:避免极端情况的发生(如下图:极端情况下二叉搜索树会退化成一个链表,导致操作效率大幅降低。),对整个数组执行
[洗牌算法]进行打乱。
-
时间复杂度:理想情况的时间复杂度是
O(NlogN)。空间复杂度:O(logN)。原因:partition执行的次数是二叉树节点的个数,每次执行的复杂度就是每个节点代表的子数组nums[lo..hi]的长度,所以总的时间复杂度就是整棵树中「数组元素」的个数(分析和“归并排序”一样)。由于快排没有使用任何辅助数组,所以空间复杂度就是递归堆栈的深度,也就是树高O(logN)。极端情况下(随机化后很难发生)的最坏时间复杂度是O(N^2),空间复杂度是O(N)。 -
注意:
快速排序是「不稳定排序」,与之相对的,前文讲的归并排序是「稳定排序」。
补充:洗牌算法
-
与排序相对的,是打乱。该算法又称:
「随机乱置算法」 -
分析洗牌算法正确性的【准则】:产生的结果必须有 n! 种可能,否则就是错误的。(因为一个长度为 n 的数组的全排列就有 n! 种,即:打乱结果总共有 n! 种)
-
核心思想:靠随机选取元素交换来获取随机性。
-
补充:详见
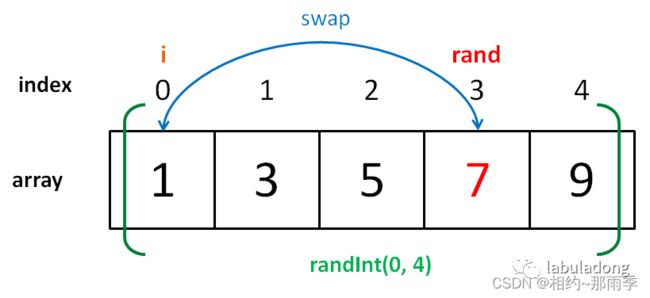
“数组——>随机算法”——> STL常用算法random_shuffle:洗牌指定范围内的元素随机调整次序(使用时记得加随机数种子,记得加对应头文件:srand((unsigned int)time(NULL)); // 对应 头文件:#include)// 第一种写法 void shuffle(vector<int>& arr) { int n = arr.size(); /******** 不同的写法,区别只有这两行 ********/ for (int i = 0; i < n; ++i) { int randIndex = rand() % (n - i) + i; // 从 i 到 最后n-1 随机选一个元素 /********************************************/ swap(arr[i], arr[randIndex]); } } // 第二种写法 for (int i = 0; i < n - 1; i++) int randIndex = rand() % (n - i) + i; // 第三种写法 for (int i = n - 1; i >= 0; i--) int randIndex = rand() % (i + 1); // 从 0 到 i 随机选一个元素 // 第四种写法 for (int i = n - 1; i > 0; i--) int randIndex = rand() % (i + 1); // 注意:如下写法❌——> 因为这种写法得到的所有可能结果有 n^n 种,而不是 n! 种,而且 n^n 一般不可能是 n! 的整数倍。 // 总结:概率均等是算法正确的衡量标准,所以下面这个算法是错误的。 // for (int i = 0; i <= n - 1; i++) // int randIndex = rand() % n; // 从 0 到 最后n-1 随机选一个元素根据前述准则验证该代码的准确性:假设传入这样一个
arr:vectorarr = { 1,3,5,7,9 }; -
第一种写法:
-
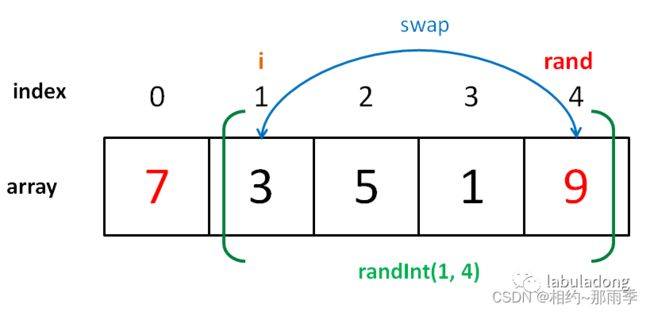
第二种写法: 少了
i = 4的这样一种情况,这种情况下只有一个可能取值,整个过程产生的所有可能结果仍然有5*4*3*2=5!=n!种,因为乘以 1 可有可无。 -
第三、四种写法: 只是将数组从后往前迭代而已,所有可能结果仍然有
1*2*3*4*5=5!=n!种
-
-
随机乱置算法的正确性衡量标准是:对于每种可能的结果出现的概率必须相等,也就是说要足够随机。——>
蒙特卡罗方法
4、归并排序(重要)
-
经典总结:先把左半边数组排好序,再把右半边数组排好序,然后把两半数组按序合并。——> 二叉树遍历时的后序位置处理。
-
归并排序的过程可以在逻辑上抽象成一棵二叉树,树上的每个节点的值可以认为是
nums[lo..hi],叶子节点的值就是数组中的单个元素: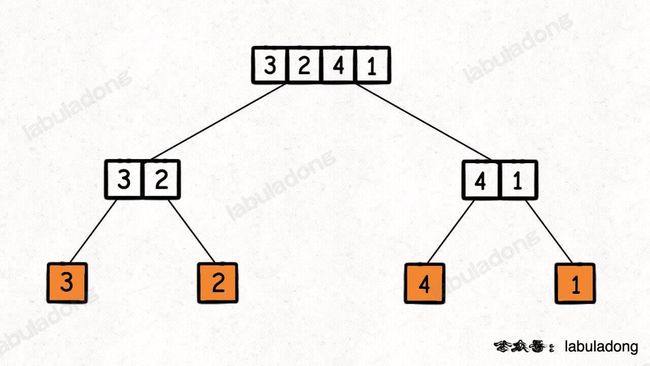
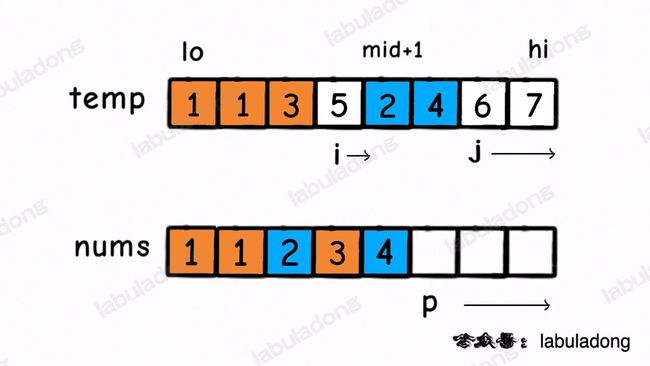
在每个节点的【后序位置】(左右子节点已被合并排序)执行
merge函数,合并排序两个子节点上的子数组为一个数组。把nums[lo..hi]理解成二叉树的节点,sort函数理解成二叉树的**遍历函数**,则整个过程如下: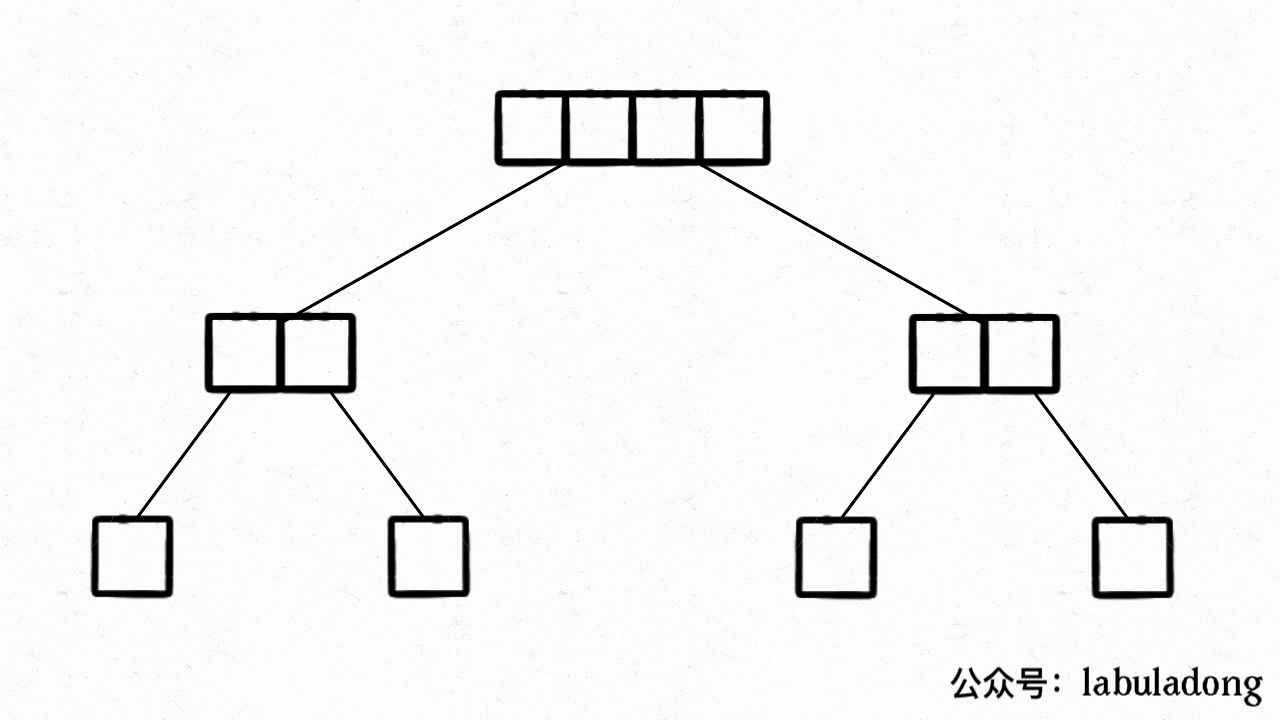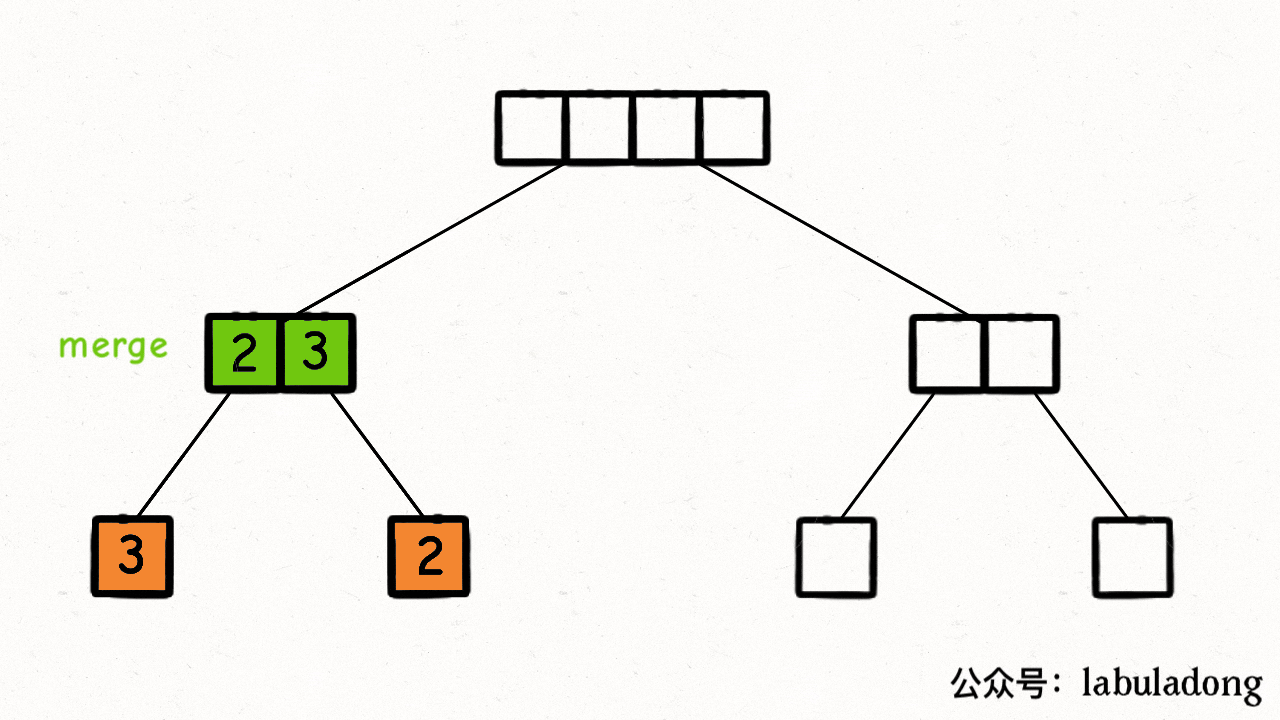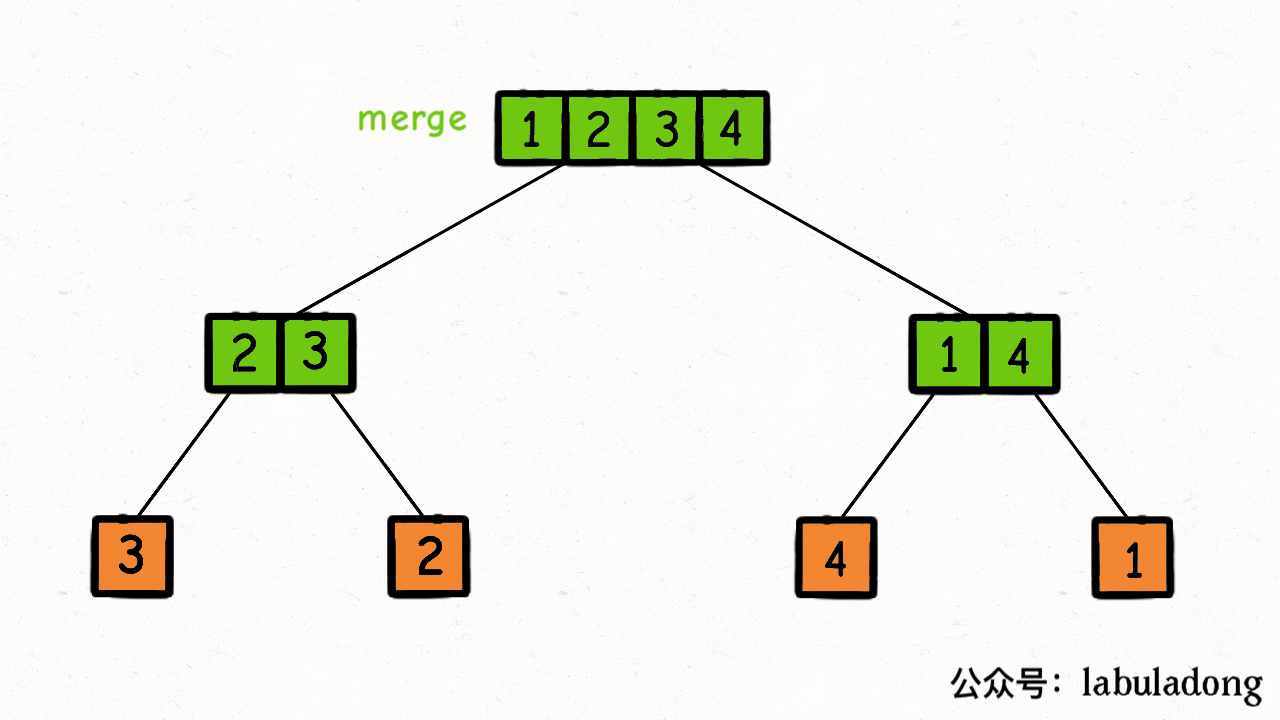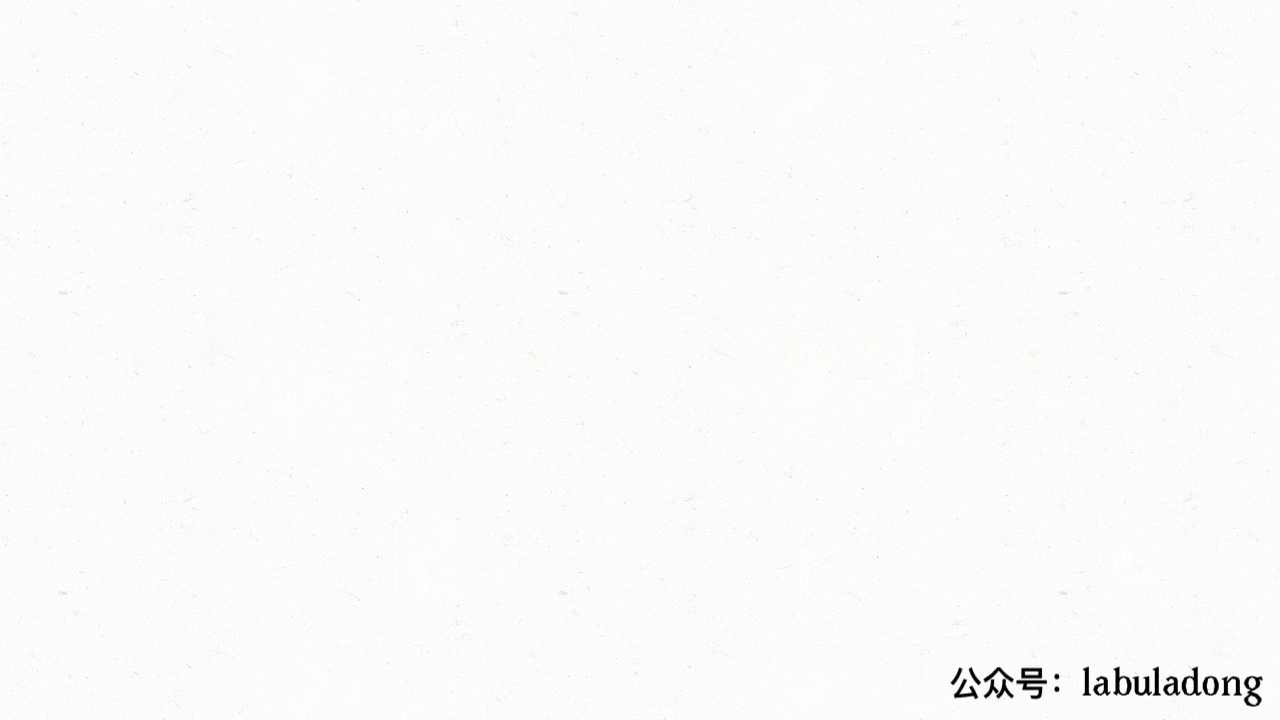
-
代码框架:
class Merge { public: // 留出调用接口 void sort(vector<int>& nums) { temp.resize(nums.size()); // 先给辅助数组开辟内存空间 sort(nums, 0, nums.size() - 1); // 排序整个数组(原地修改) } private: vector<int> temp; // 用于辅助合并有序数组 // 定义:将子数组 nums[lo..hi] 进行排序 void sort(vector<int>& nums, int low, int high) { if (low == high) return; // 单个元素不用排序 int mid = low + (high - low) / 2; // 这样写是为了防止溢出,效果等同于 (hi + lo) / 2 sort(nums, low, mid); // 先对【左半部分】数组 nums[lo..mid] 排序 sort(nums, mid + 1, high); // 再对【右半部分】数组 nums[mid+1..hi] 排序 merge(nums, low, mid, high); // 将两部分有序数组【合并】成一个【有序】数组 } // 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组【合并】成一个【有序】数组(关键函数!!!必背!) void merge(vector<int>& nums, int low, int mid, int high) { for (int i = low; i <= high; i++) { temp[i] = nums[i]; // 先把 nums[lo..hi] 复制到辅助数组中,以便合并后结果能直接存入 nums } // 数组双指针技巧,合并两个有序数组 int i = low, j = mid + 1; for (int p = low; p <= high; p++) { // 注意:次序不能搞错!先判断左or右半边数组是否已经被合并,然后再判断元素大小 if (i == mid + 1) { nums[p] = temp[j++]; // 左半边数组已全部被合并 } else if (j == high + 1) { nums[p] = temp[i++]; // 右半边数组已全部被合并 } else if (temp[i] > temp[j]) { nums[p] = temp[j++]; } else { // temp[i] <= temp[j] nums[p] = temp[i++]; } } } }; -
时间复杂度:O(NlogN)。原因:执行的次数是二叉树节点的个数,每次执行的复杂度就是每个节点代表的子数组的长度,所以总的时间复杂度就是整棵树中「数组元素」的个数。所以从整体上看,这个二叉树高度是logN + 1(因为一个叶子节点代表一个数组元素,数组元素个数 = 叶子节点个数),其中每一层的元素个数=原数组的长度N,所以总的时间复杂度就是O(NlogN + N) = O(NlogN)。eg:设
N = 4,故logN + 1 = 3,这棵树「数组元素」的个数= 4 + (2 + 2) + (1 + 1 + 1 + 1) == N*(logN + 1) = 12 -
空间复杂度:程序开始时创建的临时辅助数组temp+ 调用的递归栈空间= N + logN,所以最终的空间复杂度为O(N)。
三、时间复杂度 O(n) 级排序算法
1、计数排序(重要)
-
注意:在对一定范围内的整数排序时,它的复杂度为
Ο(n+k)(其中 k 是整数的范围大小)。故计数排序基于一个假设:待排序数列的所有数均为整数,且出现在(0,k)的区间之内。如果 k(待排数组的最大值) 过大则会引起较大的空间复杂度,一般是用来排序 0 到 100 之间的数字的最好的算法,但不适合按字母顺序排序人名。计数排序不是比较排序,排序的速度快于任何比较排序算法。 -
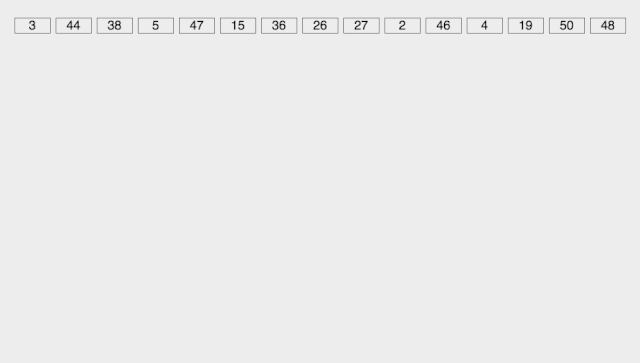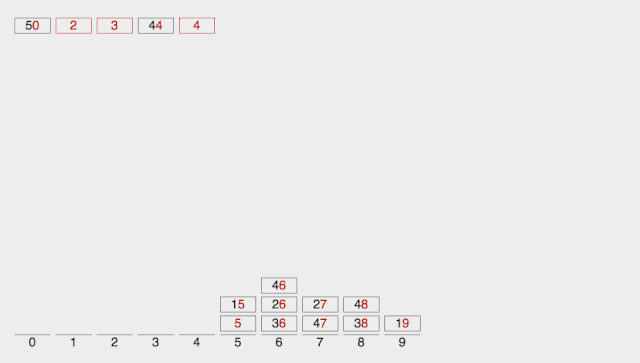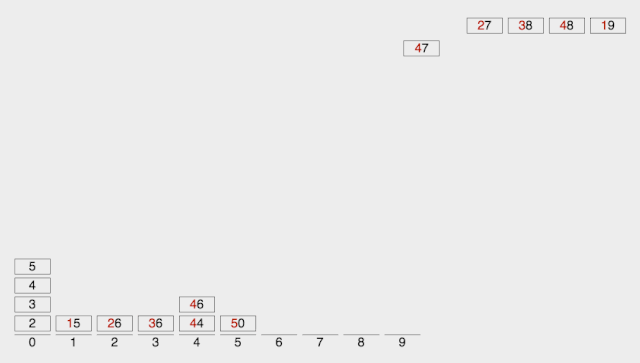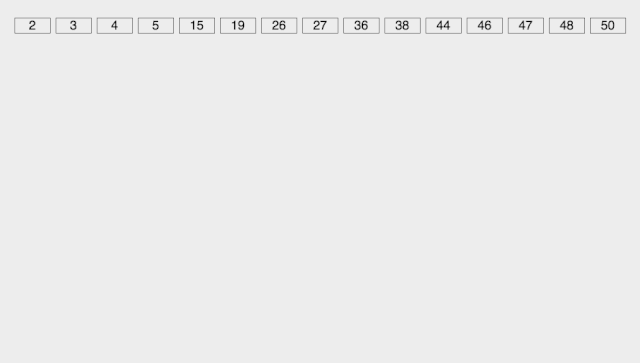
举个如下:班上有 10名同学:他们的考试成绩分别是:7, 8, 9, 7, 6, 7, 6, 8, 6, 6,他们需要按照成绩从低到高坐到 0~9共 10个位置上。用计数排序完成这一过程需要以下几步:
1. 第一步仍然是计数,统计出:4名同学考了 6分,3名同学考了 7分,2名同学考了 8分,1名同学考了 9分;
2. 然后从头遍历数组:
第一名同学考了 7分,共有 4个人比他分数低,所以第一名同学坐在 4号位置(也就是第 5个位置);
第二名同学考了 8分,共有 7个人(4 + 3)比他分数低,所以第二名同学坐在 7号位置;
第三名同学考了 9分,共有 9个人(4 + 3 + 2)比他分数低,所以第三名同学坐在 9号位置;
第四名同学考了 7分,共有 4个人比他分数低,并且之前已经有一名考了 7分的同学坐在了 4号位置,所以第四名同学坐在 5号位置。
3. …依次完成整个排序 -
基本过程:
1. 找出待排序的数组中最大和最小的元素;
2. 统计数组中每个值为i的元素出现的次数,存入数组vecCount的第i项;
3. 对所有的计数累加(从vecCount中的第一个元素开始,每一项和前一项相加);
4. 向填充目标数组:将每个元素i放在新数组的第vecCount[i]项,每放一个元素就将vecCount[i]减去1; -
代码如下:
vector<int> vecRaw = { 0,5,7,9,6,3,4,5,2, }; vector<int> vecObj(vecRaw.size(), 0); // 计数排序 void CountSort(vector<int>& vecRaw, vector<int>& vecObj) { if (vecRaw.size() == 0) // 确保待排序容器非空 return; int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1; // 使用 vecRaw 的最大值 + 1 作为计数容器 countVec 的大小 vector<int> vecCount(vecCountLength, 0); for (int i = 0; i < vecRaw.size(); i++) // 统计每个键值出现的次数 vecCount[vecRaw[i]]++; for (int i = 1; i < vecCountLength; i++) // 后面的键值出现的位置为前面所有键值出现的次数之和 vecCount[i] += vecCount[i - 1]; for (int i = vecRaw.size(); i > 0; i--) // 将键值放到目标位置,此处逆序是为了保持相同键值的稳定性 vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1]; } -
计数排序与
O(nlogn)级排序算法的本质区别
答:可以从决策树的角度和概率的角度来理解。
1. 决策树角度:以包含三个整数的数组[a,b,c]为例,基于比较的排序算法的排序过程可以抽象为这样一棵决策树:
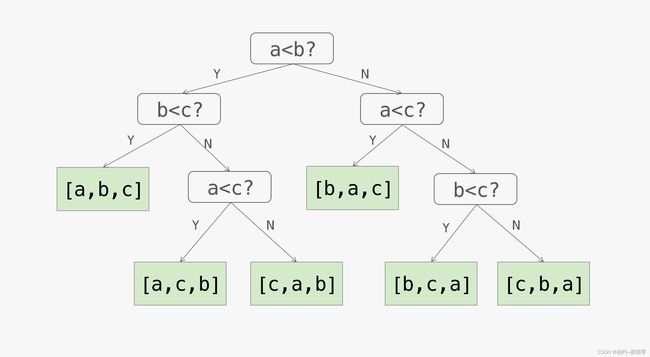
- 这棵决策树上的每一个叶结点都对应了一种可能的排列,从根结点到任意一个叶结点之间的最短路径(也称为**「简单路径」)的长度,表示的是完成对应排列的比较次数。所以从根结点到叶结点之间的最长简单路径的长度,就表示比较排序算法中最坏情况下**的比较次数。
- 设决策树的高度为
h,叶结点的数量为l,排序元素总数为n。因为叶结点最多有n!个,所以我们可以得到:n! ≤ l,又因为一棵高度为h的二叉树,叶结点的数量最多为2^h,所以我们可以得到:n! ≤ l ≤ 2^h;对该式两边取对数,可得:h≥log(n!);由斯特林(Stirling)近似公式,可知lg(n!) = O(nlogn);所以h ≥ log(n!) = O(nlogn)。 - 于是我们可以得出以下定理:《算法导论》定理 8.1:在最坏情况下,任何比较排序算法都需要做
O(nlogn)次比较。 - 到这里我们就可以得出结论:如果基于比较来进行排序,无论怎么优化都无法突破
O(nlogn)的下界。计数排序和基于比较的排序算法相比,根本区别就在于:它不是基于比较的排序算法,而是利用了数字本身的属性来进行的排序。整个计数排序算法中没有出现任何一次比较。
2. 概率角度:
相信大家都玩过「猜数字」游戏:一方从[1,100]中随机选取一个数字,另一方来猜。每次猜测都会得到「高了」或者「低了」的回答。怎样才能以最少的次数猜中呢?
答案很简单:二分。
二分算法能够保证每次都排除一半的数字。每次猜测不会出现惊喜(一次排除了多于一半的数字),也不会出现悲伤(一次只排除了少于一半的数字),因为答案的每一个分支都是等概率的,所以它在最差的情况下表现是最好的,猜测的一方在logn次以内必然能够猜中。
基于比较的排序算法与「猜数字」是类似的,每次比较,我们只能得到a > b或者a ≤ b两种结果,如果我们把数组的全排列比作一块区域,那么每次比较都只能将这块区域分成两份,也就是说每次比较最多排除掉1/2的可能性。再来看计数排序算法,计数排序时申请了长度为k的计数数组,在遍历每一个数字时,这个数字落在计数数组中的可能性共有k种,但通过数字本身的大小属性,我们可以「一次」把它放到正确的位置上。相当于一次排除了(k−1)/k种可能性。
这就是计数排序算法比基于比较的排序算法更快的根本原因。
2、基数排序
-
举例:比如我们对
999, 997, 866, 666这四个数字进行基数排序,过程如下:
先看第一位基数:6比8小,8比9小,所以666是最小的数字,866是第二小的数字,暂时无法确定两个以9开头的数字的大小关系。
再比较9开头的两个数字,看他们第二位基数:9和9相等,暂时无法确定他们的大小关系。
再比较99开头的两个数字,看他们的第三位基数:7比9小,所以997小于999。 -
基数排序可以分为以下三个步骤:
找出数组中最大的数字的位数maxDigitLength。
获取数组中每个数字的基数。
遍历maxDigitLength轮数组,每轮按照基数对其进行排序。 -
代码如下:
vector<int> vecRaw = { 0,-5,7,29,6,37,4,5,2, }; vector<int> vecObj(vecRaw.size(), 0); void RadixSort(vector<int>& vecRaw, vector<int>& vecObj) { if (vecRaw.size() == 0) return; // 确保待排序容器非空 // 找出最长的数 int maxVal = max(abs(*max_element(vecRaw.begin(), vecRaw.end())), abs(*min_element(vecRaw.begin(), vecRaw.end()))); // 计算最长数字的长度 int maxDigitLength = 0; while (maxVal != 0) { maxDigitLength++; maxVal /= 10; } // 使用计数排序算法对基数进行排序,下标 [0, 18] 对应基数 [-9, 9] vector<int> counting(19); int dev = 1; // 使用倒序遍历的方式完成计数排序 for (int i = 0; i < maxDigitLength; i++) { for (int value : vecRaw) { int radix = value / dev % 10 + 9; // 下标调整 counting[radix]++; } for (int j = 1; j < counting.size(); j++) { counting[j] += counting[j - 1]; } for (int j = vecRaw.size() - 1; j >= 0; j--) { int radix = vecRaw[j] / dev % 10 + 9; // 下标调整 vecObj[--counting[radix]] = vecRaw[j]; } vecRaw = vecObj; // 计数排序完成后,将结果数组 vecObj 拷贝回原数组 vecRaw fill(counting.begin(), counting.end(), 0); // 将计数数组重置为 0 dev *= 10; } }
3、桶排序
-
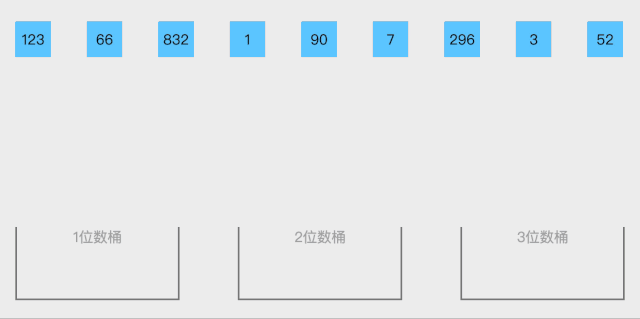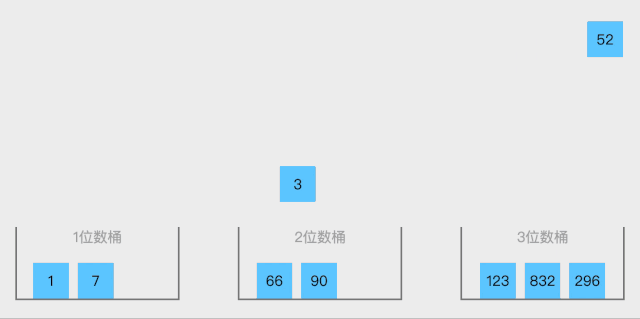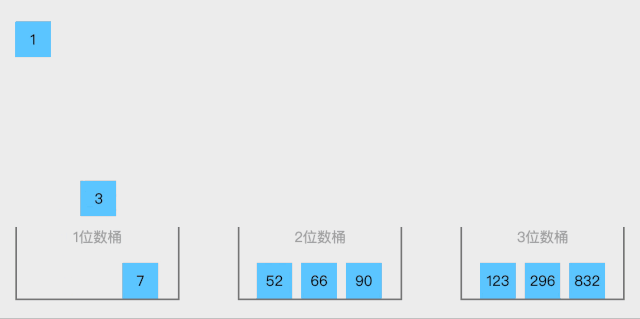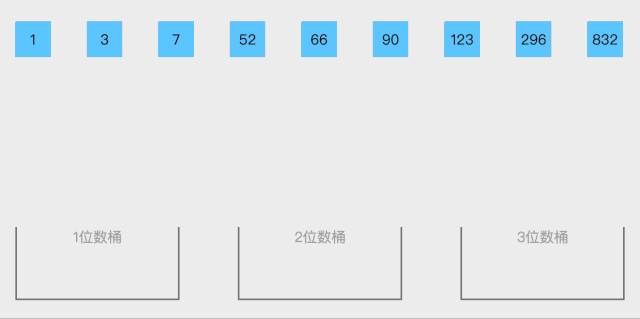
桶排序的思想是:
1. 将区间划分为n个相同大小的子区间,每个子区间称为一个桶
2. 遍历数组,将每个数字装入桶中
3. 对每个桶内的数字单独排序,这里需要采用其他排序算法,如插入、归并、快排等
4. 最后按照顺序将所有桶内的数字合并起来 -
代码如下:
const int BUCKET_NUM = 10; struct ListNode { explicit ListNode(int i = 0) :mData(i), mNext(NULL) {} ListNode* mNext; int mData; }; ListNode* insert(ListNode* head, int val) { ListNode dummyNode; ListNode* newNode = new ListNode(val); ListNode* pre, * curr; dummyNode.mNext = head; pre = &dummyNode; curr = head; while (NULL != curr && curr->mData <= val) { pre = curr; curr = curr->mNext; } newNode->mNext = curr; pre->mNext = newNode; return dummyNode.mNext; } ListNode* Merge(ListNode* head1, ListNode* head2) { ListNode dummyNode; ListNode* dummy = &dummyNode; while (NULL != head1 && NULL != head2) { if (head1->mData <= head2->mData) { dummy->mNext = head1; head1 = head1->mNext; } else { dummy->mNext = head2; head2 = head2->mNext; } dummy = dummy->mNext; } if (NULL != head1) dummy->mNext = head1; if (NULL != head2) dummy->mNext = head2; return dummyNode.mNext; } void BucketSort(int n, vector<int>& arr) { vector<ListNode*> buckets(BUCKET_NUM, (ListNode*)(0)); for (int i = 0; i < n; ++i) { int index = arr[i] / BUCKET_NUM; ListNode* head = buckets.at(index); buckets.at(index) = insert(head, arr[i]); } ListNode* head = buckets.at(0); for (int i = 1; i < BUCKET_NUM; ++i) { head = Merge(head, buckets.at(i)); } for (int i = 0; i < n; ++i) { arr[i] = head->mData; head = head->mNext; } }