MATLAB实现偏最小二乘回归（PLSR）数学建模算法

偏最小二乘回归（Partial Least Squares Regression，简称PLS回归）是一种多元回归分析方法，用于处理具有多重共线性和高维数据的情况。它结合了主成分分析和多元线性回归的特点，旨在降低预测模型中的自变量之间的共线性，并通过捕捉自变量和因变量之间的主要关系来建立模型。

PLS回归的核心思想是通过找到一组新的变量（称为部分最小二乘变量或PLS成分），这些新变量是原始自变量的线性组合，同时与因变量具有最大的协方差。这样可以在较低维度上保留数据的主要信息，同时降低了多重共线性的影响。

PLS回归在处理高维数据、小样本问题以及解决多重共线性困扰的情况下表现出色。它被广泛应用于化学、生物学、金融等领域，特别是在需要同时考虑多个自变量对因变量影响的情境中。

---

MATLAB的代码实现如下：

clc,clear, ab0=load('data11_1.txt');
mu=mean(ab0), sig=std(ab0) %求均值和标准差
rr=corrcoef(ab0)  %求相关系数矩阵
ab=zscore(ab0); %数据标准化
a=ab(:,[1:3]);b=ab(:,[4:end]);  %提出标准化后的自变量和因变量数据
[XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] =plsregress(a,b)
contr=cumsum(PCTVAR,2) %求累积贡献率
xw=a\XS  %求自变量提出成分系数，每列对应一个成分，这里xw等于stats.W
yw=b\YS  %求因变量提出成分的系数
ncomp=input('请根据PCTVAR的值确定提出成分对的个数ncomp=');
[XL2,YL2,XS2,YS2,BETA2,PCTVAR2,MSE2,stats2] =plsregress(a,b,ncomp)
n=size(a,2); m=size(b,2);%n是自变量的个数,m是因变量的个数
beta3(1,:)=mu(n+1:end)-mu(1:n)./sig(1:n)*BETA2([2:end],:).*sig(n+1:end); %原始数据回归方程的常数项
beta3([2:n+1],:)=(1./sig(1:n))'*sig(n+1:end).*BETA2([2:end],:) %计算原始变量x1,...,xn的系数，每一列是一个回归方程
bar(BETA2','k')   %画直方图
yhat=repmat(beta3(1,:),[size(a,1),1])+ab0(:,[1:n])*beta3([2:end],:)  %求y1,..,ym的预测值
ymax=max([yhat;ab0(:,[n+1:end])]); %求预测值和观测值的最大值
%下面画y1,y2,y3的预测图，并画直线y=x
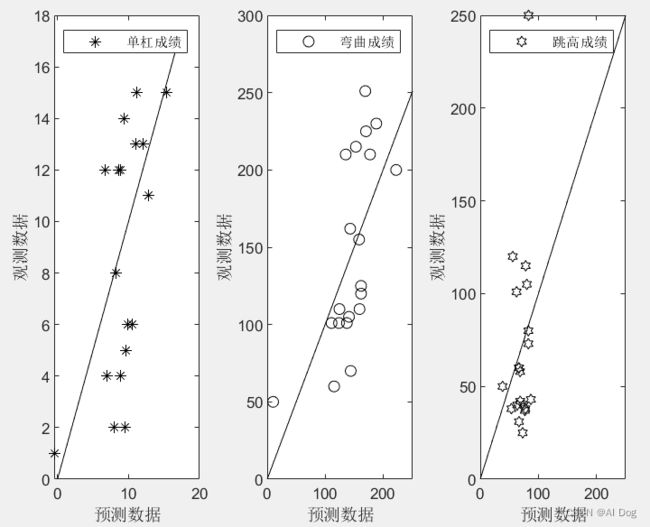
figure, subplot(1,3,1)
plot(yhat(:,1),ab0(:,n+1),'*',[0:ymax(1)],[0:ymax(1)],'Color','k')
legend('单杠成绩','Location','northwest')
xlabel('预测数据'), ylabel('观测数据'), subplot(1,3,2)
plot(yhat(:,2),ab0(:,n+2),'O',[0:ymax(2)],[0:ymax(2)],'Color','k')
legend('弯曲成绩','Location','northwest')
xlabel('预测数据'), ylabel('观测数据'), subplot(1,3,3)
plot(yhat(:,3),ab0(:,end),'H',[0:ymax(3)],[0:ymax(3)],'Color','k')
legend('跳高成绩','Location','northwest')
xlabel('预测数据'), ylabel('观测数据')

运行结果如下：