Path Sum (路径和)----(LeetCode112+LeetCode113+LeetCode437)

(一) Leetcode 112 Path Sum

1.题意

给定一个二叉树，找一条从根节点到叶子结点的路径，使得这条路径的和等于给定的sum。最终返回的是否存在一条路径？

2.示例

sum = 22
输出：true

3.解题思路及代码实现

如示例所示的树，询问是否有一条从根节点到叶子节点的路径，使得路径上的和等于输入值，当sum==22时，存在一条路径 5 -> 4 -> 11 -> 2 使得 5+4+11+2 == 22。
因此既可以用深度优先搜索来解题，也可以用先序遍历来做，两者效果相当。

DFS实现的java代码如下所示：
其实也是递归操作：
关键在函数定义！定义！根据定义写推导式和终止条件，写完就直接结束，千万别一个一个拿数据再去代。

public class Path_Sum_112 {
    public boolean hasPathSum(TreeNode root, int sum) {
        if(root==null) return false;
        if(root.left==null && root.right==null) return root.val==sum;
        return dfs(root,root.val,sum)>0;  //rec初始化为根节点的值
    }
    
    public int dfs(TreeNode root,int rec,int sum){ //通过flag的值来判断只要有一条路径成立就可以了
        if(root.left==null && root.right==null)  //到达叶子节点，判断这条路径之和是否等于输入值sum
            return rec-sum==0?1:0;  //三目运算符，当rec-sum=0时返回1，不等于0时返回0
        int flag=0;
        if(root.left!=null)   //向左子树搜
            flag += dfs(root.left,rec+root.left.val,sum);
        if(root.right!=null)
            flag += dfs(root.right,rec+root.right.val,sum);
        return flag; 
    }
}

class Solution(object):
    def hasPathSum(self, root, sum):
        if not root: return False
       
        def dfs(root, target): # 在以root为根结点的树中，能否找到一条从根结点到叶子结点的路径，使得路径和等于target
            # 第三步，要是到达叶子节点后的空节点还是没有返回值，则返回False
            if not root:  return False 
            
            # 第一步，递归出来的条件，到达了叶子节点并且叶子节点值刚好等于target，说明这条路径到了！
            if not root.left and not root.right and root.val == target: 
                return True
            # 第二步，子问题分解为
            # 以root.left为根节点时是否有路径之和为target-root.val 或者 
            # 以root.right为根节点时是否有路径之和为target-root.val
            return dfs(root.left, target-root.val) or dfs(root.right, target-root.val)
        
        return dfs(root, sum)

(二) Leetcode 113 Path Sum II

1.题意

给定一个二叉树，找一条从根节点到叶子结点的路径，使得这条路径的和等于给定的sum。最终返回的是多条存在的路径，用数组存储路径。

2.示例

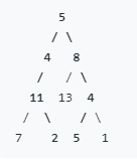
输入：sum = 22
输出：
[
[5,4,11,2],
[5,8,4,5]
]

3.解题思路及代码实现

这道题与上一道LeetCode112很类似，都是使用深度优先遍历或先序遍历来做，不过这道题需要在遍历时保存路径，当路径满足求和等于Sum时把这条路径加入到二维数组之中，最后整棵树都遍历结束之后再返回二维数组。
此外，记录路径需要用到栈。

DFS实现的java代码如下所示：

public class Path_Sum_II_113 {
    private List<List<Integer>> ans = new ArrayList<List<Integer>>();
    
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        if(root==null) return ans;
        Stack<Integer> path = new Stack<>(); //用来保存一条路径
        dfs(root,sum,path);
        return ans;
    }
    
    public void dfs(TreeNode root,int sum,Stack<Integer> path){
        path.push(root.val);
        if(root.left==null && root.right==null) //到达叶子节点
             if(root.val==sum)   ans.add(new ArrayList<>(path));
        if(root.left!=null) //向左子树搜
            dfs(root.left,sum-root.val,path);
        if(root.right!=null)
            dfs(root.right,sum-root.val,path);
        path.pop();//感觉这就是回溯
    }
}

python实现：

class Solution(object):
    def pathSum(self, root, sum):
        self.res = []
        if not root: return []
        
        def dfs(root, Sum, path):
            if not root: return
            path.append(root.val)
            if not root.left and not root.right and root.val==Sum: # 找到一条路径
                self.res.append(path[:])
            dfs(root.left, Sum-root.val, path)
            dfs(root.right, Sum-root.val, path)
            path.pop()
        
        dfs(root, sum, [])
        return self.res

(三) Leetcode 437 Path Sum III

1.题意

给定一个二叉树，找一条从节点1到叶子2的路径(自顶向下，无需是从根节点到叶子节点)，使得这条路径的和等于给定的sum。最终返回的是路径的个数。

2.示例

3.解题思路及代码实现（python）

递归来做，对于当前节点node，计算以自己为开始的路径数（这条路径和等于sum），再分别计算以自己的左儿子，右儿子为开始的路径数！
对于每一个节点都是这么计算，递归下去就行了！！！

• 自顶向下，时间复杂度为O(N^2)，还能优化

class Solution(object):
    def pathSum(self, root, sum):
        def count(node, sum): # 自己为开头的路径数，不需要到达叶子节点
            if not node: return 0
            isMe = 1 if node.val == sum else 0
            leftBrother = count(node.left, sum - node.val)
            rightBrother = count(node.right, sum - node.val)
            return isMe + leftBrother + rightBrother
    	
    	# 递归版的先序遍历
        if not root: return 0
        pathInLeading = count(root, sum) # 自己为开头的路径数
        leftPathSum = self.pathSum(root.left, sum) # 左边路径总数（中间节点路径）
        rightPathSum = self.pathSum(root.right, sum) # 右边路径总数
        return leftPathSum + rightPathSum + pathInLeading # 以自己，再以左儿子，右儿子为开始的路径总数

• 时间复杂度为O(N)的方法：以空间换时间，缓存中间结果
  
  参考：https://leetcode.com/problems/path-sum-iii/discuss/141424/Python-step-by-step-walk-through.-Easy-to-understand.-Two-solutions-comparison.-%3A-)

class Solution(object):
    def pathSum(self, root, sum):
    	def preOrder(root, sum, curPathSum, cache):
            if not root: return
            # 访问根节点
            curPathSum += root.val  # 从root到当前结点的路径和
            oldPathSum = curPathSum - sum  # 剩余还需要的路径和
            
            self.res += cache[oldPathSum]  # 看看缓存中有没有还需要的路径和
            cache[curPathSum] += 1
            
            preOrder(root.left, sum, curPathSum, cache)
            preOrder(root.right, sum, curPathSum, cache)
            # 回溯时到其他路径后需要减一
            cache[curPathSum] -= 1
           
        self.res = 0
        cache = collections.defaultdict(int)
        cache[0] = 1  # 初始化时root==sum时也是一条路径
        preOrder(root, sum, 0, cache)
        return self.res