【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【DFS/树形DP】2023C-悄悄话花费的时间【欧弟算法】全网注释最详细分类最全的华为OD真题题解

题目描述与示例

题目描述

给定一个二叉树，每个节点上站着一个人，节点数字表示父节点到该节点传递悄悄话需要花费的时间。

初始时，根节点所在位置的人有一个悄悄话想要传递给其他人，求二叉树所有节点上的人都接收到悄悄话花费的时间。

输入描述

给定一个数组表示二叉树，-1 表示空节点

输出描述

返回所有节点都接收到悄悄话花费的时间

示例

输入

0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2

输出

38

说明

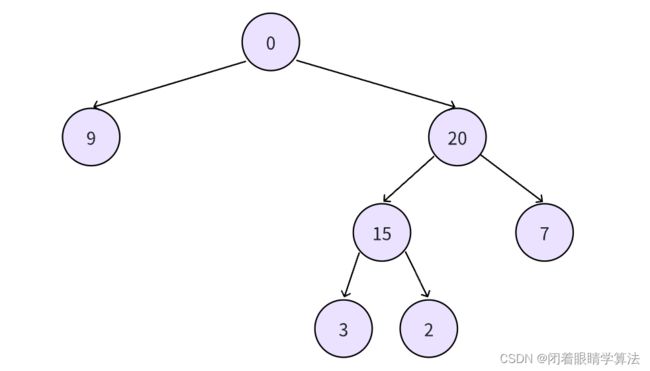
表示如下二叉树

解题思路

分两步完成题目。首先根据所给定的数组还原二叉树，再进行DFS找到从根节点到叶节点和最大的路径。

建树有两种写法，寻找最大路径也有两种写法。故本题至少有四种解法，大家可以自行选择。

构建二叉树

首先需要明确题目所给定的数组是如何表示一棵二叉树的。以示例

0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2

为例，把其中的空节点在树状结构中补全可以得到。

容易发现，输入数组类似于二叉树的层序遍历结果，但把空节点也一并输出。

如果标注出节点在原数组中的下标，可以看到。

容易观察出规律：如果某一个节点在数组下标为i，那么其左孩子和右孩子（如果存在，不为-1）在数组中的下标分别为i*2+1和i*2+2。

基于这个规律，可以很容易地使用递归或者迭代的方式还原出二叉树。其中递归方法效率更高也更简洁，但是迭代方法对于初学者更加友好，大家可以自由选择。

迭代写法

# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

nums = list(map(int, input().split()))
n = len(nums)

# 初始化一个长度为n的列表node_lst，idx位置储存值为nums[idx]的节点
# 初始化均为空节点
node_lst = [None] * n
# 构建节点
for idx in range(n):
    # 如果值不为-1，则构建一个节点
    if nums[idx] != -1:
        node_lst[idx] = Node(nums[idx])

# 构建节点之间的连接关系
for idx in range(n):
    # 如果nums[idx]值不为-1，找到node_lst[idx]的左右节点并连接
    if nums[idx] != -1:
        if idx*2+1 < n:
            node_lst[idx].left = node_lst[idx*2+1]
        if idx*2+2 < n:
            node_lst[idx].right = node_lst[idx*2+2]

# node_lst中的第一个节点即为根节点
root = node_lst[0]

递归写法

# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

# 构建树结构的递归函数
def build_tree(idx, nums):
    # 如果idx超过了数组长度，或者在nums中为-1
    # 表示当前是一个空节点，返回None
    if idx >= len(nums) or nums[idx] == -1:
        return None
    # 否则，当前节点node的值为nums[idx]
    # 对idx*2+1和idx*2+2这两个位置进行递归调用
    # 分别为node的左节点和右节点
    # 同时需要将node传回上一层递归
    else:
        node = Node(nums[idx])
        node.left = build_tree(idx*2+1, nums)
        node.right = build_tree(idx*2+2, nums)
        return node

nums = list(map(int, input().split()))
# 构建二叉树，返回根节点
root = build_tree(0, nums)

寻找最大路径

还原出二叉树之后，剩下的工作就是寻找从根节点到叶节点的最大和路径。显然应该使用DFS来实现。存在自底向上和自顶向下两种不同写法。

自顶向下DFS

自顶向下方法类似于回溯，从上往下记录路径和。考虑递归三要素。

1. 递归终止条件
   1. 遇到叶节点，更新全局答案变量。
2. 递归子问题
   1. 把当前节点node的值node.val计入路径和中
   2. 如果左节点或右节点不为空，递归地考虑左节点和右节点
3. 递归入口
   1. 从根节点root开始递归
   2. 初始时路径和path_sum为0

# 自顶向下的DFS：从上往下记录路径和
def dfs(path_sum, node):
    global ans
    # 遇到一个叶节点，更新答案
    if node.left == None and node.right == None:
        ans = max(path_sum + node.val, ans)
        return
    # 如果左节点非空，对左节点进行递归调用
    if node.left:
        dfs(path_sum + node.val, node.left)
    # 如果右节点非空，对右节点进行递归调用
    if node.right:
        dfs(path_sum + node.val, node.right)
    return

# 初始化答案变量
ans = 0
# 递归调用入口，路径和为0，初始节点为root
dfs(0, root)
print(ans)

自底向上DFS

自底向上方法的核心在于优先计算以子节点为根节点的最大路径和，并把结果回传，从下往上计算路径和。考虑递归三要素。

1. 递归终止条件
   1. 遇到空节点，返回0。表示此时空节点对路径和没有贡献。
2. 递归子问题
   1. 递归函数dfs(node)的返回值表示，当以node作为根节点时，node到其下方的叶节点的最大路径和。
   2. 考虑node的左节点和右节点递归调用的结果dfs(node.left)和dfs(node.right)，其中的较大值应该被考虑进以node作为根节点的最大路径和。
   3. 把当前节点node的值node.val计入当前路径和path_sum中
   4. 将当前最大路径和path_sum传回上一层递归
3. 递归入口
   1. 从根节点root开始递归

# 自底向上的DFS：从下往上更新路径和
def dfs(node):
    # 遇到空节点，返回0。表示此时空节点对路径和没有贡献。
    if node == None:
        return 0
    else:
        # 计算左节点和右节点递归调用的结果
        # 表示以node.left和node.right为根节点的最大路径和
        left_path_sum = dfs(node.left)
        right_path_sum = dfs(node.right)
        # 在两者中选择较大值，作为以当前节点node为根节点的最大路径和
        path_sum = max(left_path_sum, right_path_sum) + node.val
        return path_sum


# 递归调用入口，传入root
ans = dfs(root)
print(ans)

这也是一种树形dp思想的体现。

代码

解法一：迭代写法建树+自顶向下DFS

python

# 题目：【DFS】2023C-悄悄话花费的时间
# 分值：200
# 作者：闭着眼睛学数理化
# 算法：DFS/树（解法一：迭代写法建树+自顶向下DFS）
# 代码看不懂的地方，请直接在群上提问


# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

nums = list(map(int, input().split()))
n = len(nums)

# 初始化一个长度为n的列表node_lst，idx位置储存值为nums[idx]的节点
# 初始化均为空节点
node_lst = [None] * n
# 构建节点
for idx in range(n):
    # 如果值不为-1，则构建一个节点
    if nums[idx] != -1:
        node_lst[idx] = Node(nums[idx])

# 构建节点之间的连接关系
for idx in range(n):
    # 如果nums[idx]值不为-1，找到node_lst[idx]的左右节点并连接
    if nums[idx] != -1:
        if idx*2+1 < n:
            node_lst[idx].left = node_lst[idx*2+1]
        if idx*2+2 < n:
            node_lst[idx].right = node_lst[idx*2+2]


# 自顶向下的DFS：从上往下记录路径和
def dfs(path_sum, node):
    global ans
    # 遇到一个叶节点，更新答案
    if node.left == None and node.right == None:
        ans = max(path_sum + node.val, ans)
        return
    # 如果左节点非空，对左节点进行递归调用
    if node.left:
        dfs(path_sum + node.val, node.left)
    # 如果右节点非空，对右节点进行递归调用
    if node.right:
        dfs(path_sum + node.val, node.right)
    return

# node_lst中的第一个节点即为根节点
root = node_lst[0]
# 初始化答案变量
ans = 0
# 递归调用入口，路径和为0，初始节点为root
dfs(0, root)
print(ans)

java

import java.util.Scanner;

class Node {
    int val;
    Node left, right;

    public Node(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

public class Main {
    static int ans = 0;

    public static void dfs(int pathSum, Node node) {
        if (node.left == null && node.right == null) {
            ans = Math.max(pathSum + node.val, ans);
            return;
        }
        if (node.left != null) {
            dfs(pathSum + node.val, node.left);
        }
        if (node.right != null) {
            dfs(pathSum + node.val, node.right);
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int[] nums = new int[1000];
        int n = 0;
        while (scanner.hasNextInt()) {
            nums[n++] = scanner.nextInt();
        }

        Node[] nodeList = new Node[n];
        for (int i = 0; i < n; i++) {
            if (nums[i] != -1) {
                nodeList[i] = new Node(nums[i]);
            }
        }

        for (int i = 0; i < n; i++) {
            if (nums[i] != -1) {
                if (i * 2 + 1 < n) {
                    nodeList[i].left = nodeList[i * 2 + 1];
                }
                if (i * 2 + 2 < n) {
                    nodeList[i].right = nodeList[i * 2 + 2];
                }
            }
        }

        Node root = nodeList[0];
        ans = 0;
        dfs(0, root);
        System.out.println(ans);
    }
}

cpp

#include 
#include 
using namespace std;

class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node(int val) {
        this->val = val;
        left = nullptr;
        right = nullptr;
    }
};

void dfs(int path_sum, Node* node, int& ans) {
    if (!node->left && !node->right) {
        ans = max(path_sum + node->val, ans);
        return;
    }
    if (node->left) {
        dfs(path_sum + node->val, node->left, ans);
    }
    if (node->right) {
        dfs(path_sum + node->val, node->right, ans);
    }
}

int main() {
    vector<int> nums;
    int num;
    while (cin >> num) {
        nums.push_back(num);
    }
    int n = nums.size();

    vector<Node*> nodeList(n, nullptr);
    for (int i = 0; i < n; ++i) {
        if (nums[i] != -1) {
            nodeList[i] = new Node(nums[i]);
        }
    }

    for (int i = 0; i < n; ++i) {
        if (nums[i] != -1) {
            if (i * 2 + 1 < n) {
                nodeList[i]->left = nodeList[i * 2 + 1];
            }
            if (i * 2 + 2 < n) {
                nodeList[i]->right = nodeList[i * 2 + 2];
            }
        }
    }

    Node* root = nodeList[0];
    int ans = 0;
    dfs(0, root, ans);
    cout << ans << endl;
    return 0;
}

解法二：递归写法建树+自底向上DFS

python

# 题目：【DFS】2023C-悄悄话花费的时间
# 分值：200
# 作者：闭着眼睛学数理化
# 算法：DFS/树（解法二：递归写法建树+自底向上DFS）
# 代码看不懂的地方，请直接在群上提问


# 构建树节点类
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

# 构建树结构的递归函数
def build_tree(idx, nums):
    # 如果idx超过了数组长度，或者在nums中为-1
    # 表示当前是一个空节点，返回None
    if idx >= len(nums) or nums[idx] == -1:
        return None
    # 否则，当前节点node的值为nums[idx]
    # 对idx*2+1和idx*2+2这两个位置进行递归调用
    # 分别为node的左节点和右节点
    # 同时需要将node传回上一层递归
    else:
        node = Node(nums[idx])
        node.left = build_tree(idx*2+1, nums)
        node.right = build_tree(idx*2+2, nums)
        return node

# 自底向上的DFS：从下往上更新路径和
def dfs(node):
    # 遇到空节点，返回0。表示此时空节点对路径和没有贡献。
    if node == None:
        return 0
    else:
        # 计算左节点和右节点递归调用的结果
        # 表示以node.left和node.right为根节点的最大路径和
        left_path_sum = dfs(node.left)
        right_path_sum = dfs(node.right)
        # 在两者中选择较大值，作为以当前节点node为根节点的最大路径和
        path_sum = max(left_path_sum, right_path_sum) + node.val
        return path_sum


nums = list(map(int, input().split()))
# 构建二叉树，返回根节点
root = build_tree(0, nums)
# 递归调用入口，传入root
ans = dfs(root)
print(ans)

java

import java.util.Scanner;

class Node {
    int val;
    Node left, right;

    public Node(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

public class Main {
    public static Node buildTree(int idx, int[] nums) {
        if (idx >= nums.length || nums[idx] == -1) {
            return null;
        }
        Node node = new Node(nums[idx]);
        node.left = buildTree(idx * 2 + 1, nums);
        node.right = buildTree(idx * 2 + 2, nums);
        return node;
    }

    public static int dfs(Node node) {
        if (node == null) {
            return 0;
        }
        int leftPathSum = dfs(node.left);
        int rightPathSum = dfs(node.right);
        int pathSum = Math.max(leftPathSum, rightPathSum) + node.val;
        return pathSum;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String[] numStrings = scanner.nextLine().split(" ");
        int[] nums = new int[numStrings.length];
        for (int i = 0; i < numStrings.length; i++) {
            nums[i] = Integer.parseInt(numStrings[i]);
        }

        Node root = buildTree(0, nums);
        int ans = dfs(root);
        System.out.println(ans);
    }
}

cpp

#include 
#include 
#include 
using namespace std;

class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node(int val) {
        this->val = val;
        left = nullptr;
        right = nullptr;
    }
};

Node* buildTree(int idx, vector<int>& nums) {
    if (idx >= nums.size() || nums[idx] == -1) {
        return nullptr;
    }
    Node* node = new Node(nums[idx]);
    node->left = buildTree(idx * 2 + 1, nums);
    node->right = buildTree(idx * 2 + 2, nums);
    return node;
}

int dfs(Node* node) {
    if (node == nullptr) {
        return 0;
    }
    int leftPathSum = dfs(node->left);
    int rightPathSum = dfs(node->right);
    int pathSum = max(leftPathSum, rightPathSum) + node->val;
    return pathSum;
}

int main() {
    string input;
    getline(cin, input);
    stringstream ss(input);
    vector<int> nums;
    int num;
    while (ss >> num) {
        nums.push_back(num);
    }

    Node* root = buildTree(0, nums);
    int ans = dfs(root);
    cout << ans << endl;
    return 0;
}

时空复杂度

时间复杂度：O(N)。无论是建树还是求最大路径和，均需一次遍历二叉树中的每一个节点。

空间复杂度：O(N)。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多