Acwing算法基础1——快排 归并 二分 前缀和 差分 双指针 位运算 离散化 区间和

流程：

1.理解思想，背模板

2.刷题目

3.重复3~5遍

2021.9.11

1、快排----分治

主要思想：

1.确定分界点：q[l] q[(l+r)/2] q[r] 随机

2.调整范围：x放右边

3.递归：处理左右两端

难点：划分

快排不稳定，如何变得稳定？

将一维数值变成二维的，这样每个数值都不一样，就是稳定的。–>

边界问题：模板

代码思想：两指针同时往中间走，若i指向的数x，指针前移。完成之后指针指向的数swap，继续进行下一次循环

p785 快速排序(acwing)

package one;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

/**
 * @author mys
 *
 * 785.快速排序
 * 给定你一个长度为 n 的整数数列。
 * 请你使用快速排序对这个数列按照从小到大进行排序。
 * 并将排好序的数列按顺序输出。
 */
public class p785_quickSort {
    public static void quickSort(int[] q, int l, int r) {
        //判断边界 注意:要取到=
        if (l >= r) return;
        //取分界点x
        int x = q[(l + r) / 2];
        //定义两个指针的初始位置
        int i = l - 1;
        int j = r + 1;

        //循环迭代
        while (i < j) {
            //分别移动两个指针
            do i++; while (q[i] < x);
            do j--; while (q[j] > x);
            //do Swap
            if (i < j) {
                int temp = q[i];
                q[i] = q[j];
                q[j] = temp;
            }
        }

        quickSort(q, l, j);
        quickSort(q, j + 1, r);

        //i j都可以，注意对称
//        quickSort(q, l, i-1);
//        quickSort(q , i, r);

        //如果选择写i，x不能取q[l],边界问题，会造成死循环;同理，选择j，x不能取到q[r]
        //eg.数组{1，2} x=q[l] 原本排序区间：[0,1];经过第一轮循环之后，还是[0,1]
    }

    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(reader.readLine());

        String[] s = reader.readLine().split(" ");
        int[] a = new int[n];
        for (int i = 0; i < s.length; i++) {
            a[i] = Integer.parseInt(s[i]);
        }

        quickSort(a, 0, n - 1);

        for (int i = 0; i < n; i++) {
            System.out.print(a[i] + " ");
        }
    }
}

思想2：从后往前走，找比x更小的数，放在low位置；

从前往后走，找比x更大的数，放在high位置

当low>=high，一轮循环结束，确定了x的位置，以x为中心，将数组分为左右两边，左右两边的数组继续循环

eg: 5 1 7 3 1 6 9 4 x=5

第一趟：4 1 1 3 5 6 9 7 确定了5；x1=4, x2=6

第二趟：3 1 1 4 5 6 9 7 确定了4，5，6；x1=3, x2=9

第三趟：1 1 3 4 5 6 7 9

2021.9.12

2、归并——分治

主要思想：

1.确定分界点：mid=(l+r)/2

2.递归排序left right

3.归并——合二为一

难点：归并

p787.归并排序

package one;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

/**
 * @author mys
 * @date 2021-9-23 10:53
 *
 * 787.归并排序
 * 给定你一个长度为 n 的整数数列。
 * 请你使用归并排序对这个数列按照从小到大进行排序。
 * 并将排好序的数列按顺序输出。
 */
public class p787_mergeSort {

    /**
     * 归并排序
     * 左右边界：l r
     * 两移动指针：i j,分别指向最左边、最右边的位置
     * @param q
     * @param l
     * @param r
     */
    public static void mergeSort(int[] q, int l, int r) {
        //0.初始条件判断
        if (l >= r) return;

        //1.确定分界点
        int mid = l + r >> 1;

        //2.左右两端递归归并
        mergeSort(q, l, mid);
        mergeSort(q, mid + 1, r);

        //3.调整区间
        int[] tmp = new int[r - l + 1];//开创一个临时数组,存储排好的序
        int k = 0, i = l, j = mid + 1;//tmp数组从0开始，原数组l-r,将原数组分为[l,mid][mid+1,r]
        while (i <= mid && j <= r) {
            //找两端数组中较小的数存放于临时数组tmp
            if (q[i] < q[j]) {
                tmp[k++] = q[i++];
            } else {
                tmp[k++] = q[j++];
            }
        }
        //两端数组中有其中一个剩余，直接加在tmp后面
        while (i <= mid) {
            tmp[k++] = q[i++];
        }
        while (j <= r) {
            tmp[k++] = q[j++];
        }

        //4.最后将tmp返回到原数组
        for (i = l, j = 0; i <= r; i++, j++)
        {
            q[i] = tmp[j];
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        System.out.println("请输入数列长度n:");
        int n = Integer.parseInt(reader.readLine());

        System.out.println("请输入数列：");
        int[] a = new int[n];
        String[] s = reader.readLine().split(" ");
        for (int i = 0; i < n; i ++) {
            a[i] = Integer.parseInt(s[i]);
        }

        mergeSort(a, 0, n - 1);

        for (int i = 0; i < n; i ++) {
            System.out.print(a[i] + " ");
        }
    }
}

2021.9.13

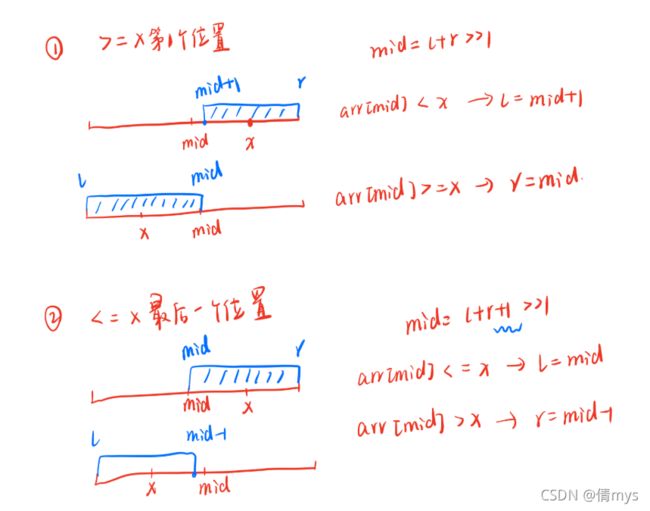
3、二分法

本质并不是单调性，而是找边界点

主要思想：

每次选择答案所在的区间 [l,mid] [mid+1,r]

二分法—整数

p789 数的范围

package one;

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-13 21:12
 *
 * p789 数的范围
 * 给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。
 * 对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。
 * 如果数组中不存在该元素，则返回 -1 -1。
 */
public class p789_dichotomy_integer {
    public static void main(String[] args) {

        System.out.println("请输入数组长度n和询问的次数m:");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int q = in.nextInt();

        System.out.println("请输入数组：");
        int[] arr = new int[n];
        for (int i = 0; i < n; i ++) {
            arr[i] = in.nextInt();
        }

        while(q > 0) {
            q --;

            System.out.println("请输入要询问的x:");
            int k = in.nextInt();

            //第一次查找>=x的第一个位置
            int l = 0;
            int r = n - 1;
            while (l < r) {
                int mid = l + r >> 1;//确定mid位置，根据是前半段还是后半段决定是否+1
                if (arr[mid] < k) {
                    l = mid + 1;//区间：[mid+1, r]
                } else {
                    r = mid;//[l, mid]
                }
            }

            //没找到与x匹配的数
            if (arr[l] != k) {
                System.out.println("-1 -1");
            } else {
                //确定开始位置
                System.out.print(l + " ");
                //第二次查找<=x的最后一个位置
                l = 0;
                r = n - 1;
                while (l < r) {
                    int mid = l + r + 1 >> 1;//在后半段需要+1
                    if (arr[mid] <= k) {
                        l = mid;
                    } else {
                        r = mid - 1;
                    }
                }

                //确定结束位置
                System.out.println(r);
            }
        }
    }
}

789.二分法浮点数

package one;

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-13 21:12
 *
 * 789.浮点数二分法
 * 开平方
 */
public class p789_dichotomy_double {
    public static void main(String[] args) {

        System.out.println("请输入需要开平方的数x:");
        Scanner in = new Scanner(System.in);
        double x = in.nextDouble();

        double l = 0, r = x;
        while (r - l > 1e-8) {
            double mid = (l + r) / 2;
            if (mid * mid >= x) {
                r = mid;
            } else {
                l = mid;
            }
        }
        System.out.println(l);
    }
}

4、高精度（C++）

A+B (lenA = 10^6)、A-B、A*a、A/a

1、大整数存储

数组每位存储一个数字，先存储低位，后存储高位，方便进位时直接在数组最后增加一位；否则就要把所有数往后移一位。

2、大整数运算

用代码模拟手工运算

1.大整数用数组存储 a=“123456” -> A=[6,5,4,3,2,1]

2.四大运算

2021.9.14

5、前缀和(一维、二维）

作用：快速求出数组中某一段数的和

某区间段前缀和计算公式：[l, r] = S[r] - S[l-1]

初始定义：S[0] = 0

一维前缀和

795.前缀和

package one;

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-14 15:05
 *
 * 795.前缀和 一维
 * 输入一个长度为 n 的整数序列。
 * 接下来再输入 m 个询问，每个询问输入一对 l,r。
 * 对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。
 */
public class p795_prefix_first {
    public static void main(String[] args) {
        System.out.println("请输入数组长度n和询问次数m:");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();

        System.out.println("请输入数组：");
        int[] arr = new int[n+1];
        for (int i = 1; i <= n; i ++) {
            arr[i] = in.nextInt();
        }

        int[] s = new int[n+1];
//        s[0] = 0;//初始定义
        //计算前缀和
        for (int i = 1; i <= n; i ++) {
            s[i] = s[i - 1] + arr[i];
        }

        while (m > 0) {
            m --;//询问次数
            System.out.println("请输入区间段l r：");
            int l = in.nextInt();
            int r = in.nextInt();

            //输出某个区间段和
            System.out.print("结果： ");
            System.out.println(s[r] - s[l - 1]);//重要部分
        }
    }
}

二维前缀和

公式可以画图得出：

• 初始化前缀和公式：

  s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1]
  

• 求某段前缀和公式：

  s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]
  

  796.子矩阵的和

package one;

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-14 15:55
 *
 * 796.子矩阵的和
 * 前缀和 —— 二维
 * 初始化前缀和公式：s[i][j] = a[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1]
 * 求某段前缀和公式：s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]
 *
 * 输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。
 * 对于每个询问输出子矩阵中所有数的和。
 */
public class p796_prefix_second {
    public static void main(String[] args) {
        System.out.println("请输入二维数组长n m和询问次数q:");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();

        int[][] a = new int[n + 1][m + 1];
        int[][] s = new int[n + 1][m + 1];

        System.out.println("请输入二维数组：");
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                a[i][j] = in.nextInt();
            }
        }

        //初始化前缀和
//        for (int i = 1; i <= n; i++) {
//            for (int j = 1; j <= m; j++) {
//                s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
//            }
//        }

        //算子矩阵的和
        while (q > 0) {
            q--;
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();

            System.out.println("结果：");
            System.out.println(s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
        }
    }
}

2021.9.15

6、差分(一维、二维）

1.含义：a1,a2...an；构造b1,b2...bn；使得ai = b1+b2+...+bi

2.关系：b1=a1; b2=a2-a1; b3=a3-a2; b4=a4-a3 ... bn=an-an-1

3.重点：a是b的前缀和，b是a的差分

4.作用：对b数组求前缀和得到a数组，只要O(n) b->a

可以只用O(1)给原数组的中间某段全部加上数c

5.案例：一维差分

参考：https://www.acwing.com/solution/content/26588/

• 问题：给定区间[l ,r ]，让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c ,,,,,, a[r] + c

• 步骤：

  1）差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c, a[n] + c;注意：只对b[l]加了c，其他数不变

  理解：b[l]+c相当于a[l]~a[n]都加上c，因为a是b的前缀和，a[l]及其后面的数都包含了b[l]，所以其后所有数都加上了c

  2）b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,a[n] - c

  理解：同上，a[r+1]及其后面需要减去c

• 结论：给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。

797.一维差分

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-15 14:52
 *
 * 一维差分
 *
 * 输入一个长度为 n 的整数序列。
 * 接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。
 * 请你输出进行完所有操作后的序列。
 *
 * 分析：
 * a:原数组    b:a的差分数组   即a是b的前缀和数组，b是a的差分数组
 * 需要在a的[l,r]区间的每个数加上c,等价于b[l]+=c b[r+1]-=c
 */
public class p797_difference {
    public static void main(String[] args) {
        System.out.println("请输入数组长度n和操作次数m:");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();

        System.out.println("请输入数组：");
        int[] a = new int[n + 1];//开辟n+1个空间，因为是从0~n
        for (int i = 1; i <= n; i ++) {
            a[i] = in.nextInt();
        }

        //初始化差分数组
        int[] b = new int[n + 2];//开辟n+2个空间，因为后面会用到b[r+1]，如果r=n，就是b[n+1],0~n+1
        for (int i = 1; i <= n; i ++) {
            b[i] = a[i] - a[i - 1];
    }

        while (m > 0) {
            m --;
            System.out.println("请输入区间l r和加上的数c:");
            int l = in.nextInt();
            int r = in.nextInt();
            int c = in.nextInt();

            //利用结论将序列中[l, r]之间的每个数都加上c
            b[l] += c;
            b[r + 1] -= c;
        }

        //求新的a，即求差分数组b的前缀和数组a
        for (int i = 1; i <= n; i ++) {
            a[i] = b[i] + a[i - 1];
            System.out.print(a[i] + " ");
        }
    }
}

二维差分

计算公式：

b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;

798.差分矩阵

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-15 16:30
 *
 * 二维差分
 *
 * 输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
 * 每个操作都要将选中的子矩阵中的每个元素的值加上 c。
 * 请你将进行完所有操作后的矩阵输出。
 */
public class p798_difference_second {

    public static int[][] b;
    //以(x1,y1)为左上角,(x2,y2)为右下角的区域加上c
    public static void insert(int x1, int y1, int x2, int y2, int c) {
        b[x1][y1] += c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y1] -= c;
        b[x2 + 1][y2 + 1] += c;
    }

    public static void main(String[] args) {
        System.out.println("请输入二维数组行n列m和操作次数q:");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();

        System.out.println("请输入二维数组：");
        int[][] a = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                a[i][j] = in.nextInt();
            }
        }

        //构建差分数组 a是b的前缀和，b是a的差分数组
        b = new int[n + 2][m + 2];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                //相当于b每次加上a[i][j]
                insert(i, j, i, j, a[i][j]);
            }
        }

        //q次操作
        while (q > 0) {
            q --;
            System.out.println("请输入x1 y1 x2 y2 c:");
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();
            int c = in.nextInt();

            //利用结论
            insert(x1, y1, x2, y2, c);
        }

        //计算二维前缀和
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];
            }
        }

        //输出结果
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                System.out.print(b[i][j] + " ");
            }
            System.out.println();
        }
    }
}

BufferReader用法：

    BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out)); 
    
    String[] s1 = reader.readLine().split(" ");
    int n = Integer.parseInt(s1[0]);
    int m = Integer.parseInt(s1[1]);
    int q = Integer.parseInt(s1[2]);
    
    String[] s2 = reader.readLine().split(" ");
	int[] a = new int[n];
	for (int i = 0; i < n; i ++) {
        a[i] = Integer.parseInt(s2[i]);
    }

BufferReader && Scanner

总的来说：BufferReader占用内存更小，速度更快

BufferedReader是支持同步的，而Scanner不支持。BufferedReader的read函数都加了synchronized关键字。

Scanner对输入数据进行正则解析，而BufferedReader只是简单地读取字符序列

7、双指针算法

类型：两个序列；一个序列

模板：

for (int i = 0, j = 0; i < n; i ++) {
	while(j < i && check(i, j)) {
		j ++;
		
		//....
	}
}

作用：O(n^2) —>O(n)

案例：给定一个长度为 n 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

思路：双指针i j，i是遍历指针，j指针用于保证序列 j~i 之间没有重复值，且j尽可能的在序列的最左边的位置

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-16 15:40
 */
public class p799_double_pointer {

    public static int N = 10010;

    public static void main(String[] args) {

        System.out.println("请输入数组长度：");
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();

        System.out.println("请输入数组：");
        int[] a = new int[n];
        for (int i = 0; i < n; i ++) {
            a[i] = in.nextInt();
        }

        //记录序列长度
        int res = 0;
        //记录序列中a[i]的值的个数
        int[] s = new int[N];

        //双指针遍历，i是移动指针，j指针用于保证在序列的最左位置，使得[j,i]之间的序列不重复
        for (int i = 0, j = 0; i < n; i ++) {
            s[a[i]] ++;//a[i]的值个数+1
            //序列中出现重复值，j指针后移
            while (s[a[i]] > 1) {
                s[a[j]] --;//删除序列中j最初指向的值
                j ++;//j指针后移
            }

            //res记录序列的最长长度
            res = Math.max(res, i - j + 1);
        }

        System.out.println(res);
    }
}

8、位运算

1、n的二进制表示中第k位是多少?

1.先把第k位移到最后一位 n>>k

2.看个位是几 x&1

=> n>>k&1

2、lowbit(x)：返回x的最后一位1；可以计算出在二进制下x最后一位1连着后面0的个数的大小

eg.x=10100 lowbit(x)=100

重要公式：x&(-x)

负数是整数的补码：取反+1 eg.-x=~x+1

x&(-x) = x&(~x+1)

x =             1010...100...00

~x=             0101...011...11

~x+1=           0101...100...00

x&(~x+1)=       00...00100...00

作用：求x的1的个数

import java.util.Scanner;

/**
 * @author mys
 * @date 2021-9-18 8:54
 *
 * 二进制位运算
 *
 * 给定一个长度为 n 的数列，请你求出数列中每个数的二进制表示中 1 的个数。
 */
public class p801_bit {

    /**
     * 返回x的最后一位1
     * @param x
     * @return
     */
    public static int lowBit(int x) {
        return x & - x;
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        System.out.println("请输入数列长度n:");
        int n = in.nextInt();

        System.out.println("请输入数组：");
        while (n > 0) {
            n --;
            int x = in.nextInt();
            //记录1的个数
            int res = 0;
            while (x > 0) {
                x -= lowBit(x);//减去x的最后一位1
                res ++;//每次减去x的最后一位1，记录1的个数
            }
            System.out.print(res + " ");
        }
    }
}

9、离散化

1、数组特点：值域大，个数小

eg. 值域0~10^9 个数10^5

[1, 2, 5, … 10^9] ==>[0, 1, …n-1]

2、问题：1）a数组中可能有重复元素 去重

2）如何算出X离散化后的值 二分

C++中去重：

3、离散化原因：存储的数组太大，直接开数组不现实；如果是数轴，采用下标，可能会出现负值；如果用哈希表，不能缩小数组空间

4、离散化关键：将每个数映射成下标。难点是前后映射关系，将不连续的点映射成连续的数组下标

10、区间和

主要思想：有交集——合并

1.按区间左端点排序

2.扫描区间，所有可能有交集的区间合并