最长公共子序列（LCS）_C#

一个序列的子序列是在该序列中删去若干元素后得到的序列。
例：“ABCD”和“BDF”都是“ABCDEFG”的子序列

最长公共子序列（LCS）问题：给定两个序列X和Y，求X和Y长度最大的公共子序列。

 例：X="ABBCBDE" Y="DBBCDB" LCS（X，Y）="BBCD"

直接上递推式

 

C[i，j]表示Xi和Yj的LCS长度

令X=（x1，x2，…，xm）和Y=（1，y2，…，yn）为两个序列，Z=（z1，z2，…，zk）为X和Y的任意LCS。

1.如果Xm=Yn，则Zk=Xm=Yn。且Zk-1是Xm-1和Yn-1的一个LCS。

   比如AB,ACB，X1=Y2=B，LCS最后一位必定是B，且LCS去掉B剩下的一定是A和AC的LCS，也就是A

   LCS的长度满足公式的第二种情况，C[i-1,j-1]+1=1+1=2

2.如果Xm≠Yn，那么Zk不等于Xm，且意味着Z是Xm-1和Y的一个LCS。

   比如ABC，AB，那么LCS最后一位必定不是C,且LCS必定是（X）ABC去掉C=AB和AB的LCS，也就是AB

3.如果Xm≠Yn。那么Zk不等于Zn，且意味着Z是X和Yn-1的一个LCS。

   比如AB，ABC，那么LCS最后一位必定不是C,且LCS必定是（Y）ABC去掉C=AB和AB的LCS，也就是AB

   LCS的长度满足公式的第三种情况，C[i,j-1]或者C[i-1,j]的最大值

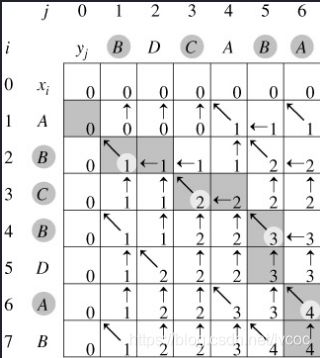
我们可以看下表，更加清楚

 

首先看B和AB，末尾相等，所以LCS长度是C[i-1,j-1]+1，也就是来自左上角+1,0+1=1，表中箭头朝左上角

接着BD和AB，末尾不等，所以LCS长度是C[i,j-1]或者C[i-1,j]的最大值，也就是来自于上边或者左边，表中看到箭头朝左

依次类推

 

    //LCS最长公共子序列
    public int LCS_C(string x,string y)
    {
        char[] X = x.ToArray();
        char[] Y = y.ToArray();
        int m = x.Length;
        int n = y.Length;
        int[,] c = new int[m+1, n+1];//建表,因为有个0，所以长度都要+1
        for (int i = 0; i < m + 1; i++)
        {
            for (int j = 0; j < n + 1; j++)
            {
                c[i, j] = 0;
            }
        }//先初始化表
        for (int i = 1; i < m+1; i++)//行
        {
            for (int j = 1; j < n+1; j++)//列
            {
                //末尾相等,注意表中下标都是+1的，所以拿出去的时候要-1
                if (X[i-1]==Y[j-1])
                {
                    //左上角+1
                    c[i, j] = c[i - 1, j - 1] + 1;
                }
                else
                {
                    //末尾不等
                    //比较左边和上边
                    c[i, j] = Mathf.Max(c[i-1,j],c[i,j-1]);
                }
            }
        }
        return c[m, n];
    }

测试一下哈

 

现在长度可以得到了，但是LCS具体内容呢，还是看表 ，把表复制过来

看图中，注意看深色格子中左上角箭头的就对应LCS的内容 ，因为末尾相等的才会左上角，那么怎么得到这些格子

首先我们要先找出这条路径，很明显的回溯法，从末尾开始往回找，最后一个箭头朝上，找到上一个格子在他上边，然后是左上角，上边，左上角，左边。。。依次，直到到达列表边界停止

那么我们就要保存每一个格子的箭头朝向

 建立一个Grid类，存LCS大小和箭头

    //LCS最长公共子序列 长度和内容
    public Grid[,] LCS_G(string x, string y)
    {
        char[] X = x.ToArray();
        char[] Y = y.ToArray();
        int m = x.Length;
        int n = y.Length;
        Grid[,] c = new Grid[m + 1, n + 1];//建表,因为有个0，所以长度都要+1
        for (int i = 0; i < m + 1; i++)//先初始化表
        {
            for (int j = 0; j < n + 1; j++)
            {
                c[i, j] = new Grid(0, "▦");
            }
        }
        for (int i = 1; i < m + 1; i++)//行
        {
            for (int j = 1; j < n + 1; j++)//列
            {
                //末尾相等,注意表中下标都是+1的，所以拿出去的时候要-1
                if (X[i - 1] == Y[j - 1])
                {
                    //左上角+1
                    c[i, j].C = c[i - 1, j - 1].C + 1;
                    c[i, j].Arrow = "↖";
                }
                else
                {
                    //末尾不等
                    //比较左边和上边
                    if (c[i, j - 1].C>c[i - 1, j].C)
                    {
                        c[i, j].C = c[i, j - 1].C;
                        c[i, j].Arrow = "←";
                    }
                    else if (c[i, j - 1].C <= c[i - 1, j].C)//为了和图表一样，相等优先选择上方
                    {
                        c[i, j].C = c[i - 1, j].C;
                        c[i, j].Arrow = "↑";
                    }
                }
            }
        }
        StringBuilder s = new StringBuilder();
        for (int i = 0; i < c.GetLength(0); i++)
        {
            for (int j = 0; j < c.GetLength(1); j++)
            {
                s.Append((c[i,j].C + c[i, j].Arrow + ","));
            }
            s.Append("\n");
        }
        Debug.Log(s);
        return c;
    }

输出一下GridMap

 

可以和上图中的表对照一下，是一样的，然后我们从最后一格开始回溯 ，遇到左上角箭头就存起来

    public void LCS_FindPath(string x,string y)
    {
        Grid[,] gridMap = LCS_G(x, y);
        int i =x.Length;
        int j=y.Length;
        List res = new List();
        while (i>0&&j>0)
        {
            if (gridMap[i, j].Arrow == "←")
            {
                j -= 1;
            }
            else if (gridMap[i, j].Arrow == "↑")
            {
                i -= 1;
            }
            else if (gridMap[i, j].Arrow == "↖")
            {
                res.Add(x[i-1]);
                   i -= 1;j -= 1;
            }
        }
        res.Reverse();
        StringBuilder s = new StringBuilder();
        foreach (char item in res)
        {
            s.Append(item);
        }
        Debug.Log(s);
    }

 

 测试一下

 

和图表是一样的，也可以试试别的 

 

居然不知不觉过12点了。。。下播了下播了 ,要昏迷了