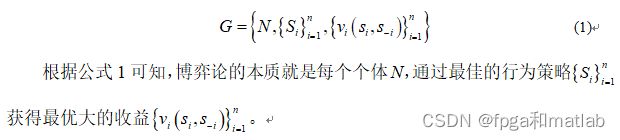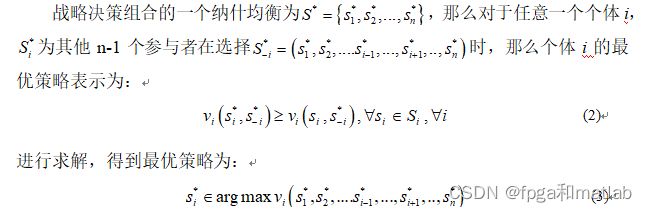纳什均衡和帕累托最优

目录

1.纳什均衡（Nash Equilibrium）

2.帕累托最优（Pareto Optimality）

3.Bertran博弈模型

4.Stackelberg博弈模型

---

         纳什均衡和帕累托最优是博弈论中的两个重要概念，分别描述了多方决策者的最优策略选择情况。让我逐一详细介绍这两个概念：

1.纳什均衡（Nash Equilibrium）

       纳什均衡是博弈论中的一个重要概念，用于描述多方决策者在给定其他决策者的策略情况下，无法通过单方改变自己的策略来获得更好结果的状态。换句话说，每个决策者都选择了对自己最有利的策略，考虑了其他决策者的策略选择。

        具体来说，对于一个博弈中的每个决策者，如果其选择的策略在其他决策者的策略下无法获得更好的支付（效用），则该决策者的策略选择是一个纳什均衡。纳什均衡并不一定是全局最优解，而是在其他决策者策略不变的情况下，各个决策者的最优反应。

2.帕累托最优（Pareto Optimality）

       帕累托最优是一种优化概念，用于描述一种情况下，无法通过改变一个决策者的策略来获得改进，同时保持其他决策者的策略不变。换句话说，帕累托最优是一种状态，其中无法改进一个决策者的结果而不损害其他决策者的结果。

       在帕累托最优状态下，没有办法通过优化来改善一个决策者的情况，而不会对其他决策者的情况造成损害。这种状态体现了一种均衡，其中没有决策者可以单方面获益而不影响其他人。

区别与联系：

• 纳什均衡强调每个决策者在给定其他决策者的策略情况下做出的最优决策，是一个局部性质的均衡概念。
• 帕累托最优强调在无法改进一个决策者的情况下保持其他决策者的策略不变，是一种全局性质的均衡概念。

        尽管两个概念在某些情况下可以相互重叠，但它们在博弈论和优化理论中具有不同的含义和应用。纳什均衡主要用于分析多方互动的决策问题，而帕累托最优主要用于描述在给定约束条件下的最优解。

       在研究非合作博弈中，最为常用的一个评价指标为纳什均衡(Nash equilibrium)。通过纳什均衡可以较好的反应出参与博弈的各个个体的决策和博弈结果。根据纳什均衡的定义可知，采用可以满足纳什均衡的测量，那么最终的博弈结果不仅可以符合个体的自身的收益，也不会损害自己的利益。当任意一个参与博弈的个体知道其他博弈方法都采用符合纳什均衡的策略时，并且都最求利益最大化，那么就可以通过分析知道最终的博弈结果，这个过程即纳什均衡分析法。

        纳什均衡是由纳什在1950年首次提出的，纳什均衡是研究非合作博弈理论的基础。纳什均衡的基本原理中定义了n个参与者个体参与某个博弈，对于某个个体i，在已知其他n-1个参与者的决策之后，个体做出最优决策。那么对于n个个体，所有的个体做出的最优决策的集合构成了一个最优战略组合，这就是纳什均衡的基本概念。纳什均衡是一个平衡的策略组合状态，在纳什均衡中，没有一个博弈参与者能通过改变其决策来获得额外的收益。通过数学方式可以将纳什均衡表示为：

       假设n个博弈可以通过如下表达式来表示：

 

        在实际计算过程中，当博弈参与者数量较多的时候，对组合策略采用逐次验证的方式将变得极其复杂，因此需要根据各个博弈参与者的真实情况，选择最优的纳什均衡计算方法。 

        此外，在博弈论中应用较多的评价指标为帕累托最优，其定义为假设策略S 为帕累托最优策略空间，仅当所有博弈参与者i不存在其他策略S使得满足如下公式：

        即当策略空间中不存在参与者可以不影响其他参与者利益的前提下来提升自身的收益，那么该策略空间即为帕累托最优策略空间。

         纳什均衡是一种平衡状态，其反应了博弈参与者中各个个体未知其他个体的真实决策，而为了自身利益而做出各自的决策，使得博弈结果达到一个平衡状态。而帕累托最优则是假设博弈参与者之间相互合作，做出符合各自最大化利益的决策，帕累托最优属于理想状态下的最优解，但是在实际中并不可能存在。

         目前常见的博弈模型主要包括Cournot古诺博弈模型、Bertran博弈模型、Stackelberg博弈模型等。下面对这几个博弈模型进行介绍。

3.Bertran博弈模型

       Bertrand博弈模型是一种基于完全信息的静态博弈模型，参与Bertrand博弈的所有个体都以定价指标作为其决策变量参数。Bertrand模型最早是由法国人伯特兰德在其发表论文中提出的。根据Bertrand模型的定义可知，其为一个信息透明的竞争模型。在经济学领域中，对于Bertrand博弈模型的理解，我们可以假设存在两家企业，其产品完全相同，生产该产品的成本也相同，其对应的Bertrand均衡是唯一的。那么这两个企业的最终产品价格将同时收敛于实际的边际成本。

       因此，在Bertrand博弈模型中，其均衡的实际含义为两家企业以相同成本生产产品时，其对商品的定价结果都将接近实际的边际成本。而当两个企业的生产成本不一样时，那么最终成本高的企业将被市场淘汰。

        但是Bertrand博弈模型也存在一定的问题，即实际中不同成本的企业，其竞争后的价格并没有降低到边际成本价格上，而是以较高的价格进行销售产品，且获得一定的收益，这个就是Bertrand悖论。

4.Stackelberg博弈模型

       Stackelberg博弈模型是斯坦克尔伯格教授在1934年提出的一种基于双寡头垄断的博弈模型。根据其实现方式来划分，Stackelberg博弈模型分为静态模型和动态模型两种形式。其中静态Stackelberg博弈模型，其博弈参与者分为主体部分和从体部分（在本文所要研究的认知无线电系统中，其博弈参与者的主体为授权用户，从体为认知用户），然后通过预先设定的决策函数获得较好的博弈结果。在静态Stackelberg博弈模型中，由于参与博弈的个体自检信息是相互保密的，因此主体一方具有一定的信息优势，当最后计算博弈策略的时候，选择收益较高的作为最终的博弈决策。而在动态Stackelberg博弈模型，其包含了时间参数，博弈策略将根据主体的特性来计算最优的博弈策略以此达到优化目的，在不同的时刻，其博弈结果将会不同。