代码源每日一题Div.1 (301~307)

301 - 连续子序列

题目链接

简单的动态规划题目，先将所有数进行一个离散化，然后dp。$dp[i]$表示这个位置为结尾的最长符合要求的子序列的长度。对于每一个位置，找这个数对应的离散化编号的上一个数在什么位置，如果那个数目前为止还没有出现，或者那个数与这个数的差不是$1$，$dp[i]=1$；否则设上一个数最后一次出现在$lst$，那么$dp[i]=dp[lst]+1$。

最后选取$dp[i]$最大的中$a[i]$最小的，记$ans$为那个最大的$dp[i]$，$mx$为最大的$dp[i]$中最小的$a[i]$，然后字典序最小的子序列就是$mx-ans+1,\cdots ,mx$。

#include
using namespace std;
typedef long long LL;

int n;
int a[200005], b[200005], c[200005], dp[200005]; 
int lst[200005];
map<int, int> mp;

void main2() {
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		b[i] = a[i];
		lst[i] = 0;
	}
	sort(b + 1, b + n + 1);
	b[0] = 0; int mi = 0;
	for (int i = 1; i <= n; ++i) {
		if (b[i] != b[i - 1]) {
			c[++mi] = b[i];
			mp[b[i]] = mi;
		}
	}
	dp[0] = 0; lst[0] = 0;
	for (int i = 1; i <= n; ++i) {
		int id = mp[a[i]];
		if (id == 1 or !lst[id - 1] or c[id - 1] + 1 != a[i]) {
			dp[i] = 1;
			lst[id] = i;
			continue;
		}
		dp[i] = max(dp[i], dp[lst[id - 1]] + 1);
		lst[id] = i;
	}
	int ans = 0, mx = 0;
	for (int i = 1; i <= n; ++i) {
		if (ans < dp[i]) {
			ans = dp[i]; mx = a[i];
		}
		else if (ans == dp[i]) {
			mx = min(mx, a[i]);
		}
	}
	cout << ans << '\n';
	for (int i = mx - ans + 1; i <= mx; ++i) {
		cout << i << ' ';
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _;
//	cin >> _;
	_ = 1;
	while (_--) main2();
	return 0;
}

302 - 工作安排

题目链接

反悔贪心题目。由于每一个工作的完成时间相同，那么我们每一个时刻都要做一个任务一定是最优的。先将所有任务按照截止时间进行排序，然后按照截止时间从早到晚的顺序进行遍历，如果当前已经完成的任务的数量（也就是已经过去了的时间）超过了这个任务的截止时间，（根据流程会发现，最多也就是超过$1$），那么看已经做的任务里最小价值的任务的价值是否比这个任务的价值高，如果高则不变，如果没有这个任务高，则用这个任务和那个价值最小的任务进行替换。如果已经完成的任务数量小于这个任务的截止时间，那么直接加入完成即可。

用一个小根堆维护所有的利益，每次只需要和小根堆的根进行比较即可。时间复杂度$O(n\log n)$。

#include
using namespace std;
typedef long long LL;

int n;

struct work {
	int d, p;
	bool operator < (const work &x) {
		return p > x.p;
	}
}a[100005];

void main2() {
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i].d >> a[i].p; 
	}
	sort(a + 1, a + n + 1, [](const work &A, const work &B) {
		return A.d < B.d;
	});
	priority_queue<LL> q;
	for (int i = 1; i <= n; ++i) {
		if (a[i].d <= 0) continue;
		if (a[i].d > q.size()) {
			q.push(-a[i].p);
		}
		else if (a[i].p > -q.top()) {
			q.pop();
			q.push(-a[i].p);
		}
	}
	LL ans = 0;
	while (!q.empty()) {
		ans += q.top();
		q.pop();
	}
	cout << -ans;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _;
//	cin >> _;
	_ = 1;
	while (_--) main2();
	return 0;
}

303 - 三角果计数

题目链接

我们发现，如果三个点在一条路径上，那么他们所组成的一定不是三角果。换句话说，想组成三角果，必须长这个样子：

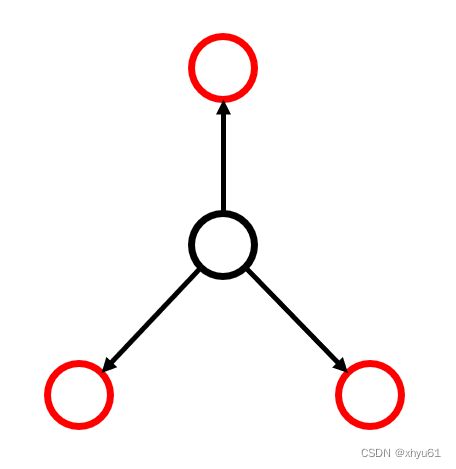
图示属于最简单的情况：三个点分别在三个点之外的一个点（下面称这个点为中心点）的三个分支上，中间可以有别的点。

这样的话我们对于一棵树，枚举每一个顶点，如果这个顶点的分支数不超过$2$，那么这个顶点不会被作为中心点。否则，我们分以下情况讨论：

①如果有一个分支指向这个中心点的父亲结点，那么指向父亲的那个分支有$k$个结点可选。接下来就是下面$x$个子分支。我们设下面这$x$个子结点的编号分别为$a_1,a_2,\cdots ,a_x$，其中$x>1$。我们要从下面这$x$个分支中选择两个分支，从两个分支中各选$1$个点。显然，从下面$x$个分支中选择两个结点的方案数是：
$$S=a_1{a}_2+a_1{a}_3+\cdots +a_1{a}_x+a_2{a}_3+\cdots +a_{x-1}{a}_x$$
枚举$x$比较小时的情况后，我们发现（也可以是推出）：
$$S=\frac{1}{2}\times [(a_1+a_2+\cdots +a_x{)}^2-(a_1^2+a_2^2+\cdots +a_x^2)]$$
又有$k=n-sz[u]$，其中$sz[u]$表示这个中心点为根的子树的大小。所以这种情况可以选取的三个符合要求的点的点数是$(n-sz[u])\times S$。

②如果三个分支都指向子结点，那么就是从下面$x$个分支中选择$3$个分支，每个分支选择一个点的所有可能情况。同样设这$x$个子结点的编号分别为$a_1,a_2,\cdots ,a_x$，其中$x>2$。显然，这种选择的方案数是：
$$S=a_1{a}_2{a}_3+a_1{a}_2{a}_4+\cdots +a_1{a}_2{a}_x+a_1{a}_3{a}_4+\cdots a_{x-2}{a}_{x-1}{a}_x$$
同样枚举$x$比较小时的情况后，我们发现（当然也可以是推出）：
$$T=a_1+a_2+\cdots +a_x$$
将$T$带入下式
$$S=\frac{1}{6}\times [T^3-3a_1^2\times (T-a_1)-3a_2^2\times (T-a_2)-\cdots -3a_x^2\times (T-a_x)-(a_1^3+a_2^3+\cdots +a_n^3)]$$

对于一个结点，求出这两种情况的方案数总和。我们从根结点开始dfs整棵树，对每一个结点都算一个答案，最后做和即为这道题目的最终答案。

#include
using namespace std;
typedef long long LL;

int n, en = 0;
LL front[100005], sz[100005];
LL ans = 0;

struct Edge {
	LL v, w, next;
}e[200005];

void addEdge(int u, int v, int w) {
	e[++en] = {v, w, front[u]};
	front[u] = en;
}

void dfs0(int u, int fa) {
	sz[u] = 1;
	for (int i = front[u]; i; i = e[i].next) {
		int v = e[i].v;
		if (v == fa) continue;
		dfs0(v, u);
		sz[u] += sz[v];
	}
}

void dfs(int u, int fa) {
	LL s1 = 0, s2 = 0, s3 = 0, s4 = 0, cnt = 0;
	for (int i = front[u]; i; i = e[i].next) {
		int v = e[i].v;
		if (v == fa) continue;
		++cnt;
		s1 += sz[v]; s2 += (sz[v] * sz[v]);
		s3 += sz[v] * sz[v] * sz[v];
		s4 += ((sz[v] * sz[v]) * (sz[u] - sz[v] - 1));
		dfs(v, u);
	}
	ans += ((LL)(n - sz[u]) * (s1 * s1 - s2) / 2);
	if (cnt >= 3) ans += ((s1 * s1 * s1 - s3 - 3 * s4) / 6);
}

void main2() {
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		front[i] = 0;
	}
	for (int i = 1; i < n; ++i) {
		int u, v, w;
		cin >> u >> v >> w;
		addEdge(u, v, w); addEdge(v, u, w); 
	}
	dfs0(1, 0);
	dfs(1, 0);
	cout << ans << '\n';
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _;
//	cin >> _;
	_ = 1;
	while (_--) main2();
	return 0;
}

304 - 整齐的数组2

题目链接

如果序列中的两个数$x,y$，满足减去$k$的倍数后相等，那么意味着$x-ak=y-bk$，即$x\mathrm{mod}k=y\mathrm{mod}k$。也就是说，满足条件的$k$，意味着对于所有的$a[i]\mathrm{mod}k$，存在一个$x$使得满足$a[i]\mathrm{mod}k=x$的$i$的数量大于等于$n$的一半。

现在考虑什么样的$k$是满足条件的：显然，对于$x-ak=y-bk$，我们有$x-y=(x-b)k$，也就是说，任意两个数的差值都有可能是$k$的倍数。所以我们求出所有可能的差值的绝对值，并枚举每一个差值的绝对值的因数，将这个数作为$k$，去看这个$k$是否满足条件即可。

时间复杂度$O(n^2\sqrt{n})$。

#include
using namespace std;
typedef long long LL;

int n, k;
int a[55];
set<int> s;

bool check(int x) {
	map<int, int> mp2;
	for (int i = 1; i <= n; ++i) {
		int y = (a[i] % x + x) % x;
		++mp2[y];
		if (mp2[y] >= n / 2) return true;
	}
	return false;
}

void main2() {
	cin >> n;
	k = 0;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
	}
	map<int, int> mp1;
	for (int i = 1; i <= n; ++i) {
		if (!mp1[a[i]]) mp1[a[i]] = 1;
		else mp1[a[i]]++;
		if (mp1[a[i]] >= n / 2) {
			cout << -1 << '\n';
			return;
		}
	}
	s.clear();
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= n; ++j) {
			if (a[i] != a[j]) {
				s.insert(abs(a[i] - a[j]));
			}
		}
	}
	map<int, int> mp;
	for (int x: s) {
		for (int i = 1; i * i <= x; ++i) {
			if (x % i != 0) continue;
			if (!mp[i] and check(i)) {
				k = max(k, i);
			}
			mp[i] = 1;
			if (!mp[x / i] and check(x / i)) {
				k = max(k, x / i);
			}
			mp[x / i] = 1;
		}
	}
	cout << k << '\n';
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _;
	cin >> _;
//	_ = 1;
	while (_--) main2();
	return 0;
}

305 - 三进制循环

题目链接

我们发现，一个路径上至多会出现一个拐点，这个拐点满足一侧是从上到下点权取模意义下递增，一侧从上到下点权取模意义下递减。那么走两次dfs，一次计算这个点分支里从上到下点权取模意义下递增的最长路径$dp1[u]$，一次计算这个点分支里从上到下点权取模意义下递增的最短路径$dp2[u]$，对于每一个结点$u$，其答案是$dp1[u]+dp2[u]+1$。取所有点的答案的最大值，即为所求。

#include
using namespace std;
typedef long long LL;

const int N = 500005;

int n, en = 0;
int front[N], dp1[N], dp2[N], c[N];

struct Edge {
	int v, next;
}e[N * 2];

void addEdge(int u, int v) {
	e[++en] = {v, front[u]};
	front[u] = en;
}

void dfs1(int u, int fa) {
	for (int i = front[u]; i; i = e[i].next) {
		int v = e[i].v;
		if (v == fa) continue;
		dfs1(v, u);
		if (c[v] == (c[u] + 1) % 3) {
			dp1[u] = max(dp1[u], dp1[v] + 1);
		}
	}
}

void dfs2(int u, int fa) {
	for (int i = front[u]; i; i = e[i].next) {
		int v = e[i].v;
		if (v == fa) continue;
		dfs2(v, u);
		if (c[u] == (c[v] + 1) % 3) {
			dp2[u] = max(dp2[u], dp2[v] + 1);
		}
	}
}

void main2() {
	cin >> n;
	for (int i = 1; i < n; ++i) {
		int u, v;
		cin >> u >> v;
		addEdge(u, v); addEdge(v, u);
	}
	for (int i = 1; i <= n; ++i) {
		dp1[i] = dp2[i] = 0;
		cin >> c[i];
	}
	dfs1(1, 0); dfs2(1, 0);
	int ans = 0;
	for (int i = 1; i <= n; ++i) {
		ans = max(ans, dp1[i] + dp2[i] + 1);
	}
	cout << ans;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _;
//	cin >> _;
	_ = 1;
	while (_--) main2();
	return 0;
}

306 - 树上逆序对

题目链接

对于每一个$k$，我们发现我们能够枚举的有子结点的数量是与$\frac{1}{k}$成正相关的，所以枚举$k$的每一个可能的结点的时间复杂度是$O(n\log n)$的。对于每一个有子结点的结点$i$，相当于统计数列中$[k(i-1)+2,ki+1]$的范围内，小于$a_i$的数有多少。这个题和每日一题108 数数是一样的。每一个查询是$O(\log n)$的，所以整体的时间复杂度是$O(n(\log n{)}^2)$。

线段树常数略大，推荐用树状数组。

#include
using namespace std;
typedef long long LL;

int n;
int a[200005], b[200005], res[200005];

struct QUERY {
	int l, r, h, k, ans;
};

vector<QUERY> q;
vector<int> id[200005];
map<int, int> mp;

int c[200005];

int lowbit(int x) {
	return x & (-x);
}

void add(int x, int k) {
	while (x <= n) {
		c[x] += k; x += lowbit(x);
	}
}

int presum(int x) {
	int ans = 0;
	while (x >= 1) {
		ans += c[x]; x -= lowbit(x);
	}
	return ans;
}

void main2() {
	cin >> n;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		b[i] = a[i];
		res[i] = 0;
	}
	sort(b + 1, b + n + 1);
	b[0] = 0;
	int mi = 0;
	for (int i = 1; i <= n; ++i) {
		if (b[i] != b[i - 1]) {
			mp[b[i]] = ++mi;
		}
	}
	for (int i = 1; i <= n; ++i) {
		a[i] = mp[a[i]];
		id[a[i]].push_back(i);
	}
	for (int k = 1; k <= n - 1; ++k) {
		for (int i = 1; ; ++i) {
			int l = k * (i - 1) + 2, r = k * i + 1;
			if (l > n) break;
			q.push_back({l, min(n, r), a[i], k, 0});
		}
	}
	sort(q.begin(), q.end(), [](const QUERY &A, const QUERY &B) {
		return A.h > B.h;
	});
	for (int i = 1; i <= n; ++i) {
		add(i, 1);
	}
	int lst = mi + 1;
	for (QUERY &x: q) {
		if (lst > x.h) {
			for (int i = lst - 1; i >= x.h; --i) {
				for (int y: id[i]) {
					add(y, -1);
				}
			}
			lst = x.h;
		}
		x.ans = presum(x.r) - presum(x.l - 1);
		res[x.k] += x.ans;
	}
	for (int i = 1; i < n; ++i) {
		cout << res[i] << ' ';
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	LL _;
//	cin >> _;
	_ = 1;
	while (_--) main2();
	return 0;
}

307 - 约分

题目链接

题目中给定的$a,b$都是long long范围内的，所以在十进制当中不会超过20位。我们枚举分子所有可能的取数方式，将$a$的这些数位剔除后变成$p$。理想状态下，我们有$\frac{a}{b}=\frac{p}{q}$，变形得到$q=\frac{pb}{a}$。如果取走数位后得到的$q$是一个正整数，那么我们看相比于$q$和$b$，从$b$中取走相同的数位是否可以形成$q$。如果可以形成$q$，那么这种方式就可以，更新答案为更小的$p$。

时间复杂度$O(19\times 2^{19})$。

#include
using namespace std;
typedef __int128 LL;

LL p, q, lp, lq, pt, qt;
LL ti, t2, X, Y;
LL dig_p[32], dig_q[32];
LL dtot[12];
LL tmp[12];
map<LL, LL> mp;

inline LL read()
{
	LL x=0,w=1; char c=getchar();
	while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
	while(c<='9'&&c>='0') x=(x<<1)+(x<<3)+c-'0',c=getchar();
	return w==1?x:-x;
}

inline void write(LL x)
{
	if(x>=10) write(x/10);
	putchar(x%10+'0');
}

pair<LL, LL> dfs(LL sta, LL T) {
	if (T == ti + 1) {
		Y = 0;
		for (LL i = qt - 1; i >= 0; --i) {
			if ((sta & (1ll << i)) == 0) {
				Y = Y * 10 + dig_q[i];
			}
		}
		if (Y == 0) return {-1, -1};
		double NEW_D = (double)X / (double)Y;
		double ORI_D = (double)lp / (double)lq;
		if (fabs(NEW_D - ORI_D) < 1e-6) {
			return {X, Y};
		}
		else return {-1, -1};
	}
	for (LL i = 0; i < qt; ++i) {
		if (dig_q[i] == dig_p[tmp[T]] and (sta & (1ll << i)) == 0) {
			pair<LL, LL> tpp = dfs((sta | (1LL << i)), T + 1);
			if (tpp.first != -1) return tpp;
		}
	}
	return {-1, -1};
}

pair<LL, LL> check2(LL st) {
	ti = t2 = 0; LL ten = 1;
	X = 0;
	for (LL i = 0; i < 10; ++i) tmp[i] = 0;
	for (LL i = 0; i < pt; ++i) {
		if ((st & (1ll << i)) == 0) {
			X += (dig_p[i] * ten);
			ten *= 10;
		}
		else tmp[++ti] = i;
	}
	if (mp[X]) return {-1, -1};
	mp[X] = 1;
	pair<LL, LL> chk = dfs(0, 1);
	if (chk.first != -1) {
		return chk;
	}
	else return {-1, -1};
}

pair<LL, LL> check(LL st) {
	LL dd[12]; X = 0; LL ten = 1;
	for (LL i = 0; i < 10; ++i) {
		dd[i] = tmp[i] = dtot[i];
		
	}
	for (LL i = 0; i < pt; ++i) {
		if ((st & (1ll << i)) == 0) {
			X += (dig_p[i] * ten);
			ten *= 10;
		}
		else tmp[dig_p[i]]--;
	}
	Y = (X * lq) / lp;
	if (Y == 0 or (X * lq) % lp != 0) return {-1, -1};
	LL yy = Y;
	while (yy) {
		tmp[yy % 10]--; yy /= 10;
	} 
	for (LL i = 1; i < 10; ++i) {
		if (tmp[i] > 0) return {-1, -1};
	}
	if (tmp[0] < 0) return {-1, -1};
	LL res[32]; LL ri = 0; yy = Y;
	while (yy) {
		res[ri++] = yy % 10; yy /= 10;
	}
	for (LL i = 1; i <= tmp[0]; ++i) {
		res[ri++] = 0;
	}
	LL rpt = 0;
	for (LL i = 0; i < qt; ++i) {
		if (dig_q[i] == res[rpt]) ++rpt;
		if (rpt == ri) return {X, Y};
	}
	return {-1, -1};
}

void main2() {
	p = read(); q = read();
	mp.clear();
	while (p % 10 == 0 and q % 10 == 0) {
		p /= 10; q /= 10;
	}
	LL xp = p, xq = q, G = __gcd(p, q); 
	pt = 0; qt = 0;
	lp = p / G; lq = q / G; 
	while (xp) {
		dig_p[pt++] = xp % 10;
		xp /= 10;
	}
	while (xq) {
		dig_q[qt++] = xq % 10;
		xq /= 10;
	}
	
	memset(dtot, 0, sizeof(dtot));
	for (LL i = 0; i < qt; ++i) {
		dtot[dig_q[i]]++;
	}
	pair<LL, LL> ans = {-1, -1};
	for (LL i = 0; i < (1ll << pt); ++i) {
		LL dpp[12]; LL del_ok = 1; 
		for (LL j = 0; j < pt; ++j) {
			if ((i & (1ll << j)) > 0) ++dpp[dig_p[j]];
		}
		for (LL j = 0; j < 10; ++j) {
			dpp[j] = 0;
		}
		for (LL j = 0; j < 10; ++j) {
			if (dpp[j] > dtot[j]) {
				del_ok = 0;
				break;
			}
		}
		if (!del_ok) continue;
		pair<LL, LL> tpi = check(i);
		if (tpi.first != -1) {
			if (ans.first == -1) ans = tpi;
			else if (ans.first > tpi.first) ans = tpi; 
		}
	}
	write(ans.first); printf(" ");
	write(ans.second); printf("\n");
}

int main() {
	LL _; _ = 1;
	while (_--) main2();
	return 0;
}