二叉树OJ题目（2）

目录

1.二叉树的深度 

2.单值二叉树

3.二叉树的前序遍历

4.二叉树的中序遍历

5.二叉树的后序遍

---

• 题目目代码
• 思路整体分析&注意事项
• 易错点
• 画图递归分析

1.二叉树的深度 

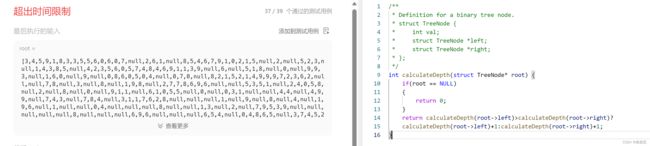
LCR 175. 计算二叉树的深度 - 力扣（LeetCode）https://leetcode.cn/problems/er-cha-shu-de-shen-du-lcof/description/

int calculateDepth(struct TreeNode* root) {
    if(root == NULL)
    {
        return 0;
    }
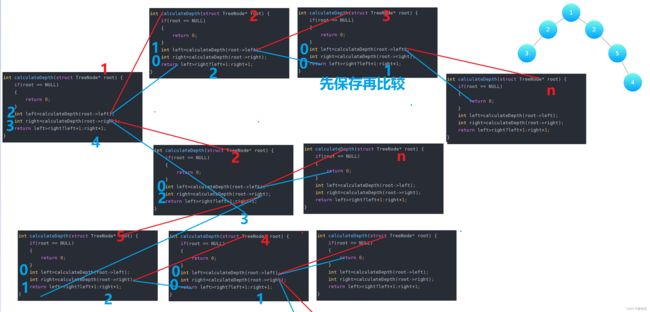
    int left=calculateDepth(root->left);
    int right=calculateDepth(root->right);
    return left>right?left+1:right+1;
}

//❌
int calculateDepth(struct TreeNode* root) {
    if(root == NULL)
    {
        return 0;
    }
    return calculateDepth(root->left)>calculateDepth(root->right)?
    calculateDepth(root->left)+1:calculateDepth(root->right)+1;
}

• 分治思想：根的高度（1）+左右子树高的一棵

  ---

  易错点

• 需要保存之后再比较。不然会多次调用，超出时间限制❗❗

2.单值二叉树

965. 单值二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/univalued-binary-tree/description/

/**
 * Definition for a binary tree node.                          
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
    {
        return true;
    }

    if(root->left != NULL )
    {
        if(root->val != root->left->val)
        {
            return false;
        }
    }
    if(root->right != NULL )
    {
        if(root->val != root->right->val)
        {
            return false;
        }
    }
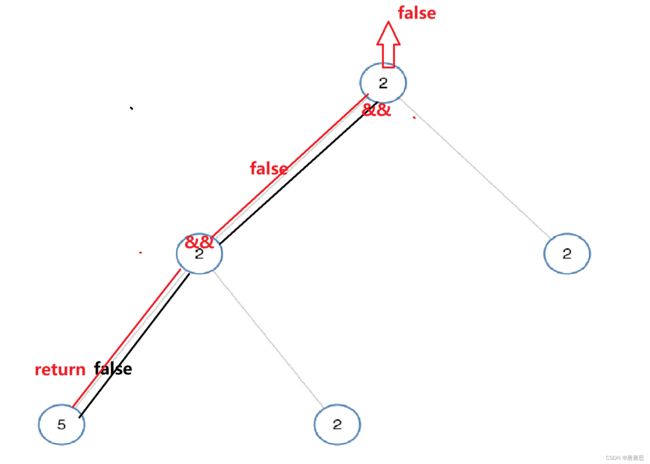
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
    //相等往下走且返回
}

一棵树的所有节点都有相同的值，当且仅当对于树上的每一条边的两个端点，它们都有相同的值（这样根据传递性，所有节点都有相同的值）。因此，我们可以对树进行一次深度优先搜索。当搜索到节点 xxx 时，我们检查 xxx 与 xxx 的每一个子节点之间的边是否满足要求。

例如对于左子节点而言，如果其存在并且值与 xxx 相同，那么我们继续向下搜索该左子节点；如果值与 xxx 不同，那么我们直接返回 False

• 分治的思想：检查每个节点和他的左右孩子

• 若为空树就返回true

• 若左孩子不为空，比较值不一样就返回false

• 若右子树不为空，比较值不一样就返回false

• 比较完根和左右孩子，递归下去左右子树走上诉相同的逻辑

• 若两边树所有值遍历完都一样，才返回true

  ---

  易错点

• && 都为true才返回true

• != 是因为只要一个节点元素值不一样就返回false，不能通过确定一个节点元素值一样就返回true（逻辑思维）

          if(root->val != root->right->val)
          {
              return false;
          }
  
          if(root->val == root->right->val)
          {
              return true;//❌
          }
  //比较

3.二叉树的前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-preorder-traversal/description/

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}

int *preorder(struct TreeNode* root,int*a,int* pi)
{
    if(root == NULL)
    {
        return NULL;
    }
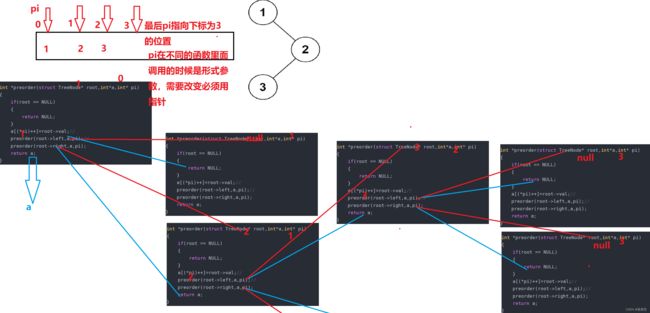
    a[(*pi)++]=root->val;//
    preorder(root->left,a,pi);//
    preorder(root->right,a,pi);
    return a;
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int treesize=TreeSize(root);
    *returnSize=treesize;
    int*a=(int*)malloc(sizeof(struct TreeNode)*treesize);
    int i=0;
    a=preorder(root,a,&i);
    i=0;
    return a;
}

• 题目要求：开辟数组，把遍历树的顺序放入数组即可。 
• 计算树的节点个数
• malloc节点个数的空间
• 前序：根左右
• 把根的val放入数组第一个元素
• 接着放入左右（递归下去）

  ---

  易错点

• 改变形式参数必须要用指针！！！（&i）

• 形参是实参的一份临时拷贝

• int* returnSize 这个是返回数组的元素个数（*代表leetcode后台有一份returnsize的实际参数需要改变用的指针&returnsize，这里才用指针接收）

4.二叉树的中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-inorder-traversal/description/

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}

int *inorder(struct TreeNode* root,int*a,int* pi)
{
    if(root == NULL)
    {
        return NULL;
    }
    inorder(root->left,a,pi);//
    a[(*pi)++]=root->val;//
    inorder(root->right,a,pi);
    return a;
}

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int treesize=TreeSize(root);
    *returnSize=treesize;
    int*a=(int*)malloc(sizeof(struct TreeNode)*treesize);
    int i=0;
    a=inorder(root,a,&i);
    i=0;
    return a;
}

5.二叉树的后序遍

145. 二叉树的后序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-postorder-traversal/description/

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left)+TreeSize(root->right)+1;
}

int *postorder(struct TreeNode* root,int*a,int* pi)
{
    if(root == NULL)
    {
        return NULL;
    }
    postorder(root->left,a,pi);//
    postorder(root->right,a,pi);
    a[(*pi)++]=root->val;//
    return a;
}

int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    int treesize=TreeSize(root);
    *returnSize=treesize;
    int*a=(int*)malloc(sizeof(struct TreeNode)*treesize);
    int i=0;
    a=postorder(root,a,&i);
    i=0;
    return a;
}

6.二叉树的构建及其遍历

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

感谢大家的阅读，若有错误和不足，欢迎指正