算法导论 总结索引 | 第一部分 第二章：算法基础

1、插入排序（24）

1、希望排序的数 也称为关键词

2、插入排序 对于少量排序元素，是一个 有效的算法

3、原址排序输入的数：算法在 数组A中 重排这些数，在 任何时候，最多只有 其中的常数个数字 存储在数组外面

注意下标是从1开始的，从第2个数字开始向后的每个数 向前插入到 当前正确位置，确保 插入数字 及 之前的数字 从小到大排列

1.1 循环不变式 与 插入排序的正确性

1、对于 for循环（循环变量为j）中的 每次迭代开始，剩余子数组 A[j+1…n]待排

元素A[1…j-1] 就是 原来位置 1到 j - 1 的元素，且 已经按序排列，把A[1…j - 1]的这些性质 形式地表示为一个 循环不变式

2、循环不变式 来帮助理解 算法的正确性。循环不变式 必须证明三条性质：
1）初始化：循环的第一次迭代之前，为真
2）保持：如果 循环的某次迭代之前 它为真，下次迭代之前 它仍为真
3）终止：循环终止时，不变式 提供一个有用的性质，该性质 有助于证明算法是 正确的

类似于 数学归纳法
通常 和导致循环终止的条件 一起使用循环不变式。终止性 不同于 通常数学归纳法中 对归纳步的无限使用，这里当循环终止时，停止 归纳

3、对于 插入排序 使用 循环不变式理解 其正确性
1）初始化
证明在第一次循环之前（j = 2），循环不变式 成立，子数组 A[1…j - 1]仅由 单个元素A[1]组成
实际上 就是A[1]中原来的元素，该子数组是排列好的
即第一次循环之前 循环不变式成立

2）保持
非形式化地证明每次迭代 保持 循环不变式
最后将 A[j]的值插入位置时，这时 子数组A[1…j] 由原来在A[1…j]中的元素组成，且 已按序排列
即 对for循环的下一次迭代增加j将 保持循环不变式

3）终止
最后研究在 循环终止时 发生了什么。导致for循环终止的条件是 j > A.length = n，最后j = n + 1，将 循环不变式的表述中 将j用n+1代替，于是有：子数组A[1…n]由原来在A[1…n]中的元素组成，且 已按序排列
而A[1…n]就是整个数组，推断出整个数组已排序，因此 算法正确

1.2 伪代码中的约定（26）

1、A[i]表示数组A的 第i个元素，不从0开始

2、表示一个数组 或 对象的变量 看作指向表示数组 或 对象的数据 的一个指针。对于 某个对象 x 的所有属性f，赋值 y = x 导致 y.f 等于 x.f。现在置x.f = 3，则赋值后不但 x.f 等于3，而且 y.f 也等于3

3、一个指针 不指向任何对象，赋给它特殊值NIL

4、布尔运算符"and" 和 “or” 都是短路的
即："x and y"先求值 x，如果 x 求值为 false，不再求值y；类似的，"x or y"仅当x求值为false时，才求值 表达式y

1.3 练习

1、按非升序排序（而不是非降序）的过程INSERTION-SORT：
和降序的唯一区别 就是 在while的第二个条件判断

INSERTION-SORT(A)
    for j = 2 to A.length
        key = A[j]
        // Insert A[j] into the sorted sequence A[1..j - 1].
        i = j - 1
        while i > 0 and A[i] < key
            A[i + 1] = A[i]
            i = i - 1
        A[i + 1] = key

2、输入： 代表n位二进制整数的两个n元数组A和B
输出： (n+1)元数组C使得C代表的二进制整数等于A和B代表的两个二进制整数之和

ADD-INTEGER(A, B)
    key = 0
    for i = 1 to n
        C[i] = (A[i] + B[i] + key) mod 2
        key = ⌊(A[i] + B[i] + key) / 2⌋
    C[n + 1] = key
    return C

二进制加法，单个位上 最多1+1+1（最后一个1是进上来的）不会超过3

2、分析算法（28）

1、假定一种通用的单处理器计算模型 —— 随机访问机（RAM）来作为 我们的实现技术，在RAM模型中，指令 一条接一条地执行

2、输入规模 的最佳概念 依赖于研究的问题。一个算法在 特定输入上的运行时间 是指执行的基本操作数 或步数
for / while 循环按通常方式 退出的时候，执行测试的次数 比 执行循环体的次数 多1
对于 每次for循环（循环变量为j）执行while的次数为 tj

需要执行Ci步 且执行n此的一条语句 将贡献Ci*n 给总运行时间，将 代价与次数列 对应元素之积求和

3、即使对 给定规模的输入，一个算法的运行时间 也可能依赖于 给定的是 该规模下的哪个输入。在插入算法中，若 输入数组已排好序，则出现 最佳情况
第6，7步 不会执行，第五步对于每个for循环 只会执行 一次（第一次判断，t5 == 1）。最佳情况的运行时间为

可以把 该运行时间 表示为an+b，常量a 和 b 依赖于语句代价ci，因此其为 n的线性函数

若输入数组 已反向排序，则导致最坏情况：每个元素A[j] 与 整个已排序子数组A[1…j - 1]中的每个元素 进行比较，再加上while对每个数的判断 都要多一次，所以对于 j = 2, 3, … , n, 有tj = j（1, 2, … , n），所以
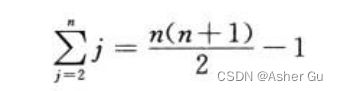（等差数列求和 2, … , n；先算1, 2, …, n 再减1）

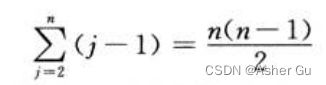
最坏情况下的运行时间为

可以把 该运行时间 表示为an² + bn + c，常量a, b 和 c 依赖于语句代价ci，因此其为 n 的 二次函数

4、虽然 以后会看到 随机化算法，即使对 固定的输入，其行为 也可能变化，但通常的情况 就像插入排序那样，算法的运行时间 对 给定的输入是 固定的

5、往往集中于 只求最坏情况运行时间
1）一个算法的最坏情况运行时间 给出了任何输入的运行时间的上界
2）对某些算法，最坏情况经常出现。如：当在数据库中 检索一条特定消息时，若 该信息不在数据库中 出现，则 检索算法的最坏情况 会经常出现）
3）平均情况往往与最差情况 一样差。如：插入排序tj大概是j / 2，也是输入规模的二次函数

6、对 无法用平均情况分析的（不是给定规模的所有输入 具有相同的可能性），可以使用 随机化算法，它做出随机的选择，以允许 进行概率分析 并产生某个期望运行时间

7、增长量级：真正感兴趣的是 运行时间的增长率 或 增长量级。所以 只考虑公式中 最重要的项（例如an²），当n的值很大时，低阶项 相对来说不太重要。同时也忽略 最重要的项的常系数，因为 对大的输入，在确定计算效率时 常量因子 不如增长率重要
记插入排序 具有最坏情况运行时间 Θ(n²)

8、选择算法：考虑排序存储在 数组A中的n个数，首先找出A中的最小元素 并将其与 A[1]中的元素 进行交换，接着，找出 A中的次小元素 并将其与A[2]中的元素 进行交换。对A中前n - 1个元素 按该方式继续

SELECT-SORT(A)
    for i = 1 to A.length - 1
        smallest = i
        for j = i + 1 to A.length
            if A[j] < A[smallest]
                smallest  = i
        exchange A[i] with A[smallest]

循环不变式：在第2~5行的for循环的每次迭代开始时，A[i - 1]是数组中第i - 1小的元素

3、设计算法（31）

算法设计技术 包括
1）增量方法：如插入排序，在排序子数组A[1…j - 1] 后，将 单个元素A[j] 插入子数组的适当位置，产生排序好的子数组A[1…j]
2）分治法：使用分治法设计的 排序算法 的最坏情况运行时间 比 插入排序要少得多。分治算法的优点之一 是使用第四章介绍的技术 很容易确定其运行时间

3.1 分治法（归并排序）

1、很多有用的算法 结构上是 递归的，算法 一次或多次 递归地调用自身 以解决紧密相关的若干子问题

典型地遵循分治法的思想：将原问题 分解为 几个规模较小但 类似于原问题的子问题，递归地求解 这些子问题，然后再 合并这些子问题 来建立原问题的解

2、分治模式 在每层递归的时候 都有三个步骤：
分解 原问题为 若干子问题，这些子问题是 原问题的规模较小的实例
解决 这些子问题，递归地求解各子问题。若子问题的规模足够小，则 直接求解
合并 这些子问题的解 成原问题的解

3、归并排序算法 就是 分治模式
分解：分解待排序的n个元素的序列 成各具 n / 2 个元素的两个 子序列
解决：使用 归并排序 递归地排序两个子序列
合并：合并两个 已排序序列（关键步骤）
当 待排序的序列 长度为1时，递归 开始回升

合并：每次都拿两个序列里面 更小的，一个序列空了后 直接接上另一个序列
为了避免序列先空，放置哨兵牌（无穷大）

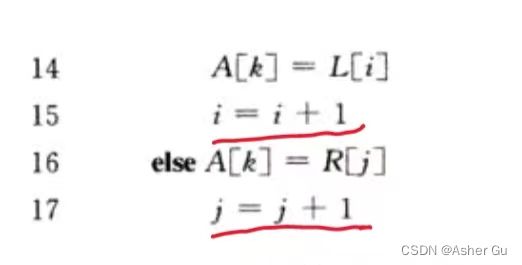
完整函数

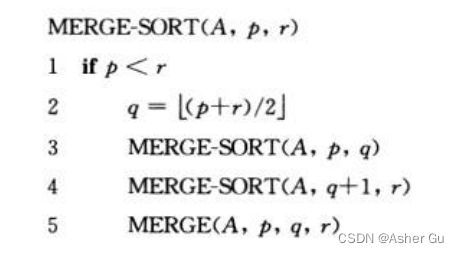
4、可以使用 循环不变式 证明正确性
循环不变式：(k为 for循环中的k, n1、n2为伪代码8, 9行中的n1, n2)
子数组A[p…k - 1] 包含 L和R的 k - p个最小元素，L[i] 和 R[j] 都是 各自所在数组中 没被复制回 数组A 的最小元素

1）初始化：k = p，空子数组A[p…k - 1] 包含 L和R的 k - p = 0个最小元素，L[i] 和 R[j] 都是 各自所在数组中 没被复制回 数组A 的最小元素

2）保持：每次迭代 都维持循环不变式，分 L[i] <= R[j] 以及 L[i] > R[j] 两种情况

3）终止：终止时k = r+1。根据循环不变式，子数组A[p…k - 1]就是 A[p…r] 且按 从小到大的顺序包含L[1…n1+1] 和 R[1…n2+1]中的 k - p = r - p + 1个最小元素，除两个 最大元素外（哨兵），其他元素 都已被复制回数组A

5、整个递归过程

3.2 分析分治算法

1、算法包含 对自身的递归调用时，可以用 递归方程 或 递归式 来描述其运行时间。假设 T(n) 是规模为n的一个问题的运行时间，把原问题分为 a个子问题，每个子问题的规模是原问题的 1 / b（归并排序 a = b = 2，但很多时候 a != b）需要 aT(n/b) 的时间 来求解a个子问题

如果分解问题成 子问题需要时间 D(n)，合并子问题的解 需要时间 C(n)

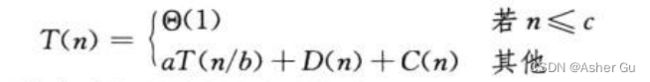
2、归并排序算法分析（35）
假设原问题规模 是2的幂，将简化递归式的分析，且这个假设 不影响 递归式解的增长量级
分解：仅仅计算 子数组的中间位置 D(n) = Θ(1)
解决：递归地求解 两个规模均为 n/2 的子问题，运行时间 2T(n/2)
合并：在一个具有n个元素的子数组上 合并两个子数组 需要 Θ(n) 的时间，所以 C(n) = Θ(n)

把一个 Θ(n) 函数 与另一个 Θ(1) 函数相加 也是n的一个线性函数，即Θ(n)

在第四章 用主定理证明T(n)为Θ(nlgn)，lgn代表log2n，在最坏情况下，运行时间为 Θ(nlgn) 的归并排序 将优于运行时间为 Θ(n²) 的插入排序

直观理解 递归式的解为 T(n) = Θ(nlgn)，把递归式 重写为


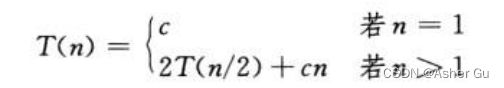
常量c 代表求解规模为1的问题 所需的时间 以及在 分解步骤 与 合并步骤 处理每个数组元素 所需的时间总代价为 cnlgn + cn（代价一直在算 分拆 和 组合（重点）消耗的时间）
顶层之下的第i层 具有2ⁱ个节点，每个节点 贡献代价 c(n/2ⁱ)，顶层之下的第i层 具有总代价 2ⁱc(n/2ⁱ) = cn，且 总层数为 lgn + 1

3.3 练习

不用哨兵，需要考虑i是否越界 且 1）j已完成 2）i是更小的那个 才能选i

MERGE(A, p, q, r)
    n = 1
    Let L[1..q - p + 1] and R[1..r - q] be new arrays
    for i = p to q
        L[n] = A[i]
        n = n + 1
    n = 1
    for j = q + 1 to r
        R[n] = A[j]
        n = n + 1
    i = 1
    j = 1
    for k = p to r
        if i ≤ q - p + 1 and (j > r - q or L[i] ≤ R[j])
            A[k] = L[i]
            i = i + 1
        else
            A[k] = R[j]
            j = j + 1