zoj 2615 Cells 栈的运用

题目链接：ZOJ - 2615

Scientists are conducting research on the behavior of a newly discovered Agamic Cellular Microbe. This special kind of microbe is capable of massively reproducing by itself in a short time. The lifetime of an ACM consists of three phases:
1. The infancy phase, which starts from its birth and lasts for approximately several seconds;
2. The multiplication phase, in which one ACM can procreate up to 100 offspring in only several milliseconds;
3. The mature phase, in which it remains inactive for the rest of its life.

At the beginning of the experiment, a newborn, single cell of ACM, is put into a suitable circumstance for its production. This cell, numbered as 0, starts to multiply and its descendants are numbered, starting from 1, according to their positions in the family hierarchy. During the experiment special equipment is used to record the numbers of the offspring generated by each of the ACM's. The experiment is stopped after a certain time period.

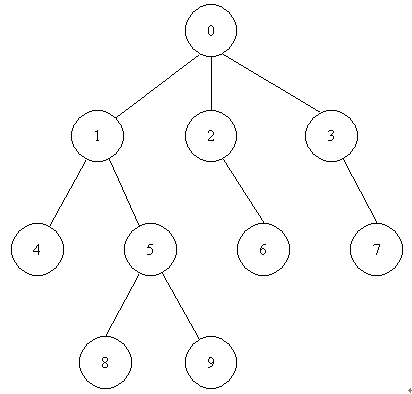
Your task is to help the scientists to determine whether one ACM is an ancestor of another.

Input Description

Standard input will contain multiple test cases. The first line of the input is a single integer T (1 <= T <= 10) which is the number of test cases. T test cases follow, each preceded by a single blank line.

Each test case starts with a single integer N (1 <= N <= 300,000) which is the number of ACM's that have their descendants recorded. The following N integers (not necessarily on a same line), Ci (0 <= i < N, 0 <= Ci <= 100), give the number of offspring of the i-th ACM. The next line contains an integer M (1 <= M <= 1,000,000) which is the number of queries. M lines follow, each contains two integers a and b, querying whether the a-th ACM is an ancestor of the b-th ACM.

The total number of ACM's may be greater than N, but would never exceed 20,000,000.

Output Description

Results should be directed to standard output. Start each case with "Case #:" on a single line, where # is the case number starting from 1. Two consecutive cases should be separated by a single blank line. No blank line should be produced after the last test case.

For each query, print either "Yes" or "No" on a single line, which is the answer to the query.

题意描述：给出一棵树，然后M个询问，每个询问u,v，判断u是否是v的祖先。

算法分析：刚开始看到这道题的时候，立马想到了LCA，于是快速找到LCA的模板并敲上，检查一下，交之，Segmentation Fault （哇，这是ZOJ独有的Judge结果），后来又改了改，交之，MLE，无语中。。。看到别人的想法是运用栈和dfs来处理即可了，给每个节点搞两个时间戳：第一次访问的时间戳和第二次访问（可以想象dfs中回溯的思想）的时间戳，然后通过时间戳来判断是否为祖先。效率上挺快的，又学习了一课。

 1 #include<iostream>

 2 #include<cstdio>

 3 #include<cstring>

 4 #include<cstdlib>

 5 #include<cmath>

 6 #include<algorithm>

 7 #include<stack>

 8 #define inf 0x7fffffff

 9 using namespace std;

10 const int maxn=300000+10;

11 const int M = 20000000+100;

12 

13 int n,m,pre[M],bac[M],vis[M],dfs_clock;

14 int an[maxn],c[maxn],sum;

15 stack<int> S;

16 

17 void dfs()

18 {

19     memset(vis,0,sizeof(vis));

20     while (!S.empty()) S.pop();

21     S.push(0);

22     while (!S.empty())

23     {

24         int u=S.top() ;

25         if (vis[u]==0)

26         {

27             vis[u]=1;

28             pre[u]= ++dfs_clock;

29             for (int i=an[u]+1 ;i<=an[u]+c[u] ;i++)

30             {

31                 if (i<n) S.push(i);

32                 else {

33                     pre[i]= ++dfs_clock;

34                     bac[i]= ++dfs_clock;

35                 }

36             }

37         }

38         else if (vis[u]==1)

39         {

40             bac[u]= ++dfs_clock;

41             S.pop();

42         }

43     }

44 }

45 

46 int main()

47 {

48     int t,ncase=1;

49     int ok=0;

50     scanf("%d",&t);

51     while (t--)

52     {

53         if (ok) printf("\n");ok=1;

54         printf("Case %d:\n",ncase++);

55         memset(pre,0,sizeof(pre));

56         memset(bac,0,sizeof(bac));

57         memset(an,0,sizeof(an));

58         memset(c,0,sizeof(c));

59         sum=0;

60         dfs_clock=0;

61         int a,b;

62         scanf("%d",&n);

63         for (int i=0 ;i<n ;i++)

64         {

65             scanf("%d",&c[i]);

66             an[i]=sum;

67             sum += c[i];

68         }

69         dfs();

70         scanf("%d",&m);

71         while (m--)

72         {

73             scanf("%d%d",&a,&b);

74             if (pre[a]<pre[b] && bac[a]>bac[b]) printf("Yes\n");

75             else printf("No\n");

76         }

77     }

78     return 0;

79 }