实验1:程序设计基础实验
实验1:程序设计基础实验
1.1 基础训练
1.数列{xn}的定义是x1 = 0, x2 = 1, xn= xn-1 + 2xn-2(n=3,4···)
用循环语句编程给出该数列的前40项(要求将结果用行向量x存储)。
代码:
clear;
clc;
x = zeros(1,40); %产生一个含有40个0的行向量赋值给x
x(1) = 0;
x(2) = 1; %对前两项赋值
for i = 3:40
x(i)=x(i-1)+2*x(i-2);
end %利用循环结构进行其余项赋值
disp(x); %输出x
2. 算法设计, 循环语句与枚举法
请找出1到1000中满足a2-100b=a的正整数 a,b(1<=a<=1000,1<=b<=1000).编写函数依次返回行向量a,b(其中a(i),b(i)为第i组解),其中数组a中元素是递增排序.请先写出求解算法,再给出程序.
解:
算法:
开始
初始化 x 范围为 1 到 1000 的数组
初始化 y 为和 x 相同的数组
创建一个二维网格 X 和 Y,其中 X 和 Y 分别为 x 和 y 的扩展矩阵
根据条件 X^2 - 100*Y == X,在网格中找到符合条件的索引
将符合条件的值赋给变量 a 和 b
返回变量 a 和 b
结束
代码:
function [a, b] = experiment2_fun() %定义函数
x = [1:1000]; %创建初始数组
y = x;
[X, Y] = meshgrid(x, y); %形成2d网络
idx = X.^2 - 100*Y == X;
a = X(idx);
b = Y(idx); %找到符合条件的值并赋值给a,b
end
3. 根据股票交易数据绘图
已知文件SH600004.mat包含了一个矩阵M.通过程序“load SH600004.mat”可以导入该文件存储的矩阵M.矩阵M存储了一只股票的交易数据.矩阵M的每行存储了一天的交易数据.以第i行为例说明矩阵M各列的含义如下:
M(i,1)日期,整数如20210301表示矩阵M本行数据为2021年3月1日的交易数据.
M(i,2) 开盘价,单位: 元
M(i,3) 最高价,单位: 元
M(i,4) 最低价,单位: 元
M(i,5) 收盘价,单位: 元
M(i,6) 成交额,单位: 元
M(i,7) 成交量,单位: 股
请完成下列任务:
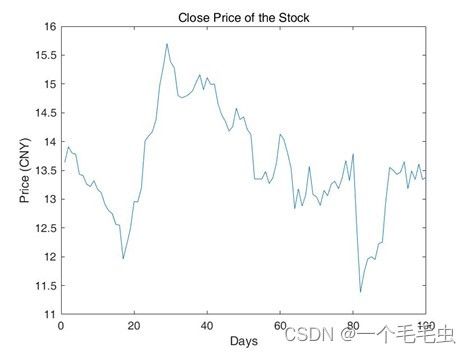
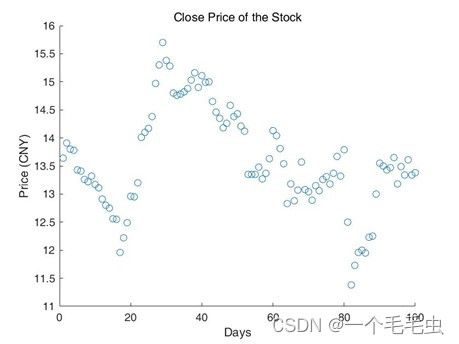
(1) 绘制出该只股票最近100个交易日内的收盘价曲线和散点图.(绘图时可将横坐标数据取为自然数)
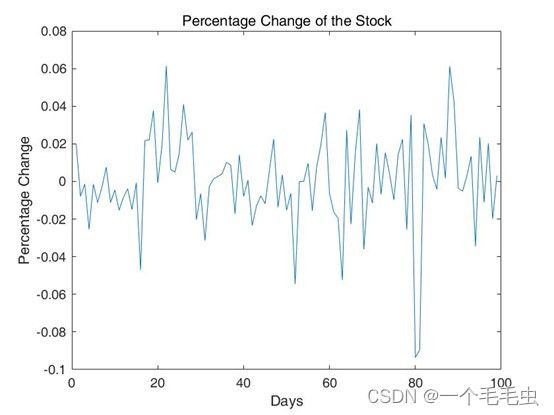
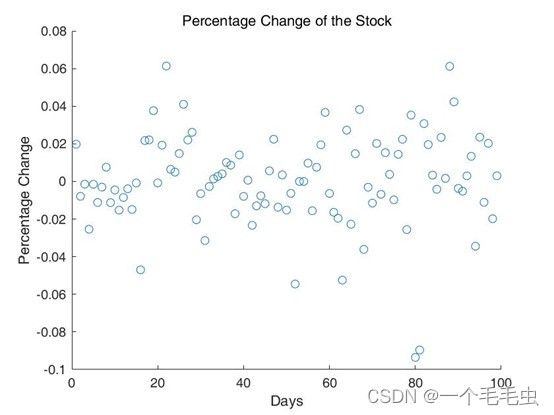
(2) 绘制出该只股票最近100个交易日的涨幅变化曲线和散点图.“涨幅”通过当日收盘价相对于前一个交易日的“收盘价”来计算.另外再用bar绘制涨幅的柱状图.
代码:
% 导入数据
load('SH600004.mat');
% 取最近100个交易日的数据
recent_data = M(end-99:end, :);
% 获取收盘价数据
close_prices = recent_data(:, 5);
% 绘制收盘价曲线
figure;
plot(close_prices);
xlabel('Days');
ylabel('Price (CNY)');
title('Close Price of the Stock');
% 绘制收盘价散点图
figure;
scatter(1:100, close_prices);
xlabel('Days');
ylabel('Price (CNY)');
title('Close Price of the Stock');
% 计算涨幅
price_diff = diff(close_prices);
percentage_change = price_diff ./ close_prices(1:end-1);
% 绘制涨幅变化曲线
figure;
plot(percentage_change);
xlabel('Days');
ylabel('Percentage Change');
title('Percentage Change of the Stock');
% 绘制涨幅散点图
figure;
scatter(1:99, percentage_change);
xlabel('Days');
ylabel('Percentage Change');
title('Percentage Change of the Stock');
% 绘制涨幅的柱状图
figure;
bar(1:99, percentage_change);
xlabel('Days');
ylabel('Percentage Change');
title('Percentage Change of the Stock');
1.2 综合训练
一.实验问题
背景:用长度为1200厘米的条材,分别截成长度为64厘米与85厘米的两种成品。
请用穷举法找出一根条材的所有切割方式,并给出每种切割方式的具体信息(包括余料长度)。说明:一根条材最多截出18根64厘米的成品,或14根85厘米的成品。
二. 实验目的
认识穷举法及其实现方式。熟悉for语句在穷举法中的应用。
三.实验过程
代码:
% 设置切割长度
length1 = 64; % 第一种成品长度
length2 = 85; % 第二种成品长度
% 初始化切割方式和余料长度
cutting_patterns = [];
remnants = [];
% 循环遍历所有可能的切割数量
for num1 = 0:18 % 第一种成品数量从0到18
for num2 = 0:14 % 第二种成品数量从0到14
% 计算总长度和余料长度
total_length = num1 * length1 + num2 * length2;
remnant = 1200 - total_length;
% 判断余料长度是否满足要求
if remnant > 0 && remnant < length1
% 保存切割方式和余料长度
cutting_patterns = [cutting_patterns; num1, num2];
remnants = [remnants; remnant];
end
end
end
% 显示所有切割方式和余料长度
disp('切割方式 第一种成品数量 第二种成品数量 余料长度');
for i = 1:size(cutting_patterns, 1)
pattern = cutting_patterns(i, :);
remnant = remnants(i);
fprintf('%3d %14d %14d %12d\n', i, pattern(1), pattern(2), remnant);
end
运行结果:
四. 实验自评与改进方向
**实验自评:**通过本次实验,我基本完成了实验要求,取得了预期的效果。在第2题中,考虑到采用for循环遍历算法耗费时间较长,并不是最优解,所以改用meshgrid函数创建网格网络来优化算法。
**改进方向:**还应当进一步熟悉MATLAB相关语法,利用MATLAB矩阵运算的优势优化算法。
五. 实验体会,收获及建议
通过完成实验项目,我对数学实验的基本方法有了进一步的理解与掌握,同时巩固了MATLAB基础语法知识。尤其是掌握了用MATLAB绘制图形的方法,为研究其他问题提供了极大的便利。