编译原理(三)词法分析
词法分析
词法分析是编译的第一个阶段,它的主要任务是从左到右逐个字符地对源程序进行扫描,产生一个个单词序列。
词法分析阶段设计的主要问题是字符串(单词)的识别问题。具体说,如何判定任意的一个字符串是否为合法字符串(单词)的问题。
字符串(单词)集合可用不同的工具来表示,常见的有:
- 单词的描述技术:正规式。
- 识别机制:有穷自动机(有限自动机)。
因此,要研究如何从正规表达式或自动机构造出相应的单词识别器的问题。这种识别器在编译器中称为词法分析器。
一、有穷自动机
有穷自动机(也称有限自动机)作为一种识别装置,它能准确地识别正规集,即识别正规文法所定义的语言和正规式所表示的集合。
引入有穷自动机这个理论,正是为词法分析程序的自动构造寻找特殊的方法和工具。
1. 确定的有穷自动机(Deterministic Finite Automata)
DFA定义:
一个确定的有穷自动机(DFA)M是一个五元组:M=(Q,Σ,δ,S,Z)其中
- Q是一个有穷集,它的每个元素称为一个状态;
- Σ是一个有穷字母表,它的每个元素称为一个输入符号;
- δ是转换函数,是在Q×Σ→Q上的单值映射,如 δ (p,a)=q,(p∈Q, q∈Q)意味着,当前状态为P,输入符为a时,将转换为下一个状态Q,我们把q称作p的一个后继状态;
- S∈Q是唯一的一个初态;
- Z ≤ Q是一个终态集,终态也称可接受状态或结束状态。
对定义的解释:
- 所谓自动机不是一台实际的机器,而是一种数学模型,来模拟计算机的识别功能。
- 所谓确定性是指δ (p,a)→q,q是唯一的。
- 用上述定义中的5条来识别一个序列是否可被机器接收。
接收→ 格式正确
DFA 的例子:
DFA M=({S,U,V,Q},{a,b},δ,S,{Q})其中δ定义为:
δ (S,a)=U δ (V,a)=U
δ (S,b)=V δ (V,b)=Q
δ (U,a)=Q δ (Q,a)=Q
δ (U,b)=V δ (Q,b)=Q
DFA的表示方法1(状态转换图)
一个DFA可以表示成一个状态图(或称状态转换图)。假定DFA M含有m个状态,n个输入字符,那么这个状态图含有m个结点,每个结点最多有n个弧射出,每条弧用Σ中的一个不同输入字符作标记。
整个图含有唯一一个初态结点和若干个终态结点,初态结点冠以双箭头“=>”,终态结点用双圈表示,若 δ (p,a)=q,则从状态结点p到状态结点q画标记为a的弧;
一个DFA还可以用一个矩阵表示,该矩阵的行表示状态,列表示输入字符,矩阵元素表示相应状态行和输入字符列下的新状态,即p行a列为δ (p,a)的值。用双箭头“=>”标明初态;否则第一行即是初态,相应终态行在表的右端标以1,非终态标以0。
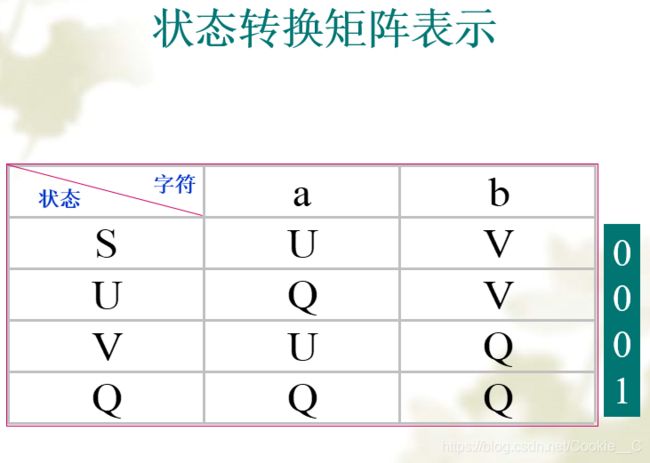
DFA的识别功能:
对于∑*中的任何字符串t,若存在一条从初态结到某一终态结的道路,且这条路上所有弧的标记符连接成的字符串等于t,则称t为DFA M所接受(识别)。
若M的初态结同时又是终态结,则ε可被识别。
DFA的等价:
DFA M所能接受的符号串的全体记为L(M)。对于任何两个有穷自动机M和M′,如果L(M)=L(M′),则称M与M′是等价的。
确定性
DFA的确定性表现在转换函数δ:Q×Σ→Q是一个单值函数,也就是说,对任何状态P∈K,和输入符号a∈Σ,δ (p,a)唯一地确定了下一个状态。
从状态转换图来看,若字母表Σ含有n个输入字符,那末任何一个状态结点最多有n条弧射出,而且每条弧以一个不同的输入字符标记。
2. 不确定的有穷自动机(Nondeterministic Finite Automata)
NFA M={Q,Σ,δ ,S,Z},其中
- Q为状态的有穷非空集, (与DFA相同)
- Σ 为有穷输入字母表,(与DFA相同)
- 映射δ为Qx Σ → Q的多值映射,
- S∈Q是唯一的一个初态,(与DFA相同)
- Z ≤ Q为终止状态集。 (与DFA相同)
NFA的表示方法1(状态转换图)
一个含有m个状态和n个输入字符的NFA可表示成一个状态转换图:这张图含有m个状态结,每个结可射出若干条箭弧与别的结相连接,每条弧用Σ中的一个字符作标记,整个图含有一个初态结和若干个终态结。
NFA的识别功能:
对于Σ﹡中的任何一个串t,若存在一条从某一初态结到某一终态结的道路,且这条道路上所有弧的标记字依序连接成的串等于t,则称t可为NFA M所识别(读出或接受)。
NFA M所能接受的符号串的全体记为L(M)。
3.具有ε动作的FA
前面在定义NFA和DFA时,对映射的限制是仅当FA扫视Σ中的一个字符时,才发生状态的转移。
如果弧上允许标记ε,即允许FA对ε也作状态的转移,则称此自动机为ε自动机,记为ε NFA或εDFA。
FA中映射δ的扩充:
映射δ为Qx Σ* 到Q的子集。
每个弧线用Σ*中的一个字作标记(字符串)
对于Σ﹡中的任何一个串t,若存在一条从初态结到某一终态结的道路,且这条道路上所有弧的标记字依序连接成的串(不理睬那些标记为ε的弧)等于t,则称t可为NFA M所识别(读出或接受)。
若M的某些结既是初态结又是终态结,或者存在一条从某个初态结到某个终态结的道路,其上所有弧的标记均为ε,那么空字可为M所接受。
4.NFA到DFA的变换
在NFA中,由于某些状态的转移须从若干个可能的后续状态中进行选择,故一个NFA对符号串的识别必然是一个试探的过程。
这种不确定性给识别过程带来的反复,无疑会影响到FA的工作效率。
子集法——将具有ε动作的NFA转换成接受同样语言的DFA。
NFA的确定化(子集法)
所谓确定化是指NFA →DFA的等价转化,用子集法来进行确定化。
为此,首先定义一个状态集合 I 的ε—闭包的概念。
- 状态集合I的ε-闭包
表示为ε-closure(I),其中I是NFA的状态集的一个子集。
①若s ∈ I ,则s∈ε-closure(I)。
状态集合I的任何状态s都属于ε-closure(I)。
②若s ∈ I ,那么从s出发经任意条ε弧而能到达的任何状态都属于ε-closure(I) 。 - 状态集合I的a弧转换,表示为move(I,a)定义为状态集合J,即J =move(I,a)。
其中J是所有那些可从I中的某一状态经过一条a弧而到达的状态的全体。
Ia= ε-closure(J)

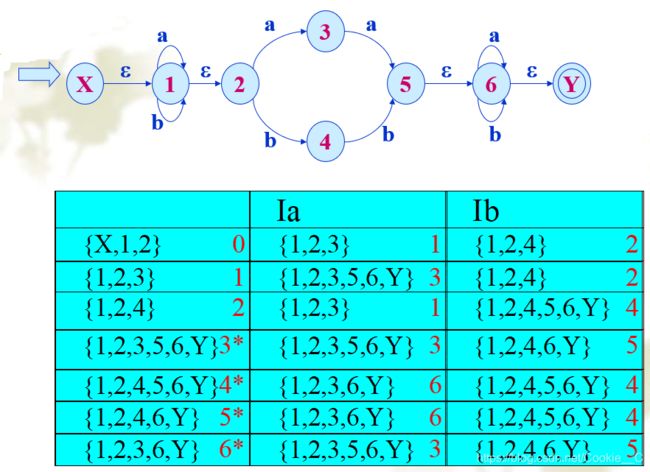
NFA确定化的步骤:
设∑={a,b},则NFA的确定化步骤如下:
1、造一张表,包含三列,第一列为I,余下的两列为Ia,Ib。
2、置首行首列为ε_closure{X}。
3、若某行首列对应子集已确定,则计算Ia,以及Ib;新出现状态子集加入下行首列。
4、重复3,直至状态子集收敛。
5、状态子集重新命名。
二、正规集、正规文法和正规式
正规式
正规式也称正则表达式,正规表达式(regular expression)是说明单词的模式的一种重要的表示法(记号),是定义正规集的数学工具。我们用以描述单词符号。 程序设计语言的单词都能用正规式来定义。
下面是正规式和它所表示的正规集的递归定义:
- 正规式中的符号:
**