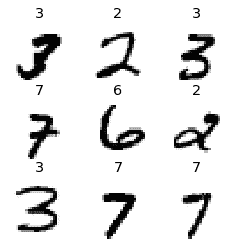绝不原创的飞龙

FastAI 之书（面向程序员的 FastAI）（六）

原文：www.bookstack.cn/read/th-fastai-book

译者：飞龙

协议：CC BY-NC-SA 4.0

第十三章：卷积神经网络

原文：www.bookstack.cn/read/th-fastai-book/44d8848dfac0c1b0.md

译者：飞龙

协议：CC BY-NC-SA 4.0

在第四章中，我们学习了如何创建一个识别图像的神经网络。我们能够在区分 3 和 7 方面达到 98%以上的准确率，但我们也看到 fastai 内置的类能够接近 100%。让我们开始尝试缩小这个差距。

在本章中，我们将首先深入研究卷积是什么，并从头开始构建一个 CNN。然后，我们将研究一系列技术来改善训练稳定性，并学习库通常为我们应用的所有调整，以获得出色的结果。

卷积的魔力

机器学习从业者手中最强大的工具之一是特征工程。特征是数据的一种转换，旨在使其更容易建模。例如，我们在第九章中用于我们表格数据集预处理的add_datepart函数向 Bulldozers 数据集添加了日期特征。我们能够从图像中创建哪些特征呢？

术语：特征工程

创建输入数据的新转换，以使其更容易建模。

在图像的背景下，特征是一种视觉上独特的属性。例如，数字 7 的特征是在数字的顶部附近有一个水平边缘，以及在其下方有一个从右上到左下的对角边缘。另一方面，数字 3 的特征是在数字的左上角和右下角有一个方向的对角边缘，在左下角和右上角有相反的对角边缘，在中间、顶部和底部有水平边缘等等。那么，如果我们能够提取关于每个图像中边缘出现位置的信息，然后将该信息用作我们的特征，而不是原始像素呢？

事实证明，在图像中找到边缘是计算机视觉中非常常见的任务，而且非常简单。为了做到这一点，我们使用一种称为卷积的东西。卷积只需要乘法和加法——这两种操作是我们将在本书中看到的每个深度学习模型中绝大部分工作的原因！

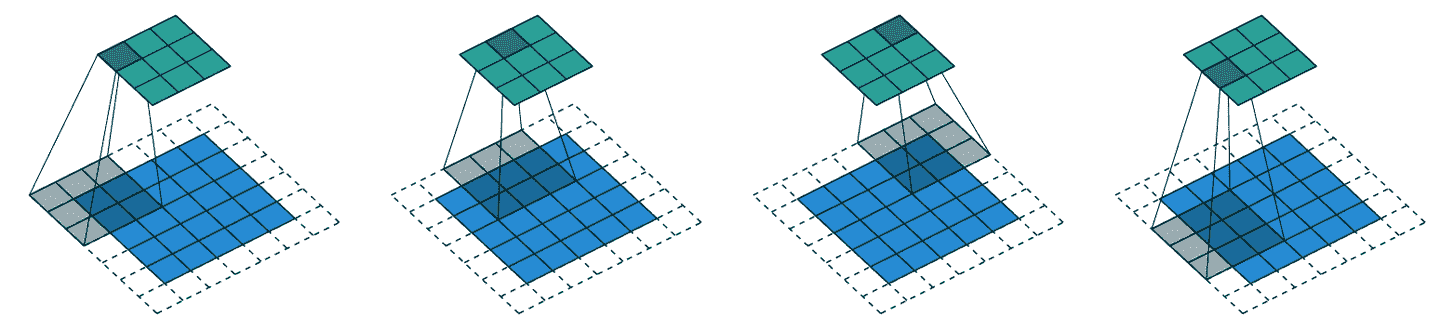
卷积将一个卷积核应用于图像。卷积核是一个小矩阵，例如图 13-1 右上角的 3×3 矩阵。

应用卷积到一个位置

图 13-1。将卷积应用到一个位置

左侧的 7×7 网格是我们将应用卷积核的图像。卷积操作将卷积核的每个元素与图像的一个 3×3 块的每个元素相乘。然后将这些乘积的结果相加。图 13-1 中的图示显示了将卷积核应用于图像中单个位置的示例，即围绕 18 单元格的 3×3 块。

让我们用代码来做这个。首先，我们创建一个小的 3×3 矩阵如下：

top_edge = tensor([[-1,-1,-1],
                   [ 0, 0, 0],
                   [ 1, 1, 1]]).float()

我们将称之为卷积核（因为这是时髦的计算机视觉研究人员称呼的）。当然，我们还需要一张图片：

path = untar_data(URLs.MNIST_SAMPLE)

im3 = Image.open(path/'train'/'3'/'12.png')
show_image(im3);

现在我们将取图像的顶部 3×3 像素正方形，并将这些值中的每一个与我们的卷积核中的每个项目相乘。然后我们将它们加在一起，就像这样：

im3_t = tensor(im3)
im3_t[0:3,0:3] * top_edge

tensor([[-0., -0., -0.],
        [0., 0., 0.],
        [0., 0., 0.]])

(im3_t[0:3,0:3] * top_edge).sum()

tensor(0.)

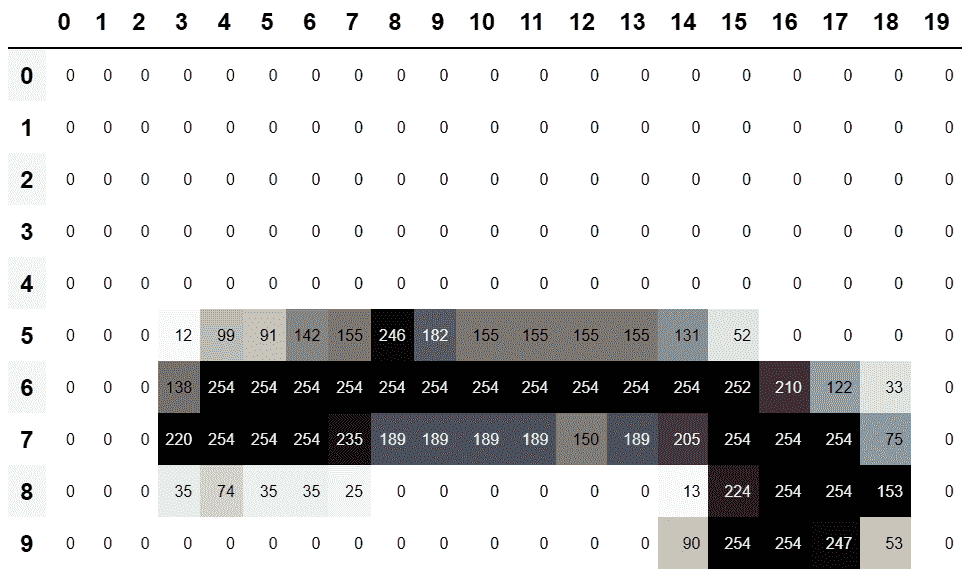
到目前为止并不是很有趣——左上角的所有像素都是白色的。但让我们选择一些更有趣的地方：

df = pd.DataFrame(im3_t[:10,:20])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')

在 5,7 单元格处有一个顶边。让我们在那里重复我们的计算：

(im3_t[4:7,6:9] * top_edge).sum()

tensor(762.)

在 8,18 单元格处有一个右边缘。这给我们带来了什么？

(im3_t[7:10,17:20] * top_edge).sum()

tensor(-29.)

正如您所看到的，这个小计算返回了一个高数字，其中 3×3 像素的正方形代表顶边（即，在正方形顶部有低值，紧接着是高值）。这是因为我们的卷积核中的-1值在这种情况下影响很小，但1值影响很大。

让我们稍微看一下数学。过滤器将在我们的图像中取任意大小为 3×3 的窗口，如果我们像这样命名像素值

a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9

它将返回a 1 + a 2 + a 3 - a 7 - a 8 - a 9。如果我们在图像的某个部分，其中a 1，a 2和a 3加起来等于a 7，a 8和a 9，那么这些项将互相抵消，我们将得到 0。然而，如果a 1大于a 7，a 2大于a 8，a 3大于a 9，我们将得到一个更大的数字作为结果。因此，这个过滤器检测水平边缘，更准确地说，我们从图像顶部的亮部到底部的暗部。

将我们的过滤器更改为顶部为1，底部为-1的行将检测从暗到亮的水平边缘。将1和-1放在列而不是行中会给我们检测垂直边缘的过滤器。每组权重将产生不同类型的结果。

让我们创建一个函数来为一个位置执行此操作，并检查它是否与之前的结果匹配：

def apply_kernel(row, col, kernel):
    return (im3_t[row-1:row+2,col-1:col+2] * kernel).sum()

apply_kernel(5,7,top_edge)

tensor(762.)

但请注意，我们不能将其应用于角落（例如，位置 0,0），因为那里没有完整的 3×3 正方形。

映射卷积核

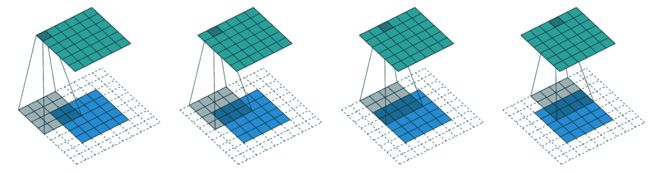
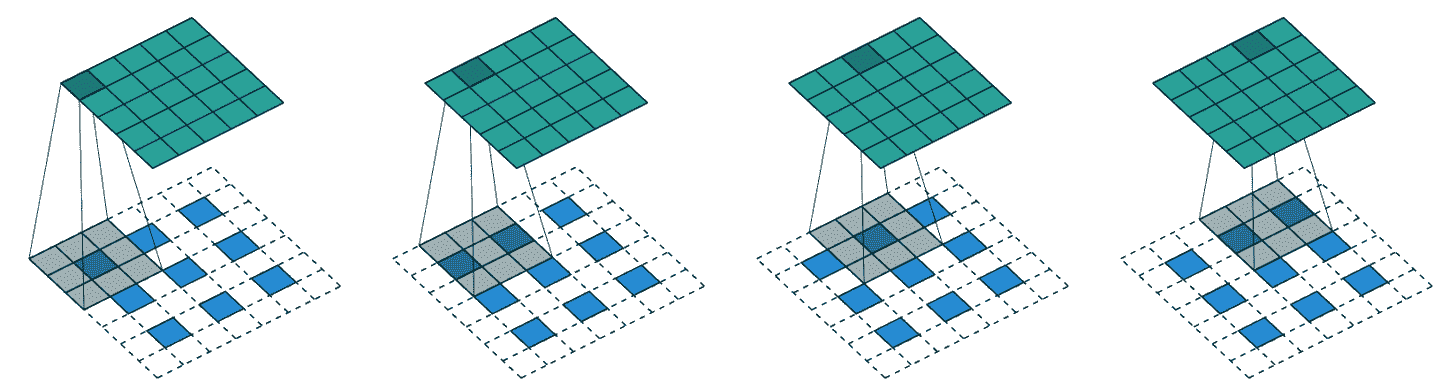
我们可以在坐标网格上映射apply_kernel()。也就是说，我们将取我们的 3×3 卷积核，并将其应用于图像的每个 3×3 部分。例如，图 13-2 显示了 3×3 卷积核可以应用于 5×5 图像第一行的位置。

图 13-2. 在网格上应用卷积核

要获得坐标网格，我们可以使用嵌套列表推导，如下所示：

[[(i,j) for j in range(1,5)] for i in range(1,5)]

[[(1, 1), (1, 2), (1, 3), (1, 4)],
 [(2, 1), (2, 2), (2, 3), (2, 4)],
 [(3, 1), (3, 2), (3, 3), (3, 4)],
 [(4, 1), (4, 2), (4, 3), (4, 4)]]

嵌套列表推导

在 Python 中经常使用嵌套列表推导，所以如果你以前没有见过它们，请花几分钟确保你理解这里发生了什么，并尝试编写自己的嵌套列表推导。

这是将我们的卷积核应用于坐标网格的结果：

rng = range(1,27)
top_edge3 = tensor([[apply_kernel(i,j,top_edge) for j in rng] for i in rng])

show_image(top_edge3);

看起来不错！我们的顶部边缘是黑色的，底部边缘是白色的（因为它们是顶部边缘的相反）。现在我们的图像中也包含负数，matplotlib已自动更改了我们的颜色，使得白色是图像中最小的数字，黑色是最高的，零显示为灰色。

我们也可以尝试同样的方法来处理左边缘：

left_edge = tensor([[-1,1,0],
                    [-1,1,0],
                    [-1,1,0]]).float()

left_edge3 = tensor([[apply_kernel(i,j,left_edge) for j in rng] for i in rng])

show_image(left_edge3);

正如我们之前提到的，卷积是将这样的内核应用于网格的操作。Vincent Dumoulin 和 Francesco Visin 的论文“深度学习卷积算术指南”中有许多出色的图表，展示了如何应用图像内核。图 13-3 是论文中的一个示例，显示了（底部）一个浅蓝色的 4×4 图像，应用了一个深蓝色的 3×3 内核，创建了一个顶部的 2×2 绿色输出激活图。

图 13-3。将 3×3 内核应用于 4×4 图像的结果（由 Vincent Dumoulin 和 Francesco Visin 提供）

看一下结果的形状。如果原始图像的高度为h，宽度为w，我们可以找到多少个 3×3 窗口？正如您从示例中看到的，有h-2乘以w-2个窗口，因此我们得到的结果图像的高度为h-2，宽度为w-2。

我们不会从头开始实现这个卷积函数，而是使用 PyTorch 的实现（它比我们在 Python 中能做的任何事情都要快）。

PyTorch 中的卷积

卷积是一个如此重要且广泛使用的操作，PyTorch 已经内置了它。它被称为F.conv2d（回想一下，F是从torch.nn.functional中导入的 fastai，正如 PyTorch 建议的）。PyTorch 文档告诉我们它包括这些参数：

input

形状为(minibatch, in_channels, iH, iW)的输入张量

weight

形状为(out_channels, in_channels, kH, kW)的滤波器

这里iH，iW是图像的高度和宽度（即28,28），kH，kW是我们内核的高度和宽度（3,3）。但显然 PyTorch 期望这两个参数都是秩为 4 的张量，而当前我们只有秩为 2 的张量（即矩阵，或具有两个轴的数组）。

这些额外轴的原因是 PyTorch 有一些技巧。第一个技巧是 PyTorch 可以同时将卷积应用于多个图像。这意味着我们可以一次在批次中的每个项目上调用它！

第二个技巧是 PyTorch 可以同时应用多个内核。因此，让我们也创建对角边缘内核，然后将我们的四个边缘内核堆叠成一个单个张量：

diag1_edge = tensor([[ 0,-1, 1],
                     [-1, 1, 0],
                     [ 1, 0, 0]]).float()
diag2_edge = tensor([[ 1,-1, 0],
                     [ 0, 1,-1],
                     [ 0, 0, 1]]).float()

edge_kernels = torch.stack([left_edge, top_edge, diag1_edge, diag2_edge])
edge_kernels.shape

torch.Size([4, 3, 3])

为了测试这个，我们需要一个DataLoader和一个样本小批量。让我们使用数据块 API：

mnist = DataBlock((ImageBlock(cls=PILImageBW), CategoryBlock),
                  get_items=get_image_files,
                  splitter=GrandparentSplitter(),
                  get_y=parent_label)

dls = mnist.dataloaders(path)
xb,yb = first(dls.valid)
xb.shape

torch.Size([64, 1, 28, 28])

默认情况下，fastai 在使用数据块时会将数据放在 GPU 上。让我们将其移动到 CPU 用于我们的示例：

xb,yb = to_cpu(xb),to_cpu(yb)

一个批次包含 64 张图片，每张图片有 1 个通道，每个通道有 28×28 个像素。F.conv2d也可以处理多通道（彩色）图像。通道是图像中的单个基本颜色——对于常规全彩图像，有三个通道，红色、绿色和蓝色。PyTorch 将图像表示为一个秩为 3 的张量，具有以下维度：

[*channels*, *rows*, *columns*]

我们将在本章后面看到如何处理多个通道。传递给F.conv2d的内核需要是秩为 4 的张量：

[*channels_in*, *features_out*, *rows*, *columns*]

edge_kernels目前缺少其中一个：我们需要告诉 PyTorch 内核中的输入通道数是 1，我们可以通过在第一个位置插入一个大小为 1 的轴来实现（这称为单位轴），PyTorch 文档显示in_channels应该是预期的。要在张量中插入一个单位轴，我们使用unsqueeze方法：

edge_kernels.shape,edge_kernels.unsqueeze(1).shape

(torch.Size([4, 3, 3]), torch.Size([4, 1, 3, 3]))

现在这是edge_kernels的正确形状。让我们将所有这些传递给conv2d：

edge_kernels = edge_kernels.unsqueeze(1)

batch_features = F.conv2d(xb, edge_kernels)
batch_features.shape

torch.Size([64, 4, 26, 26])

输出形状显示我们有 64 个图像在小批量中，4 个内核，以及 26×26 的边缘映射（我们从前面讨论中开始是 28×28 的图像，但每边丢失一个像素）。我们可以看到我们得到了与手动操作时相同的结果：

show_image(batch_features[0,0]);

PyTorch 最重要的技巧是它可以使用 GPU 并行地完成所有这些工作-将多个核应用于多个图像，跨多个通道。并行进行大量工作对于使 GPU 高效工作至关重要；如果我们一次执行每个操作，通常会慢几百倍（如果我们使用前一节中的手动卷积循环，将慢数百万倍！）。因此，要成为一名优秀的深度学习从业者，一个需要练习的技能是让 GPU 一次处理大量工作。

不要在每个轴上丢失这两个像素会很好。我们这样做的方法是添加填充，简单地在图像周围添加额外的像素。最常见的是添加零像素。

步幅和填充

通过适当的填充，我们可以确保输出激活图与原始图像的大小相同，这在构建架构时可以使事情变得简单得多。图 13-4 显示了添加填充如何允许我们在图像角落应用核。

图 13-4。带填充的卷积

使用 5×5 输入，4×4 核和 2 像素填充，我们最终得到一个 6×6 的激活图，如我们在图 13-5 中所看到的。

图 13-5。一个 4×4 的核与 5×5 的输入和 2 像素的填充（由 Vincent Dumoulin 和 Francesco Visin 提供）

如果我们添加一个大小为ks乘以ks的核（其中ks是一个奇数），为了保持相同的形状，每一侧所需的填充是ks//2。对于ks的偶数，需要在上/下和左/右两侧填充不同数量，但实际上我们几乎从不使用偶数滤波器大小。

到目前为止，当我们将核应用于网格时，我们每次将其移动一个像素。但我们可以跳得更远；例如，我们可以在每次核应用后移动两个像素，就像图 13-6 中所示。这被称为步幅-2卷积。实践中最常见的核大小是 3×3，最常见的填充是 1。正如您将看到的，步幅-2 卷积对于减小输出大小很有用，而步幅-1 卷积对于添加层而不改变输出大小也很有用。

图 13-6。一个 3×3 的核与 5×5 的输入，步幅 2 卷积和 1 像素填充（由 Vincent Dumoulin 和 Francesco Visin 提供）

在大小为h乘以w的图像中，使用填充 1 和步幅 2 将给出大小为(h+1)//2乘以(w+1)//2的结果。每个维度的一般公式是

(n + 2*pad - ks) // stride + 1

其中pad是填充，ks是我们核的大小，stride是步幅。

现在让我们看看如何计算我们卷积结果的像素值。

理解卷积方程

为了解释卷积背后的数学，fast.ai 学生 Matt Kleinsmith 提出了一个非常聪明的想法，展示了不同视角的 CNNs。事实上，这个想法非常聪明，非常有帮助，我们也会在这里展示！

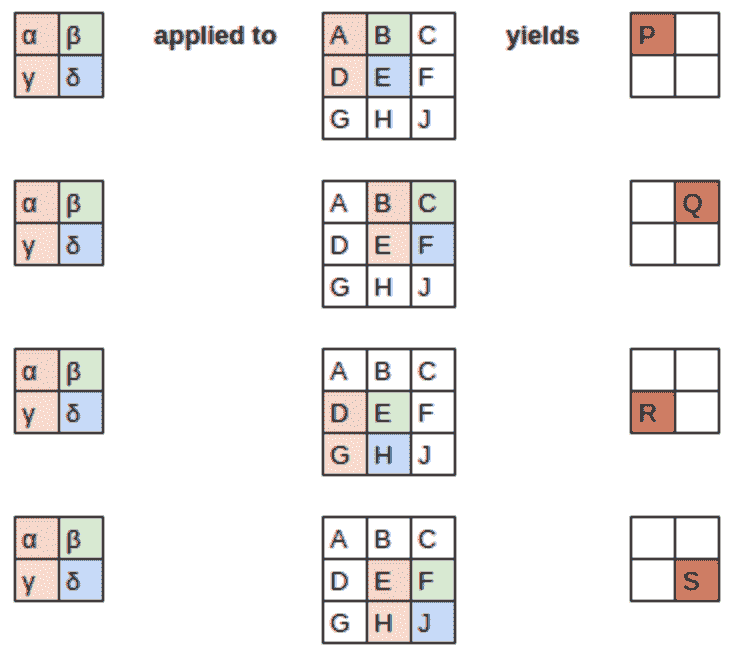
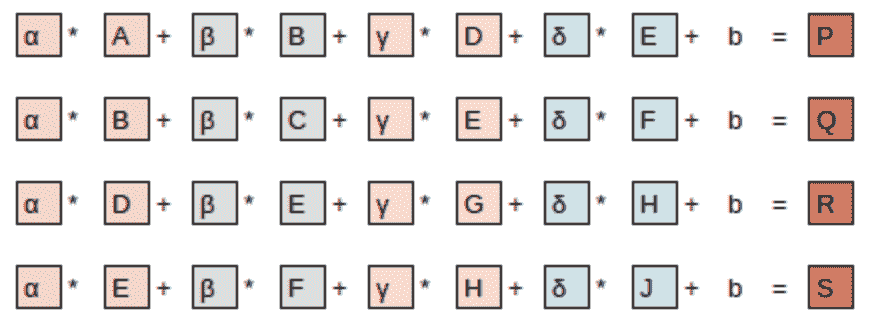
这是我们的 3×3 像素图像，每个像素都用字母标记：

这是我们的核，每个权重都用希腊字母标记：

由于滤波器适合图像四次，我们有四个结果：

图 13-7 显示了我们如何将核应用于图像的每个部分以产生每个结果。

图 13-7。应用核

方程视图在图 13-8 中。

图 13-8。方程

请注意，偏置项b对于图像的每个部分都是相同的。您可以将偏置视为滤波器的一部分，就像权重（α、β、γ、δ）是滤波器的一部分一样。

这里有一个有趣的见解——卷积可以被表示为一种特殊类型的矩阵乘法，如图 13-9 所示。权重矩阵就像传统神经网络中的那些一样。但是，这个权重矩阵具有两个特殊属性：

灰色显示的零是不可训练的。这意味着它们在优化过程中将保持为零。
一些权重是相等的，虽然它们是可训练的（即可更改的），但它们必须保持相等。这些被称为共享权重。

零对应于滤波器无法触及的像素。权重矩阵的每一行对应于滤波器的一次应用。

图 13-9。卷积作为矩阵乘法

现在我们了解了卷积是什么，让我们使用它们来构建一个神经网络。

我们的第一个卷积神经网络

没有理由相信某些特定的边缘滤波器是图像识别最有用的卷积核。此外，我们已经看到在后续层中，卷积核变成了来自较低层特征的复杂转换，但我们不知道如何手动构建这些转换。

相反，最好学习卷积核的值。我们已经知道如何做到这一点——SGD！实际上，模型将学习对分类有用的特征。当我们使用卷积而不是（或者除了）常规线性层时，我们创建了一个卷积神经网络（CNN）。

创建 CNN

让我们回到第四章中的基本神经网络。它的定义如下：

simple_net = nn.Sequential(
    nn.Linear(28*28,30),
    nn.ReLU(),
    nn.Linear(30,1)
)

我们可以查看模型的定义：

simple_net

Sequential(
  (0): Linear(in_features=784, out_features=30, bias=True)
  (1): ReLU()
  (2): Linear(in_features=30, out_features=1, bias=True)
)

现在我们想要创建一个类似于这个线性模型的架构，但是使用卷积层而不是线性层。nn.Conv2d是F.conv2d的模块等效物。在创建架构时，它比F.conv2d更方便，因为在实例化时会自动为我们创建权重矩阵。

这是一个可能的架构：

broken_cnn = sequential(
    nn.Conv2d(1,30, kernel_size=3, padding=1),
    nn.ReLU(),
    nn.Conv2d(30,1, kernel_size=3, padding=1)
)

这里需要注意的一点是，我们不需要指定28*28作为输入大小。这是因为线性层需要在权重矩阵中为每个像素设置一个权重，因此它需要知道有多少像素，但卷积会自动应用于每个像素。权重仅取决于输入和输出通道的数量以及核大小，正如我们在前一节中看到的。

想一想输出形状会是什么；然后让我们尝试一下：

broken_cnn(xb).shape

torch.Size([64, 1, 28, 28])

这不是我们可以用来进行分类的东西，因为我们需要每个图像一个单独的输出激活，而不是一个 28×28 的激活图。处理这个问题的一种方法是使用足够多的步幅为 2 的卷积，使得最终层的大小为 1。经过一次步幅为 2 的卷积后，大小将为 14×14；经过两次后，将为 7×7；然后是 4×4，2×2，最终大小为 1。

现在让我们尝试一下。首先，我们将定义一个函数，其中包含我们在每个卷积中将使用的基本参数：

def conv(ni, nf, ks=3, act=True):
    res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
    if act: res = nn.Sequential(res, nn.ReLU())
    return res

重构

重构神经网络的部分，可以减少由于架构不一致而导致的错误，也可以更明显地向读者展示哪些层的部分实际上在改变。

当我们使用步幅为 2 的卷积时，通常会同时增加特征的数量。这是因为我们通过将激活图中的激活数量减少 4 倍来减少层的容量，我们不希望一次过多地减少层的容量。

术语：通道和特征

这两个术语通常可以互换使用，指的是权重矩阵的第二轴的大小，即卷积后每个网格单元的激活数量。特征从不用于指代输入数据，但通道可以指代输入数据(通常是颜色)或网络内部的激活。

以下是我们如何构建一个简单的 CNN：

simple_cnn = sequential(
    conv(1 ,4),            #14x14
    conv(4 ,8),            #7x7
    conv(8 ,16),           #4x4
    conv(16,32),           #2x2
    conv(32,2, act=False), #1x1
    Flatten(),
)

Jeremy 说

我喜欢在每个卷积后添加类似这里的注释，以显示每个层后激活图的大小。这些注释假定输入大小为 28×28。

现在网络输出两个激活，这对应于我们标签中的两个可能级别：

simple_cnn(xb).shape

torch.Size([64, 2])

我们现在可以创建我们的Learner：

learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)

要查看模型中发生的情况，我们可以使用summary：

learn.summary()

Sequential (Input shape: ['64 x 1 x 28 x 28'])
================================================================
Layer (type)         Output Shape         Param #    Trainable
================================================================
Conv2d               64 x 4 x 14 x 14     40         True
________________________________________________________________
ReLU                 64 x 4 x 14 x 14     0          False
________________________________________________________________
Conv2d               64 x 8 x 7 x 7       296        True
________________________________________________________________
ReLU                 64 x 8 x 7 x 7       0          False
________________________________________________________________
Conv2d               64 x 16 x 4 x 4      1,168      True
________________________________________________________________
ReLU                 64 x 16 x 4 x 4      0          False
________________________________________________________________
Conv2d               64 x 32 x 2 x 2      4,640      True
________________________________________________________________
ReLU                 64 x 32 x 2 x 2      0          False
________________________________________________________________
Conv2d               64 x 2 x 1 x 1       578        True
________________________________________________________________
Flatten              64 x 2               0          False
________________________________________________________________

Total params: 6,722
Total trainable params: 6,722
Total non-trainable params: 0

Optimizer used: <function Adam at 0x7fbc9c258cb0>
Loss function: <function cross_entropy at 0x7fbca9ba0170>

Callbacks:
  - TrainEvalCallback
  - Recorder
  - ProgressCallback

请注意，最终的Conv2d层的输出是64x2x1x1。我们需要去除那些额外的1x1轴；这就是Flatten所做的。这基本上与 PyTorch 的squeeze方法相同，但作为一个模块。

让我们看看这是否训练！由于这是我们从头开始构建的比以前更深的网络，我们将使用更低的学习率和更多的时代：

learn.fit_one_cycle(2, 0.01)

时代	训练损失	验证损失	准确性	时间
0	0.072684	0.045110	0.990186	00:05
1	0.022580	0.030775	0.990186	00:05

成功！它越来越接近我们之前的resnet18结果，尽管还不完全达到，而且需要更多的时代，我们需要使用更低的学习率。我们还有一些技巧要学习，但我们越来越接近能够从头开始创建现代 CNN。

理解卷积算术

我们可以从总结中看到，我们有一个大小为64x1x28x28的输入。轴是批次、通道、高度、宽度。这通常表示为NCHW(其中N是批次大小)。另一方面，TensorFlow 使用NHWC轴顺序。这是第一层：

m = learn.model[0]
m

Sequential(
  (0): Conv2d(1, 4, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
  (1): ReLU()
)

因此，我们有 1 个输入通道，4 个输出通道和一个 3×3 的内核。让我们检查第一个卷积的权重：

m[0].weight.shape

torch.Size([4, 1, 3, 3])

总结显示我们有 40 个参数，4*1*3*3是 36。其他四个参数是什么？让我们看看偏差包含什么：

m[0].bias.shape

torch.Size([4])

我们现在可以利用这些信息来澄清我们在上一节中的陈述：“当我们使用步幅为 2 的卷积时，我们经常增加特征的数量，因为我们通过 4 的因子减少了激活图中的激活数量；我们不希望一次性太多地减少层的容量。”

每个通道都有一个偏差。(有时通道被称为特征或滤波器，当它们不是输入通道时。) 输出形状是64x4x14x14，因此这将成为下一层的输入形状。根据summary，下一层有 296 个参数。让我们忽略批次轴，保持简单。因此，对于14*14=196个位置，我们正在乘以296-8=288个权重(为简单起见忽略偏差)，因此在这一层有196*288=56,448次乘法。下一层将有7*7*(1168-16)=56,448次乘法。

这里发生的情况是，我们的步幅为 2 的卷积将网格大小从14x14减半到7x7，并且我们将滤波器数量从 8 增加到 16，导致总体计算量没有变化。如果我们在每个步幅为 2 的层中保持通道数量不变，那么网络中所做的计算量会随着深度增加而减少。但我们知道，更深层次必须计算语义丰富的特征(如眼睛或毛发)，因此我们不会期望减少计算是有意义的。

另一种思考这个问题的方式是基于感受野。

感受野

接受域是参与层计算的图像区域。在书籍网站上，您会找到一个名为conv-example.xlsx的 Excel 电子表格，展示了使用 MNIST 数字计算两个步幅为 2 的卷积层的过程。每个层都有一个单独的核。图 13-10 展示了如果我们点击conv2部分中的一个单元格，显示第二个卷积层的输出，并点击trace precedents时看到的内容。

图 13-10. Conv2 层的直接前置

这里，有绿色边框的单元格是我们点击的单元格，蓝色高亮显示的单元格是它的前置——用于计算其值的单元格。这些单元格是输入层（左侧）的对应 3×3 区域单元格和滤波器（右侧）的单元格。现在让我们再次点击trace precedents，看看用于计算这些输入的单元格。图 13-11 展示了发生了什么。

图 13-11. Conv2 层的次要前置

在这个例子中，我们只有两个步幅为 2 的卷积层，因此现在追溯到了输入图像。我们可以看到输入层中的一个 7×7 区域单元格用于计算 Conv2 层中的单个绿色单元格。这个 7×7 区域是 Conv2 中绿色激活的输入的接受域。我们还可以看到现在需要第二个滤波器核，因为我们有两个层。

从这个例子中可以看出，我们在网络中越深（特别是在一个层之前有更多步幅为 2 的卷积层时），该层中激活的接受域就越大。一个大的接受域意味着输入图像的大部分被用来计算该层中每个激活。我们现在知道，在网络的深层，我们有语义丰富的特征，对应着更大的接受域。因此，我们期望我们需要更多的权重来处理这种不断增加的复杂性。这是另一种说法，与我们在前一节提到的相同：当我们在网络中引入步幅为 2 的卷积时，我们也应该增加通道数。

在撰写这一特定章节时，我们有很多问题需要回答，以便尽可能好地向您解释 CNN。信不信由你，我们在 Twitter 上找到了大部分答案。在我们继续讨论彩色图像之前，我们将快速休息一下，与您谈谈这个问题。

关于 Twitter 的一点说明

总的来说，我们并不是社交网络的重度用户。但我们写这本书的目标是帮助您成为最优秀的深度学习从业者，我们不提及 Twitter 在我们自己的深度学习之旅中有多么重要是不合适的。

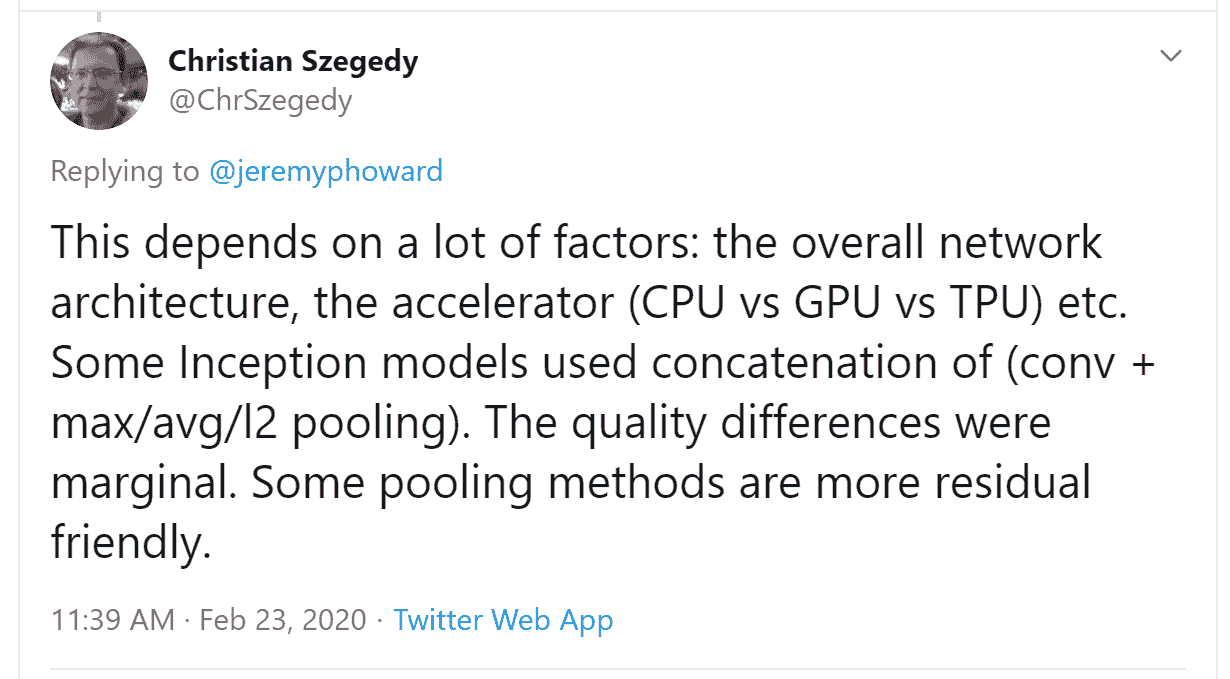
您看，Twitter 还有另一部分，远离唐纳德·特朗普和卡戴珊家族，深度学习研究人员和从业者每天都在这里交流。在我们撰写这一部分时，Jeremy 想要再次确认我们关于步幅为 2 的卷积的说法是否准确，所以他在 Twitter 上提问：

几分钟后，这个答案出现了：

Christian Szegedy 是Inception的第一作者，这是 2014 年 ImageNet 的获奖作品，也是现代神经网络中许多关键见解的来源。两小时后，这个出现了：

你认识那个名字吗？您在第二章中看到过，当时我们在谈论今天建立深度学习基础的图灵奖获得者！

Jeremy 还在 Twitter 上询问有关我们在第七章中描述的标签平滑是否准确，并再次直接从 Christian Szegedy（标签平滑最初是在 Inception 论文中引入的）那里得到了回应：

今天深度学习领域的许多顶尖人物经常在 Twitter 上活跃，并且非常乐意与更广泛的社区互动。一个好的开始方法是查看 Jeremy 的最近的 Twitter 点赞，或者Sylvain 的。这样，您可以看到我们认为有趣和有用的人发表的 Twitter 用户列表。

Twitter 是我们保持与有趣论文、软件发布和其他深度学习新闻最新的主要途径。为了与深度学习社区建立联系，我们建议在fast.ai 论坛和 Twitter 上都积极参与。

话虽如此，让我们回到本章的重点。到目前为止，我们只展示了黑白图片的示例，每个像素只有一个值。实际上，大多数彩色图像每个像素有三个值来定义它们的颜色。接下来我们将看看如何处理彩色图像。

彩色图像

彩色图片是一个三阶张量：

im = image2tensor(Image.open('images/grizzly.jpg'))
im.shape

torch.Size([3, 1000, 846])

show_image(im);

第一个轴包含红色、绿色和蓝色的通道：

_,axs = subplots(1,3)
for bear,ax,color in zip(im,axs,('Reds','Greens','Blues')):
    show_image(255-bear, ax=ax, cmap=color)

我们看到卷积操作是针对图像的一个通道上的一个滤波器（我们的示例是在一个正方形上完成的）。卷积层将接受一个具有一定数量通道的图像（对于常规 RGB 彩色图像的第一层有三个通道），并输出一个具有不同数量通道的图像。与我们的隐藏大小代表线性层中神经元数量一样，我们可以决定有多少个滤波器，并且每个滤波器都可以专门化（一些用于检测水平边缘，其他用于检测垂直边缘等等），从而产生类似我们在第二章中学习的示例。

在一个滑动窗口中，我们有一定数量的通道，我们需要同样数量的滤波器（我们不对所有通道使用相同的核）。因此，我们的核不是 3×3 的大小，而是ch_in（通道数）乘以 3×3。在每个通道上，我们将窗口的元素乘以相应滤波器的元素，然后对结果求和（如前所述），并对所有滤波器求和。在图 13-12 中给出的示例中，我们在该窗口上的卷积层的结果是红色+绿色+蓝色。

图 13-12. 在 RGB 图像上进行卷积

因此，为了将卷积应用于彩色图片，我们需要一个大小与第一个轴匹配的核张量。在每个位置，核和图像块的相应部分相乘。

然后，所有这些都相加在一起，为每个输出特征的每个网格位置产生一个单个数字，如图 13-13 所示。

图 13-13. 添加 RGB 滤波器

然后我们有ch_out这样的滤波器，因此最终，我们的卷积层的结果将是一个具有ch_out通道的图像批次，高度和宽度由前面概述的公式给出。这给我们ch_out大小为ch_in x ks x ks的张量，我们将其表示为一个四维大张量。在 PyTorch 中，这些权重的维度顺序是ch_out x ch_in x ks x ks。

此外，我们可能希望为每个滤波器设置一个偏置。在前面的示例中，我们的卷积层的最终结果将是y R + y G + y B + b。就像在线性层中一样，我们有多少个卷积核就有多少个偏置，因此偏置是大小为ch_out的向量。

在使用彩色图像进行训练 CNN 时不需要特殊机制。只需确保您的第一层有三个输入。

有很多处理彩色图像的方法。例如，您可以将它们转换为黑白色，从 RGB 转换为 HSV（色调、饱和度和值）颜色空间等。一般来说，实验证明，改变颜色的编码不会对模型结果产生任何影响，只要在转换中不丢失信息。因此，转换为黑白色是一个坏主意，因为它完全删除了颜色信息（这可能是关键的；例如，宠物品种可能具有独特的颜色）；但通常转换为 HSV 不会产生任何影响。

现在您知道了第一章中“神经网络学习到的内容”中的那些图片来自Zeiler 和 Fergus 的论文的含义！作为提醒，这是他们关于一些第 1 层权重的图片：

这是将卷积核的三个切片，对于每个输出特征，显示为图像。我们可以看到，即使神经网络的创建者从未明确创建用于查找边缘的卷积核，神经网络也会使用 SGD 自动发现这些特征。

现在让我们看看如何训练这些 CNN，并向您展示 fastai 在底层使用的所有技术，以实现高效的训练。

提高训练稳定性

由于我们在识别 3 和 7 方面做得很好，让我们转向更难的事情——识别所有 10 个数字。这意味着我们需要使用MNIST而不是MNIST_SAMPLE：

path = untar_data(URLs.MNIST)

path.ls()

(#2) [Path('testing'),Path('training')]

数据在两个名为training和testing的文件夹中，因此我们必须告诉GrandparentSplitter这一点（默认为train和valid）。我们在get_dls函数中执行此操作，该函数定义使得稍后更改批量大小变得容易：

def get_dls(bs=64):
    return DataBlock(
        blocks=(ImageBlock(cls=PILImageBW), CategoryBlock),
        get_items=get_image_files,
        splitter=GrandparentSplitter('training','testing'),
        get_y=parent_label,
        batch_tfms=Normalize()
    ).dataloaders(path, bs=bs)

dls = get_dls()

记住，在使用数据之前先查看数据总是一个好主意：

dls.show_batch(max_n=9, figsize=(4,4))

现在我们的数据准备好了，我们可以在上面训练一个简单的模型。

一个简单的基线

在本章的前面，我们基于类似于conv函数构建了一个模型：

def conv(ni, nf, ks=3, act=True):
    res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
    if act: res = nn.Sequential(res, nn.ReLU())
    return res

让我们从一个基本的 CNN 作为基线开始。我们将使用与之前相同的一个，但有一个调整：我们将使用更多的激活。由于我们有更多的数字需要区分，我们可能需要学习更多的滤波器。

正如我们讨论过的，通常我们希望每次有一个步幅为 2 的层时将滤波器数量加倍。在整个网络中增加滤波器数量的一种方法是在第一层中将激活数量加倍，然后每个之后的层也将比之前的版本大一倍。

但这会产生一个微妙的问题。考虑应用于每个像素的卷积核。默认情况下，我们使用一个 3×3 像素的卷积核。因此，在每个位置上，卷积核被应用到了总共 3×3=9 个像素。以前，我们的第一层有四个输出滤波器。因此，在每个位置上，从九个像素计算出四个值。想想如果我们将输出加倍到八个滤波器会发生什么。然后当我们应用我们的卷积核时，我们将使用九个像素来计算八个数字。这意味着它实际上并没有学到太多：输出大小几乎与输入大小相同。只有当神经网络被迫这样做时，即从操作的输出数量明显小于输入数量时，它们才会创建有用的特征。

为了解决这个问题，我们可以在第一层使用更大的卷积核。如果我们使用一个 5×5 像素的卷积核，每次卷积核应用时将使用 25 个像素。从中创建八个滤波器将意味着神经网络将不得不找到一些有用的特征：

def simple_cnn():
    return sequential(
        conv(1 ,8, ks=5),        #14x14
        conv(8 ,16),             #7x7
        conv(16,32),             #4x4
        conv(32,64),             #2x2
        conv(64,10, act=False),  #1x1
        Flatten(),
    )

正如您将在接下来看到的，我们可以在模型训练时查看模型内部，以尝试找到使其训练更好的方法。为此，我们使用ActivationStats回调，记录每个可训练层的激活的均值、标准差和直方图（正如我们所见，回调用于向训练循环添加行为；我们将在第十六章中探讨它们的工作原理）：

from fastai.callback.hook import *

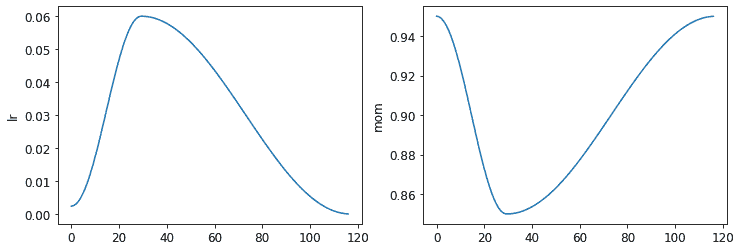
我们希望快速训练，这意味着以较高的学习率进行训练。让我们看看在 0.06 时的效果如何：

def fit(epochs=1):
    learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
                    metrics=accuracy, cbs=ActivationStats(with_hist=True))
    learn.fit(epochs, 0.06)
    return learn

learn = fit()

轮数	训练损失	验证损失	准确率	时间
0	2.307071	2.305865	0.113500	00:16

这次训练效果不佳！让我们找出原因。

传递给Learner的回调的一个方便功能是它们会自动提供，名称与回调类相同，除了使用驼峰命名法。因此，我们的ActivationStats回调可以通过activation_stats访问。我相信你还记得learn.recorder…你能猜到它是如何实现的吗？没错，它是一个名为Recorder的回调！

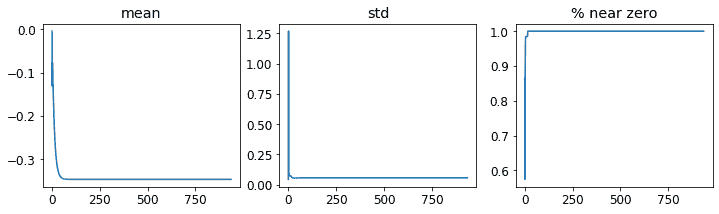
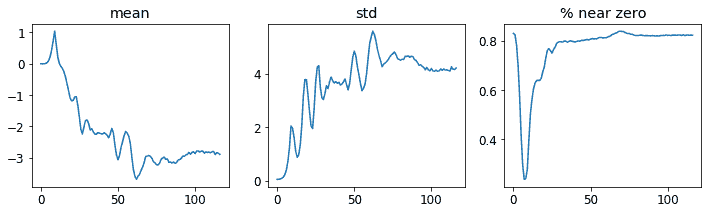
ActivationStats包含一些方便的实用程序，用于绘制训练期间的激活。plot_layer_stats(*idx*)绘制第*idx*层激活的均值和标准差，以及接近零的激活百分比。这是第一层的图表：

learn.activation_stats.plot_layer_stats(0)

通常情况下，我们的模型在训练期间应该具有一致或至少平滑的层激活均值和标准差。接近零的激活值特别有问题，因为这意味着我们的模型中有一些计算根本没有做任何事情（因为乘以零得到零）。当一个层中有一些零时，它们通常会传递到下一层…然后创建更多的零。这是我们网络的倒数第二层：

learn.activation_stats.plot_layer_stats(-2)

正如预期的那样，问题在网络末端变得更糟，因为不稳定性和零激活在层间累积。让我们看看如何使训练更稳定。

增加批量大小

使训练更稳定的一种方法是增加批量大小。较大的批次具有更准确的梯度，因为它们是从更多数据计算出来的。然而，较大的批量大小意味着每个轮数的批次更少，这意味着您的模型更新权重的机会更少。让我们看看批量大小为 512 是否有帮助：

dls = get_dls(512)

learn = fit()

轮数	训练损失	验证损失	准确率	时间
0	2.309385	2.302744	0.113500	00:08

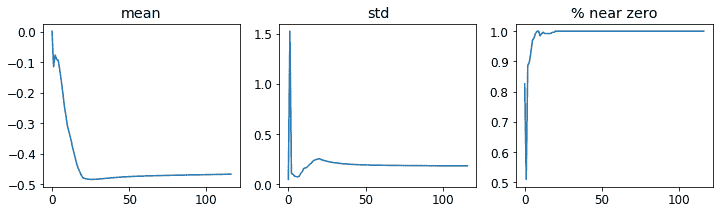
让我们看看倒数第二层是什么样的：

learn.activation_stats.plot_layer_stats(-2)

再次，我们的大多数激活值接近零。让我们看看我们可以做些什么来改善训练稳定性。

1cycle 训练

我们的初始权重不适合我们要解决的任务。因此，以高学习率开始训练是危险的：我们很可能会使训练立即发散，正如我们所见。我们可能也不想以高学习率结束训练，这样我们就不会跳过一个最小值。但我们希望在训练期间保持高学习率，因为这样我们可以更快地训练。因此，我们应该在训练过程中改变学习率，从低到高，然后再次降低到低。

莱斯利·史密斯（是的，就是发明学习率查找器的那个人！）在他的文章“超收敛：使用大学习率非常快速地训练神经网络”中发展了这个想法。他设计了一个学习率时间表，分为两个阶段：一个阶段学习率从最小值增长到最大值（预热），另一个阶段学习率再次降低到最小值（退火）。史密斯称这种方法的组合为1cycle 训练。

1cycle 训练允许我们使用比其他类型训练更高的最大学习率，这带来了两个好处：

通过使用更高的学习率进行训练，我们可以更快地训练——这种现象史密斯称之为超收敛。
通过使用更高的学习率进行训练，我们过拟合较少，因为我们跳过了尖锐的局部最小值，最终进入了更平滑（因此更具有泛化能力）的损失部分。

第二点是一个有趣而微妙的观察；它基于这样一个观察：一个泛化良好的模型，如果你稍微改变输入，它的损失不会发生很大变化。如果一个模型在较大的学习率下训练了相当长的时间，并且在这样做时能找到一个好的损失，那么它一定找到了一个泛化良好的区域，因为它在批次之间跳动很多（这基本上就是高学习率的定义）。问题在于，正如我们所讨论的，直接跳到高学习率更有可能导致损失发散，而不是看到损失改善。因此，我们不会直接跳到高学习率。相反，我们从低学习率开始，我们的损失不会发散，然后允许优化器逐渐找到参数的更平滑的区域，逐渐提高学习率。

然后，一旦我们找到了参数的一个良好平滑区域，我们希望找到该区域的最佳部分，这意味着我们必须再次降低学习率。这就是为什么 1cycle 训练有一个渐进的学习率预热和渐进的学习率冷却。许多研究人员发现，实践中这种方法导致更准确的模型和更快的训练。这就是为什么在 fastai 中fine_tune默认使用这种方法。

在第十六章中，我们将学习有关 SGD 中的动量。简而言之，动量是一种技术，优化器不仅朝着梯度的方向迈出一步，而且继续朝着以前的步骤的方向前进。 Leslie Smith 在“神经网络超参数的纪律方法：第 1 部分”中介绍了循环动量的概念。它建议动量与学习率的方向相反变化：当我们处于高学习率时，我们使用较少的动量，在退火阶段再次使用更多动量。

我们可以通过调用fit_one_cycle在 fastai 中使用 1cycle 训练：

def fit(epochs=1, lr=0.06):
    learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
                    metrics=accuracy, cbs=ActivationStats(with_hist=True))
    learn.fit_one_cycle(epochs, lr)
    return learn

learn = fit()

epoch	train_loss	valid_loss	accuracy	time
0	0.210838	0.084827	0.974300	00:08

我们终于取得了一些进展！现在它给我们一个合理的准确率。

我们可以通过在learn.recorder上调用plot_sched来查看训练过程中的学习率和动量。learn.recorder（顾名思义）记录了训练过程中发生的一切，包括损失、指标和超参数，如学习率和动量：

learn.recorder.plot_sched()

Smith 的原始 1cycle 论文使用了线性热身和线性退火。正如您所看到的，我们通过将其与另一种流行方法——余弦退火相结合，在 fastai 中改进了这种方法。fit_one_cycle提供了以下您可以调整的参数：

lr_max

将使用的最高学习率（这也可以是每个层组的学习率列表，或包含第一个和最后一个层组学习率的 Python slice对象）

div

将lr_max除以多少以获得起始学习率

div_final

将lr_max除以多少以获得结束学习率

pct_start

用于热身的批次百分比

moms

一个元组(*mom1*,*mom2*,*mom3*)，其中*mom1是初始动量，mom2是最小动量，mom3*是最终动量

让我们再次查看我们的层统计数据：

learn.activation_stats.plot_layer_stats(-2)

非零权重的百分比正在得到很大的改善，尽管仍然相当高。通过使用color_dim并传递一个层索引，我们可以更多地了解我们的训练情况：

learn.activation_stats.color_dim(-2)

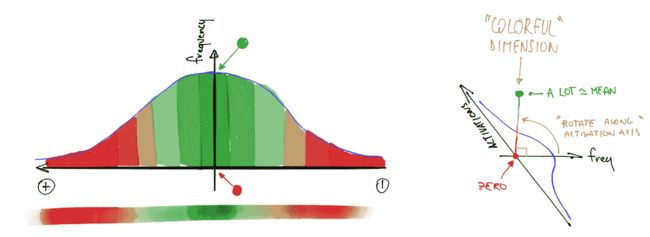
color_dim是由 fast.ai 与学生 Stefano Giomo 共同开发的。Giomo 将这个想法称为丰富多彩维度，并提供了一个深入解释这种方法背后的历史和细节。基本思想是创建一个层的激活直方图，我们希望它会遵循一个平滑的模式，如正态分布（图 13-14）。

图 13-14。丰富多彩维度的直方图（由 Stefano Giomo 提供）

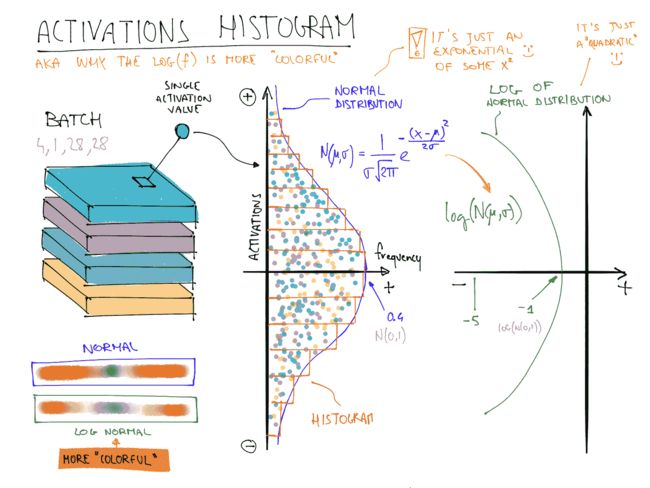
为了创建color_dim，我们将左侧显示的直方图转换为底部显示的彩色表示。然后，我们将其翻转，如右侧所示。我们发现，如果我们取直方图值的对数，分布会更清晰。然后，Giomo 描述：

每个层的最终图是通过将每批次的激活直方图沿水平轴堆叠而成的。因此，可视化中的每个垂直切片代表单个批次的激活直方图。颜色强度对应直方图的高度；换句话说，每个直方图柱中的激活数量。

图 13-15 展示了这一切是如何结合在一起的。

图 13-15。丰富多彩维度的总结（由 Stefano Giomo 提供）

这说明了为什么当f遵循正态分布时，log(f)比f更丰富多彩，因为取对数会将高斯曲线变成二次曲线，这样不会那么狭窄。

因此，让我们再次看看倒数第二层的结果：

learn.activation_stats.color_dim(-2)

这展示了一个经典的“糟糕训练”图片。我们从几乎所有激活都为零开始——这是我们在最左边看到的，所有的深蓝色。底部的明黄色代表接近零的激活。然后，在最初的几批中，我们看到非零激活数量呈指数增长。但它走得太远并崩溃了！我们看到深蓝色回来了，底部再次变成明黄色。它几乎看起来像是训练重新从头开始。然后我们看到激活再次增加并再次崩溃。重复几次后，最终我们看到激活在整个范围内分布。

如果训练一开始就能平稳进行会更好。指数增长然后崩溃的周期往往会导致大量接近零的激活，从而导致训练缓慢且最终结果不佳。解决这个问题的一种方法是使用批量归一化。

批量归一化

为了解决前一节中出现的训练缓慢和最终结果不佳的问题，我们需要解决初始大比例接近零的激活，并尝试在整个训练过程中保持良好的激活分布。

Sergey Ioffe 和 Christian Szegedy 在 2015 年的论文“Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”中提出了这个问题的解决方案。在摘要中，他们描述了我们所见过的问题：

训练深度神经网络的复杂性在于每一层输入的分布在训练过程中会发生变化，因为前一层的参数发生变化。这需要降低学习率和谨慎的参数初始化，从而减慢训练速度…我们将这种现象称为内部协变量转移，并通过对层输入进行归一化来解决这个问题。

他们说他们的解决方案如下：

将归一化作为模型架构的一部分，并对每个训练小批量进行归一化。批量归一化使我们能够使用更高的学习率，并且对初始化要求不那么严格。

这篇论文一经发布就引起了极大的兴奋，因为它包含了图 13-16 中的图表，清楚地表明批量归一化可以训练出比当前最先进技术（Inception架构）更准确且速度快约 5 倍的模型。

图 13-16. 批量归一化的影响（由 Sergey Ioffe 和 Christian Szegedy 提供）

批量归一化（通常称为batchnorm）通过取层激活的均值和标准差的平均值来归一化激活。然而，这可能会导致问题，因为网络可能希望某些激活非常高才能进行准确的预测。因此，他们还添加了两个可学习参数（意味着它们将在 SGD 步骤中更新），通常称为gamma和beta。在将激活归一化以获得一些新的激活向量y之后，批量归一化层返回gamma*y + beta。

这就是为什么我们的激活可以具有任何均值或方差，独立于前一层结果的均值和标准差。这些统计数据是分开学习的，使得我们的模型训练更容易。在训练和验证期间的行为是不同的：在训练期间，我们使用批次的均值和标准差来归一化数据，而在验证期间，我们使用训练期间计算的统计数据的运行均值。

让我们在conv中添加一个批量归一化层：

def conv(ni, nf, ks=3, act=True):
    layers = [nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)]
    layers.append(nn.BatchNorm2d(nf))
    if act: layers.append(nn.ReLU())
    return nn.Sequential(*layers)

并适应我们的模型：

learn = fit()

epoch	train_loss	valid_loss	accuracy	time
0	0.130036	0.055021	0.986400	00:10

这是一个很好的结果！让我们看看color_dim：

learn.activation_stats.color_dim(-4)

这正是我们希望看到的：激活的平稳发展，没有“崩溃”。Batchnorm 在这里真的兑现了承诺！事实上，批量归一化非常成功，我们几乎可以在所有现代神经网络中看到它（或类似的东西）。

关于包含批归一化层的模型的一个有趣观察是，它们往往比不包含批归一化层的模型更好地泛化。尽管我们尚未看到对这里发生的事情进行严格分析，但大多数研究人员认为原因是批归一化为训练过程添加了一些额外的随机性。每个小批次的均值和标准差都会与其他小批次有所不同。因此，激活每次都会被不同的值归一化。为了使模型能够做出准确的预测，它必须学会对这些变化变得稳健。通常，向训练过程添加额外的随机性通常有所帮助。

由于事情进展顺利，让我们再训练几个周期，看看情况如何。实际上，让我们增加学习率，因为批归一化论文的摘要声称我们应该能够“以更高的学习率训练”：

learn = fit(5, lr=0.1)

epoch	train_loss	valid_loss	accuracy	time
0	0.191731	0.121738	0.960900	00:11
1	0.083739	0.055808	0.981800	00:10
2	0.053161	0.044485	0.987100	00:10
3	0.034433	0.030233	0.990200	00:10
4	0.017646	0.025407	0.991200	00:10

learn = fit(5, lr=0.1)

epoch	train_loss	valid_loss	accuracy	time
0	0.183244	0.084025	0.975800	00:13
1	0.080774	0.067060	0.978800	00:12
2	0.050215	0.062595	0.981300	00:12
3	0.030020	0.030315	0.990700	00:12
4	0.015131	0.025148	0.992100	00:12

在这一点上，我认为我们知道如何识别数字了！是时候转向更难的东西了…

结论

我们已经看到，卷积只是一种矩阵乘法，对权重矩阵有两个约束：一些元素始终为零，一些元素被绑定（强制始终具有相同的值）。在第一章中，我们看到了 1986 年书籍并行分布式处理中的八个要求；其中之一是“单元之间的连接模式”。这正是这些约束所做的：它们强制执行一定的连接模式。

这些约束允许我们在不牺牲表示复杂视觉特征的能力的情况下，在模型中使用更少的参数。这意味着我们可以更快地训练更深的模型，减少过拟合。尽管普遍逼近定理表明在一个隐藏层中应该可能用全连接网络表示任何东西，但我们现在看到，通过深思熟虑网络架构，我们可以训练出更好的模型。

卷积是我们在神经网络中看到的最常见的连接模式（连同常规线性层，我们称之为全连接），但很可能会发现更多。

我们还看到了如何解释网络中各层的激活，以查看训练是否顺利，以及批归一化如何帮助规范训练并使其更加平滑。在下一章中，我们将使用这两个层来构建计算机视觉中最流行的架构：残差网络。

问卷

特征是什么？
为顶部边缘检测器编写卷积核矩阵。
写出 3×3 卷积核对图像中单个像素应用的数学运算。
应用于 3×3 零矩阵的卷积核的值是多少？
填充是什么？
步幅是什么？
创建一个嵌套列表推导来完成您选择的任何任务。
PyTorch 的 2D 卷积的input和weight参数的形状是什么？
通道是什么？
卷积和矩阵乘法之间的关系是什么？
卷积神经网络是什么？
重构神经网络定义的部分有什么好处？
什么是Flatten？MNIST CNN 中需要包含在哪里？为什么？
NCHW 是什么意思？
为什么 MNIST CNN 的第三层有7*7*(1168-16)次乘法运算？
什么是感受野？
经过两次步幅为 2 的卷积后，激活的感受野大小是多少？为什么？
自己运行conv-example.xlsx并尝试使用trace precedents进行实验。
看一下 Jeremy 或 Sylvain 最近的 Twitter“喜欢”列表，看看是否有任何有趣的资源或想法。
彩色图像如何表示为张量？
彩色输入下卷积是如何工作的？
我们可以使用什么方法来查看DataLoaders中的数据？
为什么我们在每次步幅为 2 的卷积后将滤波器数量加倍？
为什么在 MNIST 的第一个卷积中使用较大的内核（使用simple_cnn）？
ActivationStats为每个层保存了什么信息？
在训练后如何访问学习者的回调？
plot_layer_stats绘制了哪三个统计数据？x 轴代表什么？
为什么接近零的激活是有问题的？
使用更大的批量大小进行训练的优缺点是什么？
为什么我们应该避免在训练开始时使用高学习率？
什么是 1cycle 训练？
使用高学习率进行训练的好处是什么？
为什么我们希望在训练结束时使用较低的学习率？
什么是循环动量？
哪个回调在训练期间跟踪超参数值（以及其他信息）？
color_dim图中的一列像素代表什么？
在color_dim中，“坏训练”是什么样子？为什么？
批规范化层包含哪些可训练参数？
在训练期间批规范化使用哪些统计数据进行规范化？验证期间呢？
为什么具有批规范化层的模型泛化能力更好？

进一步研究

除了边缘检测器，计算机视觉中还使用了哪些特征（尤其是在深度学习变得流行之前）？
PyTorch 中还有其他规范化层。尝试它们，看看哪种效果最好。了解其他规范化层的开发原因以及它们与批规范化的区别。
尝试将激活函数移动到conv中的批规范化层后。这会有所不同吗？看看你能找到关于推荐顺序及原因的信息。

第十四章：ResNets

原文：www.bookstack.cn/read/th-fastai-book/482a7208820b3d90.md

译者：飞龙

协议：CC BY-NC-SA 4.0

在本章中，我们将在上一章介绍的 CNN 基础上构建，并向您解释 ResNet（残差网络）架构。它是由 Kaiming He 等人于 2015 年在文章“Deep Residual Learning for Image Recognition”中引入的，到目前为止是最常用的模型架构。最近在图像模型中的发展几乎总是使用残差连接的相同技巧，大多数时候，它们只是原始 ResNet 的调整。

我们将首先展示最初设计的基本 ResNet，然后解释使其性能更好的现代调整。但首先，我们需要一个比 MNIST 数据集更难一点的问题，因为我们已经在常规 CNN 上接近 100%的准确率了。

回到 Imagenette

当我们已经在上一章的 MNIST 中看到的准确率已经很高时，要评估我们对模型的任何改进将会很困难，因此我们将通过回到 Imagenette 来解决一个更困难的图像分类问题。我们将继续使用小图像以保持事情相对快速。

让我们获取数据——我们将使用已经调整大小为 160 像素的版本以使事情更快，然后将随机裁剪到 128 像素：

def get_data(url, presize, resize):
    path = untar_data(url)
    return DataBlock(
        blocks=(ImageBlock, CategoryBlock), get_items=get_image_files,
        splitter=GrandparentSplitter(valid_name='val'),
        get_y=parent_label, item_tfms=Resize(presize),
        batch_tfms=[*aug_transforms(min_scale=0.5, size=resize),
                    Normalize.from_stats(*imagenet_stats)],
    ).dataloaders(path, bs=128)

dls = get_data(URLs.IMAGENETTE_160, 160, 128)

dls.show_batch(max_n=4)

当我们查看 MNIST 时，我们处理的是 28×28 像素的图像。对于 Imagenette，我们将使用 128×128 像素的图像进行训练。稍后，我们希望能够使用更大的图像，至少与 224×224 像素的 ImageNet 标准一样大。您还记得我们如何从 MNIST 卷积神经网络中获得每个图像的单个激活向量吗？

我们采用的方法是确保有足够的步幅为 2 的卷积，以使最终层具有 1 的网格大小。然后我们展平我们最终得到的单位轴，为每个图像获得一个向量（因此，对于一个小批量的激活矩阵）。我们可以对 Imagenette 做同样的事情，但这会导致两个问题：

我们需要很多步幅为 2 的层，才能使我们的网格在最后变成 1×1 的大小——可能比我们本来会选择的要多。
该模型将无法处理除最初训练的大小之外的任何大小的图像。

处理第一个问题的一种方法是以一种处理 1×1 以外的网格大小的方式展平最终的卷积层。我们可以简单地将矩阵展平为向量，就像我们以前做过的那样，通过将每一行放在前一行之后。事实上，这是卷积神经网络直到 2013 年几乎总是采用的方法。最著名的例子是 2013 年 ImageNet 的获奖者 VGG，有时今天仍在使用。但这种架构还有另一个问题：它不仅不能处理与训练集中使用的相同大小的图像之外的图像，而且需要大量内存，因为展平卷积层导致许多激活被馈送到最终层。因此，最终层的权重矩阵是巨大的。

这个问题通过创建完全卷积网络来解决。完全卷积网络的技巧是对卷积网格中的激活进行平均。换句话说，我们可以简单地使用这个函数：

def avg_pool(x): return x.mean((2,3))

正如您所看到的，它正在计算 x 轴和 y 轴上的平均值。这个函数将始终将一组激活转换为每个图像的单个激活。PyTorch 提供了一个稍微更灵活的模块，称为nn.AdaptiveAvgPool2d，它将一组激活平均到您需要的任何大小的目标（尽管我们几乎总是使用大小为 1）。

因此，一个完全卷积网络具有多个卷积层，其中一些将是步幅为 2 的，在最后是一个自适应平均池化层，一个展平层来移除单位轴，最后是一个线性层。这是我们的第一个完全卷积网络：

def block(ni, nf): return ConvLayer(ni, nf, stride=2)
def get_model():
    return nn.Sequential(
        block(3, 16),
        block(16, 32),
        block(32, 64),
        block(64, 128),
        block(128, 256),
        nn.AdaptiveAvgPool2d(1),
        Flatten(),
        nn.Linear(256, dls.c))

我们将在网络中用其他变体替换block的实现，这就是为什么我们不再称其为conv。我们还通过利用 fastai 的ConvLayer节省了一些时间，它已经提供了前一章中conv的功能（还有更多！）。

停下来思考

考虑这个问题：这种方法对于像 MNIST 这样的光学字符识别（OCR）问题是否有意义？绝大多数从事 OCR 和类似问题的从业者倾向于使用全卷积网络，因为这是现在几乎每个人都学习的。但这真的毫无意义！例如，你不能通过将数字切成小块、混在一起，然后决定每个块平均看起来像 3 还是 8 来判断一个数字是 3 还是 8。但这正是自适应平均池化有效地做的事情！全卷积网络只对没有单一正确方向或大小的对象（例如大多数自然照片）是一个很好的选择。

一旦我们完成卷积层，我们将得到大小为bs x ch x h x w的激活（批量大小、一定数量的通道、高度和宽度）。我们想将其转换为大小为bs x ch的张量，因此我们取最后两个维度的平均值，并像在我们之前的模型中那样展平尾随的 1×1 维度。

这与常规池化不同，因为这些层通常会取给定大小窗口的平均值（对于平均池化）或最大值（对于最大池化）。例如，大小为 2 的最大池化层在旧的 CNN 中非常流行，通过在每个维度上取每个 2×2 窗口的最大值（步幅为 2），将图像的尺寸减半。

与以前一样，我们可以使用我们自定义的模型定义一个Learner，然后在之前获取的数据上对其进行训练：

def get_learner(m):
    return Learner(dls, m, loss_func=nn.CrossEntropyLoss(), metrics=accuracy
                  ).to_fp16()

learn = get_learner(get_model())

learn.lr_find()

(0.47863011360168456, 3.981071710586548)

对于 CNN 来说，3e-3 通常是一个很好的学习率，这在这里也是如此，所以让我们试一试：

learn.fit_one_cycle(5, 3e-3)

epoch	train_loss	valid_loss	accuracy	time
0	1.901582	2.155090	0.325350	00:07
1	1.559855	1.586795	0.507771	00:07
2	1.296350	1.295499	0.571720	00:07
3	1.144139	1.139257	0.639236	00:07
4	1.049770	1.092619	0.659108	00:07

考虑到我们必须从头开始选择 10 个类别中的正确一个，而且我们只训练了 5 个时期，这是一个相当不错的开始！我们可以通过使用更深的模型做得更好，但只是堆叠新层并不会真正改善我们的结果（你可以尝试自己看看！）。为了解决这个问题，ResNets 引入了跳跃连接的概念。我们将在下一节中探讨 ResNets 的这些方面。

构建现代 CNN：ResNet

我们现在已经拥有构建我们自从本书开始就一直在计算机视觉任务中使用的模型所需的所有要素：ResNets。我们将介绍它们背后的主要思想，并展示它如何在 Imagenette 上提高了准确性，然后构建一个带有所有最新调整的版本。

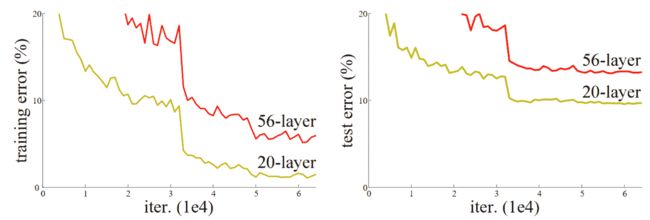
跳跃连接

2015 年，ResNet 论文的作者们注意到了一件他们觉得奇怪的事情。即使使用了批量归一化，他们发现使用更多层的网络表现不如使用更少层的网络，并且模型之间没有其他差异。最有趣的是，这种差异不仅在验证集中观察到，而且在训练集中也观察到；因此这不仅仅是一个泛化问题，而是一个训练问题。正如论文所解释的：

出乎意料的是，这种退化并不是由过拟合引起的，向适当深度的模型添加更多层会导致更高的训练错误，正如我们的实验[先前报告]和彻底验证的那样。

这种现象在图 14-1 中的图表中有所说明，左侧是训练错误，右侧是测试错误。

图 14-1。不同深度网络的训练（由 Kaiming He 等人提供）。

正如作者在这里提到的，他们并不是第一个注意到这个奇怪事实的人。但他们是第一个迈出非常重要的一步：

让我们考虑一个更浅的架构及其更深的对应物，后者在其上添加更多层。存在一种通过构建解决更深模型的方法：添加的层是恒等映射，其他层是从学习的更浅模型中复制的。

由于这是一篇学术论文，这个过程以一种不太易懂的方式描述，但概念实际上非常简单：从一个训练良好的 20 层神经网络开始，然后添加另外 36 层什么都不做的层（例如，它们可以是具有单个权重等于 1 和偏置等于 0 的线性层）。结果将是一个 56 层的网络，它与 20 层网络完全相同，证明总是存在深度网络应该至少和任何浅层网络一样好。但由于某种原因，随机梯度下降似乎无法找到它们。

行话：恒等映射

将输入返回而不做任何改变。这个过程由一个恒等函数执行。

实际上，还有另一种更有趣的方法来创建这些额外的 36 层。如果我们用x + conv(x)替换每次出现的conv(x)，其中conv是上一章中添加第二个卷积，然后是 ReLU，然后是批量归一化层的函数。此外，回想一下批量归一化是gamma*y + beta。如果我们为这些最终批量归一化层中的每一个初始化gamma为零会怎样？那么我们这些额外的 36 层的conv(x)将始终等于零，这意味着x+conv(x)将始终等于x。

这给我们带来了什么好处？关键是，这 36 个额外的层，就目前而言，是一个恒等映射，但它们有参数，这意味着它们是可训练的。因此，我们可以从最好的 20 层模型开始，添加这 36 个最初什么都不做的额外层，然后微调整个 56 层模型。这些额外的 36 层可以学习使它们最有用的参数！

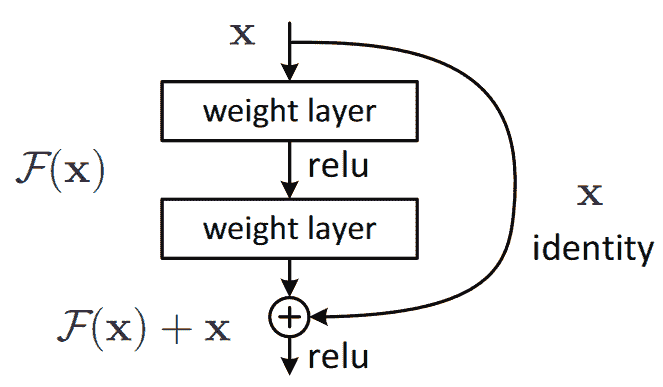
ResNet 论文提出了这样的一个变体，即“跳过”每第二个卷积，因此我们实际上得到了x+conv2(conv1(x))。这在图 14-2（来自论文）中的图表中显示。

图 14-2。一个简单的 ResNet 块（由 Kaiming He 等人提供）。

右侧的箭头只是x+conv2(conv1(x))中的x部分，被称为恒等分支或跳跃连接。左侧路径是conv2(conv1(x))部分。您可以将恒等路径视为提供从输入到输出的直接路径。

在 ResNet 中，我们不是先训练少量层，然后在末尾添加新层并进行微调。相反，我们在整个 CNN 中使用像图 14-2 中的 ResNet 块这样的块，以通常的方式从头开始初始化并以通常的方式使用 SGD 进行训练。我们依靠跳跃连接使网络更容易使用 SGD 进行训练。

还有另一种（在很大程度上等效的）思考这些 ResNet 块的方式。这就是论文描述的方式：

我们不是希望每几个堆叠的层直接适应所需的底层映射，而是明确让这些层适应一个残差映射。形式上，将所需的底层映射表示为H(x)，我们让堆叠的非线性层适应另一个映射F(x) := H(x)−x。原始映射被重新构造为F(x)+x。我们假设优化残差映射比优化原始未引用的映射更容易。在极端情况下，如果恒等映射是最佳的，将残差推向零将比通过一堆非线性层适应恒等映射更容易。

再次，这是相当晦涩的文字，让我们尝试用简单的英语重新表述一下！如果给定层的结果是x，我们使用一个返回y = x + block(x)的 ResNet 块，我们不是要求该块预测y；我们要求它预测y和x之间的差异。因此，这些块的任务不是预测特定的特征，而是最小化x和期望的y之间的误差。因此，ResNet 擅长学习不做任何事情和通过两个卷积层块（具有可训练权重）之间的区别。这就是这些模型得名的原因：它们在预测残差（提醒：“残差”是预测减去目标）。

这两种关于 ResNet 的思考方式共享的一个关键概念是学习的便利性。这是一个重要的主题。回想一下普遍逼近定理，它指出一个足够大的网络可以学习任何东西。这仍然是真的，但事实证明，在原始数据和训练方案下，网络在原则上可以学习的东西与它实际上容易学习的东西之间存在非常重要的区别。过去十年中神经网络的许多进步都像 ResNet 块一样：意识到如何使一些一直可能的东西变得可行。

真实身份路径

原始论文实际上并没有在每个块的最后一个 batchnorm 层中使用零作为gamma的初始值的技巧；这是几年后才出现的。因此，ResNet 的原始版本并没有真正以真实的身份路径开始训练 ResNet 块，但是尽管如此，具有“穿越”跳过连接的能力确实使其训练效果更好。添加 batchnorm gamma初始化技巧使模型能够以更高的学习速率训练。

这是一个简单 ResNet 块的定义（fastai 将最后一个 batchnorm 层的gamma权重初始化为零，因为norm_type=NormType.BatchZero）：

class ResBlock(Module):
    def __init__(self, ni, nf):
        self.convs = nn.Sequential(
            ConvLayer(ni,nf),
            ConvLayer(nf,nf, norm_type=NormType.BatchZero))

    def forward(self, x): return x + self.convs(x)

然而，这有两个问题：它无法处理除 1 以外的步幅，并且要求ni==nf。停下来仔细思考为什么会这样。

问题在于，如果在其中一个卷积层上使用步幅为 2，输出激活的网格大小将是输入的每个轴的一半。因此，我们无法将其添加回forward中的x，因为x和输出激活具有不同的维度。如果ni!=nf，则会出现相同的基本问题：输入和输出连接的形状不允许我们将它们相加。

为了解决这个问题，我们需要一种方法来改变x的形状，使其与self.convs的结果匹配。可以通过使用步幅为 2 的平均池化层来减半网格大小：也就是说，该层从输入中获取 2×2 的块，并用它们的平均值替换它们。

可以通过使用卷积来改变通道数。然而，我们希望这个跳过连接尽可能接近一个恒等映射，这意味着使这个卷积尽可能简单。最简单的卷积是一个卷积核大小为 1 的卷积。这意味着卷积核大小为ni × nf × 1 × 1，因此它只是对每个输入像素的通道进行点积运算，根本不跨像素进行组合。这种1x1 卷积在现代 CNN 中被广泛使用，因此花一点时间思考它是如何工作的。

术语：1x1 卷积

卷积核大小为 1 的卷积。

以下是使用这些技巧处理跳过连接中形状变化的 ResBlock：

def _conv_block(ni,nf,stride):
    return nn.Sequential(
        ConvLayer(ni, nf, stride=stride),
        ConvLayer(nf, nf, act_cls=None, norm_type=NormType.BatchZero))

class ResBlock(Module):
    def __init__(self, ni, nf, stride=1):
        self.convs = _conv_block(ni,nf,stride)
        self.idconv = noop if ni==nf else ConvLayer(ni, nf, 1, act_cls=None)
        self.pool = noop if stride==1 else nn.AvgPool2d(2, ceil_mode=True)

    def forward(self, x):
        return F.relu(self.convs(x) + self.idconv(self.pool(x)))

请注意，我们在这里使用noop函数，它只是返回其未更改的输入（noop是一个计算机科学术语，代表“无操作”）。在这种情况下，如果nf==nf，idconv什么也不做，如果stride==1，pool也不做任何操作，这正是我们在跳过连接中想要的。

此外，您会看到我们已经从convs的最后一个卷积层和idconv中删除了 ReLU（act_cls=None），并将其移到在我们添加跳跃连接之后。这样做的想法是整个 ResNet 块就像一个层，您希望激活在层之后。

让我们用ResBlock替换我们的block并尝试一下：

def block(ni,nf): return ResBlock(ni, nf, stride=2)
learn = get_learner(get_model())

learn.fit_one_cycle(5, 3e-3)

epoch	train_loss	valid_loss	accuracy	time
0	1.973174	1.845491	0.373248	00:08
1	1.678627	1.778713	0.439236	00:08
2	1.386163	1.596503	0.507261	00:08
3	1.177839	1.102993	0.644841	00:09
4	1.052435	1.038013	0.667771	00:09

这并没有好多少。但这一切的目的是让我们能够训练更深的模型，而我们实际上还没有充分利用这一点。要创建一个比如说深两倍的模型，我们只需要用两个ResBlock替换我们的block：

def block(ni, nf):
    return nn.Sequential(ResBlock(ni, nf, stride=2), ResBlock(nf, nf))

learn = get_learner(get_model())
learn.fit_one_cycle(5, 3e-3)

epoch	train_loss	valid_loss	accuracy	time
0	1.964076	1.864578	0.355159	00:12
1	1.636880	1.596789	0.502675	00:12
2	1.335378	1.304472	0.588535	00:12
3	1.089160	1.065063	0.663185	00:12
4	0.942904	0.963589	0.692739	00:12

现在我们取得了良好的进展！

ResNet 论文的作者后来赢得了 2015 年 ImageNet 挑战赛。当时，这是计算机视觉领域迄今为止最重要的年度事件。我们已经看到另一个 ImageNet 的获奖者：2013 年的获奖者 Zeiler 和 Fergus。值得注意的是，在这两种情况下，突破的起点都是实验观察：Zeiler 和 Fergus 案例中关于层实际学习内容的观察，以及 ResNet 作者案例中关于可以训练哪种网络的观察。设计和分析周到的实验，甚至只是看到一个意想不到的结果，然后，最重要的是，开始弄清楚到底发生了什么，具有极大的坚韧性，这是许多科学发现的核心。深度学习不像纯数学。这是一个非常实验性的领域，因此成为一个强大的实践者，而不仅仅是一个理论家，是非常重要的。

自 ResNet 推出以来，它已经被广泛研究和应用于许多领域。其中最有趣的论文之一，发表于 2018 年，是由 Hao Li 等人撰写的“可视化神经网络损失景观”。它表明使用跳跃连接有助于平滑损失函数，这使得训练更容易，因为它避免了陷入非常陡峭的区域。图 14-3 展示了该论文中的一幅惊人图片，说明了 SGD 需要导航以优化普通 CNN（左侧）与 ResNet（右侧）之间的不同之处。

图 14-3. ResNet 对损失景观的影响（由 Hao Li 等人提供）

我们的第一个模型已经很好了，但进一步的研究发现了更多可以应用的技巧，使其变得更好。我们接下来将看看这些技巧。

一个最先进的 ResNet

在“用卷积神经网络进行图像分类的技巧”中，Tong He 等人研究了 ResNet 架构的变体，这几乎没有额外的参数或计算成本。通过使用调整后的 ResNet-50 架构和 Mixup，他们在 ImageNet 上实现了 94.6%的 Top-5 准确率，而普通的 ResNet-50 没有 Mixup 只有 92.2%。这个结果比普通 ResNet 模型取得的结果更好，后者深度是它的两倍（速度也是两倍，更容易过拟合）。

术语：Top-5 准确率

一个度量，测试我们模型的前 5 个预测中我们想要的标签有多少次。在 ImageNet 竞赛中使用它，因为许多图像包含多个对象，或者包含可以轻松混淆甚至可能被错误标记为相似标签的对象。在这些情况下，查看前 1 的准确率可能不合适。然而，最近 CNN 的表现越来越好，以至于前 5 的准确率几乎达到 100%，因此一些研究人员现在也在 ImageNet 中使用前 1 的准确率。

当我们扩展到完整的 ResNet 时，我们将使用这个调整过的版本，因为它要好得多。它与我们之前的实现略有不同，它不是直接从 ResNet 块开始，而是从几个卷积层开始，然后是一个最大池化层。这就是网络的第一层，称为干的样子：

def _resnet_stem(*sizes):
    return [
        ConvLayer(sizes[i], sizes[i+1], 3, stride = 2 if i==0 else 1)
            for i in range(len(sizes)-1)
    ] + [nn.MaxPool2d(kernel_size=3, stride=2, padding=1)]

_resnet_stem(3,32,32,64)

[ConvLayer(
   (0): Conv2d(3, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
   (1): BatchNorm2d(32, eps=1e-05, momentum=0.1)
   (2): ReLU()
 ), ConvLayer(
   (0): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
   (1): BatchNorm2d(32, eps=1e-05, momentum=0.1)
   (2): ReLU()
 ), ConvLayer(
   (0): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
   (1): BatchNorm2d(64, eps=1e-05, momentum=0.1)
   (2): ReLU()
 ), MaxPool2d(kernel_size=3, stride=2, padding=1, ceil_mode=False)]

术语：干

CNN 的前几层。通常，干的结构与 CNN 的主体不同。

我们之所以有一系列普通卷积层的起始，而不是 ResNet 块，是基于对所有深度卷积神经网络的一个重要洞察：绝大部分的计算发生在早期层。因此，我们应该尽可能保持早期层的速度和简单。

要了解为什么绝大部分的计算发生在早期层，考虑一下在 128 像素输入图像上的第一个卷积。如果是步幅为 1 的卷积，它将应用核到 128×128 个像素中的每一个。这是很多工作！然而，在后续层中，网格大小可能只有 4×4 甚至 2×2，因此要做的核应用要少得多。

另一方面，第一层卷积只有 3 个输入特征和 32 个输出特征。由于它是一个 3×3 的核，这是权重中的 864 个参数。但最后一个卷积将有 256 个输入特征和 512 个输出特征，导致 1,179,648 个权重！因此，第一层包含了绝大部分的计算量，而最后几层包含了绝大部分的参数。

一个 ResNet 块比一个普通卷积块需要更多的计算，因为（在步幅为 2 的情况下）一个 ResNet 块有三个卷积和一个池化层。这就是为什么我们希望从普通卷积开始我们的 ResNet。

现在我们准备展示一个现代 ResNet 的实现，带有“技巧袋”。它使用了四组 ResNet 块，分别为 64、128、256 和 512 个滤波器。每组都以步幅为 2 的块开始，除了第一组，因为它紧接着一个MaxPooling层：

class ResNet(nn.Sequential):
    def __init__(self, n_out, layers, expansion=1):
        stem = _resnet_stem(3,32,32,64)
        self.block_szs = [64, 64, 128, 256, 512]
        for i in range(1,5): self.block_szs[i] *= expansion
        blocks = [self._make_layer(*o) for o in enumerate(layers)]
        super().__init__(*stem, *blocks,
                         nn.AdaptiveAvgPool2d(1), Flatten(),
                         nn.Linear(self.block_szs[-1], n_out))

    def _make_layer(self, idx, n_layers):
        stride = 1 if idx==0 else 2
        ch_in,ch_out = self.block_szs[idx:idx+2]
        return nn.Sequential(*[
            ResBlock(ch_in if i==0 else ch_out, ch_out, stride if i==0 else 1)
            for i in range(n_layers)
        ])

_make_layer函数只是用来创建一系列n_layers块。第一个是从ch_in到ch_out，步幅为指定的stride，其余所有块都是步幅为 1 的块，从ch_out到ch_out张量。一旦块被定义，我们的模型就是纯顺序的，这就是为什么我们将其定义为nn.Sequential的子类。（暂时忽略expansion参数；我们将在下一节讨论它。暂时设为1，所以它不起作用。）

模型的各个版本（ResNet-18、-34、-50 等）只是改变了每个组中块的数量。这是 ResNet-18 的定义：

rn = ResNet(dls.c, [2,2,2,2])

让我们训练一下，看看它与之前的模型相比如何：

learn = get_learner(rn)
learn.fit_one_cycle(5, 3e-3)

epoch	train_loss	valid_loss	accuracy	time
0	1.673882	1.828394	0.413758	00:13
1	1.331675	1.572685	0.518217	00:13
2	1.087224	1.086102	0.650701	00:13
3	0.900428	0.968219	0.684331	00:12
4	0.760280	0.782558	0.757197	00:12

尽管我们有更多的通道（因此我们的模型更准确），但由于我们优化了干，我们的训练速度与以前一样快。

为了使我们的模型更深，而不占用太多计算或内存，我们可以使用 ResNet 论文引入的另一种层：瓶颈层。

瓶颈层

瓶颈层不是使用 3 个内核大小为 3 的卷积堆叠，而是使用三个卷积：两个 1×1（在开头和结尾）和一个 3×3，如右侧在图 14-4 中所示。

图 14-4. 常规和瓶颈 ResNet 块的比较（由 Kaiming He 等人提供）

为什么这很有用？1×1 卷积速度更快，因此即使这似乎是一个更复杂的设计，这个块的执行速度比我们看到的第一个 ResNet 块更快。这样一来，我们可以使用更多的滤波器：正如我们在插图中看到的，输入和输出的滤波器数量是四倍更高的（256 而不是 64）。1×1 卷积减少然后恢复通道数（因此称为瓶颈）。总体影响是我们可以在相同的时间内使用更多的滤波器。

让我们尝试用这种瓶颈设计替换我们的ResBlock：

def _conv_block(ni,nf,stride):
    return nn.Sequential(
        ConvLayer(ni, nf//4, 1),
        ConvLayer(nf//4, nf//4, stride=stride),
        ConvLayer(nf//4, nf, 1, act_cls=None, norm_type=NormType.BatchZero))

我们将使用这个来创建一个具有组大小(3,4,6,3)的 ResNet-50。现在我们需要将4传递给ResNet的expansion参数，因为我们需要从四倍少的通道开始，最终将以四倍多的通道结束。

像这样更深的网络通常在仅训练 5 个时期时不会显示出改进，所以这次我们将将其增加到 20 个时期，以充分利用我们更大的模型。为了获得更好的结果，让我们也使用更大的图像：

dls = get_data(URLs.IMAGENETTE_320, presize=320, resize=224)

我们不必为更大的 224 像素图像做任何调整；由于我们的全卷积网络，它可以正常工作。这也是为什么我们能够在本书的早期进行渐进调整的原因——我们使用的模型是全卷积的，所以我们甚至能够微调使用不同尺寸训练的模型。现在我们可以训练我们的模型并查看效果：

rn = ResNet(dls.c, [3,4,6,3], 4)

learn = get_learner(rn)
learn.fit_one_cycle(20, 3e-3)

epoch	train_loss	valid_loss	accuracy	time
0	1.613448	1.473355	0.514140	00:31
1	1.359604	2.050794	0.397452	00:31
2	1.253112	4.511735	0.387006	00:31
3	1.133450	2.575221	0.396178	00:31
4	1.054752	1.264525	0.613758	00:32
5	0.927930	2.670484	0.422675	00:32
6	0.838268	1.724588	0.528662	00:32
7	0.748289	1.180668	0.666497	00:31
8	0.688637	1.245039	0.650446	00:32
9	0.645530	1.053691	0.674904	00:31
10	0.593401	1.180786	0.676433	00:32
11	0.536634	0.879937	0.713885	00:32
12	0.479208	0.798356	0.741656	00:32
13	0.440071	0.600644	0.806879	00:32
14	0.402952	0.450296	0.858599	00:32
15	0.359117	0.486126	0.846369	00:32
16	0.313642	0.442215	0.861911	00:32
17	0.294050	0.485967	0.853503	00:32
18	0.270583	0.408566	0.875924	00:32
19	0.266003	0.411752	0.872611	00:33

现在我们得到了一个很好的结果！尝试添加 Mixup，然后在吃午餐时将其训练一百个时期。你将拥有一个从头开始训练的非常准确的图像分类器。

这里展示的瓶颈设计通常仅用于 ResNet-50、-101 和-152 模型。ResNet-18 和-34 模型通常使用前一节中看到的非瓶颈设计。然而，我们注意到瓶颈层通常即使对于较浅的网络也效果更好。这只是表明，论文中的细节往往会持续多年，即使它们并不是最佳设计！质疑假设和“每个人都知道的东西”总是一个好主意，因为这仍然是一个新领域，很多细节并不总是做得很好。

结论

自第一章以来，我们一直在使用的计算机视觉模型是如何构建的，使用跳跃连接来训练更深的模型。尽管已经进行了大量研究以寻找更好的架构，但它们都使用这个技巧的某个版本来建立从输入到网络末端的直接路径。在使用迁移学习时，ResNet 是预训练模型。在下一章中，我们将看一下我们使用的模型是如何从中构建的最终细节。

问卷调查

在以前的章节中，我们如何将用于 MNIST 的 CNN 转换为单个激活向量？为什么这对 Imagenette 不适用？
我们在 Imagenette 上做了什么？
什么是自适应池化？
什么是平均池化？
为什么在自适应平均池化层之后需要Flatten？
什么是跳跃连接？
为什么跳跃连接使我们能够训练更深的模型？
图 14-1 展示了什么？这是如何导致跳跃连接的想法的？
什么是恒等映射？
ResNet 块的基本方程是什么（忽略批量归一化和 ReLU 层）？
ResNet 与残差有什么关系？
当存在步幅为 2 的卷积时，我们如何处理跳跃连接？当滤波器数量发生变化时呢？
我们如何用向量点积表示 1×1 卷积？
使用F.conv2d或nn.Conv2d创建一个 1×1 卷积并将其应用于图像。图像的形状会发生什么变化？
noop函数返回什么？
解释图 14-3 中显示的内容。
何时使用前 5 准确度比前 1 准确度更好？
CNN 的“起始”是什么？
为什么在 CNN 的起始部分使用普通卷积而不是 ResNet 块？
瓶颈块与普通 ResNet 块有何不同？
为什么瓶颈块更快？
完全卷积网络（以及具有自适应池化的网络）如何实现渐进式调整大小？

进一步研究

尝试为 MNIST 创建一个带有自适应平均池化的完全卷积网络（请注意，您将需要更少的步幅为 2 的层）。与没有这种池化层的网络相比如何？
在第十七章中，我们介绍了爱因斯坦求和符号。快进去看看它是如何工作的，然后使用torch.einsum编写一个 1×1 卷积操作的实现。将其与使用torch.conv2d进行相同操作进行比较。
使用纯 PyTorch 或纯 Python 编写一个前 5 准确度函数。
在 Imagenette 上训练一个模型更多的 epochs，使用和不使用标签平滑。查看 Imagenette 排行榜，看看你能达到最佳结果有多接近。阅读描述领先方法的链接页面。

第十五章：应用架构深入探讨

原文：www.bookstack.cn/read/th-fastai-book/fc209e8bb92c8c12.md

译者：飞龙

协议：CC BY-NC-SA 4.0

我们现在处于一个令人兴奋的位置，我们可以完全理解我们为计算机视觉、自然语言处理和表格分析使用的最先进模型的架构。在本章中，我们将填补有关 fastai 应用模型如何工作的所有缺失细节，并向您展示如何构建它们。

我们还将回到我们在第十一章中看到的用于 Siamese 网络的自定义数据预处理流程，并向您展示如何使用 fastai 库中的组件为新任务构建自定义预训练模型。

我们将从计算机视觉开始。

计算机视觉

对于计算机视觉应用，我们使用cnn_learner和unet_learner函数来构建我们的模型，具体取决于任务。在本节中，我们将探讨如何构建我们在本书的第 I 部分和 II 部分中使用的Learner对象。

cnn_learner

让我们看看当我们使用cnn_learner函数时会发生什么。我们首先向这个函数传递一个用于网络主体的架构。大多数情况下，我们使用 ResNet，您已经知道如何创建，所以我们不需要深入研究。预训练权重将根据需要下载并加载到 ResNet 中。

然后，对于迁移学习，网络需要被切割。这指的是切掉最后一层，该层仅负责 ImageNet 特定的分类。实际上，我们不仅切掉这一层，还切掉自自适应平均池化层以及之后的所有内容。这样做的原因很快就会变得清楚。由于不同的架构可能使用不同类型的池化层，甚至完全不同类型的头部，我们不仅仅搜索自适应池化层来决定在哪里切割预训练模型。相反，我们有一个信息字典，用于确定每个模型的主体在哪里结束，头部从哪里开始。我们称之为model_meta—这是resnet50的信息：

model_meta[resnet50]

{'cut': -2,
 'split': <function fastai.vision.learner._resnet_split(m)>,
 'stats': ([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])}

行话：主体和头部

神经网络的头部是专门针对特定任务的部分。对于 CNN，通常是自适应平均池化层之后的部分。主体是其他所有部分，包括干部（我们在第十四章中学到的）。

如果我们取出在-2之前的所有层，我们就得到了 fastai 将保留用于迁移学习的模型部分。现在，我们放上我们的新头部。这是使用create_head函数创建的：

create_head(20,2)

Sequential(
  (0): AdaptiveConcatPool2d(
    (ap): AdaptiveAvgPool2d(output_size=1)
    (mp): AdaptiveMaxPool2d(output_size=1)
  )
  (1): Flatten()
  (2): BatchNorm1d(20, eps=1e-05, momentum=0.1, affine=True)
  (3): Dropout(p=0.25, inplace=False)
  (4): Linear(in_features=20, out_features=512, bias=False)
  (5): ReLU(inplace=True)
  (6): BatchNorm1d(512, eps=1e-05, momentum=0.1, affine=True)
  (7): Dropout(p=0.5, inplace=False)
  (8): Linear(in_features=512, out_features=2, bias=False)
)

使用这个函数，您可以选择在末尾添加多少个额外的线性层，每个线性层之后使用多少 dropout，以及使用什么类型的池化。默认情况下，fastai 将同时应用平均池化和最大池化，并将两者连接在一起（这是AdaptiveConcatPool2d层）。这不是一个特别常见的方法，但它在 fastai 和其他研究实验室近年来独立开发，并倾向于比仅使用平均池化提供小幅改进。

fastai 与大多数库有所不同，因为默认情况下它在 CNN 头部中添加两个线性层，而不是一个。原因是，正如我们所看到的，即使将预训练模型转移到非常不同的领域，迁移学习仍然可能是有用的。然而，在这些情况下，仅使用单个线性层可能不足够；我们发现使用两个线性层可以使迁移学习更快速、更容易地应用在更多情况下。

最后一个 Batchnorm

create_head的一个值得关注的参数是bn_final。将其设置为True将导致一个 batchnorm 层被添加为您的最终层。这有助于帮助您的模型适当地缩放输出激活。迄今为止，我们还没有看到这种方法在任何地方发表，但我们发现在实践中无论我们在哪里使用它，它都效果很好。

现在让我们看看unet_learner在我们在第一章展示的分割问题中做了什么。

unet_learner

深度学习中最有趣的架构之一是我们在第一章中用于分割的架构。分割是一项具有挑战性的任务，因为所需的输出实际上是一幅图像，或者一个像素网格，包含了每个像素的预测标签。其他任务也有类似的基本设计，比如增加图像的分辨率（超分辨率）、给黑白图像添加颜色（着色）、或将照片转换为合成画作（风格转移）——这些任务在本书的在线章节中有介绍，所以在阅读完本章后一定要查看。在每种情况下，我们都是从一幅图像开始，将其转换为另一幅具有相同尺寸或纵横比的图像，但像素以某种方式被改变。我们将这些称为生成式视觉模型。

我们的做法是从与前一节中看到的开发 CNN 头部的确切方法开始。例如，我们从一个 ResNet 开始，然后截断自适应池化层和之后的所有层。然后我们用我们的自定义头部替换这些层，执行生成任务。

在上一句中有很多含糊之处！我们到底如何创建一个生成图像的 CNN 头部？如果我们从一个 224 像素的输入图像开始，那么在 ResNet 主体的末尾，我们将得到一个 7×7 的卷积激活网格。我们如何将其转换为一个 224 像素的分割掩模？

当然，我们使用神经网络来做这个！所以我们需要一种能够在 CNN 中增加网格大小的层。一个简单的方法是用一个 2×2 的方块替换 7×7 网格中的每个像素。这四个像素中的每一个将具有相同的值——这被称为最近邻插值。PyTorch 为我们提供了一个可以做到这一点的层，因此一个选项是创建一个包含步长为 1 的卷积层（以及通常的批归一化和 ReLU 层）和 2×2 最近邻插值层的头部。实际上，你现在可以尝试一下！看看你是否可以创建一个设计如此的自定义头部，并在 CamVid 分割任务上尝试一下。你应该会发现你得到了一些合理的结果，尽管它们不会像我们在第一章中的结果那样好。

另一种方法是用转置卷积替换最近邻和卷积的组合，也被称为步长一半卷积。这与常规卷积相同，但首先在输入的所有像素之间插入零填充。这在图片上最容易看到——图 15-1 显示了一张来自我们在第十三章讨论过的优秀的卷积算术论文中的图表，展示了一个应用于 3×3 图像的 3×3 转置卷积。

图 15-1. 一个转置卷积（由 Vincent Dumoulin 和 Francesco Visin 提供）

正如你所看到的，结果是增加输入的大小。你现在可以通过使用 fastai 的ConvLayer类来尝试一下；在你的自定义头部中传递参数transpose=True来创建一个转置卷积，而不是一个常规卷积。

然而，这两种方法都不是很好。问题在于我们的 7×7 网格根本没有足够的信息来创建一个 224×224 像素的输出。要求每个网格单元的激活具有足够的信息来完全重建输出中的每个像素是非常困难的。

解决方案是使用跳跃连接，就像 ResNet 中那样，但是从 ResNet 主体中的激活一直跳到架构对面的转置卷积的激活。这种方法在 2015 年 Olaf Ronneberger 等人的论文“U-Net:用于生物医学图像分割的卷积网络”中有所阐述。尽管该论文侧重于医学应用，但 U-Net 已经彻底改变了各种生成视觉模型。

图 15-2。U-Net 架构（由 Olaf Ronneberger、Philipp Fischer 和 Thomas Brox 提供）

这幅图片展示了左侧的 CNN 主体（在这种情况下，它是一个常规的 CNN，而不是 ResNet，它们使用 2×2 最大池化而不是步幅为 2 的卷积，因为这篇论文是在 ResNets 出现之前写的），右侧是转置卷积（“上采样”）层。额外的跳跃连接显示为从左到右的灰色箭头（有时被称为交叉连接）。你可以看到为什么它被称为U-Net！

有了这种架构，传递给转置卷积的输入不仅是前一层中较低分辨率的网格，还有 ResNet 头部中较高分辨率的网格。这使得 U-Net 可以根据需要使用原始图像的所有信息。U-Net 的一个挑战是确切的架构取决于图像大小。fastai 有一个独特的DynamicUnet类，根据提供的数据自动生成合适大小的架构。

现在让我们专注于一个示例，其中我们利用 fastai 库编写一个自定义模型。

孪生网络

让我们回到我们在第十一章中为孪生网络设置的输入管道。你可能还记得，它由一对图像组成，标签为True或False，取决于它们是否属于同一类。

利用我们刚刚看到的内容，让我们为这个任务构建一个自定义模型并对其进行训练。如何做？我们将使用一个预训练的架构并将我们的两个图像传递给它。然后我们可以连接结果并将它们发送到一个自定义头部，该头部将返回两个预测。在模块方面，看起来像这样：

class SiameseModel(Module):
    def __init__(self, encoder, head):
        self.encoder,self.head = encoder,head

    def forward(self, x1, x2):
        ftrs = torch.cat([self.encoder(x1), self.encoder(x2)], dim=1)
        return self.head(ftrs)

要创建我们的编码器，我们只需要取一个预训练模型并切割它，就像我们之前解释的那样。函数create_body为我们执行此操作；我们只需传递我们想要切割的位置。正如我们之前看到的，根据预训练模型的元数据字典，ResNet 的切割值为-2：

encoder = create_body(resnet34, cut=-2)

然后我们可以创建我们的头部。查看编码器告诉我们最后一层有 512 个特征，所以这个头部将需要接收512*4。为什么是 4？首先我们必须乘以 2，因为我们有两个图像。然后我们需要第二次乘以 2，因为我们的连接池技巧。因此我们创建头部如下：

head = create_head(512*4, 2, ps=0.5)

有了我们的编码器和头部，我们现在可以构建我们的模型：

model = SiameseModel(encoder, head)

在使用Learner之前，我们还需要定义两件事。首先，我们必须定义要使用的损失函数。它是常规的交叉熵，但由于我们的目标是布尔值，我们需要将它们转换为整数，否则 PyTorch 会抛出错误：

def loss_func(out, targ):
    return nn.CrossEntropyLoss()(out, targ.long())

更重要的是，为了充分利用迁移学习，我们必须定义一个自定义的splitter。splitter是一个告诉 fastai 库如何将模型分成参数组的函数。这些在幕后用于在进行迁移学习时仅训练模型的头部。

这里我们想要两个参数组：一个用于编码器，一个用于头部。因此我们可以定义以下splitter（params只是一个返回给定模块的所有参数的函数）：

def siamese_splitter(model):
    return [params(model.encoder), params(model.head)]

然后，我们可以通过传递数据、模型、损失函数、分割器和任何我们想要的指标来定义我们的Learner。由于我们没有使用 fastai 的传输学习便利函数（如cnn_learner），我们必须手动调用learn.freeze。这将确保只有最后一个参数组（在本例中是头部）被训练：

learn = Learner(dls, model, loss_func=loss_func,
                splitter=siamese_splitter, metrics=accuracy)
learn.freeze()

然后我们可以直接使用通常的方法训练我们的模型：

learn.fit_one_cycle(4, 3e-3)

epoch	train_loss	valid_loss	accuracy	time
0	0.367015	0.281242	0.885656	00:26
1	0.307688	0.214721	0.915426	00:26
2	0.275221	0.170615	0.936401	00:26
3	0.223771	0.159633	0.943843	00:26

现在我们解冻并使用有区别的学习率微调整个模型一点（即，对于主体使用较低的学习率，对于头部使用较高的学习率）：

learn.unfreeze()
learn.fit_one_cycle(4, slice(1e-6,1e-4))

epoch	train_loss	valid_loss	accuracy	time
0	0.212744	0.159033	0.944520	00:35
1	0.201893	0.159615	0.942490	00:35
2	0.204606	0.152338	0.945196	00:36
3	0.213203	0.148346	0.947903	00:36

94.8％是非常好的，当我们记得以相同方式训练的分类器（没有数据增强）的错误率为 7％时。

现在我们已经看到如何创建完整的最先进的计算机视觉模型，让我们继续进行自然语言处理。

自然语言处理

将 AWD-LSTM 语言模型转换为迁移学习分类器，就像我们在第十章中所做的那样，遵循与本章第一节中的cnn_learner相似的过程。在这种情况下，我们不需要一个“元”字典，因为我们没有这么多种类的体系结构需要在主体中支持。我们只需要选择语言模型中的堆叠 RNN 作为编码器，这是一个单独的 PyTorch 模块。这个编码器将为输入的每个单词提供一个激活，因为语言模型需要为每个下一个单词输出一个预测。

要从中创建一个分类器，我们使用了ULMFiT 论文中描述的一种方法，称为“用于文本分类的 BPTT（BPT3C）”：

我们将文档分成固定长度为b的批次。在每个批次的开始，模型使用前一个批次的最终状态进行初始化；我们跟踪用于平均值和最大池化的隐藏状态；梯度被反向传播到隐藏状态对最终预测有贡献的批次。在实践中，我们使用可变长度的反向传播序列。

换句话说，分类器包含一个for循环，循环遍历每个序列的批次。状态在批次之间保持不变，并且存储每个批次的激活。最后，我们使用相同的平均值和最大连接池技巧，这与我们用于计算机视觉模型的方法相同，但这一次，我们不是在 CNN 网格单元上进行池化，而是在 RNN 序列上进行池化。

对于这个for循环，我们需要将我们的数据分批处理，但每个文本需要单独处理，因为它们各自有自己的标签。然而，这些文本很可能不会都是相同的长度，这意味着我们无法将它们都放在同一个数组中，就像我们在语言模型中所做的那样。

这就是填充将会有所帮助的地方：当获取一堆文本时，我们确定最长的文本，然后用一个特殊的标记xxpad填充较短的文本。为了避免在同一批次中有一个包含 2,000 个标记的文本和一个包含 10 个标记的文本的极端情况（因此有很多填充和浪费的计算），我们通过确保相似大小的文本被放在一起来改变随机性。文本在训练集中仍然会以某种随机顺序排列（对于验证集，我们可以简单地按长度顺序排序），但不完全是这样。

这是由 fastai 库在创建我们的DataLoaders时在幕后自动完成的。

表格

最后，让我们看看fastai.tabular模型。（我们不需要单独查看协同过滤，因为我们已经看到这些模型只是表格模型或使用点积方法，我们之前从头开始实现。）

这是TabularModel的forward方法：

if self.n_emb != 0:
    x = [e(x_cat[:,i]) for i,e in enumerate(self.embeds)]
    x = torch.cat(x, 1)
    x = self.emb_drop(x)
if self.n_cont != 0:
    x_cont = self.bn_cont(x_cont)
    x = torch.cat([x, x_cont], 1) if self.n_emb != 0 else x_cont
return self.layers(x)

我们不会在这里显示__init__，因为这并不那么有趣，但会依次查看forward中的每行代码。第一行只是测试是否有任何嵌入需要处理-如果只有连续变量，我们可以跳过这一部分：

if self.n_emb != 0:

self.embeds包含嵌入矩阵，因此这会获取每个激活

    x = [e(x_cat[:,i]) for i,e in enumerate(self.embeds)]

并将它们连接成一个单一张量：

    x = torch.cat(x, 1)

然后应用了辍学。您可以将emb_drop传递给__init__以更改此值：

    x = self.emb_drop(x)

现在我们测试是否有任何连续变量需要处理：

if self.n_cont != 0:

它们通过一个批量归一化层

    x_cont = self.bn_cont(x_cont)

并与嵌入激活连接在一起，如果有的话：

    x = torch.cat([x, x_cont], 1) if self.n_emb != 0 else x_cont

最后，这些通过线性层传递（每个线性层包括批量归一化，如果use_bn为True，并且辍学，如果ps设置为某个值或值列表）：

return self.layers(x)

恭喜！现在您已经了解了 fastai 库中使用的每个架构的所有细节！

结论

正如您所看到的，深度学习架构的细节现在不应该让您感到恐惧。您可以查看 fastai 和 PyTorch 的代码，看看发生了什么。更重要的是，尝试理解为什么会发生这种情况。查看代码中引用的论文，并尝试看看代码如何与描述的算法相匹配。

现在我们已经调查了模型的所有部分以及传递给它的数据，我们可以考虑这对于实际深度学习意味着什么。如果您拥有无限的数据，无限的内存和无限的时间，那么建议很简单：在所有数据上训练一个巨大的模型很长时间。但深度学习不简单的原因是您的数据、内存和时间通常是有限的。如果内存或时间不足，解决方案是训练一个较小的模型。如果您无法训练足够长时间以过拟合，那么您没有充分利用模型的容量。

因此，第一步是达到过拟合的点。然后问题是如何减少过拟合。图 15-3 显示了我们建议从那里优先考虑的步骤。

图 15-3。减少过拟合的步骤

许多从业者在面对过拟合模型时，从这个图表的完全错误的一端开始。他们的起点是使用更小的模型或更多的正则化。除非训练模型占用太多时间或内存，否则使用更小的模型应该是您采取的最后一步。减小模型的大小会降低模型学习数据中微妙关系的能力。

相反，您的第一步应该是寻求创建更多数据。这可能涉及向您已经拥有的数据添加更多标签，找到模型可以被要求解决的其他任务（或者，换个角度思考，识别您可以建模的不同类型的标签），或者通过使用更多或不同的数据增强技术创建额外的合成数据。由于 Mixup 和类似方法的发展，现在几乎所有类型的数据都可以获得有效的数据增强。

一旦您获得了您认为可以合理获得的尽可能多的数据，并且通过利用您可以找到的所有标签并进行所有有意义的增强来尽可能有效地使用它，如果您仍然过拟合，您应该考虑使用更具一般化能力的架构。例如，添加批量归一化可能会提高泛化能力。

如果在尽力使用数据和调整架构后仍然过拟合，您可以考虑正则化。一般来说，在最后一层或两层添加 dropout 可以很好地正则化您的模型。然而，正如我们从 AWD-LSTM 开发故事中学到的那样，在整个模型中添加不同类型的 dropout 通常会更有帮助。一般来说，具有更多正则化的较大模型更灵活，因此比具有较少正则化的较小模型更准确。

只有在考虑了所有这些选项之后，我们才建议您尝试使用较小版本的架构。

问卷

神经网络的头是什么？
神经网络的主体是什么？
什么是“剪切”神经网络？为什么我们需要在迁移学习中这样做？
model_meta是什么？尝试打印它以查看里面的内容。
阅读create_head的源代码，并确保你理解每一行的作用。
查看create_head的输出，并确保你理解每一层的存在原因，以及create_head源代码是如何创建它的。
找出如何改变create_cnn创建的 dropout、层大小和层数，并查看是否可以找到能够提高宠物识别准确性的值。
AdaptiveConcatPool2d是什么作用？
什么是最近邻插值？如何用它来上采样卷积激活？
什么是转置卷积？还有另一个名称是什么？
创建一个带有transpose=True的卷积层，并将其应用于图像。检查输出形状。
绘制 U-Net 架构。
什么是用于文本分类的 BPTT（BPT3C）？
在 BPT3C 中如何处理不同长度的序列？
尝试在笔记本中逐行运行TabularModel.forward的每一行，每个单元格一行，并查看每个步骤的输入和输出形状。
TabularModel中的self.layers是如何定义的？
预防过拟合的五个步骤是什么？
为什么在尝试其他方法预防过拟合之前不减少架构复杂性？

进一步研究

编写自己的自定义头，并尝试使用它训练宠物识别器。看看是否可以获得比 fastai 默认更好的结果。
尝试在 CNN 头部之间切换AdaptiveConcatPool2d和AdaptiveAvgPool2d，看看会有什么不同。
编写自己的自定义分割器，为每个 ResNet 块创建一个单独的参数组，以及一个单独的参数组用于干扰。尝试使用它进行训练，看看是否可以改善宠物识别器。
阅读关于生成图像模型的在线章节，并创建自己的着色器、超分辨率模型或风格转移模型。
使用最近邻插值创建一个自定义头，并用它在 CamVid 上进行分割。

第十六章：训练过程

原文：www.bookstack.cn/read/th-fastai-book/76501b0f60767008.md

译者：飞龙

协议：CC BY-NC-SA 4.0

现在你知道如何为计算机视觉、自然图像处理、表格分析和协同过滤创建最先进的架构，也知道如何快速训练它们。所以我们完成了，对吧？还没有。我们仍然需要探索一下训练过程的更多内容。

我们在第四章中解释了随机梯度下降的基础：将一个小批量数据传递给模型，用损失函数将其与目标进行比较，然后计算这个损失函数对每个权重的梯度，然后使用公式更新权重：

new_weight = weight - lr * weight.grad

我们在训练循环中从头开始实现了这个，看到 PyTorch 提供了一个简单的nn.SGD类，可以为我们的每个参数进行这个计算。在本章中，我们将构建一些更快的优化器，使用一个灵活的基础。但在训练过程中，我们可能还想要改变一些东西。对于训练循环的任何调整，我们都需要一种方法来向 SGD 的基础添加一些代码。fastai 库有一个回调系统来做到这一点，我们将教你所有相关知识。

让我们从标准的 SGD 开始建立一个基线；然后我们将介绍最常用的优化器。

建立基线

首先，我们将使用普通的 SGD 创建一个基线，并将其与 fastai 的默认优化器进行比较。我们将通过使用与第十四章中相同的get_data来获取 Imagenette：

dls = get_data(URLs.IMAGENETTE_160, 160, 128)

我们将创建一个没有预训练的 ResNet-34，并传递任何接收到的参数：

def get_learner(**kwargs):
    return cnn_learner(dls, resnet34, pretrained=False,
                    metrics=accuracy, **kwargs).to_fp16()

这是默认的 fastai 优化器，具有通常的 3e-3 学习率：

learn = get_learner()
learn.fit_one_cycle(3, 0.003)

epoch	train_loss	valid_loss	accuracy	time
0	2.571932	2.685040	0.322548	00:11
1	1.904674	1.852589	0.437452	00:11
2	1.586909	1.374908	0.594904	00:11

现在让我们尝试普通的 SGD。我们可以将opt_func（优化函数）传递给cnn_learner，以便让 fastai 使用任何优化器：

learn = get_learner(opt_func=SGD)

首先要看的是lr_find：

learn.lr_find()

(0.017378008365631102, 3.019951861915615e-07)

看起来我们需要使用比我们通常使用的更高的学习率：

learn.fit_one_cycle(3, 0.03, moms=(0,0,0))

epoch	train_loss	valid_loss	accuracy	time
0	2.969412	2.214596	0.242038	00:09
1	2.442730	1.845950	0.362548	00:09
2	2.157159	1.741143	0.408917	00:09

因为用动量加速 SGD 是一个很好的主意，fastai 在fit_one_cycle中默认执行这个操作，所以我们用moms=(0,0,0)关闭它。我们很快会讨论动量。

显然，普通的 SGD 训练速度不如我们所希望的快。所以让我们学习一些技巧来加速训练！

通用优化器

为了构建我们加速的 SGD 技巧，我们需要从一个灵活的优化器基础开始。在 fastai 之前没有任何库提供这样的基础，但在 fastai 的开发过程中，我们意识到学术文献中看到的所有优化器改进都可以使用优化器回调来处理。这些是我们可以组合、混合和匹配在优化器中构建优化器步骤的小代码片段。它们由 fastai 的轻量级Optimizer类调用。这些是我们在本书中使用的两个关键方法在Optimizer中的定义：

def zero_grad(self):
    for p,*_ in self.all_params():
        p.grad.detach_()
        p.grad.zero_()

def step(self):
    for p,pg,state,hyper in self.all_params():
        for cb in self.cbs:
            state = _update(state, cb(p, **{**state, **hyper}))
        self.state[p] = state

正如我们在从头开始训练 MNIST 模型时看到的，zero_grad只是循环遍历模型的参数并将梯度设置为零。它还调用detach_，这会删除任何梯度计算的历史，因为在zero_grad之后不再需要它。

更有趣的方法是step，它循环遍历回调（cbs）并调用它们来更新参数（如果cb返回任何内容，_update函数只是调用state.update）。正如你所看到的，Optimizer本身不执行任何 SGD 步骤。让我们看看如何将 SGD 添加到Optimizer中。

这是一个优化器回调，通过将-lr乘以梯度并将其添加到参数（当在 PyTorch 中传递Tensor.add_两个参数时，它们在相加之前相乘）来执行单个 SGD 步骤：

def sgd_cb(p, lr, **kwargs): p.data.add_(-lr, p.grad.data)

我们可以使用cbs参数将这个传递给Optimizer；我们需要使用partial，因为Learner将调用这个函数来创建我们的优化器：

opt_func = partial(Optimizer, cbs=[sgd_cb])

让我们看看这是否有效：

learn = get_learner(opt_func=opt_func)
learn.fit(3, 0.03)

epoch	train_loss	valid_loss	accuracy	time
0	2.730918	2.009971	0.332739	00:09
1	2.204893	1.747202	0.441529	00:09
2	1.875621	1.684515	0.445350	00:09

它正在工作！这就是我们如何在 fastai 中从头开始创建 SGD。现在让我们看看这个“动量”是什么。

动量

正如在第四章中所描述的，SGD 可以被看作站在山顶上，通过在每个时间点沿着最陡峭的斜坡方向迈出一步来往下走。但如果我们有一个球在山上滚动呢？在每个给定点，它不会完全按照梯度的方向前进，因为它会有动量。具有更多动量的球（例如，一个更重的球）会跳过小凸起和洞，更有可能到达崎岖山脉的底部。另一方面，乒乓球会卡在每一个小缝隙中。

那么我们如何将这个想法带到 SGD 中呢？我们可以使用移动平均值，而不仅仅是当前梯度，来进行我们的步骤：

weight.avg = beta * weight.avg + (1-beta) * weight.grad
new_weight = weight - lr * weight.avg

这里beta是我们选择的一个数字，定义了要使用多少动量。如果beta为 0，第一个方程变为weight.avg = weight.grad，因此我们最终得到普通的 SGD。但如果它接近 1，所选择的主要方向是以前步骤的平均值。（如果你对统计学有一点了解，你可能会在第一个方程中认出指数加权移动平均，它经常用于去噪数据并获得潜在趋势。）

请注意，我们写weight.avg以突出显示我们需要为模型的每个参数存储移动平均值（它们都有自己独立的移动平均值）。

图 16-1 显示了一个单参数的噪声数据示例，其中动量曲线以红色绘制，参数的梯度以蓝色绘制。梯度增加，然后减少，动量很好地跟随总体趋势，而不会受到噪声的太大影响。

图 16-1。动量的一个例子

如果损失函数有窄谷，我们需要导航：普通的 SGD 会使我们从一边反弹到另一边，而带有动量的 SGD 会将这些平均值平滑地滚动到一侧。参数beta确定我们使用的动量的强度：使用较小的beta，我们会保持接近实际梯度值，而使用较高的beta，我们将主要朝着梯度的平均值前进，直到梯度的任何变化使得该趋势移动。

使用较大的beta，我们可能会错过梯度改变方向并滚动到一个小的局部最小值。这是一个期望的副作用：直观地，当我们向模型展示一个新的输入时，它会看起来像训练集中的某个东西，但不会完全像它。它将对应于损失函数中接近我们在训练结束时得到的最小值的点，但不会在那个最小值。因此，我们宁愿在一个宽阔的最小值中进行训练，附近的点具有近似相同的损失（或者如果你喜欢的话，损失尽可能平坦的点）。图 16-2 显示了当我们改变beta时，图 16-1 中的图表如何变化。

图 16-2。不同 beta 值的动量

我们可以看到在这些示例中，beta太高会导致梯度的整体变化被忽略。在带动量的 SGD 中，通常使用的beta值为 0.9。

fit_one_cycle默认从 0.95 开始，逐渐调整到 0.85，然后在训练结束时逐渐移回到 0.95。让我们看看在普通 SGD 中添加动量后我们的训练情况如何。

要向我们的优化器添加动量，我们首先需要跟踪移动平均梯度，我们可以使用另一个回调来实现。当优化器回调返回一个dict时，它用于更新优化器的状态，并在下一步传回优化器。因此，这个回调将跟踪梯度平均值，存储在名为grad_avg的参数中：

def average_grad(p, mom, grad_avg=None, **kwargs):
    if grad_avg is None: grad_avg = torch.zeros_like(p.grad.data)
    return {'grad_avg': grad_avg*mom + p.grad.data}

要使用它，我们只需在我们的步骤函数中用grad_avg替换p.grad.data：

def momentum_step(p, lr, grad_avg, **kwargs): p.data.add_(-lr, grad_avg)

opt_func = partial(Optimizer, cbs=[average_grad,momentum_step], mom=0.9)

Learner将自动调度mom和lr，因此fit_one_cycle甚至可以与我们自定义的Optimizer一起使用：

learn = get_learner(opt_func=opt_func)
learn.fit_one_cycle(3, 0.03)

epoch	train_loss	valid_loss	accuracy	time
0	2.856000	2.493429	0.246115	00:10
1	2.504205	2.463813	0.348280	00:10
2	2.187387	1.755670	0.418853	00:10

learn.recorder.plot_sched()

我们仍然没有得到很好的结果，所以让我们看看我们还能做什么。

RMSProp

RMSProp 是由 Geoffrey Hinton 在他的 Coursera 课程“神经网络机器学习”第 6 讲 e中介绍的 SGD 的另一种变体。与 SGD 的主要区别在于它使用自适应学习率：每个参数都有自己特定的学习率，由全局学习率控制。这样，我们可以通过为需要大幅度改变的权重提供更高的学习率来加速训练，而对于已经足够好的权重，则提供较低的学习率。

我们如何决定哪些参数应该具有较高的学习率，哪些不应该？我们可以查看梯度来获取一个想法。如果一个参数的梯度一直接近于零，那么该参数将需要更高的学习率，因为损失是平的。另一方面，如果梯度到处都是，我们可能应该小心并选择一个较低的学习率以避免发散。我们不能简单地平均梯度来查看它们是否变化很多，因为大正数和大负数的平均值接近于零。相反，我们可以使用通常的技巧，即取绝对值或平方值（然后在平均后取平方根）。

再次，为了确定噪声背后的一般趋势，我们将使用移动平均值，具体来说是梯度的平方的移动平均值。然后，我们将通过使用当前梯度（用于方向）除以这个移动平均值的平方根来更新相应的权重（这样，如果它很低，有效的学习率将更高，如果它很高，有效的学习率将更低）：

w.square_avg = alpha * w.square_avg + (1-alpha) * (w.grad ** 2)
new_w = w - lr * w.grad / math.sqrt(w.square_avg + eps)

eps（epsilon）是为了数值稳定性而添加的（通常设置为 1e-8），alpha的默认值通常为 0.99。

我们可以通过做与avg_grad类似的事情将其添加到Optimizer中，但是多了一个**2：

def average_sqr_grad(p, sqr_mom, sqr_avg=None, **kwargs):
    if sqr_avg is None: sqr_avg = torch.zeros_like(p.grad.data)
    return {'sqr_avg': sqr_avg*sqr_mom + p.grad.data**2}

我们可以像以前一样定义我们的步骤函数和优化器：

def rms_prop_step(p, lr, sqr_avg, eps, grad_avg=None, **kwargs):
    denom = sqr_avg.sqrt().add_(eps)
    p.data.addcdiv_(-lr, p.grad, denom)

opt_func = partial(Optimizer, cbs=[average_sqr_grad,rms_prop_step],
                   sqr_mom=0.99, eps=1e-7)

让我们试一试：

learn = get_learner(opt_func=opt_func)
learn.fit_one_cycle(3, 0.003)

epoch	train_loss	valid_loss	accuracy	time
0	2.766912	1.845900	0.402548	00:11
1	2.194586	1.510269	0.504459	00:11
2	1.869099	1.447939	0.544968	00:11

好多了！现在我们只需将这些想法结合起来，我们就有了 Adam，fastai 的默认优化器。

Adam

Adam 将 SGD 与动量和 RMSProp 的思想结合在一起：它使用梯度的移动平均作为方向，并除以梯度平方的移动平均的平方根，为每个参数提供自适应学习率。

Adam 计算移动平均值的方式还有一个不同之处。它采用无偏移动平均值，即

w.avg = beta * w.avg + (1-beta) * w.grad
unbias_avg = w.avg / (1 - (beta**(i+1)))

如果我们是第i次迭代（从 0 开始，就像 Python 一样）。这个除数1 - (beta**(i+1))确保无偏平均值看起来更像开始时的梯度（因为beta < 1，分母很快接近 1）。

将所有内容放在一起，我们的更新步骤看起来像这样：

w.avg = beta1 * w.avg + (1-beta1) * w.grad
unbias_avg = w.avg / (1 - (beta1**(i+1)))
w.sqr_avg = beta2 * w.sqr_avg + (1-beta2) * (w.grad ** 2)
new_w = w - lr * unbias_avg / sqrt(w.sqr_avg + eps)

至于 RMSProp，eps通常设置为 1e-8，文献建议的(beta1，beta2)的默认值为(0.9，0.999)。

在 fastai 中，Adam 是我们使用的默认优化器，因为它可以加快训练速度，但我们发现beta2=0.99更适合我们使用的调度类型。beta1是动量参数，我们在调用fit_one_cycle时用参数moms指定。至于eps，fastai 使用默认值 1e-5。eps不仅仅对数值稳定性有用。更高的eps限制了调整学习率的最大值。举个极端的例子，如果eps为 1，那么调整后的学习率永远不会高于基本学习率。

与其在书中展示所有这些代码，我们让你去看看 fastai 的优化器笔记本https://oreil.ly/24_O[GitHub 存储库]（浏览 _nbs文件夹并搜索名为optimizer的笔记本）。你会看到到目前为止我们展示的所有代码，以及 Adam 和其他优化器，以及许多示例和测试。

当我们从 SGD 转换为 Adam 时，有一件事情会改变，那就是我们如何应用权重衰减，这可能会产生重要的后果。

解耦权重衰减

权重衰减，我们在第八章中讨论过，相当于（在普通 SGD 的情况下）用以下方式更新参数：

new_weight = weight - lr*weight.grad - lr*wd*weight

这个公式的最后一部分解释了这种技术的名称：每个权重都会被lr * wd的因子衰减。

权重衰减的另一个名称是L2 正则化，它包括将所有平方权重的总和添加到损失中（乘以权重衰减）。正如我们在第八章中看到的，这可以直接表达在梯度上：

weight.grad += wd*weight

对于 SGD，这两个公式是等价的。然而，这种等价性仅适用于标准 SGD，因为正如我们在动量、RMSProp 或 Adam 中看到的，更新周围有一些额外的梯度公式。

大多数库使用第二种公式，但 Ilya Loshchilov 和 Frank Hutter 在“解耦权重衰减正则化”中指出，第一种方法是 Adam 优化器或动量的唯一正确方法，这就是为什么 fastai 将其设为默认值。

现在你知道了learn.fit_one_cycle这行代码背后隐藏的一切！

然而，优化器只是训练过程的一部分。当你需要改变 fastai 的训练循环时，你不能直接改变库内的代码。相反，我们设计了一套回调系统，让你可以在独立的块中编写任何你喜欢的调整，然后进行混合和匹配。

回调

有时候你需要稍微改变事物的工作方式。事实上，我们已经看到了这种情况的例子：Mixup，fp16 训练，每个时期重置模型以训练 RNN 等。我们如何进行这种类型的调整训练过程？

我们已经看到了基本训练循环，借助Optimizer类的帮助，对于单个时期，它看起来像这样：

for xb,yb in dl:
    loss = loss_func(model(xb), yb)
    loss.backward()
    opt.step()
    opt.zero_grad()

图 16-3 展示了如何形象地描绘这一点。

图 16-3. 基本训练循环

深度学习从业者通常自定义训练循环的常规方式是复制现有训练循环，然后将特定更改所需的代码插入其中。这几乎是你在网上找到的所有代码的样子。但是它存在严重问题。

某个特定调整过的训练循环不太可能满足您的特定需求。可以对训练循环进行数百次更改，这意味着可能有数十亿种可能的排列组合。您不能只是从这里的一个训练循环中复制一个调整，从那里的另一个训练循环中复制另一个调整，然后期望它们都能一起工作。每个都将基于对其所在环境的不同假设，使用不同的命名约定，并期望数据以不同的格式存在。

我们需要一种方法，允许用户在训练循环的任何部分插入自己的代码，但以一种一致和明确定义的方式。计算机科学家已经提出了一个优雅的解决方案：回调。回调是您编写并注入到另一段代码中的代码片段，在预定义的点执行。事实上，回调已经多年用于深度学习训练循环。问题在于，在以前的库中，只能在可能需要的一小部分地方注入代码——更重要的是，回调无法执行它们需要执行的所有操作。

为了能够像手动复制和粘贴训练循环并直接插入代码一样灵活，回调必须能够读取训练循环中的所有可能信息，根据需要修改所有信息，并完全控制批次、周期甚至整个训练循环何时应该终止。fastai 是第一个提供所有这些功能的库。它修改了训练循环，使其看起来像图 16-4。

图 16-4. 带有回调的训练循环

这种方法的有效性在过去几年中得到了验证——通过使用 fastai 回调系统，我们能够实现我们尝试的每一篇新论文，并满足每一个修改训练循环的用户请求。训练循环本身并不需要修改。图 16-5 展示了添加的一些回调。

图 16-5. 一些 fastai 回调

这很重要，因为这意味着我们头脑中的任何想法，我们都可以实现。我们永远不需要深入 PyTorch 或 fastai 的源代码，并临时拼凑一个系统来尝试我们的想法。当我们实现自己的回调来开发自己的想法时，我们知道它们将与 fastai 提供的所有其他功能一起工作——因此我们将获得进度条、混合精度训练、超参数退火等等。

另一个优点是，它使逐渐删除或添加功能以及执行消融研究变得容易。您只需要调整传递给 fit 函数的回调列表。

例如，这是每个训练循环批次运行的 fastai 源代码：

try:
    self._split(b);                                  self('begin_batch')
    self.pred = self.model(*self.xb);                self('after_pred')
    self.loss = self.loss_func(self.pred, *self.yb); self('after_loss')
    if not self.training: return
    self.loss.backward();                            self('after_backward')
    self.opt.step();                                 self('after_step')
    self.opt.zero_grad()
except CancelBatchException:                         self('after_cancel_batch')
finally:                                             self('after_batch')

形式为self('...')的调用是回调被调用的地方。正如您所看到的，这发生在每一步之后。回调将接收整个训练状态，并且还可以修改它。例如，输入数据和目标标签分别在self.xb和self.yb中；回调可以修改这些以修改训练循环看到的数据。它还可以修改self.loss甚至梯度。

让我们通过编写一个回调来看看这在实践中是如何工作的。

创建回调

当您想要编写自己的回调时，可用事件的完整列表如下：

begin_fit

在做任何事情之前调用；适用于初始设置。

begin_epoch

在每个周期开始时调用；对于需要在每个周期重置的任何行为都很有用。

begin_train

在周期的训练部分开始时调用。

begin_batch

在每个批次开始时调用，就在绘制该批次之后。可以用于对批次进行任何必要的设置（如超参数调度）或在输入/目标进入模型之前对其进行更改（例如，通过应用 Mixup）。

after_pred

在计算模型对批次的输出后调用。可以用于在将其馈送到损失函数之前更改该输出。

after_loss

在计算损失之后但在反向传播之前调用。可以用于向损失添加惩罚（例如在 RNN 训练中的 AR 或 TAR）。

after_backward

在反向传播之后调用，但在参数更新之前调用。可以在更新之前对梯度进行更改（例如通过梯度裁剪）。

after_step

在步骤之后和梯度归零之前调用。

after_batch

在批次结束时调用，以在下一个批次之前执行任何必要的清理。

after_train

在时代的训练阶段结束时调用。

begin_validate

在时代的验证阶段开始时调用；用于特定于验证所需的任何设置。

after_validate

在时代的验证部分结束时调用。

after_epoch

在时代结束时调用，进行下一个时代之前的任何清理。

after_fit

在训练结束时调用，进行最终清理。

此列表的元素可作为特殊变量event的属性使用，因此您只需在笔记本中键入event.并按 Tab 键即可查看所有选项的列表

让我们看一个例子。您是否还记得在第十二章中我们需要确保在每个时代的训练和验证开始时调用我们的特殊reset方法？我们使用 fastai 提供的ModelResetter回调来为我们执行此操作。但它究竟是如何工作的呢？这是该类的完整源代码：

class ModelResetter(Callback):
    def begin_train(self):    self.model.reset()
    def begin_validate(self): self.model.reset()

是的，实际上就是这样！它只是在完成时代的训练或验证后，调用一个名为reset的方法。

回调通常像这样“简短而甜美”。实际上，让我们再看一个。这是添加 RNN 正则化（AR 和 TAR）的 fastai 回调的源代码：

class RNNRegularizer(Callback):
    def __init__(self, alpha=0., beta=0.): self.alpha,self.beta = alpha,beta

    def after_pred(self):
        self.raw_out,self.out = self.pred[1],self.pred[2]
        self.learn.pred = self.pred[0]

    def after_loss(self):
        if not self.training: return
        if self.alpha != 0.:
            self.learn.loss += self.alpha * self.out[-1].float().pow(2).mean()
        if self.beta != 0.:
            h = self.raw_out[-1]
            if len(h)>1:
                self.learn.loss += self.beta * (h[:,1:] - h[:,:-1]
                                               ).float().pow(2).mean()

自己编写代码。

回去重新阅读“激活正则化和时间激活正则化”，然后再看看这里的代码。确保您理解它在做什么以及为什么。

在这两个示例中，请注意我们如何可以通过直接检查self.model或self.pred来访问训练循环的属性。这是因为Callback将始终尝试获取其内部Learner中没有的属性。这些是self.learn.model或self.learn.pred的快捷方式。请注意，它们适用于读取属性，但不适用于编写属性，这就是为什么当RNNRegularizer更改损失或预测时，您会看到self.learn.loss =或self.learn.pred =。

在编写回调时，可以直接检查Learner的以下属性：

model

用于训练/验证的模型。

data

底层的DataLoaders。

loss_func

使用的损失函数。

opt

用于更新模型参数的优化器。

opt_func

用于创建优化器的函数。

cbs

包含所有Callback的列表。

dl

用于迭代的当前DataLoader。

x/xb

从self.dl中绘制的最后一个输入（可能由回调修改）。xb始终是一个元组（可能有一个元素），x是去元组化的。您只能分配给xb。

y/yb

从self.dl中绘制的最后一个目标（可能由回调修改）。yb始终是一个元组（可能有一个元素），y是去元组化的。您只能分配给yb。

pred

从self.model中绘制的最后预测（可能由回调修改）。

loss

最后计算的损失（可能由回调修改）。

n_epoch

此次训练的时代数。

n_iter

当前self.dl中的迭代次数。

纪元

当前纪元索引（从 0 到n_epoch-1）。

iter

self.dl中的当前迭代索引（从 0 到n_iter-1）。

以下属性由TrainEvalCallback添加，除非您刻意删除该回调，否则应该可用：

train_iter

自此次训练开始以来已完成的训练迭代次数

pct_train

已完成的训练迭代的百分比（从 0 到 1）

training

一个指示我们是否处于训练模式的标志

以下属性由Recorder添加，除非您刻意删除该回调，否则应该可用：

smooth_loss

训练损失的指数平均版本

回调也可以通过使用异常系统中断训练循环的任何部分。

回调排序和异常

有时回调需要能够告诉 fastai 跳过一个批次或一个纪元，或者完全停止训练。例如，考虑TerminateOnNaNCallback。这个方便的回调将在损失变为无穷大或NaN（不是一个数字）时自动停止训练。以下是此回调的 fastai 源代码：

class TerminateOnNaNCallback(Callback):
    run_before=Recorder
    def after_batch(self):
        if torch.isinf(self.loss) or torch.isnan(self.loss):
            raise CancelFitException

raise CancelFitException这一行告诉训练循环在这一点中断训练。训练循环捕获此异常并不再运行任何进一步的训练或验证。可用的回调控制流异常如下：

CancelFitException

跳过本批次的其余部分并转到after_batch。

CancelEpochException

跳过本纪元的训练部分的其余部分并转到after_train。

CancelTrainException

跳过本纪元的验证部分的其余部分并转到after_validate。

CancelValidException

跳过本纪元的其余部分并转到after_epoch。

CancelBatchException

训练中断并转到after_fit。

您可以检测是否发生了其中一个异常，并添加代码，以在以下事件之后立即执行：

after_cancel_batch

在继续到after_batch之前立即到达CancelBatchException后

after_cancel_train

在继续到after_epoch之前立即到达CancelTrainException后

after_cancel_valid

在继续到after_epoch之前立即到达CancelValidException后

after_cancel_epoch

在继续到after_epoch之前立即到达CancelEpochException后

after_cancel_fit

在继续到after_fit之前立即到达CancelFitException后

有时需要按特定顺序调用回调。例如，在TerminateOnNaNCallback的情况下，很重要的是Recorder在此回调之后运行其after_batch，以避免注册NaN损失。您可以在回调中指定run_before（此回调必须在之前运行…）或run_after（此回调必须在之后运行…）以确保您需要的顺序。

结论

在本章中，我们仔细研究了训练循环，探讨了 SGD 的变体以及为什么它们可能更强大。在撰写本文时，开发新的优化器是一个活跃的研究领域，因此在阅读本章时，可能会在书籍网站上发布新变体的附录。请务必查看我们的通用优化器框架如何帮助您快速实现新的优化器。

我们还研究了强大的回调系统，该系统允许您通过允许您在每个步骤之间检查和修改任何参数来自定义训练循环的每一部分。

问卷调查

SGD 一步的方程是什么，以数学或代码形式（您喜欢的方式）？
我们传递什么给cnn_learner以使用非默认优化器？
什么是优化器回调？
优化器中的zero_grad是做什么的？
优化器中的step是做什么的？通常优化器中如何实现它？
重写sgd_cb以使用+=运算符，而不是add_。
什么是动量？写出方程式。
动量的物理类比是什么？它如何应用在我们的模型训练设置中？
动量值越大对梯度有什么影响？
1cycle 训练的动量的默认值是多少？
RMSProp 是什么？写出方程。
梯度的平方值表示什么？
Adam 与动量和 RMSProp 有何不同？
写出 Adam 的方程。
计算几批虚拟值的unbias_avg和w.avg的值。
在 Adam 中，eps值较高会产生什么影响？
阅读 fastai 存储库中的优化器笔记本并执行它。
在哪些情况下，像 Adam 这样的动态学习率方法会改变权重衰减的行为？
训练循环的四个步骤是什么？
为什么使用回调比为每个想要添加的调整编写新的训练循环更好？
fastai 回调系统设计的哪些方面使其像复制和粘贴代码片段一样灵活？
在编写回调时，如何获取可用事件的列表？
编写ModelResetter回调（请不要偷看）。
如何在回调内部访问训练循环的必要属性？何时可以使用或不使用与它们配套的快捷方式？
回调如何影响训练循环的控制流？
编写TerminateOnNaN回调（如果可能的话，请不要偷看）。
如何确保你的回调在另一个回调之后或之前运行？

进一步研究

查阅“修正的 Adam”论文，使用通用优化器框架实现它，并尝试一下。搜索其他最近在实践中表现良好的优化器，并选择一个实现。
查看文档中的混合精度回调。尝试理解每个事件和代码行的作用。
从头开始实现自己版本的学习率查找器。与 fastai 的版本进行比较。
查看 fastai 附带的回调的源代码。看看能否找到一个与你要做的类似的回调，以获得一些灵感。

深度学习基础：总结

恭喜你——你已经完成了书中“深度学习基础”部分！现在你理解了 fastai 的所有应用程序和最重要的架构是如何构建的，以及训练它们的推荐方法——你拥有构建这些内容所需的所有信息。虽然你可能不需要创建自己的训练循环或批归一化层，但了解幕后发生的事情对于调试、性能分析和部署解决方案非常有帮助。

既然你现在理解了 fastai 应用的基础，一定要花时间深入研究源代码笔记本，并运行和实验它们的部分。这将让你更清楚地了解 fastai 中的所有内容是如何开发的。

在下一节中，我们将更深入地探讨：我们将探索神经网络的实际前向和后向传递是如何进行的，以及我们可以利用哪些工具来获得更好的性能。然后，我们将继续进行一个项目，将书中的所有材料汇集在一起，用它来构建一个用于解释卷积神经网络的工具。最后但并非最不重要的是，我们将从头开始构建 fastai 的Learner类。