2024牛客寒假算法基础集训营1
牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ
A.DFS搜索
思路:
直接依次遍历子串即可
代码如下:
#include
using namespace std;
#define fs first
#define sc second
#define all(x) x.begin(),x.end()
typedef long long ll;
typedef pair PII;
void solve()
{
int n;
string s;
cin>>n>>s;
string t[] = {"DFS","dfs"};
for(int i=0;i<=1;i++)
{
int k=0;
for(int j=0;j>t;
while(t--)
{
solve();
}
return 0;
} B.关鸡
思路:模拟
先考虑到最坏情况是三个,也就是答案是小于等于3的。
然后分别从左右两边遍历,遍历所有点。
1.排除(1,0)周围三个点的特殊情况,若某个点c<=0,ansl更新为1(最初设置为最大值2),同理ansr更新为2
2.再遍历符合这些条件的点相邻点是否存在(是否可以堵住这只坤),若存在则ansl or ansr置为0
3.再考虑特殊情况,用最大值3减去这3个特殊点的存在情况,更新ans
4.最后取最小值即可min(ans,ansl+ansr)
代码如下:
#include
using namespace std;
typedef pair PII;
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
set s;
int ans=3,ansl=2,ansr=2;
for(int i=0;i>r>>c;
s.insert({r,c});
if(c<=0)ansl=1;
if(c>=0)ansr=1;
}
for(auto t:s)
{
for(int i=-1;i<=1;i++)
{
int r=t.first^3,c=t.second+i;//r也可以表示为3-t.first
if(s.count({r,c}))
{
if(c<0)ansl=0;
if(c>0)ansr=0;
}
}
}
ans=ans-s.count({2,0})-s.count({1,1})-s.count({1,-1});
cout< C.按闹分配
法一:
思路:前缀和+二分
1.前缀和:计算每个人的不满意度(此外用sm统计总不满意度)
2.贪心:快排将t[ i ]小的排前面去
3.二分:找出符合条件(sm-sc<=m)的最小位置
代码如下:
#include
using namespace std;
#define fs first
#define sc second
#define all(x) x.begin(),x.end()
typedef long long ll;
typedef pair PII;
ll n,q,tc,m;
ll sm,sc;
bool check(ll x)
{
sc=sm+(n-x)*tc;
if(sc-sm<=m)return true;
return false;
}
int main()
{
cin.tie(0);cout.tie(0);
ios::sync_with_stdio(0);
cin>>n>>q>>tc;
vector t(n),sum(n+1);
for(int i=0;i>t[i];
}
sort(all(t));
ll tmp=0;
for(int i=0;i>m;
int l=0,r=n+1;
while(l>1;
if(check(mid))r=mid;
else l=mid+1;
}
ll res=0;
res=sum[l]+tc;
cout< 法二:
思路:
1.设插入下标为x
2.直接转化公式sm-sc<=m为(n-x)*tc<=m,也就是排在后面的人数n0=min(n,m/tc)//考虑到一个情况,与n取min即可
3.每次询问计算sum[n-n0]+tc即可
代码如下:
#include
using namespace std;
#define fs first
#define sc second
#define all(x) x.begin(),x.end()
typedef long long ll;
typedef pair PII;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, q, tc;
cin >> n >> q >> tc;
vector t(n);
for (int i = 0; i < n; i++) {
cin >> t[i];
}
sort(all(t));
vector sum(n + 1);
for (int i = 0; i < n; i++) {
sum[i + 1] = sum[i] + t[i];
}
while (q--) {
ll m;
cin >> m;
int n0 = min(ll(n), m / tc);
cout << sum[n - n0] + tc << '\n';
}
return 0;
} D.数组成鸡
法一:
思路:暴力枚举
先预处理出所有的数,再进行查询
1.首先考虑2^30>10^9,也就是n>=30时,需要让数组中绝对值>1的数的个数,通过若干次+1,-1下降到30以内;若n<30则不用处理
(代码中也就是判断:n-cnt[x]-cnt[x-2]<30. 因为若abs(x)可以置为1则,abs(x-2)也是1)
2.再考虑数组乘积基于[-1e9,1e9]范围,如何操作得到符合这个范围内的所有数。由于1e4.5的平方等于1e9,也就是数组但凡有两个数大于1e4.5就会溢出。所以可以通过把所有数字减去一个最小值,再让增量(+1,-1的操作)在[-1e4.5,1e4.5]之间变化(实际取大一点防止遗漏),即可得到一个上界;同理让数组减去最大值,执行相同操作得到下界。
代码如下:
#include
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
void solve()
{
int n, m; cin >> n >> m;
vectora(n);//保存数组
mapcnt;//记录每个数出现的次数
setans;//保存答案,去重
ans.insert(0);//答案至少有一个0
for(int i = 0; i < n; i ++){
cin >> a[i];
cnt[a[i]] += 1;
}
if(n >= 30){
//一定要减少绝对值不等于1的数字个数。
for(auto [x, y]: cnt){
if(n - cnt[x] - cnt[x - 2] > 30)
continue;
int mul = 1;
bool flag = true;
for(int i = 0; i < n; i ++){
mul = mul * (a[i] - (x - 1));
if(abs(mul) > 1e9){
flag = false;
break;
}
}
if(flag)
ans.insert(mul);
mul = 1, flag = true;
for(int i = 0; i < n; i ++){
mul = mul * (a[i] - (x + 1));
if(abs(mul) > 1e9){
flag = false;
break;
}
}
if(flag)
ans.insert(mul);
}
}else{
//如果n <= 30
sort(a.begin(), a.end());
int tmp = a[0];
for(int i = 0; i < n; i ++){
a[i] -= tmp;
}
for(int i = -1e6; i <= 1e6; i ++){
int mul = 1;
bool flag = true;
for(int j = 0; j < n; j ++){
mul = mul * (a[j] + i);
if(abs(mul) > 1e9){
flag = false;
break;
}
}
if(flag)
ans.insert(mul);
}
reverse(a.begin(), a.end());
tmp = a[0];
for(int i = 0; i < n; i ++){
a[i] -= tmp;
}
for(int i = -1e6; i <= 1e6; i ++){
int mul = 1;
bool flag = true;
for(int j = 0; j < n; j ++){
mul = mul * (a[j] + i);
if(abs(mul) > 1e9){
flag = false;
break;
}
}
if(flag)
ans.insert(mul);
}
}
while(m--){
int x; cin >> x;
if(ans.count(x)){
cout << "Yes" << endl;
}else{
cout << "No" << endl;
}
}
}
signed main()
{
cin.tie(0);cout.tie(0);
ios::sync_with_stdio(0);
solve();
}
(代码来自2024牛客寒假算法基础集训营1(视频讲解全部题目)-CSDN博客)
法二:
思路:
由于20!已经大于1e9了,所以我们可以考虑用20个不同的数,这个条件来判断是否纳入集合。([ -10,10 ]是最小20个不同的数,乘积为1e10)
1.sort排序,unique去重
2.再依次遍历每个数在[-1e5,1e5]范围内计算判断即可(快速幂)
代码如下:
#include "bits/stdc++.h"
#define range(a) begin(a), end(a)
using namespace std;
using i64 = long long;
constexpr int K = 1e5;
constexpr int inf = 1e9 + 1;
int power(int a, int b) {
int res = 1;
for (; b; b >>= 1) {
if (b & 1) {
if (abs(i64(res) * a) > inf) {
return inf;
}
res *= a;
}
if (abs(i64(a) * a) > inf) {
a = inf;
}
a *= a;
}
return res;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, q;
cin >> n >> q;
vector a(n);
map cnt;
for (int i = 0; i < n; i++) {
cin >> a[i];
cnt[a[i]]++;
}
sort(range(a));
a.erase(unique(range(a)), a.end());
int N = a.size();
set s{0};
if (N <= 20) {
for (int i = 0; i < N; i++) {
for (int k = -K - a[i]; k <= K - a[i]; k++) {
int res = 1;
for (int j = 0; j < N; j++) {
int x = a[j] + k, y = cnt[a[j]];
int v = power(x, y);
if (abs(i64(res) * v) > inf) {
res = inf;
break;
}
res *= v;
}
if (abs(res) < inf) {
s.insert(res);
}
}
}
}
while (q--) {
int m;
cin >> m;
cout << (s.count(m) ? "Yes" : "No") << '\n';
}
return 0;
} (代码来自【题解】2024牛客寒假算法基础集训营1_ICPC/CCPC/NOIP/NOI刷题训练题单_牛客竞赛OJ)
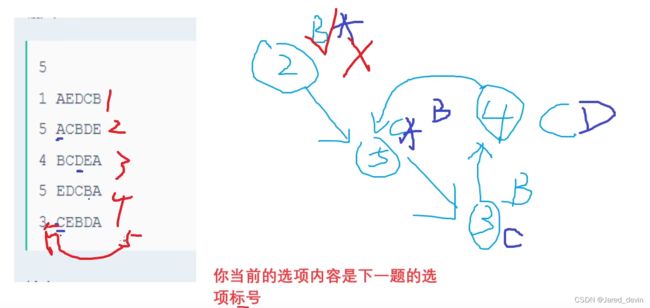
E.本题又主要考察了贪心(诈骗
思路:DFS
枚举所有比赛状况即可
代码如下:
#include
using namespace std;
#define fs first
#define sc second
#define all(x) x.begin(),x.end()
typedef long long ll;
typedef pair PII;
const int N = 15;
int a[N];
PII b[N];
int t,n,m,res;
void dfs(int u)
{
if(u==m+1)//m场比赛完毕
{
int t=1;
for(int i=1;i<=n;i++)
{
if(a[i]>a[1]) t++;
}
res=min(res,t);
return;
}
int x=b[u].first,y=b[u].second;
//x号选手赢
a[x]+=3;
dfs(u+1);
a[x]-=3;
//y号选手赢
a[y]+=3;
dfs(u+1);
a[y]-=3;
//平局
a[x]+=1;
a[y]+=1;
dfs(u+1);
a[x]-=1;
a[y]-=1;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--)
{
res=15;//最终名次
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;
b[i]={x,y};
}
dfs(1);
cout< F:鸡数题(待补
思路:第二类斯特林数
问题转变为
n 个不同的小球放在
m 个相同的箱子里,求方案数
条件1代表盒子不空
至于为什么是无区别盒子,是因为有条件2的存在。如果是有区别盒子则不用除以m的阶乘
代码如下:
#include "bits/stdc++.h"
using namespace std;
const int mod = 1e9 + 7, N = 1e5 + 10;
typedef long long ll;
ll c[N], invc[N];
ll power(ll base, ll pow) {
ll res = 1;
while (pow)
{
if(pow & 1)
res = base * res % mod;
pow >>= 1;
base = base * base % mod;
}
return res;
}
ll inv(ll x) {return power(x, mod - 2);}
void init()
{
//求阶乘
c[0] = 1;
for (int i = 1; i < N; i++) c[i] = c[i - 1] * i % mod;
//求最大阶乘的逆元
invc[N - 1] = inv(c[N - 1]);
//求每一个的逆元
for (int i = N - 2; i >= 0; i--) invc[i] = invc[i + 1] * (i + 1) % mod;
}
//求组合数
ll C(int n, int m)
{
if (m < 0 || m > n || n < 0) return 0;
return c[n] * invc[m] % mod * invc[n - m] % mod;
}
int main() {
ios::sync_with_stdio(false);
int n, m;
cin >> n >> m;
init();//预处理
ll ans = 0;
//第二类stirling数
for (int k = 0; k <= m; k++) {
if (k % 2 == 0)
ans = (ans + C(m, k) * power(m - k, n) % mod) % mod;
else
ans = (ans - C(m, k) * power(m - k, n) % mod + mod) % mod;
}
cout << ans * invc[m] % mod << '\n';
return 0;
}G.why买外卖
思路:贪心+前缀和
对优惠卷升序排序,若sum[ i +1 ] + m(当前原价) >= t[ i ].first(当前优惠卷的卷面),则更新答案ans = sum[ i +1 ] + m
代码如下:
#include
using namespace std;
typedef pair PII;
const int N = 1e5+10;
int main()
{
int t;
cin>>t;
while(t--)
{
int n,m;
cin>>n>>m;
PII t[N];
long long int sum[N];
for(int i=0;i>a>>b;
t[i]={a,b};
}
sort(t,t+n);
for(int i=0;i=t[i].first))
{
ans=m+sum[i+1];
}
}
cout< H.01背包,但是bit
法一:枚举
思路:
考虑二进制,有点像数位dp
本题考虑集合划分,累加最大值即可
![]()
代码如下:
#include
using namespace std;
void solve()
{
int n, m; cin >> n >> m;
vectorv(n), w(n);
for(int i = 0; i < n; i ++){
cin >> v[i] >> w[i];
}
int ans = 0, pre = 0;
for(int i = 31; i >= 0; i --){
int x = pre;//置为前缀
if((m >> i) & 1){
x += (1 << i) - 1;//不选这一位是1,贪心出最大情况
pre += (1 << i);//更新前缀
}
int sum = 0;
for(int j = 0; j < n; j ++){
if((x | w[j]) == x){
sum += v[j];
}
}
ans = max(ans, sum);
}
//补上x==m这种情况
int sum = 0;
for(int j = 0; j < n; j ++){
if((m | w[j]) == m){
sum += v[j];
}
}
ans = max(ans, sum);
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
//t = 1;
cin >> t;
while(t--)
solve();
}
法二:枚举
思路:
先考虑,若所选所有的物品通过或运算不大于m,也就是所选物品属于m的子集
get(int x)函数通过&运算可以找出哪些物品是x的子集(x是m每次减去最后一位1的值),获取当前价值,取max即可
代码如下:
#include
using namespace std;
#define fs first
#define sc second
#define all(x) x.begin(),x.end()
typedef long long ll;
typedef pair PII;
void solve()
{
int n,m;
cin>>n>>m;
vector v(n), w(n);
for (int i = 0; i < n; i++) {
cin >> v[i] >> w[i];
}
auto get = [&](int x) //lambda函数方便,不用传参
{
ll res = 0;
for (int i = 0; i < n; i++) {
if ((x & w[i]) == w[i]) {
res += v[i];
}
}
return res;
};
ll ans=get(m);
for(int i=m;i;i-=i&-i)//lowbit
{
ans=max(ans,get(i-1));
}
cout<>t;
while(t--)
{
solve();
}
return 0;
} I.It's bertrand paradox. Again!
思路:概率统计
发现bit-noob和buaa-noob方法的区别就是,bit生成的圆是均匀的,等概率的;而buaa的圆会更加靠近圆心(0,0),以此选择一段范围来比较概率即可。
代码如下:
#include
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
int ans = 0;
for (int i = 0; i < n; i++) {
int x, y, r;
cin >> x >> y >> r;
if (x <= 9 && x >= -9 && y <= 9 && y >= -9) {
ans++;
}
}
if (ans <= n / 100) //(19/199)^2
{
cout << "bit-noob\n";
} else {
cout << "buaa-noob\n";
}
return 0;
} J.又鸟之亦心
思路:
K.牛镇公务员考试
思路:并查集+dfs
代码如下:
#include
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int N = 1e5 + 10;
const int mod = 998244353;
int nex[N];
string choice[N];
int p[N], in[N];
bool st[N];
char t[N];
set root;
int nums;
int find(int x){
if(x != p[x])
p[x] = find(p[x]);
return p[x];
}
void init(int x){
for(int i = 1; i <= x; i ++){
p[i] = i;
root.insert(i);
}
}
void merge(int x, int y){
int px = find(x);
int py = find(y);
if(px != py){
if(in[px])
{
p[px] = py;
root.erase(px);
}
else
{
p[py] = px;
root.erase(py);
}
}
}
void dfs(int u, char answer){
if(st[nex[u]]){
if(answer == t[nex[u]]){
nums ++;
}
return;
}
char nex_answer = choice[nex[u]][answer - 'A'];
t[nex[u]] = answer;
st[nex[u]] = true;
dfs(nex[u], nex_answer);
st[nex[u]] = false;
}
void solve()
{
int n; cin >> n;
init(n);
for(int i = 1; i <= n; i ++){
int x; string s;
cin >> x >> s;
choice[i] = s;
nex[i] = x;
in[x] ++;
merge(x, i);
}
int ans = 1;
for(auto x: root){
for(int i = 0; i < 5; i ++){
t[x] = ('A' + i);
st[x] = true;
dfs(x, choice[x][i]);
}
ans = nums * ans % mod;
nums = 0;
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t = 1;
// cin >> t;
while(t--)
solve();
}
L.要有光
思路:
看俯视图,找到临界点即可

代码如下:
#include
using namespace std;
void solve() {
int c, d, h, w;
cin >> c >> d >> h >> w;
cout << 3LL * w * c << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
} M.牛客老粉才知道的秘密
思路:
画几个图找规律即可
代码如下:
#include
using namespace std;
typedef long long ll;
typedef pair PII;
void solve()
{
int n;
cin>>n;
while(n--)
{
int a;
cin>>a;
if(a%6)cout<<(a/6)*2<