数据结构1.0(基础)
近java的介绍,
文章目录
- 第一章、数据结构
-
- 1、数据结构 ?
- 2、常用的数据结构
- 数据结构? 逻辑结构and物理结构
- 第二章、数据结构基本介绍
-
- 2.1、数组(Array)
- 2.2、堆栈(Stack)
- 2.3、队列(Queue)
- 2.4、链表(Linked List)
- 2.5、树(Tree)
- 2.6、散列表(Hash table)哈希表
- 2.7、堆, 堆积(Heap)
- 2.8、图(Graph)
- 参考文章
参考 维基百科 and 菜鸟教程 等
第一章、数据结构
1、数据结构 ?
在计算机科学中,数据结构(英语:data structure)是计算机中存储、组织数据的方式。
数据结构是一种具有一定逻辑关系,在计算机中应用某种存储结构,并且封装了相应操作的数据元素集合。它包含三方面的内容,逻辑关系、存储关系及操作。
数据结构可透过编程语言所提供的数据类型、引用及其他操作加以实现。一个设计良好的数据结构,应该在尽可能使用较少的时间与空间资源的前提下,支持各种程序执行。
不同种类的数据结构适合不同种类的应用,部分数据结构甚至是为了解决特定问题而设计出来的。例如B树即为加快树状结构访问速度而设计的数据结构,常被应用在数据库和文件系统上。
正确的数据结构选择可以提高算法的效率(请参考算法效率)。在计算机程序设计的过程中,选择适当的数据结构是一项重要工作。许多大型系统的编写经验显示,程序设计的困难程度与最终成果的质量与表现,取决于是否选择了最适合的数据结构。
因为数据结构概念的普及,现代编程语言及其API中都包含了多种默认的数据结构,例如 C++ 标准模板库中的容器、Java集合框架以及微软的.NET Framework。
2、常用的数据结构
数据结构? 逻辑结构and物理结构
第二章、数据结构基本介绍
2.1、数组(Array)
在计算机科学中,数组数据结构(英语:array data structure),简称数组(英语:Array),是由相同类型的元素(element)的集合所组成的数据结构,分配一块连续的内存来存储。利用元素的索引(index)可以计算出该元素对应的存储地址。
- 数组(Array)是是最常用的数据结构, 数组的特点是长度固定, 数组的大小固定后就无法扩容了 , 数组只能存储一种类型的数据 ,
- 在内存中有空间连续性的表现,中间不会存在其他程序需要调用的数据,为此数组的专用内存空间;
- 在旧式编程语言中(如有中端语言之称的C),程序不会对数组的操作做下界判断,也就有潜在的越界操作的风险(比如会把数据写在运行中程序需要调用的核心部分的内存上)。
- 因为简单数组强烈倚赖电脑硬件之内存,所以不适用于现代的程序设计。欲使用可变大小、硬件无关性的数据类型,Java等程序设计语言均提供了更高级的数据结构:ArrayList、Vector等动态数组。
添加,删除的操作慢,因为要移动其他的元素,查询快(知道下标为前提)
其他数据结构,比如栈和队列都是由数组衍生出来的。
每一个数组元素的位置由数字编号,称为下标或者索引(index)。大多数编程语言的数组第一个元素的下标是 0
根据维度区分,有 2 种不同的数组: 一维数组 ,多维数组(数组的元素为数组)
历史
第一台数字计算机使用机器语言编程来设置和访问资料表,向量和矩阵计算的数组结构,以及许多其它目的。1945年,在建立第一个范纽曼型架构计算机时,约翰·冯·诺伊曼(John
vonNeumann)写了第一个数组排序程序(合并排序)。数组索引最初是通过自修改代码,后来使用索引寄存器和间接寻址来完成的。1960年代设计的一些主机,如Burroughs B5000及其后继者,使用存储器分段来执行硬件中的索引边界检查。
2.2、堆栈(Stack)
像放盘子一样
堆栈(英语:stack)又称为栈或堆叠,是计算机科学中的一种抽象资料类型,只允许在有序的线性资料集合的一端(称为堆栈顶端,英语:top)进行加入数据(英语:push)和移除数据(英语:pop)的运算。因而按照后进先出(LIFO, Last In First Out)的原理运作。
是一种基于先进后出(FILO)的数据结构,是一种只能在一端进行插入和删除操 作的特殊线性表。它按照先进后出的原则存储数据,先进入的数据被压入栈底,最后的数据 在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。
撤回,即 Ctrl+Z,是我们最常见的操作之一,大多数应用都会支持这个功能。
你知道它是怎么实现的吗?
答案是这样的:把之前的应用状态(限制 个数)保存到内存中,最近的状态放到第一个。这时,我们需要栈(stack)来实现这个功能。 栈中的元素采用 LIFO (Last In First Out),即后进先出。 下图的栈有 3 个元素,3 在最上面,因此它会被第一个移除:

By Vectorization: Alhadis - Own work based on: Lifo stack.png by Maxtremus, CC0, https://commons.wikimedia.org/w/index.php?curid=115938639
堆栈使用两种基本操作:推入(压栈,push)和弹出(弹栈,pop):
推入:将资料放入堆栈顶端,堆栈顶端移到新放入的资料。
弹出:将堆栈顶端资料移除,堆栈顶端移到移除后的下一笔资料。
java中对栈的一些操作
Push— 在栈的最上方插入元素
Pop— 返回栈最上方的元素,并将其删除
isEmpty— 查询栈是否为空
Top— 返回栈最上方的元素,并不删除
历史
Stacks 于 1946 年进入计算机科学文献,当时艾伦·图灵使用术语“bury”和“unbury”作为调用子例程和从子例程返回的方法。[2] [3] 子例程和两级堆栈已于1945 年在Konrad Zuse的Z4中实现。[4] [5]
慕尼黑工业大学的Klaus Samelson和Friedrich L. Bauer于 1955 年提出了称为Operationskeller(“操作地窖”)的堆栈的想法[6] [7],并于 1957 年申请了专利。 [8] [9] [10] [ 11] 1988 年 3 月,萨梅尔森去世,鲍尔因发明堆栈原理而获得IEEE计算机先锋奖。[12] [7] Charles Leonard Hamblin在 1954 年上半年[13] [7]以及Wilhelm Kämmerer [ de ]在 1958 年通过他的automatisches Gedächtnis(“自动记忆”)独立开发了类似的概念。 [14] [15] [7]
- 图灵,艾伦·马西森(1946-03-19) [1945]。自动计算引擎 (ACE) 数学部门的开发提案。(注:1946 年 3 月 19 日提交给英国国家物理实验室执行委员会。)
- 卡彭特,布莱恩·爱德华;罗伯特·威廉·多兰(1977-01-01) [1975 年 10 月]。“另一个图灵机”。计算机杂志。20(3):269-279。DOI:10.1093/comjnl/20.3.269。(11页)
- Blaauw,格里特·安妮;小布鲁克斯、弗雷德里克·菲利普斯(1997)。计算机体系结构:概念和演变。美国马萨诸塞州波士顿:Addison-Wesley Longman Publishing Co., Inc.
- 查尔斯·埃里克·拉福雷斯特(2007 年 4 月)。“2.1 Lukasiewicz 和第一代:2.1.2 德国:Konrad Zuse (1910–1995);2.2 第一代堆栈计算机:2.2.1 Zuse Z4”。第二代堆栈计算机体系结构(PDF)(论文)。加拿大滑铁卢:滑铁卢大学。第 8, 11 页。原始存档于 2022-01-20 (PDF) 。检索日期:2022 年 7 月 2 日。 (178页)
- 克劳斯·萨梅尔森(1957) [1955]。写于德国德累斯顿 Internationales Kolloquium über Probleme der Rechentechnik。Probleme der Programmierungstechnik(德语)。德国柏林:VEB Deutscher Verlag der Wissenschaften。第 61–68 页。(注意。这篇论文于 1955 年首次提出。它描述了一个数字堆栈(Zahlenkeller),但将其命名为线性辅助存储器(Linearer Hilfsspeicher)。)
- Fothe,迈克尔;威尔克,托马斯,编辑。(2015)[2014-11-14]。写于德国耶拿。Keller,Stack und automatisches Gedächtnis – eine Struktur mit Potenzial [地窖、堆栈和自动内存 - 具有潜力的结构] (PDF)(Tagungsband zum Kolloquium 14. 2014 年 11 月,耶拿)。GI 系列:信息学讲义 (LNI) – 主题(德语)。卷。T-7。德国波恩:Gesellschaft für Informatik (GI) / Köllen Druck + Verlag GmbH。国际标准书号 978-3-88579-426-4。ISSN 1614-3213。原始存档于 2020-04-12 (PDF) 。检索于2020 年 4 月 12 日。 [1](77页)
- 弗里德里希·路德维希·鲍尔;克劳斯·萨梅尔森(1957-03-30)。“Verfahren zur automatischen Verarbeitung von kodierten Daten und Rechenmaschine zur Ausübung des Verfahrens”(德语)。德国慕尼黑:德国专利局。DE-PS 1094019 。检索于2010 年 10 月 1 日。
- 弗里德里希·路德维希·鲍尔;格哈德·古斯(德语)(1982)。Informatik – Eine einführende Übersicht(德语)。卷。第 1 部分(第 3 版)。柏林:施普林格出版社。p。222.国际标准书号 3-540-11722-9。Die Bezeichnung ‘Keller’ hierfür wurde von Bauer und Samelson in einer deutschen Patentanmeldung vom 30. März 1957 eingeführt。
- 克劳斯·萨梅尔森;弗里德里希·路德维希·鲍尔(1959)。“Sequentielle Formelübersetzung”[顺序公式翻译]。Elektronische Rechenanlagen(德语)。1(4):176-182。
- 克劳斯·萨梅尔森;弗里德里希·路德维希·鲍尔(1960)。《顺序公式翻译》。ACM 的通讯。3(2):76-83。号码:10.1145/366959.366968。S2CID 16646147。
- “IEEE-计算机先锋奖 – Bauer, Friedrich L.” 慕尼黑工业大学计算机科学学院。1989年1月1日。原文存档于2017-11-07。
- 查尔斯·伦纳德·汉布林(1957 年 5 月)。基于数学符号的无地址编码方案(PDF)(打字稿)。新南威尔士理工大学。第 121-1–121-12 页。原始存档于 2020-04-12 (PDF) 。检索于2020 年 4 月 12 日。 (12页)
- Kämmerer, Wilhelm [德语] (1958-12-11)。Ziffern-Rechenautomat mit Programmierung nach mathematischem Formelbild(资格论文)(德语)。德国耶拿:数学自然科学学院,弗里德里希席勒大学。瓮:nbn:de:gbv:27-20130731-133019-7。PPN:756275237。原始存档于2023-10-14 。检索日期:2023 年 10 月 14 日。 [2](2+69页)
- Kämmerer, Wilhelm [德语] (1960)。自动化设备。Elektronisches Rechnen und Regeln(德文)。卷。1. 德国柏林:Akademie-Verlag。
2.3、队列(Queue)
队列,又称为伫列(queue),计算机科学中的一种抽象资料型别,是先进先出(FIFO, First-In-First-Out)的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端(称为rear)进行插入操作,在前端(称为front)进行删除操作。
队列的操作方式和堆栈类似,都是采用线性结构存储数据,唯一的区别在于队列只允许新数据在后端进行添加。
下图展示了一个队列,1 是最上面的元素,它会被第一个移除:
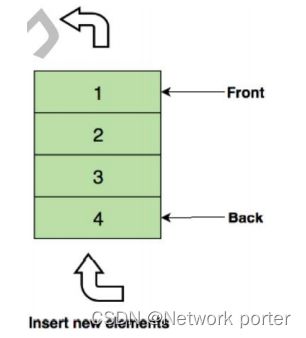
单例队列
单链队列使用链表作为基本数据结构,所以不存在伪溢出的问题,队列长度也没有限制。但插入和读取的时间代价较高
循环队列
循环队列可以更简单防止伪溢出的发生,但队列大小是固定的。
阵列队列
Enqueue— 在队列末尾插入元素
Dequeue— 将队列第一个元素删除
isEmpty— 查询队列是否为空
Top— 返回队列的第一个元素
2.4、链表(Linked List)
在计算机科学中,链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而顺序表相应的时间复杂度分别是O(logn)和O(1)。
使用链表结构可以
克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。链表最明显的好处就是,常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序,数据的存取往往要在不同的排列顺序中转换。链表允许插入和移除表上任意位置上的节点,但是不允许随机存取。
链表类型
-
循环链表
-
块状链表
块状链表本身是一个链表,但是链表储存的并不是一般的数据,而是由这些数据组成的顺序表。每一个块状链表的节点,也就是顺序表,可以被叫做一个块。图片来源 OI WIKI网站 仅供参考

-
危险操作"异或链表"
维基百科(仅供参考)
链表存储方式有
共用存储(链表的节点和其它的数据共用存储空间)
和节点
独立存储空间存储
一个链表或者多个链表使用独立的存储空间,一般用数组或者类似结构实现,优点是可以自动获得一个附加数据:唯一的编号,并且方便调试;缺点是不能动态的分配内存。当然,另外的在上面加一层块状链表用来分配内存也是可以的,这样就解决了这个问题。这种方法有时候被叫做数组模拟链表,但是事实上只是用表示在数组中的位置的下标索引代替了指向内存地址的指针,这种下标索引其实也是逻辑上的指针,整个结构还是链表,并不算是被模拟的(但是可以说成是用数组实现的链表)。
堆栈,队列 就是链表构建的
链表开发于1955年至1956年,由当时所属于兰德公司的艾伦·纽厄尔、克里夫·肖和司马贺在他们编写的信息处理语言(IPL)中做为原始数据类型所编写。IPL被作者们用来开发几种早期的人工智能程序,包括逻辑推理机,通用问题解算器和一个计算机象棋程序。
2.5、树(Tree)
树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
TREE分类
有序/无序
-
有序树/搜索树/查找树:树中任意节点的子节点之间有顺序关系,这种树称为有序树。即树的所有节点按照一定的顺序排列,这样进行插入、删除、查找时效率就会非常高
-
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树。
平衡/不平衡
- 平衡树
-
- 绝对平衡:所有叶节点在同一层
-
- 非绝对平衡
- 不平衡树
节点分叉情况
- 等叉树: 是每个节点的键值个数都相同、子节点个数也都相同。
-
- 二叉树: 每个节点最多包含有两个子树的树为二叉树。
-
-
- 完全二叉树: 对于一棵二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
-
-
-
-
- 满二叉树: 所有叶节点都在最底层的完全二叉树;
-
-
-
-
- 平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
-
-
-
- 排序二叉树(二叉查找树(英语:Binary Search Tree)):也称二叉搜索树、有序二叉树;
-
-
- 霍夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;
-
- 多叉树
- 不等叉树: 每个节点的键值个数不一定相同、子节点个数也不一定相同
-
- B树:对不等叉树的节点键值数和插入、删除逻辑添加一些特殊的要求,使其能达到绝对平衡的效果。B树全称Balance Tree。如果某个B树上所有节点的分叉数最大值是m,则把这个B数叫做m阶B树。(B树有很多种)
2.6、散列表(Hash table)哈希表
根据键(Key)而直接访问在存储器存储位置的数据结构。也就是说,它通过计算出一个键值的函数,将所需查询的数据映射到表中一个位置来让人访问,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表。
基本概念
- 若关键字为k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接获取所查记录。称这个对应关系f为散列函数,按这个思想建立的表为散列表。
- 对不同的关键字可能得到同一散列地址,即

这种现象称为冲突(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数f(k)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。 - 若对于关键字集合中的任一个关键字,经散列函数镜像到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
效率
散列表的查找过程基本上和造表过程相同。一些关键码可通过散列函数转换的地址直接找到,另一些关键码在散列函数得到的地址上产生了冲突,需要按处理冲突的方法进行查找。在介绍的三种处理冲突的方法中,产生冲突后的查找仍然是给定值与关键码进行比较的过程。所以,对散列表查找效率的量度,依然用平均查找长度来衡量。
查找过程中,关键码的比较次数,取决于产生冲突的多少,产生的冲突少,查找效率就高,产生的冲突多,查找效率就低。因此,影响产生冲突多少的因素,也就是影响查找效率的因素。影响产生冲突多少有以下三个因素:
- 散列函数是否均匀;
- 处理冲突的方法;
- 散列表的载荷因子(英语:load factor)。
载荷因子
散列表的载荷因子定义为:
α = 填入表中的元素个数 / 散列表的长度
α是散列表装满程度的标志因子。由于表长是定值,
α 与“填入表中的元素个数”成正比,所以,
α 越大,表明填入表中的元素越多,产生冲突的可能性就越大;反之,
α越小,标明填入表中的元素越少,产生冲突的可能性就越小。
实际上,散列表的平均查找长度是载荷因子α的函数,只是不同处理冲突的方法有不同的函数。
2.7、堆, 堆积(Heap)
堆(Heap)是计算机科学中的一种特别的完全二叉树。
若是满足以下特性,即可称为堆:“给定堆中任意节点P和C,若P是C的母节点,那么P的值会小于等于(或大于等于)C的值”。若母节点的值恒小于等于子节点的值,此堆称为最小堆(minheap);
反之,若母节点的值恒大于等于子节点的值,此堆称为最大堆(max heap)。在堆中最顶端的那一个节点,称作根节点(root node),根节点本身没有母节点(parent node)。
堆排序是由JWJ Williams于
1964 年发明的。 该论文还介绍了二叉堆本身就是一种有用的数据结构。[5]同年,Robert W.
Floyd发布了一个改进版本,可以就地对数组进行排序,继续他早期对树排序算法的研究。
性质
堆的实现通过构造二叉堆(binary heap),实为二叉树的一种;由于其应用的普遍性,当不加限定时,均指该数据结构的这种实现。这种数据结构具有以下性质。
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
2.8、图(Graph)
图的存储和想象的不一样,更像是组合出来的一个列阵我理解的
在计算机科学中,图(英语:graph)是一种抽象数据类型,用于实现数学中图论的无向图和有向图的概念。
一般的图由节点(也称为顶点)和连接这些节点的边(也称为弧)组成
图的数据结构包含一个有限(可能是可变的)的集合作为节点集合,以及一个无序对(对应无向图)或有序对(对应有向图)的集合作为边(有向图中也称作弧)的集合。节点可以是图结构的一部分,也可以是用整数下标或引用表示的外部实体。
分类
有向图和无向图 有方向的就是有向图,没有就是无向,还有多重图,权重图等等
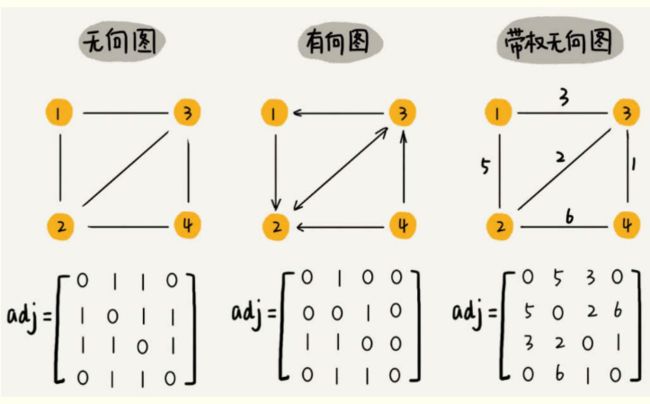
图片来自:数据结构与算法(十一)——图(Graph)
权重分类
- 无权图(Unweighted Graph):图中的边不具有任何权重值,仅表示两个顶点之间存在连接。
- 权重图(Weighted Graph):图中的每条边都有一个关联的权重值,这个权重值可以代表距离、成本或其他相关度量
图的数据结构还可能包含和每条边相关联的数值(edge value),例如一个标号或一个数值(即权重,weight;表示花费、容量、长度等)。
结构
-
领接表
节点存储为记录或对象,且为每个节点创建一个列表。这些列表可以按节点存储其余的信息;
是表示了图中与每一个顶点相邻的边集的集合,这里的集合指的是无序集。。。。

-
邻接矩阵
一个二维矩阵,其中行与列分别表示边的起点和终点。顶点上的值存储在外部。矩阵中可以存储边的值。 -
关联矩阵
一个二维矩阵,行表示顶点,列表示边。矩阵中的数值用于标识顶点和边的关系(是起点、是终点、不在这条边上等)。
用处
对于复杂的数据结构操作,如搜索、遍历(DFS/BFS)、最短路径算法(Dijkstra、Bellman-Ford、Floyd-Warshall
等)以及最小生成树算法(Prim、Kruskal 等),都需要深入理解和掌握图这种数据结构
参考文章
个人笔记,不同意见,望有交流
直接可以点击跳转连接
作者 维基百科
作者:xeh的学习笔记
阿里:通灵义码


