Rust 数据结构与算法:5栈:用栈实现前缀、中缀、后缀表达式
3、前缀、中缀和后缀表达式
计算机是从左到右处理数据的,类似(A + (B * C))这样的完全括号表达式,计算机如何跳到内部括号计算乘法,然后跳到外部括号计算加法呢?
一种直观的方法是将运算符移到操作数外,分离运算符和操作数。计算时先取运算符再取操作数,计算结果则作为当前值参与后面的运算,直到完成对整个表达式的计算。
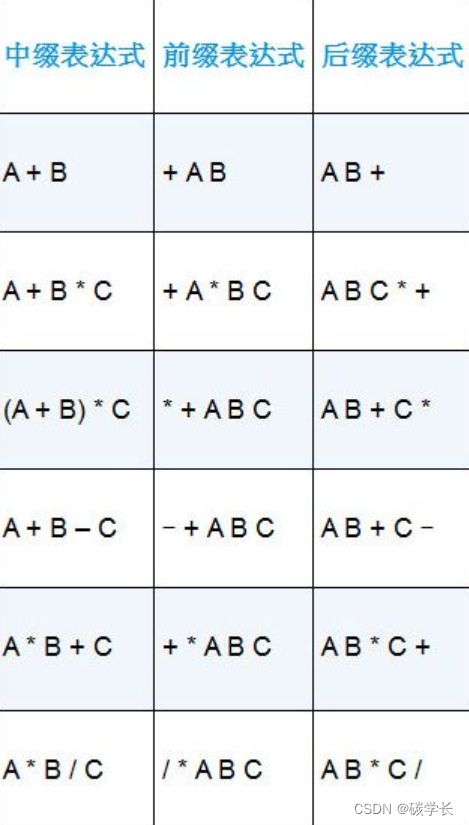
可将中缀表达式A + B中的“+”移出来,既可以放前面,也可以放后面,得到的将是+ A B和A B +。这两种不同的表达式分别被称为前缀表达式和后缀表达式。
前缀表达式要求所有运算符在处理的两个操作数之前,后缀表达式则要求所有运算符在相应的操作数之后。
这里规定:运算符只有+ - * /,操作数则被定义为任何大写字母A~Z或数字0~9。
代码如下:
#[derive(Debug)]
struct Stack<T> {
size: usize, // 栈大小
data: Vec<T>, // 栈数据
}
impl<T> Stack<T> {
// 初始化空栈
fn new() -> Self {
Self {
size: 0,
data: Vec::new(), // 以 Vec 为低层
}
}
fn is_empty(&self) -> bool {
0 == self.size
}
fn len(&self) -> usize {
self.size
}
// 清空栈
fn clear(&mut self) {
self.size = 0;
self.data.clear();
}
// 将数据保存在 Vec 的末尾
fn push(&mut self, val: T) {
self.data.push(val);
self.size += 1;
}
// 将栈顶减 1 后,弹出数据
fn pop(&mut self) -> Option<T> {
if 0 == self.size {
return None;
};
self.size -= 1;
self.data.pop()
}
// 返回栈顶数据引用和可变引用
fn peek(&self) -> Option<&T> {
if 0 == self.size {
return None;
}
self.data.get(self.size - 1)
}
fn peek_mut(&mut self) -> Option<&mut T> {
if 0 == self.size {
return None;
}
self.data.get_mut(self.size - 1)
}
// 以下是为栈实现的迭代功能
// into_iter: 栈改变,成为迭代器
// iter: 栈不变,得到不可变迭代器
// iter_mut:栈不变,得到可变迭代器
fn into_iter(self) -> IntoIter<T> {
// into_iter()方法获取了一个迭代器,然后进行迭代
IntoIter(self)
}
fn iter(&self) -> Iter<T> {
let mut iterator = Iter { stack: Vec::new() };
for item in self.data.iter() {
iterator.stack.push(item);
}
iterator
}
fn iter_mut(&mut self) -> IterMut<T> {
let mut iterator = IterMut { stack: Vec::new() };
for item in self.data.iter_mut() {
iterator.stack.push(item);
}
iterator
}
}
// 实现三种迭代功能
struct IntoIter<T>(Stack<T>);
// Iterator 是 Rust 的迭代器 迭代器(iterator)负责遍历序列中的每一项和决定序列何时结束的逻辑。当使用迭代器时,我们无需重新实现这些逻辑。
impl<T: Clone> Iterator for IntoIter<T> {
// into_iter()方法获取了一个迭代器,然后进行迭代。
type Item = T;
fn next(&mut self) -> Option<Self::Item> {
// 迭代器之所以成为迭代器,是因为实现了Iterator trait。要实现该特征,最主要的就是实现其中的 next 方法,该方法控制如何从集合中取值,最终返回值的类型是关联类型 Item。
if !self.0.is_empty() {
self.0.size -= 1;
self.0.data.pop()
} else {
None
}
}
}
// 'a 生命周期标识 用于帮助编译器检查引用的有效性,避免悬垂引用和使用已被释放的内存。
// 从所有权的角度来理解,就是它可以避免因为Copy或者clone的造成的不必要开销
struct Iter<'a, T: 'a> {
stack: Vec<&'a T>, // 'a 被用在了传参类型 T 上
}
impl<'a, T> Iterator for Iter<'a, T> {
type Item = &'a T; // 生命周期标识只作用于引用上,且放在&符号之后 如这里的 &'a T
fn next(&mut self) -> Option<Self::Item> {
self.stack.pop()
}
}
struct IterMut<'a, T: 'a> {
stack: Vec<&'a mut T>,
}
impl<'a, T> Iterator for IterMut<'a, T> {
type Item = &'a mut T;
fn next(&mut self) -> Option<Self::Item> {
self.stack.pop()
}
}
use std::collections::HashMap;
fn main() {
let infix = "( A + B ) * ( C + D )";
let postfix = infix_to_postfix(infix);
match postfix {
Some(val) => {
println!("{infix} -> {val}");
},
None => {
println!("{infix} is not a correct infix string");
}
}
let infix = "( 1 + 2 ) * 3";
let postfix = infix_to_postfix(infix);
match postfix {
Some(val) => {
println!("{infix} -> {val}");
},
None => {
println!("{infix} is not a correct infix string");
}
}
}
// 中缀转后缀
fn infix_to_postfix(infix:&str) -> Option<String> {
// 括号匹配检验
if !par_checker3(infix) { return None;};
// 设置各个运算符的优先级
let mut prec = HashMap::new();
// HashMap 类型储存了一个键类型 K 对应一个值类型 V 的映射。它通过一个 哈希函数(hashing function)来实现映射,决定如何将键和值放入内存中。
prec.insert("(", 1);
prec.insert(")", 1);
prec.insert("+", 2);
prec.insert("-", 2);
prec.insert("*", 3);
prec.insert("/", 3);
// ops 用于保存运算符, postfix 用于保存后缀表达式
let mut ops = Stack::new(); // 保存运算符
let mut postfix = Vec::new(); // 保存后缀表达式
for token in infix.split_whitespace() { // 按空格分割字符串切片
// 将数字 0 - 9 和 大写字母 A - Z 入栈
if ("A" <= token && token <= "Z") || ("0" <= token && token <= "9") {
postfix.push(token); // 如果是字符或数字就存入 postfix
}else if "(" == token {
// 遇到开始符号,将运算符入栈
ops.push(token); // 如果是开始括号运算符 ( 就存储 ops
}else if ")" == token {
// 比如 infix 为 (1 + 2) * 3,此时 postfix 类似为 [1,2],ops 类似为 [(,+]
// 遇到结束符号,将操作数入栈
let mut top = ops.pop().unwrap(); // 如果是结束括号运算符 就去 ops 中匹配 对应的 开始 括号运算符 此时 ops 类似为 [(],因为 + 已经被 pop 出去了
while top !="(" { // 如果匹配到的不是 ( 开始括号运算符,则说明是 + - * / 运算符 此时 top 比如为 +
postfix.push(top); // 将 + - * / 运算符入栈至 postfix,比如 infix 为 (1 + 2) * 3,此时 postfix 类似为 [1,2,+]
top = ops.pop().unwrap(); // 此时 ops 类似为 [],top = "(",到这里 while 就结束了 因为 top = "("
}
// 到这里时 ops 类似为 [],infix 为 (1 + 2) * 3 中的 () 就被丢弃了,而 postfix 已经为,如:[1,2,+]
}else {
// + - * / 运算符
// 比较运算符的优先级以决定是否将运算符添加到 postfix 列表中
while (!ops.is_empty()) && (prec[ops.peek().unwrap()] >= prec[token]) {
postfix.push(ops.pop().unwrap()); // 比如 peek 是 *,而 当前 token 是 + ,则直接把 * 放入 postfix
}
ops.push(token); // 此时将 * push 了进去
// 此时 ops 如 [*]
}
}
// 比如:infix 为 (1 + 2) * 3
// 此时 ops 如 [*]
// 此时 postfix 如 [1,2,+,3]
// 将剩下的操作数入栈
while !ops.is_empty() {
postfix.push(ops.pop().unwrap()); // 此时 postfix 如 [1,2,+,3,*]
}
// 出栈并组成字符串
let mut postfix_str = "".to_string();
for c in postfix {
postfix_str += &c.to_string();
postfix_str += " "; // 加上空格
}
Some(postfix_str)
}
// 同时检测多种开始符号和结束符号是否匹配
fn par_match(open: char, close: char) -> bool {
let opens = "([{";
let closers = ")]}";
opens.find(open) == closers.find(close)
}
// 基于栈的符号匹配
fn par_checker3(par: &str) -> bool {
let mut char_list = Vec::new();
for c in par.chars() {
char_list.push(c);
}
let mut index = 0;
let mut balance = true;
let mut stack = Stack::new();
while index < char_list.len() && balance {
let c = char_list[index];
// 将开始符号入栈
if '(' == c || '[' == c || '{' == c {
stack.push(c);
}
// 如果是结束符号,则判断是否平衡
if ')' == c || ']' == c || '}' == c {
if stack.is_empty() {
balance = false;
} else {
let top = stack.pop().unwrap();
if !par_match(top, c) {
balance = false;
}
}
}
// 非括号字符直接跳过
index += 1;
}
balance && stack.is_empty()
}
运行结果: