第三十三天| 1005.K次取反后最大化的数组和、134. 加油站 、135. 分发糖果
Leetcode 1005.K次取反后最大化的数组和
题目链接:1005 K次取反后最大化的数组和
题干:给你一个整数数组
nums和一个整数k,按以下方法修改该数组:
- 选择某个下标
i并将nums[i]替换为-nums[i]。重复这个过程恰好
k次。可以多次选择同一个下标i。以这种方式修改数组后,返回数组 可能的最大和 。
思考:两次贪心法。首先处理负数,局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。在数组全为正数且转换次数还剩的情况下,局部最优:只找数值最小的正整数进行反转,当前数值和可以达到最大,全局最优:整个 数组和 达到最大。
本题的解题步骤为:
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时K--
- 第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
- 第四步:求和
代码:
class Solution {
public:
static int cmp(int a, int b) { //按绝对值比较
return abs(a) > abs(b);
}
int largestSumAfterKNegations(vector& nums, int k) {
sort(nums.begin(), nums.end(), cmp); //排序
int count = k;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] < 0 && count > 0) { //转换次数够的情况下负数取反
nums[i] *= -1;
count--;
}
}
if (count % 2 == 1) //剩余次数为奇数转换绝对值最小的正数
nums[nums.size() - 1] *= -1;
int result = 0;
for (int m : nums)
result += m;
return result;
}
}; Leetcode 134. 加油站
题目链接:134 加油站
题干:在一条环路上有
n个加油站,其中第i个加油站有汽油gas[i]升。你有一辆油箱容量无限的的汽车,从第
i个加油站开往第i+1个加油站需要消耗汽油cost[i]升。你从其中的一个加油站出发,开始时油箱为空。给定两个整数数组
gas和cost,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回-1。如果存在解,则 保证 它是 唯一 的。
思考一:暴力法。遍历每一个加油站为起点的情况,模拟一圈。如果跑了一圈,中途没有断油,而且最后油量大于等于0,说明这个起点是ok的。(超时)
代码:
class Solution {
public:
int canCompleteCircuit(vector& gas, vector& cost) {
for (int i = 0; i < gas.size(); i++) {
int remainder = gas[i] - cost[i]; //到达下一站的剩余油量
int index = (i + 1) % gas.size(); //到达的下一站
while (remainder > 0 && index != i) { //寻找能到达的最远站(remainder等于0无法保证答案唯一)
remainder += gas[index] - cost[index];
index = (index + 1) % gas.size();
}
if (remainder >= 0 && index == i) return i; //以i为起点跑了一圈
}
return -1;
}
}; 思考二:贪心法。如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量remainder[i]相加一定是大于等于零的。那么让i从0开始累加remainder[i],和记为curRemainder,一旦curRemainder小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curRemainder。
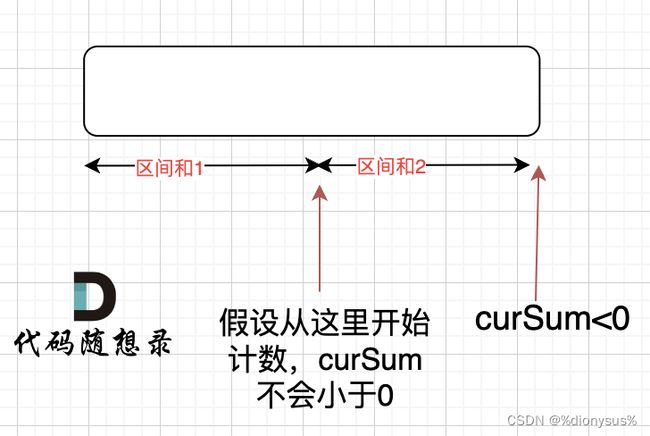
- 这里可能存在一个疑惑:为什么curRemainder小于零起始位置就从i+1算起,而不是从[0, i]中间节点算起。
如果 curRemainder<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curRemainder不会小于0的话,就是 区间和2>0。区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。
当然遍历过程要统计总加油量和耗油量,如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的。
代码:
class Solution {
public:
int canCompleteCircuit(vector& gas, vector& cost) {
int curRemnant = 0; //记录当前剩余油量
int totalRemnant = 0; //记录转一圈后剩余油量
int start = 0; //记录出发点
for (int i = 0; i < gas.size(); i++) {
curRemnant += gas[i] - cost[i];
totalRemnant += gas[i] - cost[i];
if (curRemnant < 0) { //start为起始节点失败
curRemnant = 0;
start = i + 1;
}
}
if (totalRemnant < 0) return -1; //跑完一圈累计油量为负则无法跑完
return start;
}
}; 思考三:直接从全局进行贪心选择,情况如下:
-
情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
-
情况二:gas[i]-cost[i]为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
-
情况三:如果累加的最小值是负数,汽车就要从非0节点出发,从后向前,看哪个节点能把这个负数填平,能把这个负数填平的节点就是出发节点。
代码:
class Solution {
public:
int canCompleteCircuit(vector& gas, vector& cost) {
int remainder = 0;
int min = INT_MAX; //记录最小累计加油量与累计油耗的差
for (int i = 0; i < gas.size(); i++) {
remainder += gas[i] - cost[i];
if (remainder < min)
min = remainder;
}
if (remainder < 0) return -1; //总油耗大于总加油量
if (min >= 0) return 0; //0作为起始点经过中间站不存在油量不足的情况
for (int i = gas.size() - 1; i > 0; i--) { //从后往前寻找弥补最小差
min += gas[i] - cost[i];
if (min >= 0)
return i;
}
return -1;
}
}; Leetcode 135. 分发糖果
题目链接:135 分发糖果
题干:
n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。- 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
思考:贪心法。此题同时考虑左右两边情况较难处理。因此将确定一边之后,再确定另一边。
- 先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
- 再确定左孩子大于右孩子的情况(从后向前遍历)
此时局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
代码:
class Solution {
public:
int candy(vector& ratings) {
vector vec(ratings.size(), 1);
//从前往后 确定右孩子大于左孩子的情况
for (int i = 1; i < ratings.size(); i++) {
if (ratings[i] > ratings[i - 1])
vec[i] = vec[i - 1] + 1;
}
//从后往前 确定左孩子大于右孩子的情况
for (int i = ratings.size() - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1])
vec[i] = max(vec[i], vec[i + 1] + 1);
}
int result = 0;
for (int m : vec) //统计糖果数目
result += m;
return result;
}
}; 自我总结:
- 贪心法考虑分步处理以及合并思考