基于 Python 和 cvxpy 求解 SOCP 二阶锥规划问题
cvxpy: Python 功能包,为凸优化提供方便使用的用户接口,适配多种求解器
SOCP: Second-Order Cone Programming,二阶锥规划
convex optimization - 凸优化,nonlinear optimization - 非线性优化
time complexity - 时间复杂度,polynomial-time - 多项式时间
Euclidean norm - 欧几里德范数
文章目录
- 什么是 SOCP 二阶锥规划
-
- 与其他优化问题的关系
- 如何使用 cvxpy 求解 SOCP
-
- 求解案例
- 指定求解器
什么是 SOCP 二阶锥规划
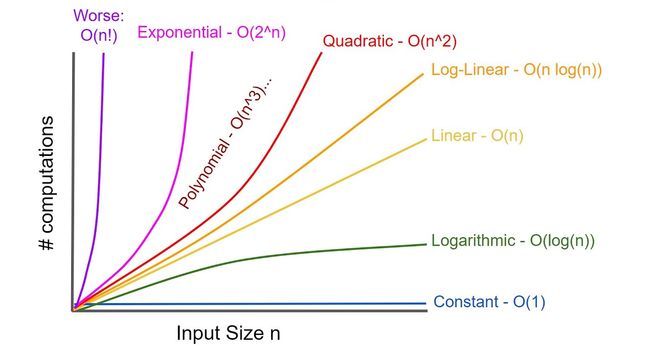
二阶锥规划是一种凸优化问题。不同于非线性优化,多数凸优化问题求解方法的时间复杂度是多项式时间的,即运算时长与输入维度呈多项式关系。由于非线性优化一般是 NP-hard 问题,目前对于 NP-hard 问题没有多项式时间的求解方法。
下图为各种时间复杂度的对比。
minimize f ⊤ x s.t. ∥ A i x + b i ∥ 2 ≤ c i ⊤ x + d i , i = 1 , … , m F x = g , \begin{aligned} \text{minimize} \; \; \; \; &f^\top x \\ \text{s.t.} \;\;\;\; &\| A_i x + b_i \|_2 \le c_i^\top x + d_i, \;\;\; i = 1, \dots, m \\ &Fx = g, \end{aligned} minimizes.t.f⊤x∥Aix+bi∥2≤ci⊤x+di,i=1,…,mFx=g,
目标函数中 x x x 是 n n n 维列向量表示待优化变量, f f f 是 n n n 维列向量, f ⊤ x f^\top x f⊤x 是一维的目标函数值;
A i A_i Ai 是 n i × n n_i \times n ni×n 维矩阵, b i b_i bi 是 n i n_i ni 维列向量, c i c_i ci 是 n n n 维列向量, d i d_i di 是一维标量, F F F 是 p × n p \times n p×n 维矩阵, g g g 是 p p p 维列向量;
f , A i , b i , c i , d i , F , g f, A_i, b_i, c_i, d_i, F, g f,Ai,bi,ci,di,F,g 都是优化问题的参数,该优化问题有 m m m 个二阶锥约束和 p p p 个等式约束;
∥ ∥ 2 \| \|_2 ∥∥2 表示欧几里德范数,即距离范数。
与其他优化问题的关系
二阶锥规划与其他优化问题的关系详见下图。
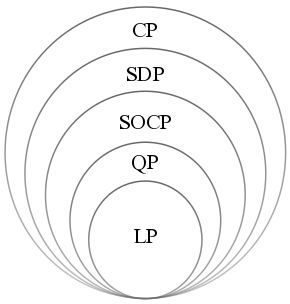
LP: Linear Programming,线性规划;QP: Quadratic Programming,二次规划;SOCP: Second-Order Cone Programming,二阶锥规划;SDP: Semidefinite Programming,半正定规划;CP: Conic Optimization,锥规划。
图中的问题是包含关系,例如 LP 是 QP 的特殊形式,QP 相比 LP 更一般(general)。
如何使用 cvxpy 求解 SOCP
求解案例
下面的例子求解了一个随机生成的二阶锥规划问题,由于指定了随机种子 np.random.seed(2),其多次运行的结果是一致的。例子中向量、矩阵与维度定义所用的符号(例如 f , A i , b i , c i , d i , F , g f, A_i, b_i, c_i, d_i, F, g f,Ai,bi,ci,di,F,g 等)与上文的数学表达一一对应。
# 导入功能包
import cvxpy as cp
import numpy as np
# 生成一个随机且可行的 二阶锥规划问题
# 维度定义
m = 3
n = 10
p = 5
n_i = 5
np.random.seed(2) # 指定随机种子
# 向量与矩阵定义
f = np.random.randn(n)
A = []
b = []
c = []
d = []
x0 = np.random.randn(n)
# 赋值每一个 A_i, b_i, c_i, d_i
for i in range(m):
A.append(np.random.randn(n_i, n))
b.append(np.random.randn(n_i))
c.append(np.random.randn(n))
d.append(np.linalg.norm(A[i] @ x0 + b, 2) - c[i].T @ x0)
F = np.random.randn(p, n)
g = F @ x0
# 在 CVXPY 中定义并求解该问题
x = cp.Variable(n)
# cp.SOC(t, x) 用于设置二阶锥约束 ||x||_2 <= t.
soc_constraints = [
cp.SOC(c[i].T @ x + d[i], A[i] @ x + b[i]) for i in range(m)
]
prob = cp.Problem(cp.Minimize(f.T@x),
soc_constraints + [F @ x == g])
prob.solve() # 求解
# 输出结果
print("The optimal value is", prob.value)
print("A solution x is")
print(x.value)
for i in range(m):
print("SOC constraint %i dual variable solution" % i)
print(soc_constraints[i].dual_value)
输出如下。
The optimal value is -9.582695716265503
A solution x is
[ 1.40303325 2.4194569 1.69146656 -0.26922215 1.30825472 -0.70834842
0.19313706 1.64153496 0.47698583 0.66581033]
SOC constraint 0 dual variable solution
[ 0.61662526 0.35370661 -0.02327185 0.04253095 0.06243588 0.49886837]
SOC constraint 1 dual variable solution
[ 0.35283078 -0.14301082 0.16539699 -0.22027817 0.15440264 0.06571645]
SOC constraint 2 dual variable solution
[ 0.86510445 -0.114638 -0.449291 0.37810251 -0.6144058 -0.11377797]
指定求解器
求解时 prob.solve() 可以指定求解器。以下两个求解器(SCS 和 ECOS)是与 CVXPY 一同安装且支持二阶锥规划问题的。在有些问题上,SCS 求解速度更快 link,决定使用哪个求解器需要具体问题具体分析,不仅关系到求解速度,还和求解器自身的各项设置有关 link(例如 ECOS 的默认精度高于 SCS)。
prob.solve(solver=cp.SCS)
prob.solve(solver=cp.ECOS)
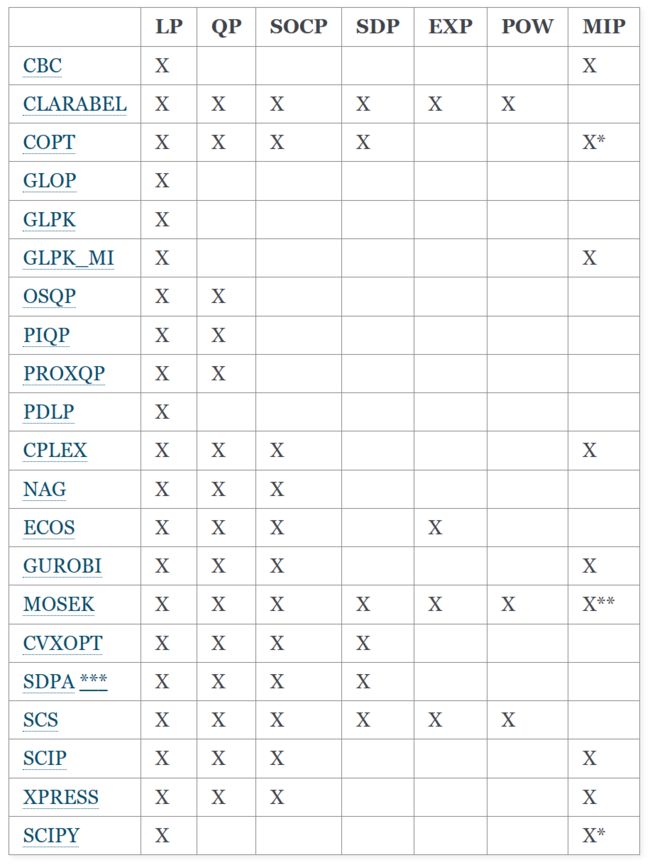
很多其他的求解器也可以求解二阶锥规划问题,不过需要单独安装,见下表 link。