leetcode算法总结(基于carl网站)
前言
本篇参考链接: 代码随想录.
所有类型题都可在网站里找到,这里不做详细标注
数组
二分查找
-
适用情况:在已经排序好的数组(元素无重复)中快速找到某一个满足条件的元素。
-
例题:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 -
思考
- 用哈希会怎么样?
在已经排序好的数组下,用哈希耗时更长,若是未排序好的数组可以考虑用哈希。
- 用哈希会怎么样?
双指针法
填充数组模拟过程
链表
小tips
设置虚拟头节点 做题有奇效!
双指针法
适用情况:
- 单个链表:
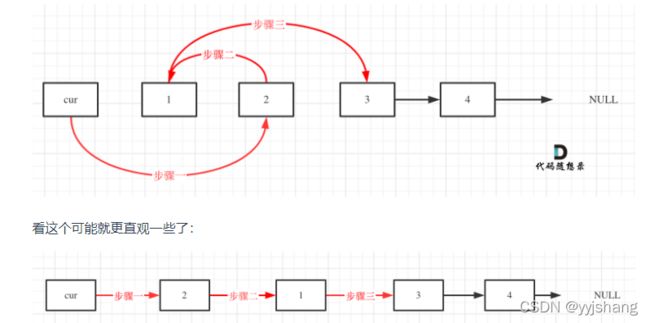
反转链表(慢指针指向虚拟头节点,快指针指向下一个节点)、删除倒数第n个元素(慢快指针指向虚拟、快指针先移动n+1)、判断链表是否有环、环的入口在哪(慢指针走一步快指针走两步,若慢指针与快指针相遇说明有环(但最终相遇的点不一定是环的入口,可能过程中就相遇了)) - 两个链表
找两个链表是否存在交点(注意交点之后一直是重合的)(首先找出长度差,长的链表指针移动到与短链表重合)
模拟链表交换
脑图
哈希表
适用情况:快速判断一个元素是否出现集合就要考虑哈希法。
字符串
综合题型:151. 颠倒字符串中的单词.
双指针法
适用情况:反转字符串(一个指针指向首部、另一个指针指向尾部,for循环一次两者向中间移动直至相遇)、修改(填充或删除)字符串(考虑扩容、双指针指向)。
KMP算法
适用情况:查找一个串是否出现在另一个串
二叉树
二叉树相关算法总结.
回溯
适用情况:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
模板
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
常用解题思路
组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
- for中i从startIndex开始。
class Solution {
private:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果
void backtracking(int n, int k, int startIndex) {
if (path.size() == k) {
result.push_back(path);
return;
}
for (int i = startIndex; i <= n; i++) {
path.push_back(i); // 处理节点
backtracking(n, k, i + 1); // 递归
path.pop_back(); // 回溯,撤销处理的节点
}
}
public:
vector<vector<int>> combine(int n, int k) {
result.clear(); // 可以不写
path.clear(); // 可以不写
backtracking(n, k, 1);
return result;
}
};
排列
46.全排列
-
for中 i从0开始(单个集合),有可能从startIndex开始(多个集合) ,看集合数量
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素了
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
- 组合中,for 中i 从0 还是 从startIndex
我举过例子,如果是一个集合来求组合的话,就需要startIndex,例如:回溯算法:求组合问题! (opens new window),回溯算法:求组合总和! (opens new window)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:回溯算法:电话号码的字母组合
同层不允许使用和同树枝允许使用
40.组合总和II
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
if (sum == target) {
result.push_back(path);
return;
}
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = true;
backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次
used[i] = false;
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(), false);
path.clear();
result.clear();
// 首先把给candidates排序,让其相同的元素都挨在一起。
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0, used);
return result;
}
};
同层不允许使用
491.递增子序列
// 版本一
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
if (path.size() > 1) {
result.push_back(path);
// 注意这里不要加return,要取树上的节点
}
unordered_set<int> uset; // 使用set对本层元素进行去重
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back())
|| uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> findSubsequences(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
回溯难题
N皇后.
棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了。
class Solution {
private:
vector<vector<string>> result;
// n 为输入的棋盘大小
// row 是当前递归到棋盘的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
result.clear();
std::vector<std::string> chessboard(n, std::string(n, '.'));
backtracking(n, 0, chessboard);
return result;
}
};
解数独.
class Solution {
private:
bool backtracking(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board)) {
board[i][j] = k; // 放置k
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; // 回溯,撤销k
}
}
return false; // 9个数都试完了,都不行,那么就返回false
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};
动态规划
思路
推出状态方程,把每步状态方程打印出来验证。
简单题目
第一步 确定dp【i】的含义
第二步 确定推导方程
第三部 确定dp【0】或dp【1】的初始化
爬楼梯
leetcode 70. 爬楼梯.
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
背包问题题目
- 例题:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
- 解析:其中
if (j < weight[i]) dp[i][j] = dp[i - 1][j];所以 if 和else 可以合并成另一个推导式:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);转换为一维数组可以是dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
那么可以写成(注意是倒叙遍历背包容量,否则会造成一个物品被连续放入)
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
巧妙运用背包问题帮助解题
背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。
01背包
多个物品,一个物品只能放一次
- 即是价值也是重量
- 核心代码
只能先遍历物品 后遍历背包(逆序遍历是为了防止物品**重复放入**!)
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
递推式//dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
- 问题类似描述:
-
存在两个相等值。区分出两个相等值。两个值可以相互抵消。 例题:1049 ,416 。
-
存在关系公式 ,转换概念:加起来等于某一个值有几种方法? ——>>>> 装满背包有几种方法?例题:494.目标和
-
两个维度的01背包
两个物品(重量等于价值)分别放入两个01背包 494.目标和
完全背包
多个物品,一个物品可以放入多次
- 核心代码
在一些题目中如( 518. 零钱兑换 II )
先遍历物品,再遍历背包 算的是组合数518. 零钱兑换 II, 先遍历背包后遍历物品算的是排列数377. 组合总和 Ⅳ。
但通常两种遍历顺序都是可以的,根据题意判断!。
要点注意
- for循环语句中的condition 即
i < weight.size()要注意与 for循环内用if语句的 区别!输出结果是不同的!
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
- 关于字符串匹配的完全背包
两种方式解题 截取源字符串对比 字符串数组,反过来用字符串数组元素 与 源字符串进行对比。 一般用前者 去套入完全背包,如例题 139. 单词拆分
注意背包问题一维dp数组初始化方式
- 一维dp数组
- 题目要求返回xxx最小数量,dp推导数组就应该是
dp[i] = min(dp.., dp..)那么初始化应该为vector,初始化为最大值。反之,可以依据题目设为 -1 或 0dp(bagSize + 1, INT_MAX)
例题:322. 零钱兑换、279. 完全平方数
- 二维dp数组
vector就是没有加1。dp(bagSize , INT_MAX)
注意for循环范围、与元素首末下标参数的表达是否在同一维度
337. 打家劫舍 II 如该题的 start 、end 和 i的维度关系。
树形DP
337. 打家劫舍 III
动态规划状态分析
买卖股票系列
- 最佳买卖股票时机含冷冻期
-
达到买入股票状态(状态一)即:dp[i][0],有两个具体操作:
操作一:前一天就是持有股票状态(状态一),dp[i][0] = dp[i - 1][0]
操作二:今天买入了,有两种情况
前一天是冷冻期(状态四),dp[i - 1][3] - prices[i]
前一天是保持卖出股票状态(状态二),dp[i - 1][1] - prices[i]
所以操作二取最大值,即:max(dp[i - 1][3], dp[i - 1][1]) - prices[i]
那么dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]); -
达到保持卖出股票状态(状态二)即:dp[i][1],有两个具体操作:
操作一:前一天就是状态二
操作二:前一天是冷冻期(状态四)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]); -
达到今天就卖出股票状态(状态三),即:dp[i][2] ,只有一个操作:
操作一:昨天一定是买入股票状态(状态一),今天卖出
即:dp[i][2] = dp[i - 1][0] + prices[i]; -
达到冷冻期状态(状态四),即:dp[i][3],只有一个操作:
操作一:昨天卖出了股票(状态三)
dp[i][3] = dp[i - 1][2];
注意要点
- 多注意导致冷冻期的这一动作的状态分析
- 运用标志位在for循环判断冷冻期,会导致不是最优解,应多分析几种状态。状态不能有重合
找到最长符合条件的序列
- 非连续递增/递减/相同/序列
- 最长严格递增子序列. 一个判断数组
- dp[i]:以nums【i】结尾的最长递增序列。
- 最长公共子序列 . 两个判断数组
- dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
- 不相交的线 . 两个判断数组
直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
- 最长严格递增子序列. 一个判断数组
- 连续递增/递减/相同序列
- 最长连续递增序列. 一个判断数组
- dp[i] 以nums【i】结尾的最长连续递增序列。
- 最长重复子数组.两个判断数组
- dp[i] 以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]
- 最长连续递增序列. 一个判断数组
考虑序列类型题目dp含义的几种思路
单个判断数组:只考虑首点,只考虑尾点,考虑首尾点。
两个判断数组:dp[i][j]表示考虑以下标 i - 1结尾的nums1 和 以下标 j - 1 结尾的nums2最长重复序列(符合条件的结果)
贪心算法
- 121. 买卖股票的最佳时机
注意题意只买一次也只卖一次,可运用贪心也可以运用动态规划。
没有规律可言,就是贪!你要最大我就先挑最大!局部最优推出全局最优
图论算法
基础算法
最短路径算法:Floyd,Dijkstra(必学)
最小生成树算法:Prim,Kruskal(必学)
遍历算法:深度搜索和广度搜索(必学)
遍历找某点到任意点的最短距离模板(上下左右版)
思路
- 建立
mp[N][M]图 - 记忆经过的点
book[N][M] - 建立结构体(点、点、符合题意的值 )
如:struct Point { int x,y,t;//点,点 ,离起点的最短距离 }b[10]; - bfs 广度优先遍历 用queue容器迭代
- 遍历图,找最短距离,用队列
queue迭代(广度优先)
ps:为什么不用栈? 因为栈的先进后出的原则,适用于深度优先。
示例代码:
只能上下左右走,确定到每个点的最短距离。
bool book[N][N];//记录经过的点
struct Point
{
int x,y,t;//点,点 ,离起点的最短距离
}b[10];
//四个方向,方便模拟
int xM[4] = {0,1,0,-1};
int yM[4] = {1,0,-1,0};
int dp[x][y][1];//1号宝箱(tx,ty)到每个点的最短距离
//在m*n的图中 找1号宝箱到每个点的最短距离
int bfs(int tx,int ty) {
memset(book,0,sizeof(book));
Point root;
queue<Box> st;
root.x = x;
root.y = y;
root.t = 0;
st.push(root);
book[x][y] = true;
while(!st.empty()) {
Box w = st.front();
st.pop();
for(int i = 0; i < 4; i++)
{
int xx = w.x + xM[i];
int yy = w.y + yM[i];
int temp = w.t+1;
if(xx == tx && yy == ty) return temp;
if(xx >= 0 && xx < m && yy >= 0 && yy < n && !book[xx][yy] && mp[xx][yy] != '#')
{
book[w.x][w.y] = true;
dp[x][y][1] = temp;
st.push(Box{xx,yy,temp});
}
}
}
return -1;
}
例题:
网易真题-迷宫寻宝-研发
#include Dijikstra算法
详解
一个for 初始化dis, while贪心起点到每个点的最短距离
void Graph_DG::Dijkstra(int begin){
//首先初始化我们的dis数组
int i;
for (i = 0; i < this->vexnum; i++) {
//设置当前的路径
dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);
dis[i].value = arc[begin - 1][i];
}
//设置起点的到起点的路径为0
dis[begin - 1].value = 0;
dis[begin - 1].visit = true;
int count = 1;
//计算剩余的顶点的最短路径(剩余this->vexnum-1个顶点)
while (count != this->vexnum) {
//temp用于保存当前dis数组中最小的那个下标
//min记录的当前的最小值
int temp=0;
int min = INT_MAX;
for (i = 0; i < this->vexnum; i++) {
if (!dis[i].visit && dis[i].value < min) {
min = dis[i].value;
temp = i;
}
}
//cout << temp + 1 << " "<
//把temp对应的顶点加入到已经找到的最短路径的集合中
dis[temp].visit = true;
++count;
for (i = 0; i < this->vexnum; i++) {
//注意这里的条件arc[temp][i]!=INT_MAX必须加,不然会出现溢出,从而造成程序异常
if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
//如果新得到的边可以影响其他为访问的顶点,那就就更新它的最短路径和长度
dis[i].value = dis[temp].value + arc[temp][i];
dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);
}
}
}
}
Floyd
模板1
核心思想:这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。
1 for(k=1;k<=n;k++)
2 for(i=1;i<=n;i++)
3 for(j=1;j<=n;j++)
4 if(e[i][j]>e[i][k]+e[k][j])
5 e[i][j]=e[i][k]+e[k][j];
模板2
一定边数内的最短距离
for(int t = 1; t < k+2; t++){ //遍历边
for(auto flight:flights){ //遍历两点距离
int i = flight[0];//点A
int j = flight[1];//点B
int dis = flight[2];//A-》B的距离
//松弛
dp[t][j] = min(dp[t][j],dp[t-1][i] + dis);//表示从起点经过 t 条边到 j 点的距离
if(j == dst) res = min(res,dp[t][j]);
}
}
- leetcode787. K 站中转内最便宜的航班
dp【t】【j】表示从起点经过 t 条边到 j 点的距离
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
vector<vector<int>> dp(k+2,vector<int>(n,INT_MAX/2));
int res = INT_MAX/2;
dp[0][src]=0;
for(int t = 1; t < k+2; t++){ //遍历边
for(auto flight:flights){ //遍历两点距离
int i = flight[0];
int j = flight[1];
int dis = flight[2];
//松弛
dp[t][j] = min(dp[t][j],dp[t-1][i] + dis);
if(j == dst) res = min(res,dp[t][j]);
}
}
return res == INT_MAX/2? -1:res;
}
};
并查集
参考:很有意思的并查集讲解
简单易懂的例题模板套用
思路
- 写出并查集通用函数
find - 自立为王(初始化find【】数组)
- 遍历边,不连通则连起来
#include